Урок в 11 классе по теме

«Касательная к графику функции».

Образовательное учреждение: МБОУ СОШ №2 город Батайск.

Дата: 08.10.2013 г.

Предмет: математика.

Класс: 11 «Б».

УМК: «Алгебра и начала математического анализа. 11 класс».

Авторы УМК: Г. К. Муравин - кандидат педагогических наук, О.В. Муравина - кандидат педагогических наук, доцент, заведующая редакцией математики и информатики издательства «Дрофа».

Учитель: Логинова Т. Э. учитель - экспериментатор, учитель математики высшей категории МБОУ СОШ №2 города Батайска.

Научное консультирование: Зевина Л.В - научный руководитель областных экспериментальных и пилотных площадок по апробации УМК в школах Ростовской области, Master of education, кандидат педагогических наук, доцент, заведующая кафедрой математики и естественных дисциплин ГБОУ ДПО РО РИПК и ППРО.

Тема урока: «Касательная к графику функции».

Тип урока: урок изучения нового материала.

Оборудование: УМК «Алгебра и начала математического анализа. 11 класс» автор Г. К. Муравин, О.В. Муравина, интерактивная доска, карточки обратной связи.

Цели урока: организация продуктивной деятельности школьников, направленной на достижение ими следующих результатов:

• Предметных:

- понимание смысла «касательная к графику функции»;

- осознанное употребление нового математического понятия в устной и письменной речи;

- овладение опытом построения касательной к графику функции в простых случаях, опираясь на использование уже имеющихся знаний;

- приобретение способности «открывать» новое математическое знание;

-понимание сути и осознанное использование математических средства наглядности (рисунки и чертежи) для иллюстрации и аргументации собственных рассуждений и действий;

- умение формулировать учебную тему и учебные задачи, используя математическую терминологию.

• Метапредметных:

Освоение способов деятельности:

- познавательной:

- сравнение, сопоставление, классификация, ранжирование объектов по одному или нескольким признакам

- комбинирование известных алгоритмов деятельности в ситуациях, не предполагающих стандартного применения одного из них;

- исследование несложных практических ситуаций, выдвижение предположений, понимание необходимости их проверки на практике;

- умение мотивированно отказаться от образца, искать оригинальное решение;

- умение разделять процессы на этапы и звенья;

- использование различных методов (опыт, наблюдение);

- информационно - коммуникативной:

- умение вступать в речевое общение, участвовать в диалоге;

- отражение в устной и письменной форме результатов своей деятельности;

- умение перефразировать мысль, анализировать, аргументировать сделанный вывод;

- проведение информационно - смыслового анализа задания;

- приведение примеров, подбор аргументов, формулирование выводов.

- рефлексивной:

- фиксация затруднения и поиск причин возникших трудностей и их устранение;

- оценивание своих учебных достижений;

- умение работать в парах и индивидуально;

- умение ставить личностные цели и оценивать степень их достижения.

Личностных:

1) стимулировать способность иметь собственное мнение;

2) умение легко выполнять математические операции;

3) умение точно и грамотно излагать свои мысли;

4) умение контролировать процесс и результат учебной математической деятельности;

5) умение хорошо говорить и легко выражать свои мысли.

Лучший способ изучить что либо - это открыть самому.

Дьёрдь Пойа

Ход урока:

1. Организационно-мотивационный этап.

- Здравствуйте, ребята! За окном золотая осень! Я уверена, что сегодня на уроке всем будет комфортно, отношения будут тёплые. Не бойтесь сделать ошибку! Ошибка - источник Вашего личного опыта.

- Разрешите Вам представить наших гостей.

Зевина Любовь Васильевна - кандидат педагогических наук, доцент, заведующая кафедрой математики и естественных наук РИПК и ППРО, научный руководитель областных экспериментальных и пилотных площадок по апробации УМК авторов Муравина Г.К. и Муравиной О.В. в школах Ростовской области.

Учителя математики нашего города и других районов и городов Ростовской области.

На нашем уроке присутствует директор школы Покровская Наталья Владимировна.

(учитель представляет присутствующих гостей).

- Выдающийся венгерский, швейцарский и американский математик утверждал: «Лучший

способ изучить что- либо - это открыть самому».

2. Этап постановки личностных целей.

- На экране Вы видите список личностных целей.

Личностные цели:

1) приобрести способность иметь собственное мнение;

2) умение легко выполнять математические операции;

3) подготовиться к успешной сдаче ЕГЭ;

4) умение точно и грамотно излагать свои мысли;

5) научиться ничего не принимать на веру;

6) умение контролировать процесс и результат учебной математической деятельности;

7) получить хорошую оценку;

8) умение хорошо говорить и легко выражать свои мысли.

- Выберите из этого списка для себя цель. Напишите на полях в тетради ее номер. Постарайтесь поработать на неё в течение всего урока. В конце урока мы проанализируем, достигли вы её или нет и почему.

- Сегодня на уроке Вы сами себя будете оценивать. За каждый правильный ответ, за выход к доске на полях тетрадки ставьте балл, в конце урока посчитаете количество баллов и поставите себе оценку:

«7 баллов и более» - 5;

«4-6 баллов» - 4;

«1 -3 балла» -3;

«0 баллов» - 2.

Обратная связь на уроке осуществляется при помощи сигнальных карточек красного и зеленого цветов. Приготовьте свои сигнальные карточки. На каждый прозвучавший ответ вы поднимаете сигнальные карточки, показывая зелёным цветом, что у вас такое же мнение. В случае расхождения мнений вы показываете красную карточку, идёт обсуждение, выявляется причина разногласия.

Прочитайте число 8102013 поставьте точки после ед. миллионов и десятков тысяч. Что получилось, на что похоже 8.10.2013?

Откройте тетради и запишите число, классная работа.

3. Этап актуализации знаний.

- Ребята, посмотрите на обложку своего учебника, ещё раз прочитайте название «Алгебра и начала анализа». Сегодня мы начинаем работать с началом математического анализа. В ходе урока Вы поймёте, что это такое, а сейчас поработаем устно.

На доске демонстрируются объекты.

Задание 1.

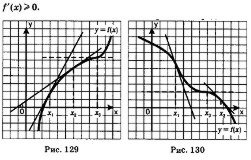
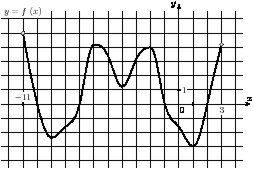
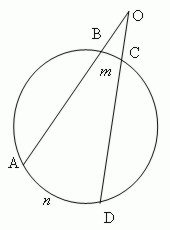
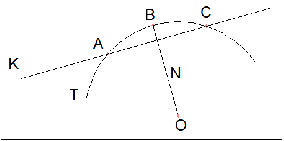
Как можно назвать объекты, которые Вы видите на экране?

Предполагаемые ответы: футбольный матч, прямая, окружность, графики функций, секущая, касательная, треугольник и т.д.

4

«Нам неба на двоих становится все мало…

И запах уст хмельных - касательная в синь

Мне жизнь здесь без тебя невыносима стала,

Пусть суетливо догорает мой камин».

(«Неизвестный гений», автор Людмила Довгуша,

социальная сеть для творческих людей)

Задание 2. Логические поисковые задания (группировка).

Разбейте эти объекты на группы, как можно большим количеством способов.

Дети предлагают свои способы разбиения (учитель записывает номера объектов по группам), указывая признак, использованный при выполнении этого задания.

Предполагаемые ответы учеников:

1 группа - геометрические фигуры,

2 группа - касание мяча на футболе,

3 группа - касание в жизни,

4 группа - касательная к окружности,

5группа - касательная к графику функции.

4. Постановка темы и цели урока:

4.1. Задание 3.

Подумайте, что общее на всех рисунках?

Предполагаемый ответ: точки касания, общая точка (выяснить: точка касания и общая точка - это одно и то же?)

4.2. Работа с текстами из словарей:

-Ребята, посмотрите на слайды и подумайте, какое одно и то же слово пропущено.

• Современный энциклопедический словарь:

……… (от латинского …… - исполнение, осуществление),

1) деятельность, обязанность, работа; внешнее проявление свойств какого-либо объекта в данной системе отношений (например, ….. органов чувств, …… денег).

2)………в социологии - роль, которую выполняет определенный социальный институт или процесс по отношению к целому (например, …… государства, семьи и т. д. в обществе).

3) …….. в математике - соответствие между переменными величинами, в силу которого каждому значению одной величины x (независимого переменного, аргумента) соответствует определенное значение другой величины y (зависимого переменного, …….). ……… могут быть заданы, например, формулой, графиком, таблицей, правилом.

• Новейший философский словарь:

……… (лат. ………. - совершение, исполнение)

1) деятельность, роль объекта в рамках некоторой системы, которой он принадлежит;

2) вид связи между объектами, когда изменение одного из них влечет изменение другого, при этом второй объект также называется ……… первого.

Возможный вариант ответа: пропущено слово-функция.

- Ребята, а теперь предположите, как будет звучать тема сегодняшнего урока?

Варианты ответов детей: «Точки касания», «Касательная», «Касательная и функция», «Касательная к графику функции» и др.

Учитель уточняет тему.

- Тема урока: «Касательная к графику функции».

( Записывают тему урока: дети - в тетради, а учитель - на доске.)

5. Фронтальная работа

5.1. Выполните письменно задания (два человека работают у доски на крыльях). Задание №1.

Задайте формулой функцию, график которой параллелен прямой

у= 2х-3 (вариант 1) у= -5х+2 (вариант 2)

и проходит через точку

(-5; 2) (вариант1) (-8; 3) (вариант 2)

(Самопроверка с выставлением баллов на полях, работа с карточками обратной связи).

Ребята, обобщите полученные результаты двух вариантов и сделайте вывод.

Примечание ( для учителей)

Пронаблюдайте: учитель не спрашивает учеников (например, о том, что является графиком функции y = kx+b); дети могут самостоятельно затронуть этот и другие теоретические вопросы и воспользоваться теорией к месту по ситуации. Учитель организует свободную учебную деятельность учащихся.

Задание №2.

В тетрадках начертите примерное расположение графика (или эскиз графика) функции

y = kx+b, если:

1) k>0 , b>0;

2) k=0 , b>0;

3) k<0, b=0 .

(Два ученика работают за доской, остальные - в тетрадках, проверяют взаимопроверкой, сигнализируя карточками обратной связи, а работающие у доски, объясняют решение ).

Примечания (для учителей)

• Поймите смысл: Муравин Георгий Константинович категорически против такой формы организации работы: один у доски, а остальные «списывают». Он ратует за работу (скрыто) на крыльях двух ребят, а остальные в это время работают у себя в тетрадях. Потом следует проверка с аргументацией одного из учеников и работа с карточками обратной связи.

• Пронаблюдайте: в процессе аргументации своих действий школьники вынуждены будут обращаться к теории, не отвечая на вопросы учителя, а размышляя самостоятельно над возникающими в процессе аргументации вопросами:

- Что обозначает b, k?

- Через какую координатную четверть при в=0, проходит график линейной функции, если коэффициент положительный, отрицательный, равен нулю?

- Какой знак имеет угловой коэффициент, если функция возрастает, убывает, параллельна оси абсцисс?

- Чему равен тангенс острого угла прямоугольного треугольника?

- Зная определение тангенса, что можно сказать об угловом коэффициенте?

6. Этап «открытия» нового знания.

Примечания (для учителей)

• Пронаблюдайте и ответьте на вопрос: в чем отличие этапа традиционного изучения нового материала и этапа «открытия» нового знания?

• Поразмышляйте: чем отличаются по смыслу процессы обучения и познания.

Учитель:

-Предлагаю выполнить несколько заданий, в которых каждому из вас можно будет проявить наблюдательность и показать умение использовать имеющиеся знания в новой ситуации.

Ситуация 1

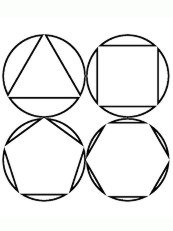
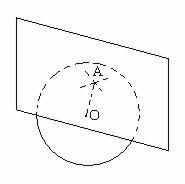
Опишите, используя математический язык и все имеющиеся у вас знания, все то, что Вы видите на рисунках 23, 24 учебника (смотри приложение).

Варианты ответов:

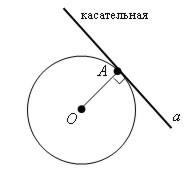
- Полуокружность имеет с прямой одну общую точку.

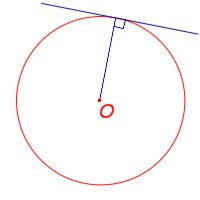
- Касательные к окружности. (Здесь возможны разногласия. Может возникнуть вопрос: Можно ли назвать эти прямые касательными? (Возможный ответ учеников: нет, поскольку не выполняется условие перпендикулярности к радиусу окружности) . Еще один вопрос для обсуждения: общая точка и точка касания - это одно и то же понятие?

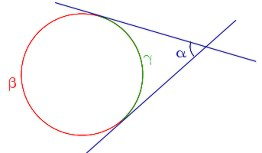
Ситуация 2

- Посмотрите на два рисунка, что Вы видите общее, а в чём различие?

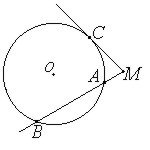
Ситуация 3

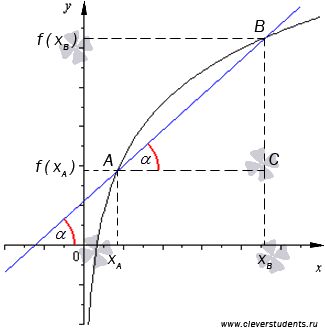
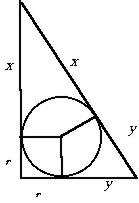
- Посмотрите на рисунок и опишите (и найдите) все, что можете, используя имеющиеся знания.

В процессе работы учащиеся смогут определить секущую; подобные прямоугольные треугольники; прямоугольники; параллельные и перпендикулярные отрезки; определить величину угла альфа и др.

Если они будут зантрудняться, учитель задаст вопросы:

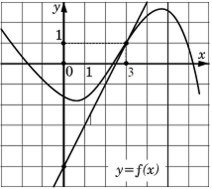
- Как называется прямая АВ? Через сколько точек она проходит?

- Назовите прямоугольный треугольник.

- Что обозначает угол альфа? Как его найти?

(Прямую AB, проведенную через две точки графика функции y=f(x), называют секущей. Другими словами, секущая - это прямая, проходящая через две точки графика функции.)

Ситуация 4

Ребята, внимательно посмотрите на рисунки, где синим цветом изображена прямая y = x+1, черным цветом - график функции ,а красным - точка (1;2). Что Вы заметили?

Варианты ответов учащихся:

-Каждый последующий рисунок является увеличенной областью предыдущего (эти области выделены красными квадратами).

- Прямая y = x+1 является касательной к графику функции в точке (1; 2).

- Хорошо видно, что вблизи точки касания график функции практически сливается с касательной y=x+1.

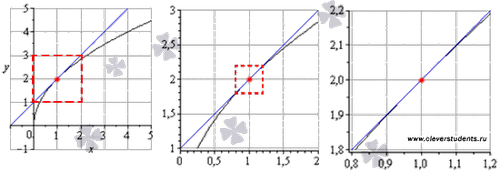
- На последнем рисунке кривая почти совпадает с прямой, то есть выглядит как отрезок прямой.

- С увеличением масштаба кривая приближается к прямой.

Учитель:

- Верно, с приближением к точке касания кривая спрямляется, почти сливаясь с касательной в точке касания. Это позволяет заменить график функции в окрестности практически любой его точки на график линейной функции. Именно на возможности такого упрощения и основан математический анализ.

Ситуация 5

Рассмотрите рисунок 25 в учебнике на стр.35 (см приложение №1) и опишите его.

( Ученики рассматривают рисунки и делают выводы).

На рисунке 25(а) точка M₀ взята в прямоугольник. Этот прямоугольник вместе с тем, что оказалось внутри него увеличен на рисунке 25(б). Следующее увеличение приводит к рисунку 25(в).

Учитель:

- Эти рисунки позволяют дать определение касательной, которое подойдёт и к окружности, и к другим кривым. Попробуйте его сформулировать самостоятельно, а затем свериться с тем, что написано в учебнике.

- Прочитайте определение касательной в учебнике.

Ситуация 6

Рассмотрите рисунки 27 и 28 учебника на стр.35 (см приложение №1).

Учитель:

- Всегда ли существует касательная к графику функции?

Сформулируйте две основные ситуации отсутствия касательной.

7. Применение новых знаний на практике.

Устно № 53(приложение 2).

Письменно № 54 (1, 2) (приложение 2).

(К доске вызываются последовательно два ученика и на крыльях выполняют эти задания, а затем они проверяются с применением карточек обратной связи.)

Примечание (для учителей)

Желательно, чтобы дети, как можно раньше (может быть, на этом этапе) поняли, есть ли различие слов «построить» и «провести», «нарисовать», «изобразить», и могли раскрыть, в чем оно заключается. Обратите на это внимание, поговорив с детьми на эту тему. Ведь нам не всегда нужны графики, часто достаточно эскиза, схематического изображения. Полезно спрашивать всякий раз ребят с аргументацией: а на рисунке схема или график.

9. Домашнее задание (по выбору).

1. Подготовить сообщение на тему: «И. Ньютон и Г.В.Лейбниц - открытие метода исчисления бесконечно малых промежутков».

2. Нарисовать график произвольной функции, выбрать 4 точки, провести касательные к этим точкам.

3. Выполнить письменно №51.

10. Подведение итогов урока. Рефлексия.

10.1. Достижение личностных результатов.

- Ребята, в начале урока Вы поставили личную цель. Достигли её Вы или нет? Кто хочет, поделитесь своими выводами вслух?

Демонстрируется слайд с личностными целями.

10.2. Достижение предметных и метапредметных результатов:

Вопросы к учащимся:

1. Что нового Вы узнали сегодня на уроке?

2. Чему Вы научились?

В помощь детям учитель открывает слайды (содержание слайдов ниже) с планируемыми результатами. Опираясь на них, дети отвечают на вопросы.

Содержание слайдов

Результаты:

Предметные:

- понимание смысла понятия «касательная к графику функции»;

- умение осознанно употреблять новое понятие в устной и письменной речи;

- овладение опытом построения касательной к графику функции;

- осознанное употребление нового математического понятия в устной и письменной речи;

- овладение опытом построения касательной к графику функции в простых случаях, опираясь на использование уже имеющихся знаний;

- приобретение способности «открывать» новое математическое знание;

-понимание сути и осознанное использование математических средства наглядности (рисунки и чертежи) для иллюстрации и аргументации собственных рассуждений и действий;

- умение формулировать учебную тему и учебные задачи, используя математическую терминологию.

Познавательные:

- сравнение, сопоставление, классификация, ранжирование объектов по одному или нескольким признакам;

- комбинирование известных алгоритмов деятельности в ситуациях, не предполагающих стандартного применения одного из них;

- исследование несложных практических ситуаций, выдвижение предположений, понимание необходимости их проверки на практике;

- умение мотивированно отказаться от образца, искать оригинальное решение;

- умение разделять процессы на этапы и звенья;

- использование различных методов (опыт, наблюдение).

Информационно - коммуникативные:

- умение вступать в речевое общение, участвовать в диалоге;

- отражение в устной и письменной форме результатов своей деятельности;

- умение перефразировать мысль, анализировать, аргументировать сделанный вывод;

- проведение информационно - смыслового анализа задания;

- приведение примеров, подбор аргументов, формулирование выводов.

Рефлексивные:

- поиск и устранение причин возникших трудностей;

- оценивание своих учебных достижений;

- умение работать в парах и индивидуально;

- умение ставить личностные цели и оценивать степень их достижения.

Вопросы к учащимся (продолжение):

3. Что вызвало затруднение и почему?

4.Что Вам понравилось на уроке?

5. Подсчитайте количество баллов и оцените свою работу.

Система оценивания:

«7 баллов и более» - 5;

«4-6 баллов» - 4;

«1 -3 балла» -3;

«0 баллов» - 2.

Ребята, сегодня первый урок изучения новой темы, поэтому главное, что вы поняли смысл нового понятия и участвовали в «открытии» нового знания. Поэтому в журнал я выставлю только отличные и хорошие отметки.

На следующем уроке мы продолжим работу, познакомимся с другими новыми понятиями.

Р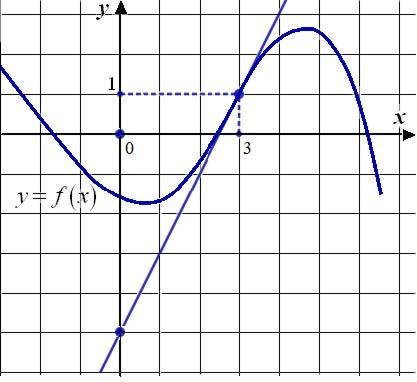ебята, вы все хорошо поработали, спасибо за урок!