Урок по математике в 7 классе «Квадрат суммы и разности двух выражений»

Урок по математике в 7 классе «Квадрат суммы и разности двух выражений»

учитель математики

МБОУ «Первомайская СОШ»

Нагуманова Светлана Петровна

Проект урока (в рамках ФГОС)

Класс:7

Предмет: математика

Тема урока: Квадрат суммы и разности двух выражений

Тип урока: урок открытия нового знания

Цели и задачи урока:

вывод формул квадрата суммы и квадрата разности двух

выражений; отработка навыка применения данных формул

развитие логического мышления и мировоззрения учащихся

воспитание у школьников устойчивого интереса к математике

Учебник для 7 класса общ. Учр.: Макарычев Ю.Н. Миндюк Н.Г и др под редакцией Теляковского С.А.

М.,Просвещение, 2009 г.

Этап урока

Содержание

Деятельность учителя

Деятельность учащихся

ПР: личностные, предметные, метапредметные

Мотивирование к учебной деятельности

Формирование групп для самостоятельной работы

Организует мотивацию, создает условия для возникновения внутренней потребности включения в учебную деятельность (сегодня вы выступите в роли исследователей)

Распределяют позиций в группе

ориентация учащихся в социальных ролях и межличностных отношениях, процесс адекватного самоопределения планирование учебного сотрудничества с учителем и сверстниками;

Актуализация знаний и фиксирование затруднения в пробном учебном действии. Выявление причины затруднения

Устный счет

Дает задания на повторение и закрепление темы предыдущих уроков. Задает вопрос: В чём возникло затруднение?- Прочитайте выражения. Знаем ли мы эти формулы? А хотим узнать?

- Так какие же формулы мы сегодня должны «открыть»?

- Итак, сформулируйте тему нашего сегодняшнего урока.

Цели нашего урока?

Повторяют изученные сведения.

Формулируют тему урока и цели урока.

Вступают в беседу, отвечают на вопросы, фиксируют операцию, где возникло затруднение

Демонстрируют вычислительные навыки и навыки работы с многочленами

умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами

-коррекция - внесение необходимых дополнений ;
-оценка - выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.

Открытие нового знания

1.Построение проекта выхода из затруднения

2.Реализация построенного проекта

Заполнение таблицы

Руководит процессом с помощью подводящего и побуждающего диалогов

Обдумывают проект будущих учебных действий:

Ставят цель, выбирают способ, строят план достижения цели и определяют алгоритмы .

Осмысленно читают, извлекая нужную информацию., обсуждают различные варианты, выбирают оптимальный.

Самостоятельно работают с заданием упражнения.

Фиксируют преодоление ранее возникшего затруднения

Осуществляют самоконтроль с использованием элементов самооценки.

- целеполагание как постановка учебной задачи ;
-планирование - определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий;
прогнозирование - предвосхищение результата и уровня усвоения.

Умение анализировать , доказывать и аргументировать ход и способ действий, умение делать выводы

- управление поведением партнера - контроль, оценка действий партнера;

умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации

Первичное закрепление

Предлагает вернуться к возникшей проблеме устном задании и сравнить выражения

Сравнивают выражения

проговаривание во внешней речи

построение логической цепи рассуждений.

выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;

Самостоятельная работа с самопроверкой

Решение задач из учебника

Предлагает решить задания из учебника несколькими способами

2 человека решают у доски на «скрытых» досках

Остальные учащиеся решают самостоятельно

Сравнивают полученные результаты

Решение типовых заданий на новый алгоритм

Проговаривание алгоритма вслух

Рефлексия учебной деятельности

Подведение итогов урока

Задает вопросы:-Итак, какую тему мы сегодня изучали?- Что удалось ?-Что вызвало трудности? И т. Д. Предлагает оценить свою

работу на уроке + или _

Благодарит за проделанную работу.

Рекомендует выполнить дома: два номера для всех и 1 для желающих (с опережением)

Анализируют и оценивают свою учебную деятельность на уроке

соотносят цели и результаты

Осуществляют пошаговый контроль по результату, намечают дальнейшие действия

рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности;
-оценка - выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.

умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации;

- владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка.

Приложение: устный счет: (на слайдах)

1) Прочитайте выражения:

а) х²-(5у)²; б) (2х73у)²; в) х² + (4у)²; г) (а - 3в)²; д) 2(m∙3n); е)(с-7d)(c+7d).

2) Возведите в квадрат: а) 5у б) 0,4х²у³

в) 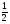х³у

- Найдите произведение 2х и 0,8х³у² ; найдите удвоенное произведение этих выражений.

3) Решите уравнение: а) х² - 81 = 0; б) х² + 81 = 0

4) Вычислите: а) (50 - 3)(50 + 3) в) 108 ∙ 192

б) 248² - 247²

5) Сравните: а) 123185 ∙ 123187 и 123186²;

б) 89² + 95² и (89 + 95)²;

в) 60² + 49² и (60 -49)².

- В чём возникло затруднение?

- Прочитайте выражения. Знаем ли мы эти

формулы? А хотим узнать?

- Так какие же формулы мы сегодня должны «открыть»?

- Итак, сформулируйте тему нашего сегодняшнего урока. Цели нашего урока?

Приложение: «Открытие » нового знания

1,3 группы

Умножение многочлена на многочлен

Раскрытие скобок

Приведение подобных слагаемых

Результат

(х+6)(х+6)

(8+у)(8+у)

(2х+5)(2х+5)

И т.д.

Обратите внимание на задания и ответьте на вопросы:

- Что общего в задании?

- Как произведение одинаковых множителей записать в виде степени?

- Что общего в полученных ответах?

- Запишите соответствующую формулу?

- Сформулируйте полученное правило возведения суммы двух выражений в квадрат.

2,4 группы: (квадрат разности двух выражений)

- В чём различия результатов, если возводим в квадрат не сумму, а разность двух

выражений?

- Запишите соответствующую формулу.

Сформулируйте полученное правило возведения разности двух выражений в квадрат.