- Учителю
- Пакет контрольно-измерительных материалов по алгебре для 9 класса
Пакет контрольно-измерительных материалов по алгебре для 9 класса
|
|
| Пакет контрольно-измерительных материалов по алгебре |
| IX класс |
|
|
| Подготовил: Даудов С.Ш. |
|
|
Астрахань 2013 год
Алгебра 9 класс.
Зачетный раздел №1
Пояснительная записка
Цель: Выработать умение строить графики квадратичной функции и применять графические представления для решения неравенств второй степени с одной переменной.
Тематическое планирование
Тема №1 Квадратичная функция.
Форма проведения по билетам с элементами выполнения практических заданий.
Литература: Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра. Учебник для учащихся 9 класса общеобразовательных учреждений М. «Просвещение» - 2001.
Требования к учащимся на зачете.
В результате изучения зачетного раздела на базовом уровне ученик должен:
-
Понимать, что функция - это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами, что конкретные типы функций (квадратичная функция) описывают большое разнообразие реальных зависимостей.
-
Находить значение функций, заданных формулой, таблицей, графиком; решать обратную задачу.
-
Находить по графику функций промежутки возрастания и убывания функций, промежутки знакопостоянства, наибольшее и наименьшее значения.
-
Строить график квадратичной функции.
-
Интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы.
Вопросы и задания
§ 1 п. 1,2
-
Дайте определение функции. Что называется областью определения и областью значений функции?
-
Что называется графиком функции?
-
Дайте определение функции, возрастающей в промежутке; убывающей в промежутке.
§ 2 п. 3,4
-
Дайте определение квадратного трехчлена. Сколько корней может иметь квадратный трехчлен?
-
Сформулируйте и докажите теорему о разложении на множители квадратного трехчлена, имеющего корни.
§ 3 п. 6,7
-
Сформулируйте определение квадратичной функции.
-
Сформулируйте свойства квадратичной функции y=ax2: а) при a>0; б) при a<0.
-
Как из графика функции y=ax2 можно получить график функции y=ax2+n; график функции y=a(x-m)2?
-
Как из графика функции y=ax2 можно получить график функции y=a(x-m)2+n?
-
Что представляет собой график функции y=ax2+bx+c?
Практические задания.
-
Используя рисунок, поясните, как с помощью графика функции найти нули функции и промежутки, в которых функция сохраняет знак (принимает положительные значения, отрицательные значения).
y
0 x
-
Назовите промежутки возрастания и убывания функции, график которой изображен на рисунке.
-
Покажите на примере выражения 3x2+12x+32, как можно выделить квадрат двучлена из квадратного трехчлена.
-
На примере функции y = 2x2-12x+16 покажите, как строят график квадратичной функции.
-
На примере неравенств 3x2+5x-2<0 и x2+2x+6>0 расскажите, как можно решить неравенство второй степени, используя свойства квадратичной функции.
-
На примере неравенства (x-5)(x+7)(x+9)<0 расскажите как неравенства методом интервалов.
Зачетный раздел №2
Пояснительная записка
Цель: Выработать умение решать простейшие системы, содержащие уравнения второй степени с двумя переменными и решать тестовые задачи с помощью составления таких систем.
Тематическое планирование
Тема №2 Уравнения и системы уравнений.
Форма проведения по билетам с элементами выполнения практических заданий.
Литература: Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра. Учебник для учащихся 9 класса общеобразовательных учреждений М. «Просвещение» - 2001.
Требования к учащимся на зачете.
В результате изучения зачетного раздела на базовом уровне ученик должен:
-
Понимать, что уравнения - это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики.
-
Правильно употреблять термины: «уравнение», «неравенство», «система», «корень уравнения», «решение системы». Понимать их в тексте, в речи учителя, понимать их в тексте, в речи учителя, понимать формулировку задачи «решить уравнение, неравенство, систему».
-
Решать линейные, квадратные уравнения и простейшие рациональные уравнения, сводящиеся к ним, системы уравнений с двумя переменными (линейные системы, в которых одно уравнение второй степени).
-
Решать линейные неравенства с одной переменной и их системы, неравенства второй степени.
-
Решать текстовые задачи с помощью составления уравнений.
Вопросы и задания
§ 5 п. 10,11
-
Какое уравнение с одной переменной называется целым. Приведите пример.
-
Как найти степень целого уравнения? Сколько корней может иметь уравнения с одной переменной первой степени; второй степени?
-
Дайте определение биквадратного уравнения. Объясните, как решают биквадратные уравнения?
§ 6 п. 12,14
-
Объясните, в чем состоит графический способ решения системы уравнений с двумя переменными.
-
Покажите на примере, как используя способ подстановки, можно решить систему уравнений с двумя переменными, одно из которых первой степени, а другое второй.
Практические задания.
-
Решите уравнение графически.
x3+x-4=0.
-
При каких значениях p уравнение 3x2 + 2px + 5 = 0 имеет два корня?
-
Решите биквадратное уравнение 9x4 - 10x2 + 1 = 0.
-
Решите систему уравнений
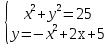
-
Решите систему уравнений
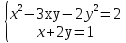
Зачетный раздел №3
Пояснительная записка
Цель: а) Дать понятие об арифметической и геометрической прогрессиях как числовых последовательностях особого вида;
б) Ввести понятие корня n-й степени;
в) Ввести понятия синуса, косинуса, тангенса и котангенса произвольного угла; сформировать умения вычислять значения тригонометрических функций по известному значению одной из них; выполнять несложные преобразования тригонометрических выражений.
Тематическое планирование
Тема №3,4,5 Степенная функция. Корень n-й степени. Тригонометрические выражения. Прогрессии.
Форма проведения по билетам с элементами выполнения практических заданий.
Литература: Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра. Учебник для учащихся 9 класса общеобразовательных учреждений М. «Просвещение» - 2001.
Требования к учащимся на зачете.
В результате изучения зачетного раздела на базовом уровне ученик должен:
-
Понимать, что прогрессии - это числовые последовательности особого вида.
-
Правильно употреблять термины «рекуррентный», «разность прогрессии», «знаменатель прогрессии».
-
Находить по формулам любой член прогрессии, сумму членов прогрессии.
-
Находить по графику функции промежутки возрастания и убывания функции.
-
Строить график степенной функции.
-
Знать определение четной и нечетной функции.
-
Знать свойства степенной функции и особенности ее графика при любом натуральном n.
-
Правильно употреблять термины «показатель корня», «подкоренное выражение».
-
Знать и уметь применять свойства арифметического корня n-й степени.
-
Знать и уметь применять свойства степени с рациональным показателем.
-
Выполнять действия со степенями натуральным, целым и дробным показателями.
-
Знать определение синуса, косинуса, тангенса и котангенса угла и их свойства.
-
Знать и уметь применять основные тригонометрические формулы к преобразованию выражений.
Вопросы и задания
§ 7 п. 15,17
-
Приведите пример последовательности, заданной
а) формулой n-го члена; б) рекуррентной формулой. Найдите пять первых членной последовательности.
-
Сформулируйте определение арифметической прогрессии. Какое число называют разностью арифметической прогрессии?
-
Запишите формулы n-го члена и суммы n первых членов арифметической прогрессии.
§ 8 п. 18,20
-
Сформулируйте определение геометрической прогрессии. Что называют знаменателем геометрической прогрессии?
-
Запишите формулы n-го члена и суммы n-первых членов геометрической прогрессии.
-
Чему равна сумма бесконечной геометрической прогрессии, у которой
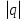 < 1?
< 1?
§ 9 п. 21,22
-
Дайте определение четной функции. Сформулируйте свойства графика четной и нечетной функции.
-
Какую функцию называют степенной функцией с натуральным показателем?
-
Сформулируйте свойство степенной функции с четным показателем. Покажите схематически, как выглядит график этой функции.
-
Сформулируйте свойства степенной функции с нечетным показателем n и докажите их. Покажите схематически, как выглядит график этой функции при n > 1.
§ 10-11 п. 23-27
-
Дайте определение корня n-й степени и арифметического корня n-й степени.
-
Сформулируйте свойства арифметического корня n-й степени докажите одно из них.
-
Дайте определение степени с дробным показателем.
-
Сформулируйте свойства степени с рациональным показателем. Докажите, что если a > 0, p и q -любые рациональные числа,
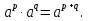
§ 12-14 п. 28-36
-
Дайте определение синуса, косинуса, тангенса и котангенса угла
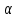 .
. -
Какие знаки имеют синус, косинус, тангенс и котангенс в каждой из координатных четвертей?
-
Какие из тригонометрических функций являются четными, какие - нечетными? Выразите в радианах углы, равные 30°, 45°, 60°, 90°, 180°, 270°, 360°.
-
Запишите формулу, выражающую связь между синусом и косинусом одного и того же угла.
-
Запишите формулы, выражающие тангенс и котангенс через синус и косинус. Приведите доказательство.
-
Выведите формулы:
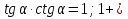
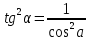 ; 1 + ctg2α =
; 1 + ctg2α = 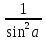
-
Запишите формулы приведения для углов
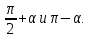
-
Запишите формулу косинуса разности двух углов. Выведите из нее формулы косинуса суммы, синуса суммы и синуса разности.
-
Напишите формулы синуса и косинуса двоичного угла. Приведите доказательство.
-
Напишите формулу преобразования в произведение суммы и разности синусов, суммы и разности косинусов. Приведите доказательство одной из этих формул.
Зачётный раздел № 4
Пояснительная записка
ЦЕЛЬ: Ознакомить учащихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчёта их числа; ввести понятия относительной частоты и вероятности случайного события.
Тематическое планирование
Тема №5. «Элементы комбинаторики и теории вероятностей»
Тема №6. «Повторение. Решение задач по курсу алгебры 7 - 9 классов»
Форма проведения по билетам с элементами практических заданий.
ЛИТЕРАТУРА: С.А. Теляковский, Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков,
С.Б. Суворова. Алгебра. 9 класс: учебник для общеобразовательных учреждений. М. Просвещение. 2010 г.
Требования к учащимся на зачёте:
1. Применять комбинаторное правило умножения.
2. Применять формулы для подсчёта числа перестановок, размещений и сочетаний.
3. Различать понятия «размещение» и «сочетание».
4. Владеть понятиями «случайное событие», «относительная частота», «вероятность случайного события».
5. Различать статистический и классический подходы к определению вероятности случайного события.
6. Владеть понятием « равновозможное событие».
7. Владеть понятиями «несовместимые события» и « независимые события».
Раздел
учебника
Единица
усвоения
Вопросы и задания
Глава 5
§11 п30
1,2
Уметь составлять комбинации элементов и подсчитать их число.
§11 п30
1
Дать определение - комбинаторное правило умножения.
§11 п 31
2,3
Дать определение перестановки из трёх элементов.
§11 п 32
2,3
Дать определение размещения из четырёх элементов по три.
§11 п 33
2,3
Дать определение сочетания из n элементов по k.
§12 п 34
1,2,3
Определить о каком виде комбинаций идёт речь в задаче.
§12 п 34
4
Раскрыть сущность понятия «случайное событие».
§12 п 34
4
Раскрыть сущность понятия « относительная частота»
§12 п 34
4,5
Раскрыть сущность понятия «вероятность случайного события»
§12 п 35
6
Дать определение вероятности равновозможных событий.
§12 п 36
7
Дать определение несовместимых событий.
§12 п 36
7
Дать определение независимых событий.
§12 п 36
7
Произвести сложение вероятностей.
§12 п 36
7
Произвести умножение вероятностей.
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
1. Сложить дроби 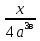 и
и 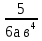
2. Преобразовать (3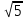 - 6
- 6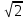 )(
)(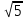 + 2
+ 2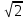 )
)
произведение
3.Решить уравнение 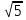 +
+ 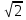 =
= 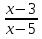
4.Решить систему неравенств 3х - 2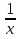 25
25
1 - х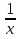 0
0
5.Упростить выражение 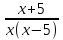
6.Упростить выражение
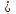
7.Найдите сумму первых пяти членов геометрической прогрессии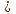 ), если
), если
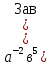 =121,5
=121,5

 Вечерняя (сменная) общеобразовательная школа №10
Вечерняя (сменная) общеобразовательная школа №10