- Учителю
- Разноуровневый урок алгебры в 9 классе «Обобщающее повторение формул сокращённого умножения»
Разноуровневый урок алгебры в 9 классе «Обобщающее повторение формул сокращённого умножения»
Разноуровневый урок алгебры в 9 классе:
«Обобщающее повторение формул сокращённого умножения»
Класс разделён на три группы в соответствии с уровнем усвоения материала по данной теме.
1группа - учащиеся, которые справляются с заданиями по данной теме на 80-100%.
2 группа- учащиеся, которые справляются с заданиями по данной теме на 60-80%.
3 группа- учащиеся, которые справляются с заданиями по данной теме ниже 60%.
Цель урока: обобщить теоретические знания по теме «Формулы сокращённого умножения», рассмотреть решение задач, связанных с этой темой базового и повышенного уровней сложности, показать учащимся широкий спектр применения формул.
Организовать работу учащихся по указанным темам на уровне, соответствующем уровню уже сформированных знаний.
І этап урока - организационный (1 мин).
Слайд1. Учитель сообщает учащимся тему урока, цель. Поясняет, что во время урока постепенно будет использоваться раздаточный материал.
ІІ этап урока (7 мин).
Повторение теоретического материала по теме: «Формулы сокращённого умножения».
Учитель: «Назовите формулы сокращённого умножения, которые вы знаете».
Ответ: квадрат суммы и разности, разность квадратов, сумма и разность кубов.
Для повторения формул используется мультимедийная презентация. На экране последовательно появляются левые части формул и после ответа к ним присоединяются правые части.
Слайд2: 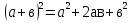
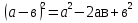
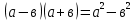
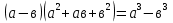
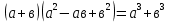
Учитель: устно выполните следующие тестовые задания (учащиеся отвечают с помощью сигнальных карточек 1,2,3,4).
Для учащихся допустивших ошибку задание комментируется одним из учащихся.
Слайд 3: 1.Преобразуйте выражения:
а) (х+2)² б) (2а-3)² в) (3а+в)²
1. х²+2х+4 1. 4а²-6а+9 1. 9а²+в²
2. х²+4х+4 2. 2а²-12а+9 2. 3а²+6ав+в²
3. х+4+4х 3. 4а²-12а+9 3. 9а²+3ав+в²
4. х²+4 4. 4а²-9 4. 9а²+6ав+в²
г) (2х-3у)(2х+3у) д) (х-1)(х²+х+1)
1. 2х²-3у² 1. х²-1
2. 4х²-6у² 2. х²-2х+1
3. 4х²-9у² 3. х³-1
4. 4х²+9у² 4. х-1
Слайд 4: 2. Сократите дробь:
а) в²-4а² б) 2х-у . у³
2а-в 0,3у у²-4х²
1. в+2а 1. ____у_____
2. 2а-в -0,3(2х+у)
3. в-2а 2. _ ____у²_____
4. -в-2а 0,3(у+2х)
3. _у²__
у+2х
4. ____у____
0,3(у-2х)
Слайд 5: 3. Решить уравнение:
а) х²-9=0 б) х²-10х+25=0
1. + 3 1. 0 ; 5
2. 3 2. -5
3. корней нет 3. +5
4. -3 4. 5
ІІІ этап (25 мин). Работа в разноуровневых группах.
Со всеми учащимися класса рассматриваются задания на преобразование алгебраических выражений.
№1. Упростить выражение:
а) 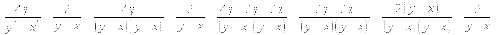
б) 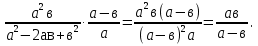
№2. Учитель предлагает учащимся ответить на вопрос: «График какой функции изображен на рисунке?»
Слайд 6.
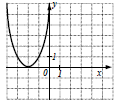
1) у = х²+4; 2) у = -х²+4; 3) у = -(х+2)(х+2); 4) у = х²+4х+4.
При ответе на вопрос учитель просит учащихся комментировать свои ответы или (если ученик затрудняется) комментирует сам.
Учитель говорит , что далее он продолжит коллективную работу с учащимися 1 группы, а учащиеся 2-й и 3-й группы приступают к выполнению заданий по карточкам (синяя и зелёная карточки с №1)
Карточка №1 (синяя -3 группа).
1. Преобразуйте выражение:
а) 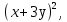 б)
б) 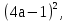 в)
в) 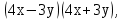
1.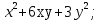 1.
1. 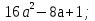 1.
1. 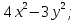
2. 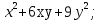 2.
2.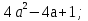 2.
2.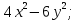
3. 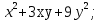 3.
3.  3.
3. 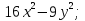
4. 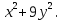 4.
4. 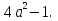 4.
4. 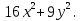
2. Решите уравнение:
а) 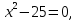 б)
б) 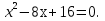
3. Сократите дробь: 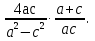
Карточка №1 (зелёная -2 группа)
1. Преобразуйте выражение:
а) 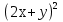 б)
б) 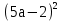 в)
в) 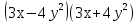
1.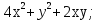 1.
1. 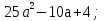 1.
1. 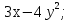
2. 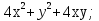 2.
2.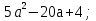 2.
2.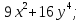
3. 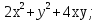 3.
3. 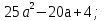 3.
3. 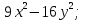
4. 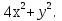 4.
4. 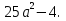 4.
4. 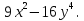
2. Решите уравнение:
а) 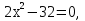 б)
б) 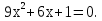
3. Сократите дробь: 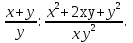
4. Построить график функции: 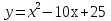 .
.
Работа с 1 группой:
Учитель предлагает учащимся 1-й группы построить график функции, преобразовав выражение с помощью формул.
1. Построить график функции: 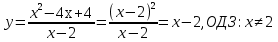
Учащиеся выполняют построение, комментируя все шаги решения.
2.Учитель предлагает решить уравнение и указать его наибольший корень. Ученик решает на доске, обсуждая все шаги решения.
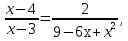
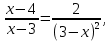
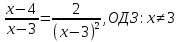
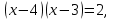
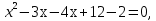
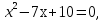
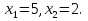
5-наибольший корень.
Ответ: 5.
После обсуждения и решения этих задач учащиеся 1 группы приступают к выполнению самостоятельной работы (красная карточка)
Красная карточка.
1. Найдите значение выражения:
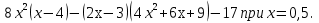
2. Выполните действия:
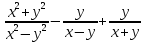
3. Решите уравнение и вычислите произведение корней:
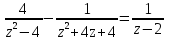
4. Постройте график функции: 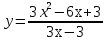
В это время для учащиеся 2-й и 3-й групп на экране высвечиваются справильные ответы на задания карточек №1 (синей и зелёной). Учащиеся сверяют свои ответы (слайд 7) и при необходимости обращаются к учителю за пояснением.
ІV этап (10 мин).
С учащимися 2-й и 3-й групп разбираются две задачи:
№1. Упростить выражение:
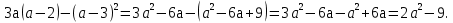
№2. Решить уравнение:
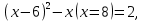
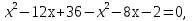
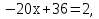
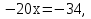
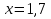
Ответ: 1,7.
Далее учащиеся 2-й и 3-й групп приступают к самостоятельной работе:
Карточка №2 (синяя).
1. Сократите дробь: 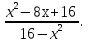
2. Упростить: 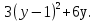
3. Решите уравнение: 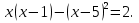
Карточка №2 (зелёная).
1. Выполнить действия: 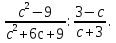
2. Упростить: 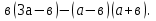
3. Решить уравнение: 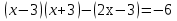
По истечении времени учащиеся всех групп сдают работы.
V этап. (2 мин).
Подведение итогов урока, комментарии по домашнему заданию.
Учитель ещё раз обращает внимание на те теоретические факты, которые вспоминали на уроке, говорит о необходимости выучить их. Отмечает наиболее успешную работу на уроке отдельных учащихся при необходимости выставляет оценки.
В качестве домашнего задания выдаются варианты краевых контрольных работ, учащимся 2-й группы предлагаются по желанию красные карточки, а учащимся 3-й карточки зелёные.