Производная в материалах ЕГЭ

Урок : «Алгебра и начала анализа», 11 класс

Тема: «Производная в материалах ЕГЭ"

Эпиграф: «Величие человека - в его способности мыслить»

(Б. Паскаль)

Цели урока:

Дидактическая:

• повторение сформированных умений и навыков, являющихся банком знаний;

• закрепление и систематизирование знаний учащихся по исследованию функций с помощью производной;

• содействовать усвоению учащимися применения производной в практических заданиях

Развивающая:

• продолжить развитие алгоритмического мышления, памяти и мировоззрения учащихся, умения делать выводы и обобщать;

• развитие устной и письменной речи;

• становление и развитие личностных характеристик

Воспитательная:

• воспитание нравственности и самостоятельности;

• воспитание на уроке воли и упорства для достижения конечных результатов, уважительного отношения друг к другу.

Тип урока: применение знаний, умений, навыков

Вид урока: математический турнир

Методы проведения урока: словесный, наглядный, практический

Оборудование: тетради, опорные конспекты, ручки, раздаточный материал, мел, доска, чертежные инструменты, таблица производных-плакат

ХОД УРОКА

1. Организационный момент

Класс делится на две команды заранее, выбирают капитанов, придумывают название

2. Сообщение темы урока, постановка целей

Согласно ФГОС среднего (полного) общего образования, цель образования - не только сумма знаний и компетенций, но и, в числе прочих, - становление и развитие таких личностных характеристик выпускника, как уважение мнения других людей, умение вести конструктивный диалог, достигать взаимопонимания и успешно взаимодействовать. Все это поможет выпускнику в дальнейшем стать действительно успешной и гармоничной личностью, сочетающей в себе образованность и внутреннюю культуру.

Поэтому, сегодня мы проведем математический турнир, т.е. соревнование двух команд в решении математических задач, в ходе которого вы будете учиться совместно решать поставленные задачи и вести конструктивную полемику по предложенной проблеме, тем самым будете развивать свои мыслительные способности, настойчивость в выполнении заданий и применять творческий подход к решению задач.

I ТУР - РАЗМИНКА

В течение 3 минут вспомнить как можно больше терминов математики на букву П. За каждый термин - 1 балл

II ТУР - АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ

Проверка теоретических знаний: по очереди от каждой команды выходят по одному участнику. Снимают с доски по одному листочку и отвечают на вопрос на обороте. Если участник не отвечает на вопрос ( - 1 балл) и у другой команды есть возможность ответить.

Вопросы:

1. Чему равна производная константы с? с^=0

2. Чему равна производная kx? (kx)^=k

3. Чему равна производная х^p? (x^p)=px^p-1

4. Чему равна производная sinх? (sinx)^=cosx

5. Чему равна производная cosх? (cosx)^=-sinx

6. Чему равна производная e^x? (e^x)^=e^x

7. Чему равна производная lnх? (lnx)^=1/x

8. Чему равна производная произведения uv? (uv)^=u^v+uv^

9. Чему равна производная частного u/v? (u/v)^= (u^v-uv^)/v²

10. Геометрический смысл производной?

Геометрический смысл производной состоит в том, что значение производной в точке равно угловому коэффициенту касательной к графику функции в этой точке-f(x₀)=k=tgα

11. Механический смысл производной?

Механический смысл производной состоит в том, что скорость движения тела в момент времени есть производная пройденного пути, а ускорение движущегося тела есть вторая производная пути, т.е. v(t)=S^(t); a(t)=S^(t);

12. Какая стационарная точка является точкой максимума?

Если при переходе через стационарную точку производная меняет знак с «+» на «-», то эта точка является точкой максимума.

13. Какая стационарная точка является точкой минимума?

Если при переходе через стационарную точку производная меняет знак с «-»на, «+» то эта точка является точкой минимума.

14. Как определить промежутки возрастания и убывания функции?

Если производная положительна на промежутке, то функция возрастает на этом промежутке; если отрицательна, то убывает.

III ТУР - УСТНАЯ РАБОТА С КОМАНДАМИ

Отвечают по очереди из каждой команды

Вычислить производную:

1. у = - 3 (0)

2. у = 2х - 3 (2)

3. у = х² - 3х + 4 (2х-3)

4. у = 1/5х⁵ - 7х + 4 (х⁴-7)

5. у = sin(9x+1) (9cos(9x+1))

6. у = 11cosx (-11sinх)

7. у = 1/3 sin3x (cos3x)

8. у = cos4x - 6 (-4 sin4x)

9. у = е^7х (7е^7х)

10. у =1/4 е^4х-5 (е^4х-5)

11. у = (х - 3)² (2(х-3))

12. у = (3 - 4х)² (-8(3-4х))

13. у = ln(х-5) (1/(х-5))

14. у = 1/2 ln(1+2х) (1/(1+2х))

IV ТУР  МАТЕМАТИЧЕСКОЕ ЛОТО

Задача, конечно, не слишком простая:
Играя учить и учиться играя.
Но если с учебой сложить развлеченье,
То праздником станет любое ученье!

Каждой команде выдается групповое задание: на листе - 6 заданий подобных заданию 8 из демонстрационной версии профильного уровня 2015. К этому заданию прилагаются карточки с ответами. Необходимо, решив задание, выбрать подходящую карточку и накрыть ею задание. В результате должно получиться изображение (Приложение 1).

V ТУР  КОНКУРС КАПИТАНОВ И РАЗГАДАЙ СЛОВО

Капитанам команд выдаётся задание, которое они решают независимо от команды (задание 14, профильный уровень ЕГЭ). В это время все члены команды также получают индивидуальное задание с выбором ответа. Если задание решено верно, то в итоге получается слово. Если буква не вписывается в слово, значит, пример решен не верно.

Задание для капитанов: (Приложение 2).

Капитан 1 команды

Найдите наибольшее значение функции на отрезке -3;5

Ответ: 11

Капитан 2 команды

Найдите наименьшее значение функции на отрезке -5;0

Ответ: -51

Задание для 1 команды:

1

Найти производную

f(х) = х⁴+4х³-8х²-5

2

Найти производную

f(х) = х³-2х²-7х+1

3

Найти производную

f(х) = (х-2)²х³

4

Найти производную

f(х) = (х⁵+4х)(5-х²)

5

Найти производную

f(х) = (2х-1)/(7х+1)

6

Найти производную

f(х) = (5-4х)²/(х+1)

Ответы 1 команды (МОДУЛЬ)

Л

Д

Ь

9/(7х+1)²

5х⁴-16х³+12х²

(16х²+32х-65)/(х+1)²

О

М

У

3х²-4х-7

4х³+12х²-16х

-7х⁶+25х⁴-12х²+20

Задание для 2 команды:

1

Найти производную

f(х) = 2х⁵+4х²-7х-5

2

Найти производную

f(х) = х⁴-3х²+11х-1

3

Найти производную

f(х) = х (х-2)²

4

Найти производную

f(х) = (х⁷+4)(5-х)

5

Найти производную

f(х) = (3х-1)/(7+х²)

6

Найти производную

f(х) = (5-4х)/(7х³+1)

Ответы 2 команды (ГРАФИК)

К

Ф

Г

(56х³-105х²-4)/(7х³+1)²

-8х⁷+35х⁶-4

10х⁴+8х-7

А

Р

И

3х²-8х+4

4х³-6х+11

(-3х²+2х+21)/(7+х)²

Подведение итогов: по командам, личному первенству. Выставление оценок.

Домашнее задание: ЕГЭ 2015 (сайт Ларин А.А.) Вариант 105-107, задание 8, 14

ПРИЛОЖЕНИЕ 1

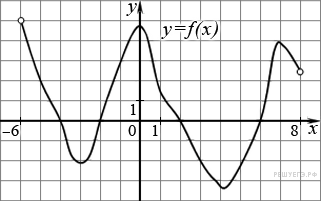
На рисунке изображен график функции , определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.

Прямая у=6х+11

параллельна касательной

к графику функции у=х²+7х-4.

Найдите абсциссу точки касания

На рисунке изображен график производной функции f(x), определенной на интервале (−11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

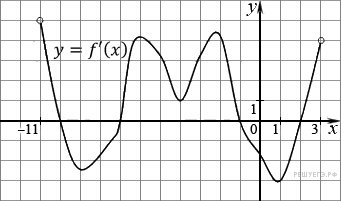
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].

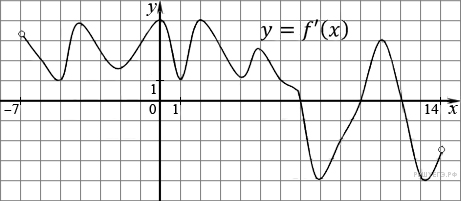
На рисунке изображён график производной функции и восемь точек на оси абсцисс: , . В скольких из этих точек функция возрастает?

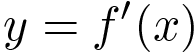
Тело движется по прямой так, что расстояние S ( в метрах) от него до данной точки этой прямой изменяется по закону S(t)=2t³-3t+4 (t-время движения в секундах). Найдите ускорение в момент времени t=2с.

4

-0,5

6

1

3

24

На рисунке изображен график функции , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции отрицательна

Прямая у=5-3х

параллельна касательной

к графику функции у=х²+6х+5.

Найдите абсциссу точки касания

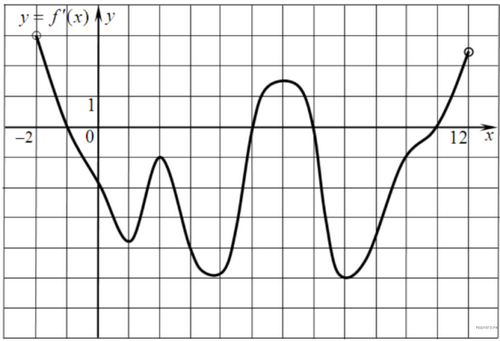
На рисунке изображен график производной функции f(x), определенной на интервале (−2; 12). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

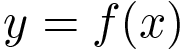
На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек минимума функции на отрезке .

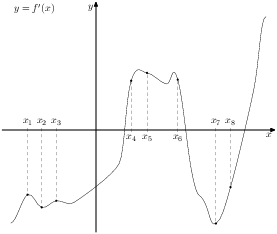
На рисунке изображён график производной функции и восемь точек на оси абсцисс: ,. В скольких из этих точек функция убывает?

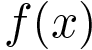
Тело движется по прямой так, что расстояние S ( в метрах) от него до данной точки этой прямой изменяется по закону S(t)=2t³-3t+4 (t-время движения в секундах). Найдите скорость в момент времени t=2с.

7

-4,5

2

1

5

21

ПРИЛОЖЕНИЕ 2

Задание для капитанов:

Капитан 1 команды

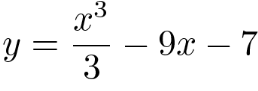
Найдите наибольшее значение функции на отрезке -3;5

Капитан 2 команды

Найдите наименьшее значение функции на отрезке -5;0