Способы решения иррациональных уравнений в 11 классе

Методическая разработка.

«Методы решения иррациональных уравнений»

Алгебра и начала анализа 11 класс.

Работу выполнила

Баранцева Аполлинария

Васильевна учитель

математики МКОУ СОШ

с. Сорвижи Арбажского района

Кировской области

2015 год

Методы решения иррациональных уравнений

Алгебра и начала анализа 11 класс.

1. Определение. Иррациональным называют уравнение, содержащее переменную под знаком корня.

Следует помнить, что при решении иррациональных уравнений необходима проверка всех найденных корней путем их подстановки в исходное уравнение или нахождение ОДЗ и следующий анализ корней.

Методы решения иррациональных уравнений.

1. Метод возведения обеих частей уравнений в одну и ту же степень, n- чётное число.

Часто применяется теорема: при натуральном n = равносильно системе f(x) = (²ⁿ,

0

Пример:

1. = 2 ОДЗ: х² - 5 0
   
   х²- 5 = 4
   
   х²= 9
   
   х = 3 х = -3 ОДЗ
   
   Ответ 3 ; -3

2. = х - 2 ОДЗ: х0
   
   х - 2
   
   х = (х -2)²
   
   х = х²- 4х + 4х
   
   х² -5х + 4 = 0
   
   х =1 х = 4 Проверка: 1-2 х = 1- посторонний корень
   
   = 4 - 2
   
   Ответ: 4

3. = ОДЗ: х - 6 0
   
   4- х 0
   
   х -6 = 4 - х
   
   2х = 10
   
   х = 5 Проверка: не существует, не существует.
   
   Ответ: нет корней.
   
   
   
   
   
   
   
   

4. = 3- х ОДЗ: 2х² - 12х + 17 0

3 - х 0

2х² - 12х + 17 = х² - 6х + 9

х² - 6х + 8 = 0

х₁ = 2 х₂ = 4 - посторонний корень, не принадлежит ОДЗ

Ответ: 2

Решить уравнения:

1. = 2х - 1

2. =

3. = - х- 1

4. Х² =

5. = 4

6. = 2

7. = 2

8. = 3

9. = 3

10. = х + 4

11. · = х + 3

12. · = х + 1

13. = х

14. х² = .

2. Метод «уединения» корня в одной из частей уравнения.

Пример1. - = 0 ОДЗ: 2х - 3 0

х + 2 0

= , возведём обе части уравнения в квадрат. Получим

2х - 3 = х+ 2

х = 5

Проверка: - = 0, то есть = 0. Так как получили верное числовое равенство, то х =5 - решение исходного уравнения.

Ответ: 5

2. + = 7 . «Уединим» в левой части и возведем полученное уравнение в квадрат:

= 7 -

х+4 = 49 - 14 · + 2х + 6. «Уединим» в левой части и полеченное уравнение вновь возведём в квадрат:

14 = х + 51

196(2х + 6) = х² + 102х + 2601

х²- 290х + 1425 = 0

х₁= 5 х₂= 285. Проверка показывает х= 285 - посторонний корень. Ответ: 5

Решить уравнения:

1. Х - = 5

2. - х = 3х - 4

3. - = 0

4. - х = 0

5. - 4 = х

6. - 2 = х

7. - х = - 3

8. - х - 2 = 0

9. -х+ 2 = 0

10. Х = 5 -

11. - 3 = х

Пример

2. = ОДЗ : х- 1 0

3х +1 0

х+ 3= ·

= х +3 ОДЗ: х+3 0

3х² - 2х - 1 = х² + 6х = 9

х²- 4х - 5 = 0

х₁= 5, х₂= - 1- не удовлетворяет ОДЗ

Ответ: 5

Решить уравнения:

1. =

2. =

3. =

4. =

5. =

6. =

7. + =

8. + =

Пример

3. - = 1 ОДЗ: 3х - 5

4 - х 0



= 1 + , возведём обе части данного уравнения в квадрат,

3х - 5 = 1 + 2 + 4 - х

2 = 3х + х - 5 -1 -4

2 = 4х - 10

= 2х - 5 ОДЗ: 2х - 5, возводим обе части последнего уравнения в квадрат

4 - х = (2х - 5)²

4 - х = 4х² -20 х + 25

4х²- 19 х + 21= 0

х₁ = 3 х₂ = 1, 75 - посторонний корень, т.к. х

Проверка:

= 1 +

2 = 1 + 1 - верно

Ответ: 3

Решить уравнения:

1. - = 1

2. + 2 = 5

3. - = 1

4. - 5 = 3 -

5. + = 7

6. = 2 +

7. + = 6

8. 2 = 15 -

3. Метод возведения обеих частей уравнений в одну и ту же степень, n- нечётное число.

Если уравнение имеет вид = g(x), то его можно решить, возведя обе части этого уравнения в степень n. Полученное уравнение f(x) = (g(x))ⁿ при нечётном n равносильно данному уравнению. При возведении в нечётную степень не происходит появления посторонних корней.

Пример

х =

х³ = х³ + х² - 6х + 8

Х² - 6х + 8 = 0

х= 4 х = 2

Ответ 2; 4

Решить уравнения

1. Х=

2. Х - 2

3. Х + 1 =

4. = 3

5. = 4

6. = 2

7. = -5

8. = 1 - ОДЗ: 1- х 0

Возведём обе части уравнения в куб:

2 - х = (1 - )³

2- х = 1-3 + 3( 1-х) - (1- х)·

1-3 + 3( 1-х) - (1- х)· - 2 +х = 0

-3 + 3( 1-х) - (1- х)· - (1-х) = 0

-3 +2( 1-х) - (1- х)· = 0

(-3 + 2 -1 + х) = 0

= 0 2 = 4- х ОДЗ: 4-х 0

1-х = 0 4(1- х)=16-8х +х²

х =1 4 - 4х = 16- 8х + х²

Х² - 4х + 12 = 0

нет корней

Проверка: = 1 - верно

Ответ: 1.

9. = х + 3, возведём в куб обе части данного уравнения

5х + 27 = х³ + 9х² + 27х + 27

х(х² + 9х + 22) = 0

х = 0 х² + 9х + 22 = 0 - данное уравнение корней не имеет

Ответ: 0

10. = ОДЗ: х 4

Возведём в 6 - ую степень обе части уравнения

х² = (х - 4)³

х³- 13х² + 48 х - 64 = 0

группируем, ( х³ - 8х²) - (5х² -40х) + ( 8х - 64) = 0

х²(х - 8) - 5х(х - 8) + 8(х -8) = 0

(х - 8)(х²- 5х + 8)= 0

х - 8 = 0 х²- 5х + 8 = 0- данное уравнение корней не имеет

х = 8

Проверка: =

2= 2 верно

Ответ: 8

4.При решении иррациональных кубических уравнений очень часто пользуются следующим приемом. Будем возводить в куб, но при этом пользоваться модифицированными формулами сокращенного умножения:

(а-b)³= a³ - b³- 3ab(a - b)

(a + b)³= a³ + b³ + 3ab(a +b),

тогда a-b = c, (a- b)³ = c³, a³ - b³ - 3abc = c³

a + b = c, (a+b)³ = c³, a³ -b³ + 3abc = c³

При данном методе обязательно делать проверку! При решении уравнений данным методом появляются посторонние корни!

Пример:

+ = ОДЗ: х 0

Возведём в куб обе части уравнения, получим:

54 + + 3 ·( + )+ 54 - = 18

108 + 3 · = 18

3 = 18 - 108

= - 30

52488- 18х = - 27000

х = 4416, проверка подтверждает, что это корень уравнения

Ответ: 4416.



2. - = 1, возведём в куб обе части данного уравнения с использованием формул, приведенных выше:

х + 25 - (х +6) - 3 · ·( - ) = 1,

но выражение - должно быть равно правой части, т.е. 1

х + 25 - х - 6 - 3 · · 1 = 1

19- 3 ·

-3 · = - 18

· = 6, теперь возведём в куб, получим обычное квадратное уравнение: х² +31х - 66 = 0 корни которого х₁= 2 х₂= - 33

Проверка: х₁ = 2 =1

3- 2=1 1=1 верно

х₂ = -33 - = 1

-2 +3 = 1 1=1 верно

Ответ: - 33; 2



3. + = , возведём обе части уравнения в куб, получим :

х - 1 + 2х - 1 + 3· · ·( + = 3х + 1, учитывая, что выражение в скобках равно , получим уравнение:

3 · · = 3

· · = 1 , возведём обе части данного уравнения в куб

(2х²- х - 2х + 1)·( 3х +1) = 1

6х³ + 2х² - 9х² - 3х + 3х + 1 = 1

6х³- 7х² = 0

х²(6х - 7) = 0

х²= 0 6х - 7 = 0

х = 0 х=

Проверка показывает х =0 - посторонний корень.

Ответ:

Решить уравнения:

1. = - 1

2. = 4

3. - = 1

4. - = 2

5. - = 2

6. - = 1

7. - = 1

8. - = 1

9. + = 2

10. + = 5

11. = 2-

12. + = 4

13. + = 8

5. При решении иррациональных уравнений также применяется метод сведения к системе уравнений.

Пример

- = 1



= а a³= x + 34 a³-b³ = 37 ( a- b)( a² = ab + b²)= 37

⇔ b³ = x -3 ⇔ a - b = 1 ⇔ a- b = 1

a - b = 1 a - b = 1



a² + ab + b² = 37 a = b + 1 a= b + 1

a= b + 1 ⇔ 3b² + 3b - 36 = 0 ⇔ b² + b - 12 = 0

a = b + 1 a= b + 1 1) = 3 2) = - 4

b₁= 3 b₂ = - 4 х =30 х = - 61

Ответ: -61; 30

Решить уравнения

1. = = 6

2. = 1 -

3. - = 1

4. - = 1

5. - = 3

6. + = 2

7. + = 3

8 . = 1 -

6. Решение иррациональных уравнений методом введения новой переменной.

Пример:

1. + = 20, введём замену =а а 0, уравнение примет вид:

а² + а - 20 = 0

а₁ = 4 а₂ = - 5- посторонний корень, т.к. а 0, возвращаемся к замене

=4

х = 4⁴

х = 256

Проверка:

+ = 20

16 + 4 = 20 верно

Ответ: 256

Пример

2. 2 + 5 - 18 = 0 ОДЗ: 1- х 0

а 0

2а² + 5а - 18 = 0

а₁= 2 а₂= - 4,5- посторонний корень, т.к. а 0

данное уравнение возведём в 6-ую степень

1- х = 64

х = - 63, входит в ОДЗ

Ответ:- 63

Пример

3. = 5 -

= а

= 5- а ОДЗ: 5 - а 0

а + 1 = 25 - 10 а + а²

а² - 10 а + 25 - а - 1= 0

а² - 11а + 24 = 0

а₁ = 3 а₂ = 8- посторонний корень, т.к. а

= 3, возведём в куб обе части данного уравнения

2х - 7 = 27

2х = 34

х = 17

Проверка:

= 5 -

=5- 3

2 = 2 верно

Ответ: 17

Решить уравнения:

1. 2 = 3 -

2. 9 - 8 - = 0

3. + - 6 = 0

4. - 3 = 2

5. 2 - = 6

6. - 2 = 3

7. - = 56

8. Х + - 3 = 0

Пример

4. Х² + = 22

х² + 20 - 20 + = 22

х² + 20 + =42

= а а 0

а² + а = 42

а₁= - 7- посторонний корень , т.к. а а₂= 6

=6

х² + 20 = 36

х² = 16

х₁ = 4 х₂ = - 4, проверка показывает, что числа -4 и 4 являются корнями данного уравнения

Ответ:-4; 4

Решить уравнения:

1. Х² + 11 + = 42

2. Х² + = 12 - 2х

3. Х² - 3х = 5

4. (х -3)² + 3х - 22 =

5. (х+4)(х+1)- 3 = 6

6. = 7 + 2х - х²

7. 10х² + 12х + 12 = 5

8. 3х² + 15х + 2 = 2

Пример

5. 4 - 5 = 8



= а а

4а - = 8

4а² - 5 - 8а = 0

а ≠0

а₁ = 2, 5 а₂ = - 0,5 - посторонний корень, т.к. а

= 2,5

= 6,25

5х + 4 = 18,75 - 12,5

3х - 2 ≠ 0

13,75х= 16,5

х = 1,2 Проверка показывает, что число 1,2 корень исходного уравнения

Ответ: 1,2

Решить уравнения:

1. + = 2

2. + = 2

3. +

4. - =

5. - = 1

6. - =

7. + = 5

8. - 2 =

Пример

6. + = 2 ОДЗ: 2 - х 0

= а а0

а + = 2

а² + 3а + 4 = 2а + 6

а + 3 ≠ 0



а² + а- 2 = 0

а₁= 1 а₂ = - 2 - посторонний корень, т. к. а0

= 1

2 - х = 1

- х = 1 -2

х = 1

Проверка показывает, что х = 1 корень исходного уравнения

Ответ: 1

Решить уравнения:

1. - = 2

2. + 2

3. 1 + = 2

4. = +

5. - = 2

6. 2 - - 7 = 0

7. - 2 = 3

Пример

7. + =

+ =

Введём новую переменную х² + х + 1 = а, уравнение примет вид

+ =

ОДЗ: а

2а + 7

а + 3



= -

а + 3 = 2а + 7 + а - 2

2 = 2а + 4

= а + 2

2а² + 7а = а² + 4а + 4

а² + 3а - 4 = 0

а₁ = 1 а₂ = - 4- посторонний корень, т.к. а

Возвращаемся к замене,

х² + х + 1= 1

х(х + 1) = 0

х₁ = 0 х₂ = -1

Проверка:

Проверка показывает, что числа 0 и - 1- корни данного уравнения

Ответ: - 1; 0

Решить уравнение

1. 2х² + 3х + = 33

2. Х² - 3х = 2

3. 12х² - 12х - 12 + 135 = 0

4. Х² - 5х - 3 =

Пример

8. + = 11

= а а

2х + 3 = а²

х = - После замены переменной уравнение примет вид:

+ = 11

+ = 11

+ = 11

· + · = 11



·(а+ 1) + ·( а + 3) = 11

а + 1 + а + 3 = 22

2а + 4 = 22

2а = 18

а = 9, возвращаемся к замене:

= 9

2х + 3 = 81

х = 39

Проверка:

+ = + = 5 + 6 = 11

Ответ: 39

Решить уравнения

1. + = 7

2. + = 17

3. + = 5

Пример

9. 2х² + ( 2х + 1) = 1 ОДЗ: х² - х + 1

2х² + 2х· + - 1 = 0

х² + х² + 2х · + х - х + 1 - 1 - 1 + = 0

(х² + 2х · + х² - х +1) + х - 2 + = 0

(х + )² + х + - 2 = 0

Введём новую переменную: х + = а, уравнение примет вид:

а² + а - 2 = 0

а₁ = 1 а₂ = -4, возвращаемся к замене, получаем два уравнения с переменной х:

х + = 1 х + = - 4

= 1-х = -4 - х

ОДЗ: х² - х + 1 ОДЗ: х² - х + 1

1- х - 4 - х

х² - х +1=(1-х)² х² - х + 1= (-4-х)²

х² - х + 1= 1 - 2х + х² х² - х + 1 = 16 - 8х +х²

х²- х + 2х - х² = 1- 1 х² - х +8х -х² = 16 - 1

х = 0 х = 2 не входит в область допустимых

значений.

Ответ: 0

Пример

10. Тригонометрические подстановки

Иногда при решении иррациональных уравнений удобно использовать тригонометрические подстановки ( их следует применять, если структура данного иррационального уравнения напоминает какую- то тригонометрическую формулу:

- если в уравнение входит , то полагаем х = а· sint или x= a·cost

- если входит , то х = а ·tgt

- если входит , то х = или х = .

Решить уравнение:

1. + х = 1

Пусть х = 2· sint, t, на отрезке поэтому

=

Наше уравнение примет вид:

+

2

=

, тогда



t+ + , n

t = - arcsin + + , n,

учитывая, что t получим два корня:

t₁ = - arcsin

t₂= - arcsin

x₁=2sint₁ = 2 sin( - arcsin)·cos(arcsin arcsin - · ) =

2·(0,2 -0,8)= - 1,2

x₂= 2 sin(t₂) = 2 sin( +arcsin 2(0,2 + 0,8) = 2

Ответ: - 1,2; 2

2. 2х + 2х² - 1 = ОДЗ: -1

х = cost

2sint ·cost + 2 - - =

sin2t + cos2t =

+ + 2 sin2t ·cos2t = 1,5

2sin2t·cos2t + 1= 1,5

sin4t = 0,5

4t =

t =

x = cos

Ответ: cos

3. Х + = (2х² - 1) ОДЗ: х

Выполним замену: х = cost, 0 ( согласно ОДЗ)

cost +

т.к. 0 ,

cost +

(cost +

(cost +

tgt = - 1

t= -

t = т.к. 0

t= t= , возвращаемся к подстановке

х₁ = cos = - х₂ = cos

Ответ: х₁ = cos = - ;х₂ = cos

Решить уравнения:

1.

2.

3. Х +

4. 16х(2х² + 1)5.



В некоторых случаях тригонометрические подстановки - наиболее простой способ решения уравнений. При его использовании нужно помнить, что алгебраическое уравнение должно иметь ответ, записанный алгебраически

( без тригонометрических функций)



7. Метод разложения на множители выражений, входящих в уравнение.

Пример

1. (х +3) = 3 ОДЗ: х - 1

х² - 1

(х +3) - 3· = 0

(х+3 - 3) = 0

= 0 х+3 - 3 = 0

х -1 = 0 - 3 = -х - 3

х - 1 из области ОДЗ 3 = х+3 ОДЗ: х+3

х+ 1

9(х+1) = х² + 6х + 9

9х + 9 = х² + 6х + 9

х² - 3х = 0

Х(х- 3)= 0

х= 3 х = 0-посторонний корень

Ответ:1; 3

Решить уравнения:

1. (х+1) · = 2х + 2

2. Х · = 18х² - 17 х

3. 9 - х² = 0

4. =

Пример

2. 2- 3х +х² = 2(х -1) , ОДЗ: х , в левой части квадратный трёхчлен разложим на множители:

(Х-1)(х-2) =2(х-1)

(х-1)(

х - 1= 0 0

х = 1 = а, а

а² -2а -2 = 0

а₁= 1+ а₂ = 1- - посторонний корень

= 1+

х = 4 + 2

Ответ:1; 4 + 2

Пример

3. + - - = 0

Если внимательно посмотреть на уравнение, то можно увидеть, что разности подкоренных выражений первого и третьего, а также второго и четвёртого членов этого уравнения равны одной и той же величине(-2х - 4). В этом случае воспользуемся тождеством: - = , а> 0, у > 0, а + у > 0, уравнение примет вид:

+ = 0

(2х + 4)( + )= 0

2х + 4 = 0

Х = - 2

+ = 0 - данное уравнение не имеет решений, т.к. его левая часть положительна в своей области определения





2х²- 1>0

2х² + 2х + 3 >0

х² - х +2 >0

х² - 3х - 2> 0

Проверка х = -2

+ - - = 0

Ответ: -2

Пример

4. Решение уравнений методом разложения подкоренного выражения на множители

- =

2х² + 5х + 2 = 0 х² + х - 2 = 0

х₁ = -2 х₂ = - х₁ = 1 х₂= -2

2х² + 5х + 2= 2(х + 2)(х+ ) х² + х - 2= (х+2)(х-1)

- =

ОДЗ: 2х² + 5х + 2

х² + х - 2

3х + 6

- - = 0

· - - ) = 0

= 0 - - = 0

х = - 2 = +

2х+ 1= х - 1 + 3 + 2

2 = х - 1 ОДЗ: х - 1

4(3х - 3)= х² - 2х + 1

х² - 14х + 13= 0

х₁= 13 х₂ = 1 Проверка показывает, что посторонних корней нет.

Ответ: -2; 1; 13

Решить уравнения:

1. + =

2. + =

3. - =

4. + =

5. - =

6. - =

7. - =

8. - =

8. Решение уравнений методом умножения на сопряжённые выражения.

В некоторых случаях можно освободиться от иррациональности в уравнении умножением обеих частей уравнения на некоторое не обращающееся в нуль выражение.

Пример

- = 2Х (1)

ОДЗ: 2х² + 8х + 7

2х² - 8х + 7

Умножим обе части уравнения на + , являющееся сопряжённым к левой части данного уравнения, получим

2х² + 8х + 7 -2х² + 16х - 7= 2х( + )

16х = 2х( + ) - данное уравнение эквивалентно исходному.

х = 0 или + = 8

Сложим уравнение + = 8 с (1), получим

2 = 2х + 8

= х +4 ОДЗ: х + 4

2х² + 8х + 7 = (х+ 4)²

2х² + 8х + 7 = х² + 8х + 16

х²= 9

х =

х = - 3 х = 3

Получили корни: х = - 3 ; х = 3; х = 0- все они из области допустимых значений

Ответ: -3; 0; 3

Решить уравнения:

1). + = 7

2). - = 1

3). = 3

4). - = 1

5). = 2

6). - = 2Х

7). + = 8Х

8). + = 3Х

9). - = 1

9. Решение уравнений методом выделения полного квадрата в подкоренном выражении.

При решении некоторых иррациональных уравнений применяется формула

=

Пример

1. - =

- =

Введём замену = а, а , уравнение примет вид:

- = а

а + 1- = а

= 1

а - 2 = 1 а - 2 = - 1

а = 3 а = 1, возвращаемся к замене

1) = 3 2) = 1

х + 4 = 9 х + 4 = 1

х = 5 х = - 3

Проверка: - =

- =3

4- 1 = 3

2) - =

- = 1

2 - 1 = 1

Ответ: -3; 5

Решить уравнения:

1). + = х - 1

2). + = 4

3). + = 6

4). + = 5

5). + =

6). + =

7). + =7

8). + =

10. Решение уравнений методом оценки.

Этот способ применим в том случае, когда подкоренные выражения представляют собой квадратный трехчлен, не раскладывающийся на линейные множители. Поэтому полезно оценить левую и правую части уравнения.

Пример

1. + = 4 - 2х - х²

ОДЗ: 4х² + 8х + 8

3х² + 6х + 12

4 - 2х - х²

Оценим обе части уравнения:

= = 2

= = 3

4 - 2х - х² = - (х² + 2х - 4) = - ((х + 1)²- 5)= 5 - (х+1)² 5.

Левая часть уравнения существует при всех значениях переменных х, не меньше 5, а правая при всех значениях , не больших 5, следовательно, уравнение будет иметь решение, если обе части уравнения одновременно равны 5, т. е. справедлива следующая система:

+ = 5

4 - 2х - х² = 5

4 - 2х - х² = 5

х² + 2х - 4 + 5 = 0

х² + 2х + 1 = 0

(х+ 1)² = 0

х = - 1

Проверим, является ли это число корнем уравнения

+ = 5

+ = + = 2 + 3 = 5

Ответ: -1



2. Х² + 2 + = 2х +

= = 4

х² - 2х + 2 + = 4 (Применили неравенство Коши: х + у )

Равенство верно при х = 0 и х =2

Проверка

х = 0

0² + 2 + = 2·0 +



2 + 2=

4≠, х = 0 - посторонний корень

х = 2

4+ 2 + = 4 +

6+ 2 = 4+ 4

8 = 8, х =2 - корень исходного уравнения

Ответ:2

3. + = 2 - х²,

т.к. для любых значений х, то левая часть уравнения не меньше 2 для любых значений х.

Правая часть 2 - х² 2 для любых значений х. Поэтому уравнение может иметь корнями только те значения х, при которых

+ = 2

2 - х² = 2

Решая уравнение 2 - х² = 2, найдём х = 0, Это значение удовлетворяет и первому уравнению системы, х = 0 - корень исходного уравнения

Ответ: 0

Решить уравнения:

1) + = 3 - 5х²

2) + = 3

3) + = 3

4) + + = 5

11 метод . Использование монотонности функций.

Прежде чем использовать данный метод обратимся к теории.

Нам понадобятся следующие свойства:

Если функции y=f(x) и y=g(x) возрастают (убывают) на некотором множестве, то функция y=f(x)+g(x) также возрастает (убывает ) на этом множестве.

Если функции y=f(x) и y=g(x) возрастают (убывают) на некотором множестве, при чем обе они принимают неотрицательные значения при всех допустимых х, то функция y=f(x)g(x) возрастает (убывает) на данном множестве.

Если функция y=f(x) монотонная, то уравнение f(x)=a имеет не более одного решения.

Если функции y=f(x) и y=g(x) имеют разный характер монотонности, то уравнение f(x)=g(x) имеет не более одного решения.

Функция вида возрастает при к>0 и убывает при к<0.

Пример

1). = 6 -

Один корень данного уравнения х= 2 легко найти подбором. Покажем, что других корней нет. Запишем уравнение в виде:

+ = 6 ОДЗ: х + 6

По свойству степенных функций у₁ = и у₂ = являются возрастающими на промежутке , где они обе определены. Поэтому их сумма у = + тоже возрастает на этом промежутке, следовательно, она принимает каждое свое значение( в том числе и 6) только один раз. Поэтому других корней нет.

Ответ:2.

2). + = 9 -

Это уравнение можно попытаться решить возведением в квадрат трижды. При этом получиться уравнение четвёртой степени. Попробуем найти корень подбором, х = 1

Левая часть уравнения- возрастающая функция, а правая - убывающая функция. Это значит, что больше одного корня такое уравнение иметь не может.

Ответ: 1

3) х² + х+ 12 = 36 ОДЗ:

Подбором определяем, что х = 3.

Но левая часть уравнения не задает монотонную функцию. Но на (0; + указанная функция возрастает, при чём корень х = 3 принадлежит этому промежутку. Значит на ( 0; + данное уравнение имеет единственный корень.

Исследуем функцию у = х² + х+ 12 на отрезке .

При х х² + х , а 12 , следовательно, при х исходное уравнение корней не имеет.

Ответ: 3

Решить уравнения:

1) + + = 10

2) + 2 + = 8

3) х + + + х² = 10

4) + = 8

5) + = 2

6) + =

7) + = 6

8) + х - 2 = 0

9) 3 + 4 + 5 =

12. Полезно при решении иррациональных уравнений начинать с ОДЗ.

Пример:

1. + + = 0

Данное уравнение имеет громоздкий вид и неясно как подойти к его решению. Поэтому сначала найдём ОДЗ

х³ + - х(х² + - ) 0

х - 6 0 х 6

13х - 2х³- х² - 6 0 2х³ + х² - 13х + 6 0

х(х+ 5)(х - ) 0 х ; +

х 6 х ; +

(х-2)(2х² + 5х - 3) х ;

х . Получили, что область допустимых значений данного уравнения является пустым множеством, следовательно, данное уравнение корней не имеет

Ответ: нет корней.

2. + = 3

ОДЗ: 3-х 0

х - 5 0

ОДЗ данного уравнения является пустым множеством, следовательно, данное уравнение корней не имеет

Ответ: нет корней

3.

ОДЗ:



х² - 12

Поскольку х = 4 есть единственное допустимое значение, достаточно проверить, является ли оно решением уравнения. Подставив х = 4 в уравнение получим верное числовое равенство 0 = 0, следовательно х = 4 единственный корень данного уравнения

Ответ: 4

Решить уравнения:

1. - = -

2. )

3. = 2 - х

4. = х²- 7х + 12

5. = х² - 4х + 6 ОДЗ : . Правая часть уравнения принимает минимальное значение 2 при х = 2, а левая часть уравнения принимает максимальное значение 2 при х = 2, следовательно, х = 2 - корень уравнения.

Ответ : 2

6.

7. =х²

8.

9. = х² + 3

10. = 2006

11. = х² - х + 2

12.

13.

13. Графический способ решения иррациональных уравнений.

Пример

1. = 3х - 2

Построим графики функций у= и у = 3х - 2

Ответ: 1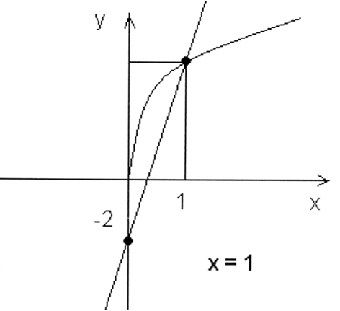

2.

Построим графики функций у = и у =

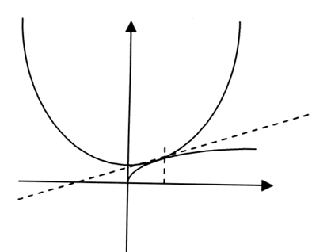х = 1 - корень уравнения, но утверждать, что это единственный корень, мы пока не можем, поскольку функции у = и у =

возрастают в области определения уравнения, т. е. на луче .

Найдём производные функций и вычислим их значения в т. х = 1( в точке пересечения графиков этих функций)

у^, = у^,(1) = у^, = у^,(1) =

Т.к. производные данных функций при х = 1 принимают равные значения, то графики функций у = и у = имеют общую касательную в точке (1;1) . Поскольку функция у = выпукла вниз, а функция

у = выпукла вверх, то их графики расположены по разные стороны от общей касательной, а поэтому уравнение имеет только один корень, х = 1.

Ответ: 1

3. = -х² + 14х - 46

Строим графики функций у = и у=-х² + 14х - 46



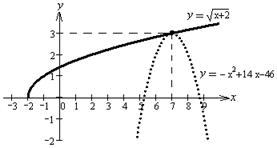
Из рисунка видно, что графики пересекаются в единственной точке х = 7, Следовательно уравнение имеет единственное решение . Проверяем х = 7 подстановкой в заданное уравнение и убеждаемся, что это точное значение уравнения = - 49 + 14·7 - 46 3= 98 - 95 3=3

Ответ: 7

4. + = - Рассмотрим функции у= и у = -

Функция у= возрастает при х Функция у = - убывает при х . Построим графики данных функций в одной системе координат.

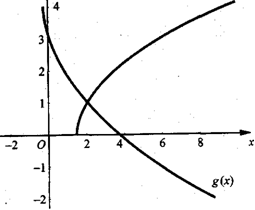
Графики функций пересекаются в точке с абсциссой х = 2, т. к. функция

у= возрастает, функция у = - убывает, то данное уравнение имеет единственный корень х = 2

Ответ : 2

5. 1- х² =

Рассмотрим две функции у= 1- х² и у= троим графики функций в одной

системе координат

Ответ: х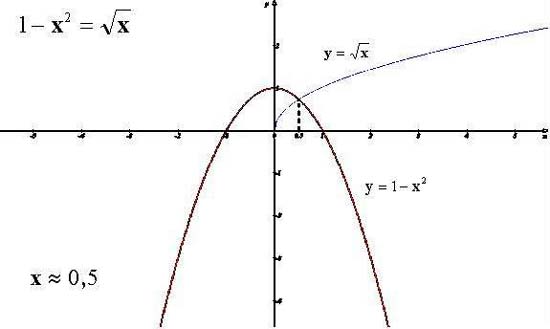

Т.к. графический способ даёт не точные значения переменной, то его применяют при решении иррациональных уравнений реже.

Литература:

1. «Математика 10 - 11 классы. Уравнения и неравенства. Приёмы, методы, решения» Составитель Е.В. Мрошкина, Волгоград. Издательство «Учитель»

2. «Математика. Тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов» Составители: Г.И. Ковалёва, Т.И. Бузулина, О.Л. Безрукова, Ю.А. Розка. Волгоград. Издательство «Учитель» 2009

3. Повторение и контроль знаний. Математика 9- 11 классы. Подготовка к ГИА и ЕГЭ. Книга 1( Арифметика. Общие методы алгебры. Алгебра многочленов) Составители: Н.И. Гданский, А.В. Карпов. Москва Издательство «Планета» 2010

4. «Решение сложных задач ЕГЭ по математике» С.И. Колесникова. Москва «Вако» 2011

5. « Математика ЕГЭ . 1000 задач с ответами и решениями» Составители: И.Н. Сергеев, В.С. Панферов. Москва. Издательство «Экзамен» 2013

6.Глазков Ю.А. , Корешкова Т.А., Мирошин В.В. Шевелева Н.В. Математика. ЕГЭ.:Методическое пособие для подготовки к ЕГЭ по математике. - М.: Издательство «Экзамен», 2007.

7. Моденов П.С. Пособие по математике, Ч.1, М:, 1977.

8. Башмаков М.И. Беккер Б.М., Гольховой В.М. Сборник задач по алгебре и анализу, Библиотечка «Квант», М., 1983.

9. Ципкин А.Г., Пинский А.И. Справочное пособие по методам решения задач по математике для средней школы. М., Наука, 1983.

10. www.vevivi.ru/best/Primenenie-trigonometricheskoi-podstanovki-dlya-resheniya-algebraicheskikh-zadach-ref172041.html

</