Учителю
Урок в 6 классе на тему Координатная плоскость в жизни человека.

Урок в 6 классе на тему Координатная плоскость в жизни человека.

Автор публикации: Сысоева А.Н.

Дата публикации: 27.04.2015

Краткое описание: Тема урока «Координатная плоскость в жизни человека».Цели: Закрепить навык нахождения координат точек и построения точек по их координатам; Показать практическое значение координатной плоскости в жизни человека; Научить обрабатывать и обобщать полученную в результате

предварительный просмотр материала

Урок математики в 6 классе

Тема урока «Координатная плоскость в жизни человека».

Цели:

Закрепить навык нахождения координат точек и построения точек по их координатам;
Показать практическое значение координатной плоскости в жизни человека;
Научить обрабатывать и обобщать полученную в результате исследования информацию.
Формировать навыки работы в сфере самостоятельной познавательной деятельности, навыки работы в команде.
Воспитывать ответвенность за порученное дело.
Воспитывать внимательность, аккуратность при выполнении построений

Оборудование:

Компьютер, медиапроектор, карточки с заданиями, выставка работ учащихся, CD « Мир информатики», 3 класс, «Координаты», презентация учащихся «Координаты вокруг нас», публикация учащихся «Кто и когда придумал систему коодинат».

План урока.

Организационный момент.
Вступительное слово учителя.
Разминка: Устный счет.
Сведения из истории. Представление буклета учащегося.
Практическая работа групп учащихся: а) рисунки в координатной плоскости, б) упражнение с компьютерной программой «Мир информатики». В) определение координат точек.
Физкультминутка.
Представление презентации учащихся «Координатная плоскость в нашей жизни».
Координатные загадки.
Итог урока.
Задание на дом.

Конспект урока.

I Оргмомент.

Здравствуйте, дети и гости.

Тема нашего урока «Координатная плоскость в жизни человека».

Задачи урока:

Закрепить навык нахождения координат точек и построения точек по их координатам;

Показать практическое значение координатной плоскости в жизни человека;

Научиться обобщать и представлять полученную в результате исследования информацию.

I I Вступительное слово учителя.

Мы часто слышим слова « Оставьте мне свои координаты». Это выражение означает, что собеседник должен оставить свой адрес или номер телефона.

Итак, координаты - это место расположения того или иного объекта.

На уроке мы познакомимся с работами учащихся нашего класса.

Фронтальный опрос

Закончить фразу:

Координатной плоскостью называется плоскость, на которой…
Систему координат образуют…
Области, на которые оси разбивают координатную плоскость, называют…
Координатная прямая ОХ называется…
Координатная прямая ОY называется…
Первая координата точки называется…
Вторая координата точки называется…
Если абсцисса точки равна нулю, то точка лежит…
Если ордината точки равна нулю, то точка лежит…
Если обе координаты точки равны нулю, то точка лежит…

I I I Разминка.

Выполнив вычисления вы узнаете координаты точек фигуры. (Написать на доске)

Название точки

Координаты точки

-4-2

-8,5+6,5

-20:(-10)

0:10,02

-10+16

31,7-29,7

-11,2+11,2

2,8:(-1,4)

-5-(-5)

-1,02+(-0,98)

Ответы: A(-6;0); B(-2;2); C(0;6); D(2;2); E(6;0); F(2;-2); G(0;-6); H(-2;2).

IV Сведения из истории.

Представление буклета учащихся.

Когда мы начали изучать тему «координатная плоскость», то заинтересовались вопросом «Когда и кто придумал систему координат?». Всё, что мы узнали, оформили в виде буклета.

Первоначально идея координат зародилась в древности в связи с потребностями астрономии, географии, живописи. Древнегреческий астроном Клавдий Птолемей(IIв.) применил географические координаты( долготу и широту) для определения местонахождения мореплавателей. Идеей координат пользовались в средние века для определения положения светил на небе, для определения места на поверхности Земли. Прямоугольной сеткой пользовались художники эпохи Возрождения.

Применять координаты в математике впервые стали Пьер Ферма ( 1601-1665 ) и Рене Декарт ( 1596-1650). В 1637 году вышла книга Рене Декарта Рассуждения о методе». В ней он предложил новый метод-метод координат, который позволил переходить от точки в координатной плоскости к паре чисел-её координатам.

Метод координат позволяет строить графики уравнений, изображать геометрически различные зависимости, выраженные с помощью уравнений и формул.

Термины «абсцисса» и «ордината» были введены в употребление Г. Лейбницем (1646-1716) в 70-80 годы XVII века. Термин «координаты» произошел от латинского слова «ordinates» - «упорядоченный», а приставка «co» указывает на «совместность»: координат обычно бывает две и более. «Абсцисса» (латинское слово «abscissus» -«отрезанный».

IV Весёлая ФИЗКУЛЬТМИНУТКА

Наклоны выполнять по схеме (Х,У),

где Х-вправо (положительное число), влево (отрицательное число);

У-вперёд (положительное число), назад (отрицательное число).

1)Исходное положение (0;0). Поставьте руки на пояс, ноги на ширине плеч.

2)Наклоны начинай:

(2;2), (0;0) (-2;-2), (0;0)

(3;-3), (0;0), (-3; 3), (0;0)

(-1;-2), (0;0), (2;-3), (0;0)

(2;-2), (0;0), (1;-3), (0;0)

VI Практическая работа.

1) 3 человека работают на компьютере: программа «Мир информатики», 3 класс, «Координаты»;

2) 1 человек на доске определяет координаты точек рисунка;

«Кораблик»

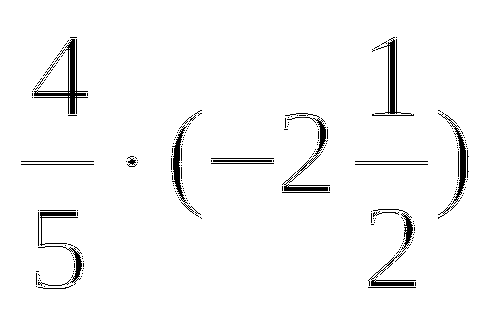
-7 -5 -3 -1 1 3 5 7 9 х

о -1

-3

-5

-7

Ответ:

(-2, 0) Парус 1-ое окно 2-ое окно 3-е окно

(-3, 1) (1, 0) (-4, -1) (-2, 0) (2, 0)

(-7, 1) (1, 6) (-3, -1) (-2, -1) (2, -1)

(-4, -2) (-2, 3) (3, 0) (-1, -1) (1, -1)

(6, -2) (1, 1) (4, 0) (-1, 0) (1, 0)

(7, 1)

(3, 1)

(2, 0)

(0, 0)

3) остальные учащиеся составляют рисунки по готовым координатам на карточках.

Задания из рабочей тетради «Математика 6» (автор Е. А. Бунимович), стр53. №129, 130.

Проверка выполненных работ.

VII Представление презентации учащихся «Координаты вокруг нас».

Суть координат состоит в следующем: это правило, по которому определяется положение того или иного объекта.

1) Системы координат пронизывают всю практическую жизнь человека.

Это почтовые адреса и номера телефонов, в поезде номер вагона и номер места, в многозтажном доме номер подъезда и номер этажа.

2) Система координат в зрительном зале (номер ряда и номер места). Пользуясь знанием координат можно составить «живые картинки». Например: «Живая картина» открытия XII Всемирного фестиваля молодёжи и студентов в Москве в 1985 году.

3)Географические координаты (долгота и широта) представлена на картах, туристических маршрутах.

4)Система координат используется в шахматах, где вертикали обозначаются цифрами, а горизонтали латинскими буквами.

5)Систем координат мы пользуемся, когда играем в « Морской бой».

6)Не обойтись без системы координат и в математике, физике, статистике, бухгалтерском деле.

В своей бытовой и профессиональной деятельности человек регулярно сталкивается с прямоугольной декартовой системой координат, имеющей огромное практическое применение.

Значение системы координат велико:

она позволяет определить положение того или иного объекта.

VIII (дополнительно) Координатные загадки:

ЗАДАНИЕ №1

«пробел»

Расшифруйте следующее сообщение с помощью таблицы:

(9;3) (1;3) (12;1) (5;3) (5;1) (2;3) (2;2) (5;1) (12;1) (5;3) (5;1) (2;3) (2;2) (5;1) (3;1) (12;1) (10;3)

(12;1) (1;2) (2;1) (1;3) (4;2) (11;1) (4;2) (12;3)

Ответ: За добро добром и платят.

Задание №2 «Кладоискатель».

Однажды дядя Федор, кот Матроскин и пес Шарик решили купить корову. Где же взять деньги? Очень просто! Искать клад!В старом сундуке нашлось зашифрованное письмо, содержащее описание пути, ведущего к кладу, и места, где он спрятан. Хозяева клада очень любили математику и для шифровки использовали метод координат. Они взяли карту деревни Простоквашино, нарисовали по ней оси координат, выбрали единицы масштаба. В качестве ориентира были указаны координаты колодца (3; 4) на краю леса, магазина (-2; -1), почты (3; 0), дома (0; 3). Клад находился в точке пересечения прямых, соединяющих дом и почту, магазин и колодец.

IX Итог урока

Ответить на вопросы: