- Учителю
- РАБОЧАЯ ПРОГРАММА по алгебре 10-11 класс
РАБОЧАЯ ПРОГРАММА по алгебре 10-11 класс
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 59
имени Героя Советского Союза Д.А.Медведева
УТВЕРЖДЕНА
Педагогическим советом МБОУ СОШ №59 протокол от «__» ___________20___ г. №
Председатель педсовета
_____________________Т.А.Дороничева
РАБОЧАЯ ПРОГРАММА
по алгебре
10-11 класс
III ступень обучения
Разработала учитель математики
первой квалификационной категории
Рогова Н.Н.
г.Узловая 2014
Пояснительная записка
Рабочая программа по алгебре и началам анализа для 10-11 классов старшей школы составлена на основе:
- федерального компонента государственного образования среднего (полного) общего образования;
- примерной программы по математике среднего (полного) общего образования базовый уровень;
- программы по алгебре и началам математического анализа 10-11 класс авторов С.М. Никольского, М.К. Потапова и др., /Программы общеобразовательных учреждений. Алгебра и начала математического анализа. 10-11 классы. Составитель Т.А. Бурмистрова. - М.: Просвещение, 2010/
- федерального перечня учебников, рекомендованных Министерством образования Российской Федерации;
- учебного плана муниципального бюджетного общеобразовательного учреждения средней общеобразовательной школы № 59 на 2014-15 учебный год.
Алгебра и начала анализа в 10-11 классах изучается в рамках базового уровня, предназначенного для учащихся, выбравших те области деятельности, в которых математика играет роль аппарата, специфического средства для изучения закономерностей окружающего мира.
Целью курса является систематическое изучение функций, как важнейшего математического объекта средствами алгебры и математического анализа, раскрытие политехнического и прикладного значения общих методов математики, связанных с исследованием функций, подготовка необходимого аппарата для изучения геометрии и физики.
Изучение математики на базовом уровне среднего (полного) общего образования направлено также на достижение следующих целей:
-
овладение системой математических знаний и умений, необходимых в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
-
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также для последующего обучения в высшей школе;
-
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
-
воспитание средствами математики культуры личности, понимания значимости для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики.
Место предмета в учебном плане
Согласно учебному плану школы обучение алгебре и началам анализа ведется в объеме 210 часов: 105 часов в год - в 10 классе и 105 часов в год в 11 классе.
Предмет
Количество часов в неделю в 10 классе
Количество часов в неделю в 11 классе
Алгебра и начала анализа
3
3
В том числе: контрольных работ в 10 классе - 7, в 11 классе - 7, включая итоговую контрольную работу.
Формы промежуточной и итоговой аттестации
Промежуточная аттестация проводится в форме тестов, контрольных, самостоятельных и диагностических работ. Итоговая аттестация - в виде итоговой контрольной работы в 10 классе и государственной итоговой аттестации в виде единого государственного экзамена в 11 классе.
В авторскую программу внесены следующие изменения: в 10 классе увеличено на 3 количество часов на изучение темы «Показательные и логарифмические уравнения и неравенства» ввиду ее достаточной сложности и важности прочного усвоения для успешного прохождения учащимися итоговой аттестации. Из тех же соображений на 2 часа больше, чем предусмотрено программой, запланировано на изучение темы «Тригонометрические уравнения и неравенства», а также на 1 час больше на изучение темы «Элементы комбинаторики, статистики и теории вероятностей». В результате вышеуказанных изменений на итоговое повторение запланировано 8 часов, а не 10 как в программе.
В 11 классе целесообразно вместо 6 часов взять 8 на изучение темы «Функции и графики», так как учащиеся должны получить прочные навыки преобразования графиков функций и исследования функций элементарными методами, что достаточно сложно. Также планирую дополнительно 2 часа на знакомство с некоторыми приемами решения уравнений и неравенств с параметрами. За счет более компактного изучения тем «Уравнения-следствия» и «Равносильность уравнений и неравенств системам» возможно 2 часа добавить на изучение темы «Уравнения и неравенства, равносильные на множествах». В результате всех этих изменений на итоговое повторение остается 13 часов вместо 15 по программе, что можно компенсировать текущим повторением в течение учебного года.
Перечень разделов программы (тем)
10 класс
Темы
Количество часов
Действительные числа.
7
Рациональные уравнения и неравенства.
14
Корень степени n.
8
Степень положительного числа.
9
Логарифмы.
6
Показательные и логарифмические уравнения и неравенства.
10
Синус и косинус угла.
6
Тангенс и котангенс угла.
4
Формулы сложения.
9
Тригонометрические функции числового аргумента.
8
Тригонометрические уравнения и неравенства.
10
Элементы комбинаторики, статистики и теории вероятности.
5
Повторение.
8
Контрольных работ-7
11 класс
Темы
Количество часов
Функции и их графики.
9
Предел функции и непрерывности.
5
Обратные функции.
3
Производная.
9
Применение производной.
15
Первообразная и интеграл.
11
Уравнения-следствия.
6
Равносильность уравнений и неравенств. Равносильность уравнений и неравенств системам.
11
Равносильность уравнений и неравенств на множествах.
9
Метод промежутков для уравнений и неравенств.
4
Системы уравнений с несколькими неизвестными.
7
Уравнения и неравенства с параметрами.
3
Повторение.
10
Контрольных работ-7
Содержание обучения
10 класс
-
Действительные числа (7 ч)
Понятие действительного числа. Множества чисел. Свойства действительных чисел. Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач.
-
Рациональные уравнения и неравенства (14 ч)
Рациональные выражения. Формула бинома Ньютона. Свойства биноминальных коэффициентов. Треугольник Паскаля. Формулы суммы и разности степеней. Рациональные уравнения. Решение рациональных уравнений. Системы рациональных уравнений. Решение простейших систем уравнений с двумя неизвестными. Метод интервалов решения неравенств. Рациональные неравенства. Решение рациональных неравенств. Нестрогие неравенства. Решение систем неравенств с одной переменной.
Контрольная работа № 1 по теме «Рациональные выражения, уравнения и неравенства»
-
Корень степени n (8 ч)
Понятие функции и ее графика. Степенная функция с натуральным показателем, ее свойства и график. Корень степени n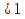 и его свойства. Корни четной и нечетной степеней. Арифметический корень. Свойства корней степени n. Функция у =
и его свойства. Корни четной и нечетной степеней. Арифметический корень. Свойства корней степени n. Функция у = 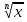 .
.
-
Степень положительного числа (9 ч)
Степень с рациональным показателем и ее свойства. Понятие предела последовательности. Существование предела монотонной ограниченной последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая прогрессия и ее сумма. Число е. Понятие степени с иррациональным показателем. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Показательная функция (экспонента), ее свойства и график.
Контрольная работа № 2 по теме «Корень степени n и степень положительного числа»
-
Логарифмы (6 ч)
Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов. Логарифм произведения, частного, степени. Переход к новому основанию. Десятичный и натуральный логарифмы. Логарифмическая функция, ее свойства и график. Степенная функция с натуральным показателем, ее свойства и график.
-
Показательные и логарифмические уравнения и неравенства (10 ч)
Решение простейших показательных и логарифмических уравнений. Уравнения, сводящиеся к простейшим заменой неизвестного. Решение простейших показательных и логарифмических неравенств. Неравенства, сводящиеся к простейшим заменой неизвестного.
Контрольная работа № 3 по теме «Показательные и логарифмические уравнения и неравенства»
-
Синус и косинус угла ( 7 ч)
Понятие угла и его меры. Радианная мера угла. Синус и косинус произвольного угла. Основные тригонометрические тождества для синуса и косинуса. Формулы приведения. Преобразование простейших тригонометрических выражений, содержащих синус и косинус. Арксинус и арккосинус числа.
-
Тангенс и котангенс угла (4 ч)
Тангенс и котангенс произвольного угла. Основные тригонометрические тождества и формулы приведения для тангенса и котангенса. Преобразование простейших тригонометрических выражений. Арктангенс и арккотангенс числа.
Контрольная работа № 4 по теме «Синус, косинус, тангенс и котангенс угла»
-
Формулы сложения (9 ч)
Косинус суммы (разности) двух углов. Формулы для дополнительных углов. Синус суммы (разности) двух углов. Тангенс суммы и разности двух углов. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Синус и косинус двойного угла. Формулы половинного угла. Выражение тригонометрических функций через тангенс половинного аргумента.
-
Тригонометрические функции числового аргумента (8 ч)
Синус, косинус, тангенс и котангенс числа. Тригонометрические функции у = sin х, у = cos х, у = tg х, у = ctg х, их свойства и графики. Периодичность, основной период.
Контрольная работа № 5 по теме «Формулы сложения. Тригонометрические функции числового аргумента»
-
Тригонометрические уравнения и неравенства (10 ч)
Простейшие тригонометрические уравнения. Решения тригонометрических уравнений. Тригонометрические уравнения, сводящиеся к простейшим заменой неизвестного. Применение основных тригонометрических формул для решения уравнений. Однородные уравнения. Простейшие тригонометрические неравенства.
Контрольная работа № 6 по теме «Тригонометрические уравнения»
-
Элементы комбинаторики, статистики и теории вероятностей (5 ч)
Табличное и графическое представление рядов данных. Числовые характеристики рядов данных. Элементарные и сложные события. Понятие и свойства вероятности события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Условная вероятность. Решение практических задач с применением вероятностных методов.
-
Повторение (8 ч)
Преобразования простейших выражений, включающих арифметические операции, а также операцию возведения в степень и операцию логарифмирования. Решение показательных, логарифмических, тригонометрических уравнений и неравенств.
Итоговая контрольная работа № 7
11 класс
-
Функции и их графики (8 ч)
Элементарные функции. Область определения и множество значений функции. Ограниченность функции. Свойства функций: монотонность, четность и нечетность, периодичность. Промежутки возрастания и убывания, сохранение знака, нули функции. График функции. Исследование функций элементарными методами. Построение графиков функций, заданных различными способами. Примеры функциональных зависимостей в реальных процессах и явлениях. Преобразования графиков: параллельный перенос, симметрия относительно начала координат, относительно осей координат, относительно прямой у = х, растяжение и сжатие вдоль осей координат. Графики функций, содержащих модули.
-
Предел функции и непрерывность ( 4 ч)
Понятие предела функции. Односторонние пределы, свойства пределов. Понятие о непрерывности функции. Непрерывность функции в точке, на интервале, отрезке. Непрерывность элементарных функций.
-
Обратные функции (3 ч)
Понятие обратной функции. Область определения и область значений обратной функции. График обратной функции. Взаимно обратные функции.
Контрольная работа № 1 по теме «Функции и графики»
-
Производная (11 ч)
Понятие о производной функции. Производные суммы, разности, произведения и частного двух функций. Производные основных элементарных функций. Производная сложной функции. Производные обратной функции и композиции данной функции с линейной.
Контрольная работа № 2 по теме «Производная»
-
Применение производной (15 ч)
Точки экстремума (локального максимума и минимума) функции, наибольшее и наименьшее значения, графическая интерпретация. Нахождение скорости для процесса, заданного формулой или графиком. Уравнение касательной к графику функции. Физический и геометрический смысл производной. Приближенные вычисления. Возрастание и убывание функции. Производные высших порядков. Вторая производная и ее физический смысл. Задачи на максимум и минимум. Асимптоты. Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций. Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических задачах. Применение производной к исследованию функций и построению графиков.
Контрольная работа № 3 по теме «Применение производной»
-
Первообразная и интеграл (11 ч)
Первообразная. Понятие об определенном интеграле как площади криволинейной трапеции. Формула Ньютона-Лейбница. Свойства определенных интегралов. Примеры применения интеграла в физике и геометрии.
Контрольная работа № 4 по теме «Первообразная и интеграл»
-
Уравнения-следствия (6 ч)
Понятие уравнения-следствия. Возведение уравнения в четную степень. Потенцирование логарифмических уравнений. Приведение подобных членов уравнения. Освобождение уравнения от знаменателя. Другие преобразования, приводящие к уравнению-следствию.
8. Равносильность уравнений на множествах ( 7 ч)
Равносильность уравнений на множествах. Равносильные преобразования уравнений. Решение рациональных, показательных, логарифмических уравнений. Решение иррациональных уравнений. Возведение уравнения в четную степень. Умножение уравнения на функцию. Логарифмирование и потенцирование уравнений, приведение подобных членов, применение некоторых формул. Применение нескольких преобразований.
Контрольная работа № 5 по теме «Решение уравнений»
-
Равносильность неравенств на множествах (6 ч)
Равносильность неравенств на множествах. Равносильные преобразования неравенств. Возведение неравенств в натуральную степень. Решение иррациональных неравенств. Потенцирование и логарифмирование неравенств. Умножение неравенства на функцию. Другие преобразования неравенств. Применение нескольких преобразований.
Нестрогие неравенства.
-
Метод промежутков для решения уравнений и неравенств (4 ч)
Уравнения и неравенства с модулями. Метод интервалов для непрерывных функций.
Контрольная работа № 6 по теме «Решение неравенств»
11. Равносильность уравнений и неравенств системам (7 ч)
Равносильные преобразования уравнений и неравенств. Решение уравнений с помощью систем. Распадающиеся уравнения. Решение неравенств с помощью систем.
-
Системы уравнений с несколькими неизвестными (6 ч)
Равносильность систем. Система-следствие. Основные приемы решения систем уравнений: подстановки, сложения, введения новых переменных. Метод замены неизвестных.
-
Уравнения и неравенства с параметрами (4 ч)
Уравнения с параметром. Неравенства с параметром.
Итоговая контрольная работа № 7
-
Повторение (13 ч)
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений. Решение уравнений и неравенств. Использование свойств и графиков функций при решении уравнений и неравенств. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем. Решение рациональных, иррациональных, показательных, логарифмических уравнений и неравенств.
Требования к уровню подготовки выпускников
В результате изучения математики на базовом уровне и старшей школе ученик должен знать/ понимать:
-
значение математической науки для решения задач, возникающих в теории и практике; широту и, в то же время, ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
-
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
-
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
-
вероятностный характер различных процессов окружающего мира.
Алгебра
уметь:
-
выполнять арифметические действия, сочетая устные и письменные приемы, применения вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
-
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
-
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, при необходимости используя справочные материалы и простейшие вычислительные устройства.
Функции и графики
уметь:
-
определять значение функции по значению аргумента при различных способах задания функции;
-
строить графики изученных функций;
-
описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
-
решать уравнения, простейшие системы уравнений, используя их графики;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.
Начала математического анализа
уметь:
-
вычислять производные элементарных функций, используя справочные материалы;
-
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов с использованием аппарата математического анализа;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
решения прикладных, в том числе социально-экономических и физических, задач на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
Уравнения и неравенства
уметь:
-
решать рациональные, показательные и логарифмические уравнения и неравенства;
-
составлять уравнения по условию задачи;
-
использовать для приближенного решения уравнений и неравенств графический метод;
-
изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
построения и исследования простейших математических моделей.
Элементы комбинаторики, статистики и теории вероятностей
уметь:
-
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
-
вычислять в простейших случаях вероятность событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера.
Для реализации рабочей программы используется программно-методический комплекс:
-
Никольский С.М., Потапов М.К. Алгебра и начала математического анализа (базовый уровень). 10 кл.- М.: Просвещение, 2013.
-
Никольский С.М., Потапов М.К. Алгебра и начала математического анализа (базовый уровень). 11 кл.- М.: Просвещение, 2013.
-
Потапов М.К., Шевкин А.В. Алгебра и начала математического анализа. Дидактические материалы, базовый и профильный уровни. 10 кл.- М.: Просвещение, 2013.
-
Потапов М.К., Шевкин А.В. Алгебра и начала математического анализа. Дидактические материалы, базовый и профильный уровни. 10 кл.- М.: Просвещение, 2013.
-
Потапов М.К., Шевкин А.В. Алгебра и начала математического анализа. Книга для учителя. 10 кл.- М.: Просвещение, 2013.
Приложение
Контрольные работы по алгебре для 10 класса.
Контрольная работа №1 по теме «Рациональные уравнения и неравенства».
Вариант 1
-
Упростить выражение
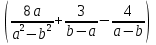 :
: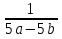 .
.
-
Решит уравнение
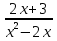 -
- 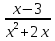 = 0
= 0
-
Решить неравенство a)
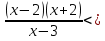 0; б)
0; б) 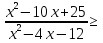 0.
0.
-
Решите систему неравенств
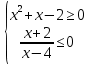 .
.
-
Упростите выражение
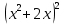 - 2
- 2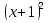 - 1
- 1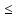 0
0
Вариант 2
-
Упростить выражение
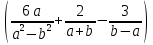 :
: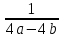 .
.
-
Решит уравнение
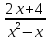 -
- 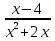 = 0
= 0
-
Решить неравенство a)
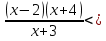 0; б)
0; б) 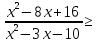 0.
0.
-
Решите систему неравенств
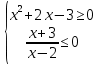 .
.
-
Упростите выражение
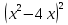 -
- 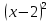 - 16
- 16 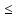 0
0
Контрольная работа №2 по теме «Корень степени n и степень положительного числа».
Вариант 1
-
Найти значение выражения
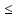 при a =
при a = 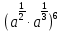 .
. -
Вычислить
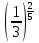
-
Постройте график y=
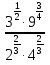 функции и перечислите свойства этой функции.
функции и перечислите свойства этой функции.
-
Упростите выражение (
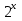 +
+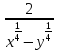 )
)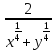 .
.
-
Упростите выражение
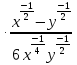 и найдите его значение
и найдите его значение
при x=0,9919.
-
Вычислите предел последовательности:
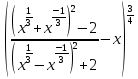 .
.
Вариант 2
-
Найти значение выражения
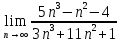 при a =
при a = 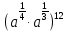 .
. -
Вычислить
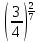
-
Постройте график y=
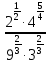 функции и перечислите свойства этой функции.
функции и перечислите свойства этой функции.
-
Упростите выражение (
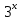 +
+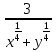 )
)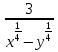 .
.
-
Упростите выражение
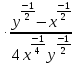 и найдите его значение
и найдите его значение
при x =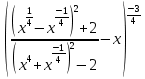 .
.
-
Вычислите предел последовательности:
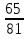 .
.
Контрольная работа №3 по теме «Показательные и логарифмические уравнения и неравенства».
Вариант 1
-
Вычислите :
а) 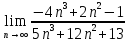 lg100;
lg100;
б) 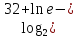 .
.
-
Решите уравнение:
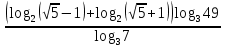 б)
б) 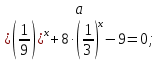 = 9.
= 9.
-
Решите неравенство: а)
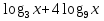 ;
;
б) 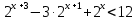
-
Докажите числовое неравенство:
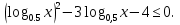
-
Вычислите значение числового выражения:
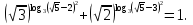 :
: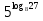 .
.
-
Решите уравнение 2
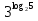 .
.
Вариант 2
-
Вычислите :
а) 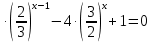 lg1000;
lg1000;
б) 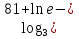 .
.
-
Решите уравнение:
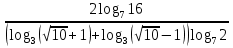 б)
б) 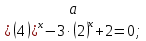 = 8.
= 8.
-
Решите неравенство: а)
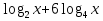 ;
;
б) 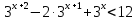
-
Докажите числовое неравенство:
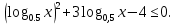
-
Вычислите значение числового выражения:
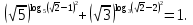 :
: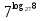 .
.
-
Решите уравнение 5
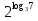 .
.
Контрольная работа №4 по теме «Синус, косинус, тангенс и котангенс угла».
Вариант 1
-
Вычислите: а)
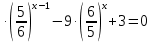 ctg
ctg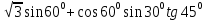 ;
;
б) cos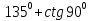 sin
sin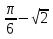 tg
tg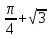 .
.
-
Упростить выражение: а)
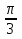 ,
, 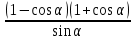 ;
;
б) 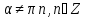 .
.
-
Вычислите: а)
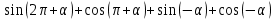 ;
;
б) tg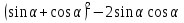 , если
, если 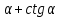 .
.
-
Найдите все такие углы
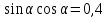 , для каждого из которых выполняется равенство:
, для каждого из которых выполняется равенство:
а) 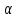 ; б)
; б) 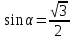 ; в) tg
; в) tg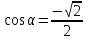 ; г) ctg
; г) ctg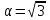 .
.
-
Вычислите: а)
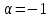 , если tg
, если tg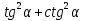 .
.
б) 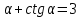 , если tg
, если tg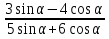 .
.
-
Вычислите arcsin
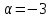 .
.
Вариант 2
-
Вычислите: а)
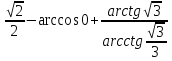 ctg
ctg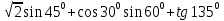 ;
;
б) sin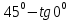 cos
cos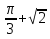 ctg
ctg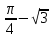 .
.
-
Упростить выражение: а)
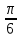 ,
, 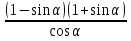 ;
;
б) 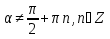 .
.
-
Вычислите: а)
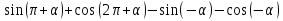 ;
;
б) tg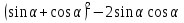 , если
, если 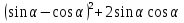 .
.
-
Найдите все такие углы
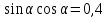 , для каждого из которых выполняется равенство:
, для каждого из которых выполняется равенство:
а) 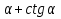 ; б)
; б) 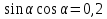 ; в) tg
; в) tg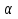 ; г) ctg
; г) ctg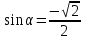 .
.
-
Вычислите: а)
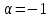 , если tg
, если tg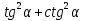 .
.
б) 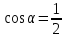 , если tg
, если tg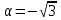 .
.
-
Вычислите arcsin
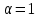 .
.
Контрольная работа №5 по теме «Тригонометрические функции числового аргумента. Формулы сложения».
Вариант 1
-
Упростить выражение:
а) 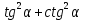 , если
, если 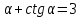 ;
;
б) 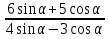 ,
, 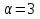 , n
, n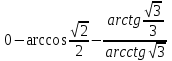
-
Вычислите
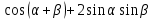 .
. -
Известно, что
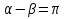 .
.
Вычислите: а) 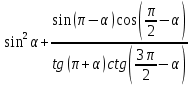 ; б)
; б) 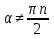 ; в)
; в) 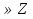 .
.
-
Постройте график функции y
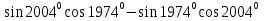 .
. -
Вычислите
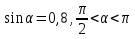 .
. -
Докажите справедливость равенства
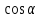 .
.
Вариант 2
-
Упростить выражение:
а) 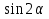 , если
, если 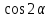 ;
;
б) 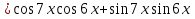 ,
, 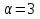 , n
, n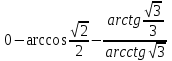
-
Вычислите
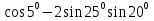 .
. -
Известно, что
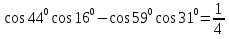 .
.
Вычислите: а) 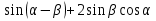 ; б)
; б) 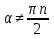 ; в)
; в) 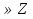 .
.
-
Постройте график функции y
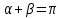 .
. -
Вычислите
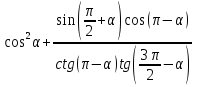 .
. -
Докажите справедливость равенства
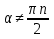 .
.
Контрольная работа №6 по теме «Тригонометрические уравнения и неравенства».
Вариант 1
Решите уравнение (1-5).
-
а)
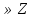 .
. -
а)
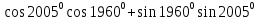 ; б) 3
; б) 3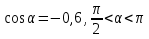 .
. -
а)
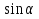 ;
;
б) 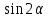 .
.
-
а)
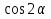 ; б)
; б) 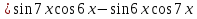 ; в) tgx
; в) tgx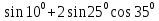 .
. -
а)
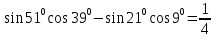 ; б) 2
; б) 2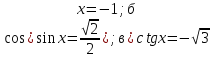 .
. -
Решите неравенство :
а) 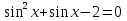 ; б)
; б) 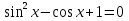 ; в) tgx
; в) tgx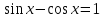 .
.
Вариант 2
Решите уравнение (1-5).
-
а)
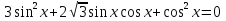 .
. -
а)
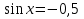 ; б) 3
; б) 3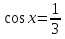 .
. -
а)
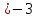 ;
;
б) 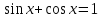 .
.
-
а)
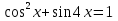 ; б)
; б) 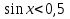 ; в) tgx
; в) tgx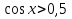 .
. -
а)
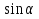 ; б) 2
; б) 2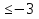 .
. -
Решите неравенство :
а) 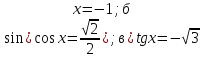 ; б)
; б) 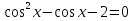 ; в) tgx
; в) tgx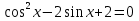 .
.
Итоговая контрольная работа №7
Вариант 1
-
Найти сумму корней уравнения
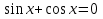 .
. -
Найти наибольшее целое решение неравенства
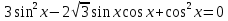 .
. -
Вычислите
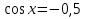 .
. -
Сколько корней уравнения
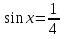 пренадлежит отрезку
пренадлежит отрезку 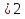 ?
? -
Вычислите
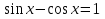 , если
, если 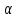 и
и 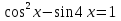 .
. -
Найти значение выражения
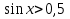 , если
, если 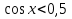 .
.
Вариант 2
-
Найти сумму корней уравнения
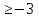 .
. -
Найти наибольшее целое решение неравенства
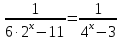 .
. -
Вычислите
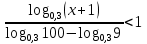 .
. -
Сколько корней уравнения
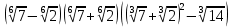 пренадлежит отрезку
пренадлежит отрезку 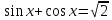 ?
? -
Вычислите
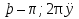 , если
, если 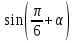 и
и 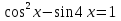 .
. -
Найти значение выражения
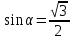 , если
, если 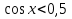 .
.
Критерии оценивания.
Отметка «5» ставится, если:
- в логических и математических рассуждениях и обосновании решения нет пробелов и ошибок;
Отметка «4» ставится, если:
- допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках.
Отметка «3» ставится, если:
-допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
- допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере
22