Урок по алгебре для 7 класса Разложение многочлена на множители с помощью комбинации различных приёмов

Методическая разработка

открытого урока алгебры

«Разложение многочлена на множители с помощью комбинации различных приёмов»

для суворовцев 7-х классов

Разработала:

Казанцева Н.А. преподаватель математики первой категории

Пермь

2016

ПЛАН УРОКА

Класс: 7

Дата: 21.04.2016

Тема: Разложение многочлена на множители с помощью комбинации различных приёмов.

Цель урока: систематизировать, обобщить, и углубить знания, умения применять различные способы разложения многочлена на множители, а также применять разложение многочлена на множители путём комбинации различных приёмов.

Задачи урока:

Обучающие (О) - сформировать умение применять разложение многочлена на множители путём комбинации различных приёмов.

Развивающие (Р) - способствовать развитию наблюдательности, умения анализировать, сравнивать, делать выводы.

Воспитательные (В) - побуждать учеников к само -, взаимоконтролю, работе в команде, вызывать у них потребность в обосновании своих высказываний, формировать умение рефлексировать.

Тип урока: урок применения и совершенствования знаний

Конспект урока

1. Организационный момент.

Приветствие. Проверка подготовки суворовцев к занятию.

2. Постановка цели и мотивация.

Прежде чем начать урок, давайте поиграем в ассоциации. Ребят, какие ассоциации у вас вызывает слово «урок»? Давайте разложим его по буквам,

У - успех, (удача)

Р - радость, (результат)

О - одаренность, (оживлённость)

К - коллектив, (качество).

Надеюсь, что сегодня на уроке нас ждет и успех, и радость. И мы, работая в коллективе, покажем свою знания, умения работать в командах

Будьте внимательны в течение урока. Думайте, спрашивайте, предлагайте.

Математику нельзя изучать, наблюдая как это делает сосед!

3. Актуализация знаний.

• Что мы изучаем с вами уже на протяжении нескольких недель?

(Разложение многочленов на множители)

1) Что называется разложением многочлена на множители?

(Представление многочлена в виде произведения двух или нескольких многочленов)

2) Перечислите методы разложения многочлена на множители.

(1. Вынесение общего множителя за скобки. 2. Формулы сокращенного умножения. 3. Способ группировки.)

• Тема нашего урока сегодня «Разложение многочлена на множители с помощью комбинации различных приемов».

• Сегодня на уроке мы с вами систематизируем, углубим знания и продолжим формировать умение разложения многочлена на множители.

• В тетрадях записываем число, «Классная работа», тему урока.

• А для этого мы вспомним способы разложения на множители и потренируемся раскладывать многочлен на множители с помощью различных способов.

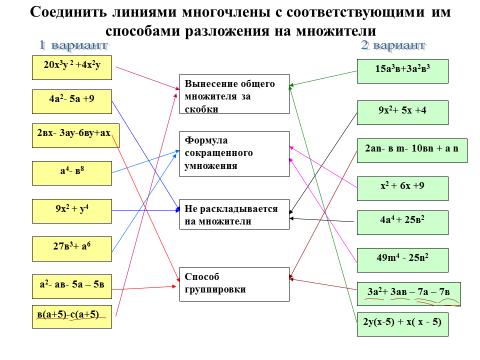
3) Соедините линиями многочлены с соответствующими им способами разложения на множители.

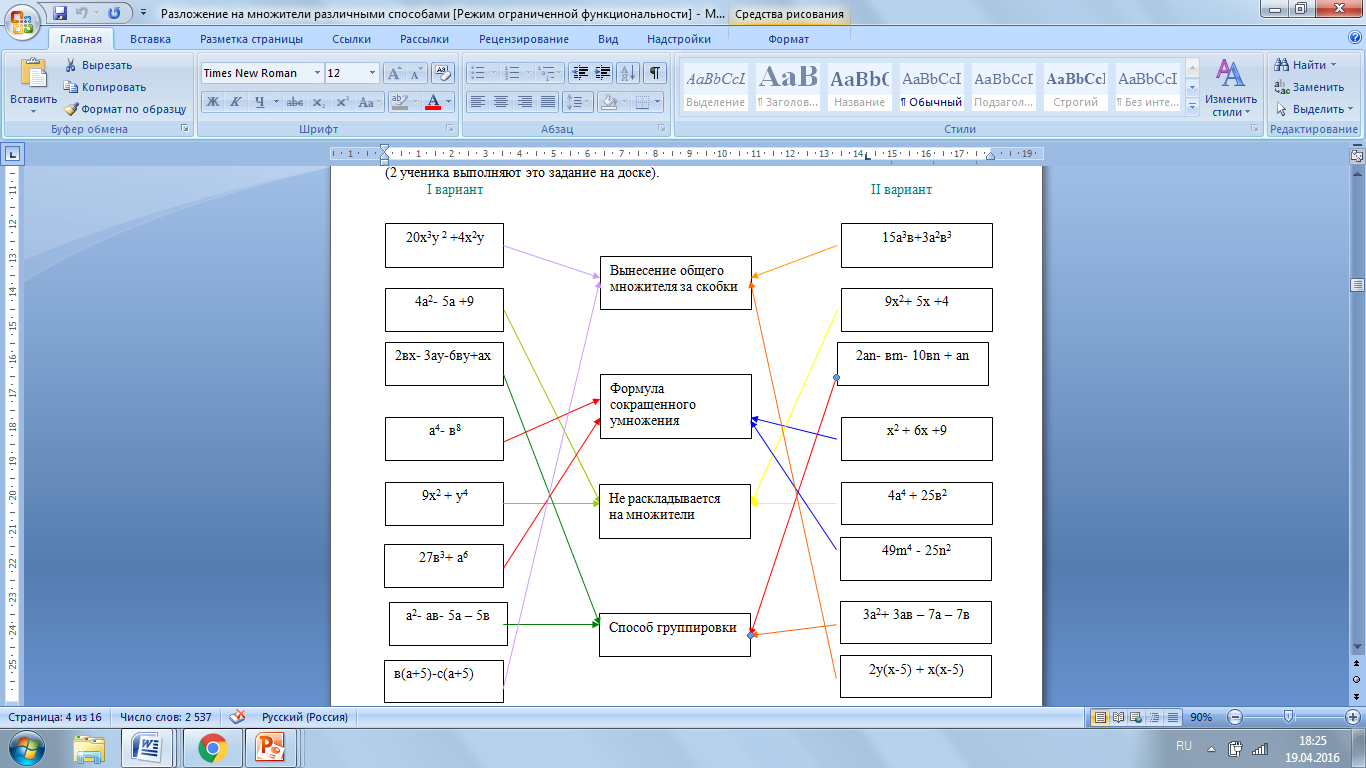
- После выполнения теста сделаем характеристику каждому перечисленному приему.

► Вынесение общего множителя.

Из каждого слагаемого, входящего в многочлен, выносится некоторый одночлен, входящий в качестве множителя во все слагаемые. Таким общим множителем может быть не только одночлен, но и многочлен.

►Применение формул сокращенного умножения.

Группа из двух, трех слагаемых, которая образует выражение, входящее в одну из формул сокращения умножения, заменяется произведением многочленов.

►Группировка.

Бывает, что члены многочлена не имеют общего множителя и нельзя применить формулы сокращенного умножения, но после заключения нескольких членов в скобки (на основе переместительного и сочетательного законов сложения) удается выделить общий множитель, являющийся многочленом, или разложить с помощью формул.

4. Формирование знаний учащихся

- Часто при решении примеров приходится использовать комбинацию различных приемов. Давайте подумаем и постараемся выработать план их последовательного применения.

Разложить многочлен на множители, и указать какие приемы исследовались при этом.

Каждый пример у доски выполняют по одному учащемуся от команды (ряда). В случае затруднения члены команды могут помочь решающему у доски. Остальные учащиеся решают примеры в тетради и проверяют правильность решения.

1) 18а⁶в³ - 48а⁴в⁴ + 32а²в⁵ =

2) а² + 2ав + в² - с² =

3) -3x² + 12x - 12 =

4) n² + n³ + 2n² + 2n =

5. Первичное закрепление

Прошу вас решить тест, но и здесь не просто указать варианты ответов. Каждый вариант ответа подписан координатой точки. Выполнив задания, последовательно отметьте и соедините, получившиеся координаты точек на прямоугольной системе координат. В результате, вы сами поймете - верно ли вы решили. Желаю удачи! (Задание выполняется каждым суворовцев в тетради, затем по очереди обучающиеся выходят к доске и в программе Smart Notebook на координатной плоскости отмечают точки. В результате получается «5»)

1. Вынесите общий множитель за скобки 3 x y +6ay

(0; 1) 3y(x+6a); (3; 4) 3y(x+2a);

(2; 2) 3y(x+6ay); (3; 2) 3y (xy+2a).

2. Вынесите общий множитель за скобки y³-y⁴

(3; 4) y³(y+y²); (3; 6) y³ (1+y³);

(2;5) y³(1-y⁴); (3; 5) y³(1-y).

3. Разложите на множители многочлен -x⁵-3x⁷-2x⁴

(1;4) -x⁴(-x-3x³-2); (0;5) x⁴(-x⁵-3x⁷-2);

(1;5) -x⁴(x+3x³+2); (2;5) -x⁴(x⁵+3x³+2).

4. Вынесите общий множитель за скобки 6a³+9a²-18a

(- 2; 5) 3a (2a²+3a-6); (-1; 5) 3a(2a³+3a²-6a);

(-2; 4) 3a² (2a²+3a-6); (-5; 2) 3a(6a²+9a-18).

5. Разложите на множители многочлен 4x y²-6y³+8y²

(2; 2) 2y² (2x+3y+4); (1; 1) 2y² (2xy-3x+4);

(- 2; 2) 2y ²(2x-3y+4); (2;-2) 2y²(2x-3y).

6. Вынесите общий множитель за скобки 7a²b³-14b²+35b³

(-3; 0) 7b² (a²-2+35b); (0; -2) 7b ²(7ab-2+5b);

(- 2; 0) 7b² (a²b-2+5b); (-2; 2) 7b ²(a²b+2+5b).

7. Представьте в виде произведения a²-a b-7a+7b

(0; 2) (a -b) (a+7); (1; 0) (a-b) (7-a);

(0; 3) (a +b)(a-7); (0; 1) (a-b) (a-7).

8. Представьте в виде произведения x³-x²+x-1

(2;2) (x-1)(1-x²); (2;1) (x-1)(x²+1);

(1;2) x²(x-1); (2;3) (x²+x)(x-1).

9. Разложите на множители многочлен a b-ac-a²+b c

(1;0) (a-c)(b-a); (2;0) (c-a)(b-a);

(3;0) (a +c)(b-a); (0;3) (a +c)(a-b).

10. Представьте в виде произведения 13ax-5a b-26x+10b

(3; - 2) (a -2) (13 x-5b); (3; -4) (3a-6) (4x-b);

(3;-3) (a +2)(3x-5b); (-3; 3) (a-2) (5b-3x).

11. Разложите на множители многочлен 81-4t²

(3; -3) (9-4t²)(9+4t²); (3; - 4) (9-2t)(9+2t);

(-4;3) (9+4t)(9-4t); (3;-5) (9-2t)(9-2t).

12. Представьте в виде квадрата двучлена 16m²-8m n+n²

(2;- 5) (4m-n)²; (-5;2) (4m²-n²)²;

(3;-5) (4m+n)²; (1;-5) (16m-n)².

13. Представьте в виде квадрата двучлена 49x²+42x y²+9y⁴

(1;5) (7x+3y)²; (-1; -5) (7x+3y²)²;

(-1;5) (49x+9y²)²; (1;-5) (7x²+3y⁴)².

14. Представьте в виде произведения y³+1000

(2;4) (y+10)(y²-20y+100); (2;-4) (y-10)(y²+10y+100);

(-2;4) (y+10)(y²+10y+100); (-2; -4) (y+10)(y²-10y+100).

15. Представьте в виде произведения 125-x⁶

(2;3) (5-x²)(25-5x²+x⁴); (2;-3) (5-x²)(25-10x²+x⁴);

(-2; -3) (5-x²)(25+5x²+x⁴); (-2;3) (5+x²)(25-5x²+x⁴).

Резервное задание: вычислите .

6. Подведение итогов занятия

Чему вы сегодня научились на уроке?

Где вы сможете применить эти знания?

Что понравилось?

Какие встретились трудности?

Была ли достигнута цель нашего урока?

Какое у вас настроение после этого урока?

Поднимите руку:

• Если ваше отношение к уроку «Я ничего не понял, и у меня совсем ничего не получилось»

• Если ваше отношение к уроку «были сложности, но я справился»

• Если ваше отношение к уроку «У меня получилось почти все»

Конечно - же домашнее задание.

- Вам предлагается выполнить самостоятельную работу на закрепление темы.

Разложить на множители, используя различные способы.

1 вариант 2 вариант

1. 5а³ - 125ав² 1. 63ав³ - 7а²в

2. а² - 2ав +в² - ас +вс 2. n² +6mn +9n² - m - 3n

3. в² - а² - 12а - 36 3. а² +в² - 2ав - 25

4. p² - 16c² - p - 4с 4. 4а² - в² - 2а + в

5. а² + 6а + 6в - в² 5. х² - 7х +7у - у²

Приложение 1

Дидактические материалы

Решите тест. Каждый вариант ответа подписан координатой точки. Выполнив задания, последовательно отметьте и соедините, получившиеся координаты точек на прямоугольной системе координат. В результате, вы сами поймете- верно ли вы решили. Желаю удачи!

1. Вынесите общий множитель за скобки 3 x y +6ay

(0; 1) 3y(x+6a); (3; 4) 3y(x+2a);

(2; 2) 3y(x+6ay); (3; 2) 3y (xy+2a).

2. Вынесите общий множитель за скобки y³-y⁴

(3; 4) y³(y+y²); (3; 6) y³ (1+y³);

(2;5) y³(1-y⁴); (3; 5) y³(1-y).

3. Разложите на множители многочлен -x⁵-3x⁷-2x⁴

(1;4) -x⁴(-x-3x³-2); (0;5) x⁴(-x⁵-3x⁷-2);

(1;5) -x⁴(x+3x³+2); (2;5) -x⁴(x⁵+3x³+2).

4. Вынесите общий множитель за скобки 6a³+9a²-18a

(- 2; 5) 3a (2a²+3a-6); (-1; 5) 3a(2a³+3a²-6a);

(-2; 4) 3a² (2a²+3a-6); (-5; 2) 3a(6a²+9a-18).

5. Разложите на множители многочлен 4x y²-6y³+8y²

(2; 2) 2y² (2x+3y+4); (1; 1) 2y² (2xy-3x+4);

(- 2; 2) 2y ²(2x-3y+4); (2;-2) 2y²(2x-3y).

6. Вынесите общий множитель за скобки 7a²b³-14b²+35b³

(-3; 0) 7b² (a²-2+35b); (0; -2) 7b ²(7ab-2+5b);

(- 2; 0) 7b² (a²b-2+5b); (-2; 2) 7b ²(a²b+2+5b).

7. Представьте в виде произведения a²-ab-7a+7b

(0; 2) (a -b) (a+7); (1; 0) (a-b) (7-a);

(0; 3) (a +b)(a-7); (0; 1) (a-b) (a-7).

8. Представьте в виде произведения x³-x²+x-1

(2;2) (x-1)(1-x²); (2;1) (x-1)(x²+1);

(1;2) x²(x-1); (2;3) (x²+x)(x-1).

9. Разложите на множители многочлен a b-ac-a²+bc

(1;0) (a-c)(b-a); (2;0) (c-a)(b-a);

(3;0) (a +c)(b-a); (0;3) (a +c)(a-b).

10. Представьте в виде произведения 13ax-5a b-26x+10b

(3; - 2) (a -2) (13 x-5b); (3; -4) (3a-6) (4x-b);

(3;-3) (a +2)(3x-5b); (-3; 3) (a-2) (5b-3x).

11. Разложите на множители многочлен 81-4t²

(3; -3) (9-4t²)(9+4t²); (3; - 4) (9-2t)(9+2t);

(-4;3) (9+4t)(9-4t); (3;-5) (9-2t)(9-2t).

12. Представьте в виде квадрата двучлена 16m²-8mn+n²

(2;- 5) (4m-n)²; (-5;2) (4m²-n²)²;

(3;-5) (4m+n)²; (1;-5) (16m-n)².

13. Представьте в виде квадрата двучлена 49x²+42xy²+9y⁴

(1;5) (7x+3y)²; (-1; -5) (7x+3y²)²;

(-1;5) (49x+9y²)²; (1;-5) (7x²+3y⁴)².

14. Представьте в виде произведения y³+1000

(2;4) (y+10)(y²-20y+100); (2;-4) (y-10)(y²+10y+100);

(-2;4) (y+10)(y²+10y+100); (-2; -4) (y+10)(y²-10y+100).

15. Представьте в виде произведения 125-x⁶

(2;3) (5-x²)(25-5x²+x⁴); (2;-3) (5-x²)(25-10x²+x⁴);

(-2; -3) (5-x²)(25+5x²+x⁴); (-2;3) (5+x²)(25-5x²+x⁴).

1 вариант

2 вариант

Разложите на множители, используя различные способы.

1. 5а³ - 125ав²

2. а² - 2ав +в² - ас +вс

3. в² - а² - 12а - 36

4. p² - 16c² - p - 4с

5. а² + 6а + 6в - в²

Разложите на множители, используя различные способы.

1. 63ав³ - 7а²в

2. n² +6mn +9n² - m - 3n

3. а² +в² - 2ав - 25

4. 4а² - в² - 2а + в

5. х² - 7х +7у - у²

Соединить линиями многочлены с соответствующими им

способами разложения на множители.

2 вариант

Соединить линиями многочлены с соответствующими

им способами разложения на множители.

1 вариант

Приложение 2

Презентация к уроку

Слайд 8

Слайд 9