- Учителю
- Методическая разработка игры по геометрии (8 класс)
Методическая разработка игры по геометрии (8 класс)
Владимирская область
Петушинский район
Муниципальное бюджетное общеобразовательное учреждение
«Глубоковская основная общеобразовательная школа»
Методическая разработка
игры по геометрии
для учащихся 8 класса
Учитель-составитель: Валентонене Татьяна Николаевна,
учитель математики
2015
Игра по геометрии для 8 класса
«Математический бой», посвященный теореме Пифагора
(проводится сразу после изучения теоремы Пифагора)
Цели:
1. Активизация деятельности учащихся.
2. Развитие умений формулировать и излагать мысль, моделировать ситуацию.
3. Развитие творческого интереса к математике.
4. Развитие кругозора учащихся.
5. Воспитание стойкости, находчивости, любознательности.
Оборудование: раздаточный материал, доска, мел, призы, грамоты, таблица результатов.
Программа проведения игры:
1. Вступление.
2. Приветствие команд (название, девиз, эмблема).
3. Конкурсные задания.
4. Подведение итогов.
1. Вступление (звучит музыка)
Мы рады приветствовать всех собравшихся. Приветствуем всех, кто любит математику, кто учит математику, кто занимается и увлекается математикой! Мы обещаем приятное проведение времени.
2. Приветствие команд
Команды представляют свое домашнее задание - название команды, девиз, приветствие, эмблема.
Жюри оценивает конкурс по четырех бальной системе.
3. Конкурсная часть
Конкурс 1 «Разминка»: за две минуты команды отвечают на свои вопросы, верный ответ приносит команде балл.
Вопросы 1 команде:
1. Чему равна сумма углов в треугольнике? (180).
2. Прямая, имеющая только одну общую точку с окружностью. (Касательная).
3. Математическое предложение, не требующее доказательства. (Аксиома).
4. Как называется направленный отрезок. (Вектор).
5. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны. (Медиана).
6. Сколько различных биссектрис можно провести в треугольнике? (три).
7. Отрезок, соединяющий две точки окружности. (Хорда).
8. Инструмент для измерения углов на плоскости. (Транспортир).
9. Площадь квадрата равна 49 см . Чему равен периметр этого квадрата? (28).
10. На какой угол поворачивается солдат по команде "кругом"? (180).
Вопросы 2 команде:
1. Луч, делящий угол пополам. (Биссектриса).
2. Четырёхугольник, у которого только две стороны параллельны. (Трапеция).
3. Предложение, истинность которого нужно доказать. (Теорема).
4. Кратчайшее расстояние от точки до прямой. (Перпендикуляр).
5. Отрезок, соединяющий середины сторон. (Средняя линия).
6. Вычислите площадь квадрата, если его периметр 40 см. (100 см ).
7. Параллелограмм, у которого все стороны равны. (Ромб).
8. Наибольшая хорда в окружности. (Диаметр).
9. Число π равно ... (3,14).
10. Сколько осей симметрии у равностороннего треугольника. (Три)
Конкурс 2 «Совет мудрецов»: каждая команда должна записать формулировку теоремы Пифагора и доказательство этой теоремы на доске, в течении пяти-семи минут. Далее, каждая команда выступает с доказательством теоремы перед соперниками и жюри. Оценивается точность формулировки, грамотность записи, точность и последовательность доказательства, чертеж, оригинальность доказательства, стиль изложения. Максимально возможный балл за данный конкурс-20-ть баллов.( Либо дается все в качестве домашнего задания)
Конкурс 3 «Вычислялочки». Каждая команда должна применить теорему Пифагора при выполнении следующего задания. Требуется заполнить таблицу, содержащую только измерения двух катетов. Каждое верно выполненное задание приносит команде 2 балл, дополнительные три балла получает сдавшая раньше других команда, если все вычисления верны.
№
a
b
a2
b2
a2+b2=c2
c
1
3
4
2
5
12
3
8
15
4
7
24
5
20
21
6
12
35
7
9
40
Конкурс 4: «Формулы»
Командам нужно из формулы a2+b2=c2 выразить все величины. Каждый верный ответ приносит команде 1 балл.
Конкурс 5: «Египетские треугольники»
Каждая команда должна применить теорему Пифагора и итоги конкурса «Формулы» при выполнении следующего задания. Требуется заполнить таблицу, содержащую только измерения двух сторон прямоугольного треугольника. Каждое верно выполненное задание приносит команде 2 балл, дополнительные три балла получает сдавшая раньше других команда, если все вычисления верны.
a
b
c
21
72
10
24
60
100
Конкурс 6: «Знания в дело»
Командам нужно решить задачу. Верное решение приносит команде 15 баллов.
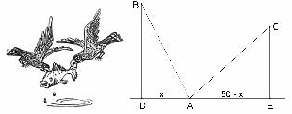
На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой -20 локтей. Расстояние между их основаниями - 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?
4. Подведение итогов
В ходе игры формировалась таблица результатов, жюри суммирует баллы и называет команду-победителя. Команды победителей и призеров награждаются грамотами и символическими призами.