- Учителю
- Разработка лекционного занятия для СПО по математике по теме Матрицы для 2 курса
Разработка лекционного занятия для СПО по математике по теме Матрицы для 2 курса
ФИНАНСЫ Лекция 1
Раздел 1. Основы линейной алгебры
Тема 1.1. Матрицы и операции над матрицами. Определители и их свойства
Цель: приобретение базовых знаний в области фундаментального раздела математики - линейной алгебры. Изучить понятие матрицы, её видов, операции над матрицами, определителей и их свойств.
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
</ Вид занятия: Комбинированное занятие, включающее в себя ознакомление с новым материалом, применение знаний и умений на практике, закрепление изученного.
Ход занятия.
1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;
2.Проверка готовности студентов к занятию;
3.Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
-
Изучить теоретический материал по теме «Матрицы. Выполнение операций над матрицами. Определители и их свойства».
-
Рассмотреть примеры решения типовых заданий.
-
Ответить на контрольные вопросы.
-
Организационный момент.
Приветствует обучающихся. Проверяет подготовленность к учебному занятию, организует внимание обучающихся. Обеспечивает благоприятный настрой.
Создание проблемной ситуации при постановке темы, цели и задач лекции.
В школьном курсе алгебры 7 - 9 классов рассматриваются различные способы решения систем линейных уравнений: метод подстановки, метод сложения, метод двойного сложения, графический метод, метод сравнения. Возникает вопрос, а существуют ли какие-либо другие способы решения данных систем. Действительно, кроме методов, изучаемых в школе, существуют и другие, доступные для учащихся старших классов методы решения систем линейных уравнений: метод Крамера, метод Гаусса, матричный метод. Эти методы способствуют развитию внимания, памяти. При применении этих методов встречаются новые понятия: «матрица», «определитель», «минор», «дополнение». Возникает необходимость уметь вычислять определители, миноры, дополнения.
При решении систем линейных уравнений методом Гаусса также нужно уметь выполнять преобразования над строками матриц.
Что же такое матрица, какие действия с ними можно выполнять?
-
Изучение нового материала.
-
Определение матрицы.
Совокупность чисел, расположенных в виде прямоугольной таблицы,
состоящей из ![]() строк и
строк и ![]() столбцов, называют матрицей порядка
столбцов, называют матрицей порядка ![]() (
( ![]() на
на ![]() ) и обозначают символом
) и обозначают символом ![]() . В общем виде матрица выглядит так
. В общем виде матрица выглядит так
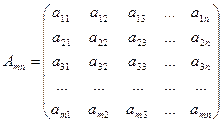 .
.
Числа ![]() называют элементами матрицы. Каждый элемент имеет два индекса:
первый показывает номер строки, в которой стоит этот элемент, а
второй - номер столбца. Размерность матрицы указывать не
обязательно. При
называют элементами матрицы. Каждый элемент имеет два индекса:
первый показывает номер строки, в которой стоит этот элемент, а
второй - номер столбца. Размерность матрицы указывать не
обязательно. При ![]() матрицу называют матрицей-строкой, а при
матрицу называют матрицей-строкой, а при ![]() - матрицей-столбцом.
- матрицей-столбцом.
Матрицу, все элементы которой, равны нулю, называют нулевой
матрицей и обычно обозначают ![]() .
.
Таким образом, 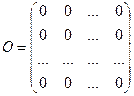 .
.
Если число строк матрицы совпадает с числом ее столбцов, т.е.
![]() , то матрицу называют квадратной
, то матрицу называют квадратной ![]() порядка и обозначают символом
порядка и обозначают символом ![]() . В квадратной матрице
. В квадратной матрице ![]() элементы с одинаковыми индексами
элементы с одинаковыми индексами ![]() называют элементами главной диагонали, а элементы, сумма индексов
которых равна
называют элементами главной диагонали, а элементы, сумма индексов
которых равна ![]()
![]() , элементами побочной диагонали. Во множестве квадратных матриц
особую роль играет матрица
, элементами побочной диагонали. Во множестве квадратных матриц
особую роль играет матрица
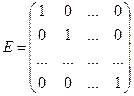 .
.
Ее называют единичной матрицей. Все элементы ее главной диагонали равны единице, а все остальные элементы - нули.
Квадратную матрицу называют треугольной, если все ее элементы,
стоящие ниже или выше элементов главной диагонали, равны нулю.
Например, матрицы  и
и 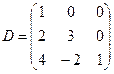 треугольные, причем матрицу
треугольные, причем матрицу ![]() называют верхнетреугольной, а матрицу
называют верхнетреугольной, а матрицу ![]() - нижнетреугольной.
- нижнетреугольной.
Определение. Две матрицы одинакового порядка ![]() и
и ![]() называют
называют
равными и пишут ![]() =
= ![]() , если все элементы с одинаковыми
, если все элементы с одинаковыми
индексами обеих матриц совпадают.
Матрицей размером тп называется прямоугольная таблица, составленная из тп чисел и имеющая т строк и п столбцов. Числа ij, составляющие матрицу, называются элементами матрицы. Каждый элемент матрицы снабжен двумя индексами: первый индекс указывает номер строки, второй - номер столбца, в котором расположен этот элемент.
Для изображения матрицы употребляют круглые скобки и часто обозначают ее одной буквой, например,
А=(ij)=  (1)
(1)
Первый индекс i (i = 1, 2, …m) обозначает номер строки, второй j (j = 1, 2, …n) - столбец матрицы. Матрицу принято обозначать заглавными буквами, например А, В, С и т.д.
Горизонтальный ряд чисел называется строкой, а вертикальный - столбцом.
Определение. Если т = п, то матрица называется квадратной матрицей порядка n. Число ее строк или столбцов называется порядком матрицы.
Определение. Если же m n, то матрица называется прямоугольной матрицей.
Определение. Две матрицы считаются равными, если они имеют одинаковые размеры и их соответствующие элементы равны. Пусть А = (ij) размером т п, В = (ij) размером pq. A = B, если m = p, n = q и ij = ij для i = 1, 2, …, m, j = 1, 2, …, n.
Определение. Последовательность элементов квадратной матрицы с одинаковыми индексами (i = j) называется главной диагональю матрицы (11, 22, 33,…,nn)/
Определение. Если в квадратной матрице все недиагональные элементы равны нулю (ij= 0, при i = j), то матрица называется диагональной.
А = 
Определение. Квадратная диагональная матрица, у которой элементы главной диагонали равны единице, называется единичной матрицей Е.
А = 
Определение. Матрица, все элементы которой равны нулю, называется нуль-матрицей.
Определение. Матрица, состоящая только из одной строки, называется матрицей-строкой.
Определение. Матрица, состоящая только из одного столбца, называется матрицей-столбцом.
Определение. Матрицу Аt называют транспонированной по отношению к матрице А ,если она получена из матрицы А заменой строк этой матрицы её столбцами, и, наоборот, столбцов строками.
Например, пусть А - матрица размеров т п:

транспонированная ей матрица:

Можно сказать, что транспонированная матрица получается переворачиванием матрицы вокруг главной диагонали.
Переход от матрицы А к матрице Аt называют операцией транспонирования.
Перечислим свойства операции транспонирования:
-
(At)t = A,
-
(A + B)t = At + Bt,
-
(A)t = At,
-
(AB)t = BtAt.
2. Операции над матрицами.
Определение. Суммой двух матриц А = (ij) и В = (ij) одинаковых размеров т п называется матрица С того же размера, элементы которых равны сумме соответствующих элементов матриц А и В. С=А + В = (ij + ij) для i = 1, 2, …, m, j = 1, 2, …, n. Ясно, что сложение матриц сводится к сложению всех пар соответствующих элементов. Для матриц разных размеров сумма не определена.
Сложение матриц подчиняется законам:
-
А + В = В + А (переместительный закон)
-
(А + В) + С = А + (В + С) (сочетательный закон)
-
А + О = О + А = А.
Для любой матрицы А размеров т п существует матрица В тех же размеров такая, что А + В = В + А = О. При этом если А = (ij) и В = (ij), то ij = - ij. Матрица В называется матрицей, противоположной матрице А и обозначается - А.
Определение. Произведением матрицы А = (ij) размером т п на число называется матрица (ij) тех же размеров, которая обозначается А.
Свойства умножения матрицы на число:
1. (А) = ()А.
-
( + )А = А + А.
-
(А + В) = А + В.
-
1А = А.
Разность двух матриц А и В одинаковых размеров определяется равенствами:
А - В = А + (- В) = А + (-1)В.
Определение. Произведением матрицы А = (ij) размеров т п на матрицу В = (ij) размеров nk называется матрица С = (сij) размеров mk, каждый элемент сij которой вычисляется по формуле
сij = i11j + i22j + … + innj , i = 1,2,…,m; j = 1,2,…,n. (2)
Другими словами, элемент сij равняется сумме произведений элементов строки с номером i матрицы А на соответствующие элементы столбца с номером j матрицы В. Произведение матрицы А на матрицу В обозначается АВ.
Замечание: Операция умножения двух матриц выполнима лишь в том случае, когда число столбцов первой матрицы - сомножителя А должно равняться числу строк второй матрицы сомножителя В. Если это условие не выполнено, произведение не существует.
Для запоминания формулы (2) пользуются мнемоническим правилом: «умножение i-той строки матрицы А на j-тый столбец матрицы В».
Приведем примеры умножения матриц.
-
Вычислить произведение АВ, где
![]()
Число столбцов в первой матрице совпадает с числом строк во второй матрице, поэтому произведение АВ существует. Положим С = АВ. В матрице С столько же строк, сколько в матрице А, и столько же столбцов, сколько в матрице В, т.е. матрица С размеров 23. Пусть С = (сij), тогда по формуле (2) получаем
с11 = 2(-1) + 32 = 4, с12 = 22 + 31 = 7, с13 = 20 + 3(-1) = - 3,
с21 =(-1)(-1) + 42 = 9, с22 =(-1)2 + 41 = 2, с23 = (-1)0 + 4(-1) =-4.
Записав эти числа в матрицу, получим
![]()
Заметим, что произведение ВА не существует, поскольку число столбцов в матрице В не равно числу строк в матрице А.
2. 
3. 
4. 
5. 
Свойства умножения матриц:
Умножение матриц в некоторых отношениях похоже на умножение чисел, а в других отношениях отличается от умножения чисел.
-
Для чисел = . Для матриц из существования произведения АВ даже не следует существование произведения ВА (см. пример 1 из предыдущего пункта). Если оба произведения АВ и ВА существуют, то это могут быть матрицы разных размеров (см. примеры 4 и 5 из предыдущего пункта). Даже если матрицы АВ и ВА существуют и имеют одинаковые размеры, в общем случае АВ ВА. Например,
![]()
![]()
-
Если для чисел = 0, то один из сомножителей равен нулю. Но для матриц, как видно из приведенного примера, равенство АВ = О может выполняться и в случае, когда А О и В О.
-
Умножение матриц, подобно умножению чисел, подчиняется ассоциативному закону:
(АВ)С = А(ВС).
-
Известно, что сложение и умножение чисел связаны дистрибутивным законом. Свойство дистрибутивности умножения относительно сложения для матриц выражается двумя равенствами:
(А + В)С = АС + ВС,
А(В + С) = АВ + АС.
-
(АВ) = (А)В = А(В).
Рассмотрим теперь операцию умножения матрицы на матрицу. Пусть имеем матрицу
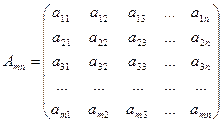
и матрицу
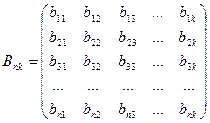 .
.
Сразу же обратим внимание на размерность матриц: число столбцов
матрицы ![]() равно числу строк матрицы
равно числу строк матрицы ![]() . Это условие является необходимым для того, чтобы можно было
матрицу
. Это условие является необходимым для того, чтобы можно было
матрицу ![]() умножить на матрицу
умножить на матрицу ![]() .
.
Будем рассматривать элементы каждой строки матрицы ![]() как координаты
как координаты ![]() мерных векторов:
мерных векторов:
![]() ;
;
![]() ;
;
![]()
…………………….
![]() .
.
Аналогично элементы каждого столбца матрицы ![]() также будем рассматривать как координаты
также будем рассматривать как координаты ![]() мерных векторов:
мерных векторов:
![]() ;
;
![]() ;
;
![]() ;
;
……………………
![]()
Произведением матрицы ![]() на матрицу
на матрицу ![]() назовем матрицу
назовем матрицу 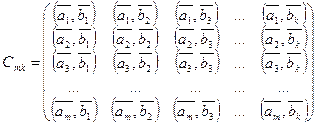 .
.
Как видим, элементами матрицы ![]() являются скалярные произведения векторов
являются скалярные произведения векторов ![]() , где
, где ![]() на векторы
на векторы ![]() , где
, где ![]() .
.
Рассмотрим свойства операции умножения матриц. Из определения
операции умножения матрицы ![]() на матрицу
на матрицу ![]() вовсе не следует, что можно умножить матрицу
вовсе не следует, что можно умножить матрицу ![]() на матрицу
на матрицу ![]() . Это осуществимо только при условии, что
. Это осуществимо только при условии, что ![]() . В противном случае произведение
. В противном случае произведение ![]() просто не существует. Следовательно, бессмысленно говорить о
коммутативности операции умножения матриц. Однако имеют место
свойства ассоциативности:
просто не существует. Следовательно, бессмысленно говорить о
коммутативности операции умножения матриц. Однако имеют место
свойства ассоциативности: ![]() и дистрибутивности:
и дистрибутивности: ![]() ;
; ![]() , которые легко проверяются.
, которые легко проверяются.
Очевидно, что если ![]() и
и ![]() квадратные матрицы одного порядка, то существуют произведения
квадратные матрицы одного порядка, то существуют произведения
![]() и
и ![]() , но нельзя утверждать, что
, но нельзя утверждать, что ![]() . Если же матрицы
. Если же матрицы ![]() и
и ![]() таковы, что
таковы, что ![]() , то их называют перестановочными.
, то их называют перестановочными.
Особую роль при умножении квадратных матриц играет единичная
матрица 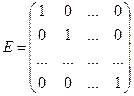 . Легко показать, что для любой квадратной матрицы
. Легко показать, что для любой квадратной матрицы ![]() имеет место равенство
имеет место равенство ![]() , т.е во множестве квадратных матриц
, т.е во множестве квадратных матриц ![]() порядка матрица
порядка матрица ![]() является аналогом числа 1 во множестве действительных чисел.
является аналогом числа 1 во множестве действительных чисел.
Пусть имеем матрицу 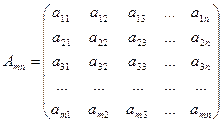 . Если в ней поменять местами строки и столбцы, сохранив их
порядок, то получим матрицу
. Если в ней поменять местами строки и столбцы, сохранив их
порядок, то получим матрицу 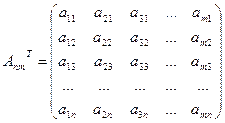 , которую называют транспонированной для
, которую называют транспонированной для ![]() .
.
Легко заметить следующие два свойства операции транспонирования матрицы:
1°. Если матрицу ![]() транспонировать дважды, то в результате получим исходную матрицу
транспонировать дважды, то в результате получим исходную матрицу
![]() :
: ![]() .
.
2°. При транспонировании квадратной матрицы элементы главной диагонали не меняются.
Определение 4. Если квадратная матрица ![]() совпадает со своей
совпадает со своей
транспонированной матрицей ![]() , то ее называют
, то ее называют
симметрической.
Из определения симметрической матрицы видно, что ее элементы
должны быть симметричны относительно главной диагонали. Например,
матрица 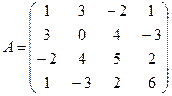 является симметрической, а матрица
является симметрической, а матрица ![]() - нет.
- нет.
-
Определители и их свойства.
Рассмотрим квадратную матрицу второго порядка 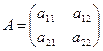 . Определителем этой матрицы называют число, обозначаемое
. Определителем этой матрицы называют число, обозначаемое
![]() , или
, или ![]() , или
, или 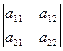 , полученное из элементов матрицы
, полученное из элементов матрицы ![]() по следующему правилу:
по следующему правилу: 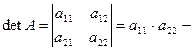
![]() . Например, если
. Например, если ![]() , то
, то ![]()
![]() .
.
Рассмотрим теперь квадратную матрицу третьего порядка 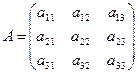 . Определителем этой матрицы назовем число
. Определителем этой матрицы назовем число ![]() .
.
![]() =
= 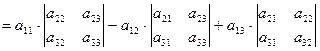 , или
, или
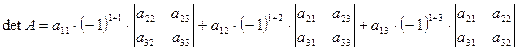 (1)
(1)
Равенство (1) называют разложением определителя по элементам первой строки.
Выражения 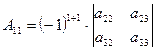 ;
; 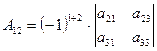 и
и 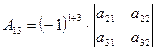 называют алгебраическими дополнениями элементов
называют алгебраическими дополнениями элементов ![]() ,
, ![]() и
и ![]() соответственно. Таким образом, разложение определителя третьего
порядка по элементам первой строки может быть записано в виде:
соответственно. Таким образом, разложение определителя третьего
порядка по элементам первой строки может быть записано в виде:
![]() .
.
Нетрудно заметить, что аналогичным образом определитель третьего порядка может быть разложен по элементам второй и третьей строк, а также по элементам первого, второго или третьего столбца.
Рассмотрим теперь квадратную матрицу ![]() го порядка
го порядка ![]() . Определителем такой матрицы, разложенным по
. Определителем такой матрицы, разложенным по ![]() ой строке, назовем число
ой строке, назовем число
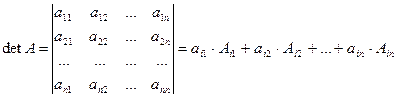 , где
, где ![]() - элементы
- элементы ![]() ой строки, а
ой строки, а ![]() - их алгебраические дополнения.
- их алгебраические дополнения.
Рассмотрим основные свойства определителей.
1). При умножении всех элементов любой строки матрицы ![]() на некоторое число определитель исходной матрицы умножается на это
число.
на некоторое число определитель исходной матрицы умножается на это
число.
2). Определитель матрицы, содержащей нулевую строку, равен нулю.
3). При перестановке местами любых двух строк матрицы ![]() без изменения остальных строк определитель меняет знак.
без изменения остальных строк определитель меняет знак.
4). Определитель матрицы, содержащей две одинаковые строки, равен нулю.
5). Определитель матрицы ![]() не изменится, если к любой строке матрицы прибавить любую другую
строку, умноженную на некоторое число.
не изменится, если к любой строке матрицы прибавить любую другую
строку, умноженную на некоторое число.
6). Определитель произведения двух квадратных матриц одинакового порядка равен произведению определителей этих матриц.
7). При транспонировании квадратной матрицы ее определитель не меняется.
Квадратную матрицу ![]() называют вырожденной
называют вырожденной
(невырожденной), если ![]()
![]() .
.
Число ![]() называют собственным числом матрицы
называют собственным числом матрицы ![]() , если оно является корнем уравнения
, если оно является корнем уравнения ![]() .
.
-
Закрепление нового материала.
Пример 1: Найти сумму матриц: А = 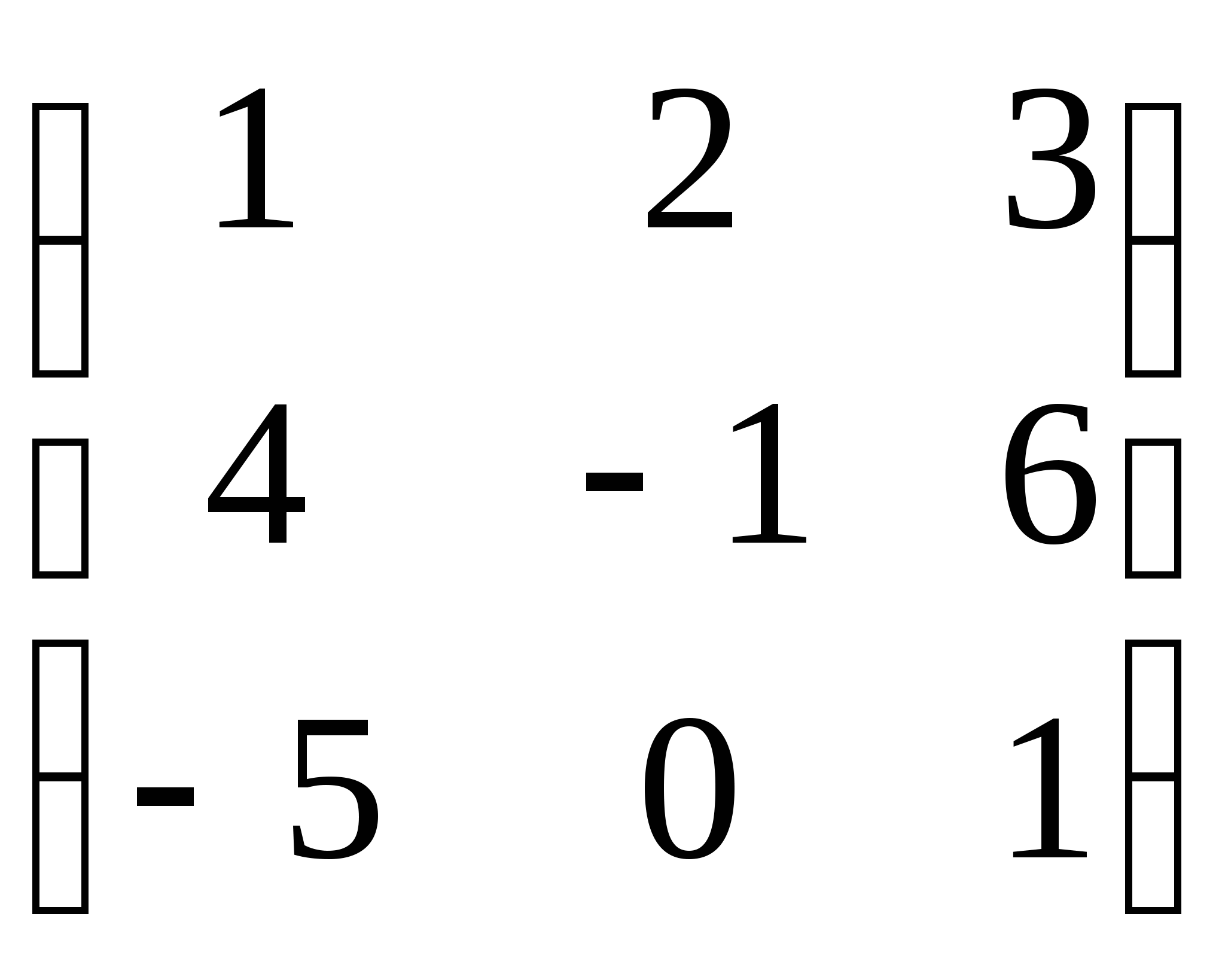 и В =
и В = 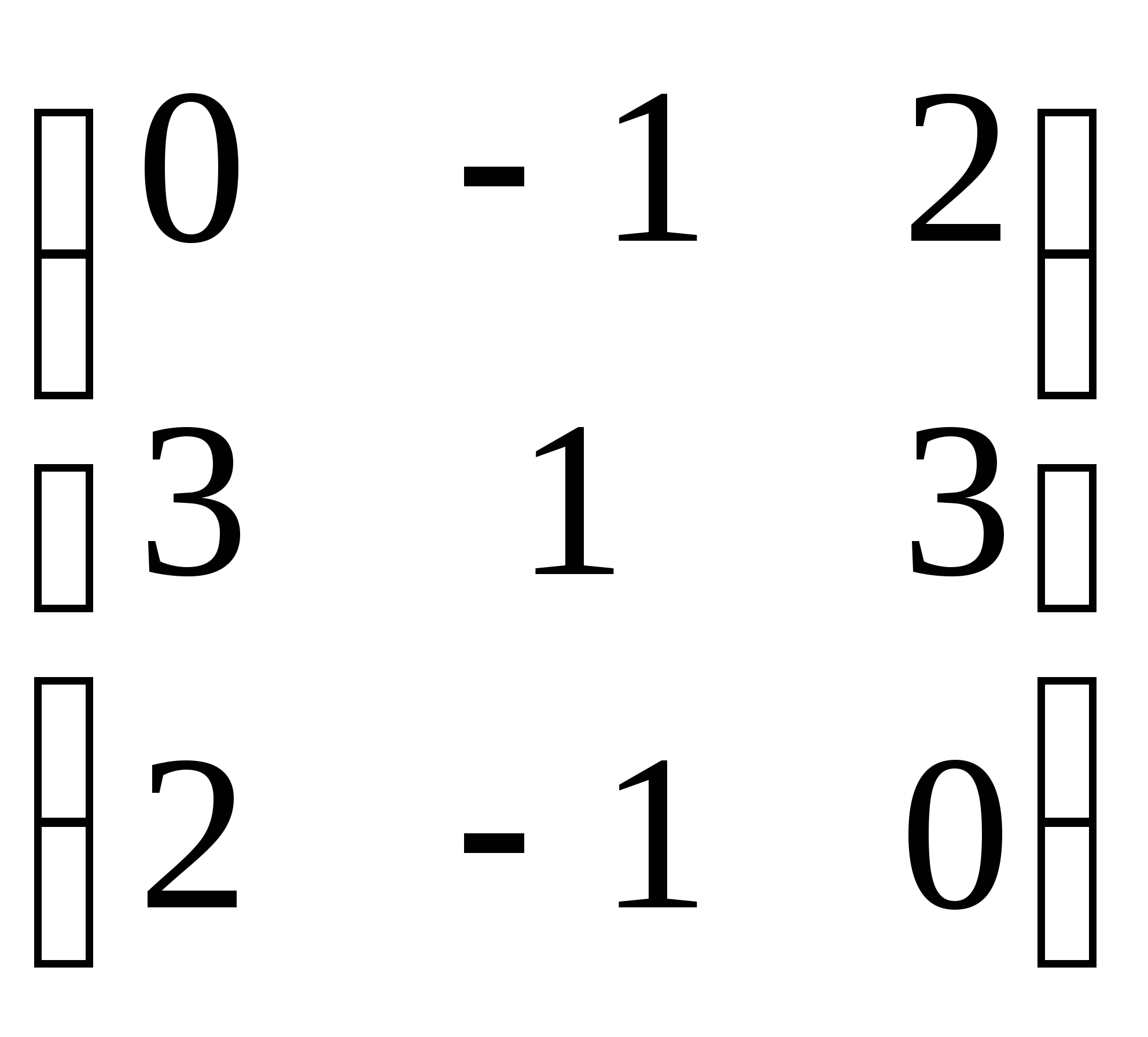 .
.
Решение: С = А + В С = 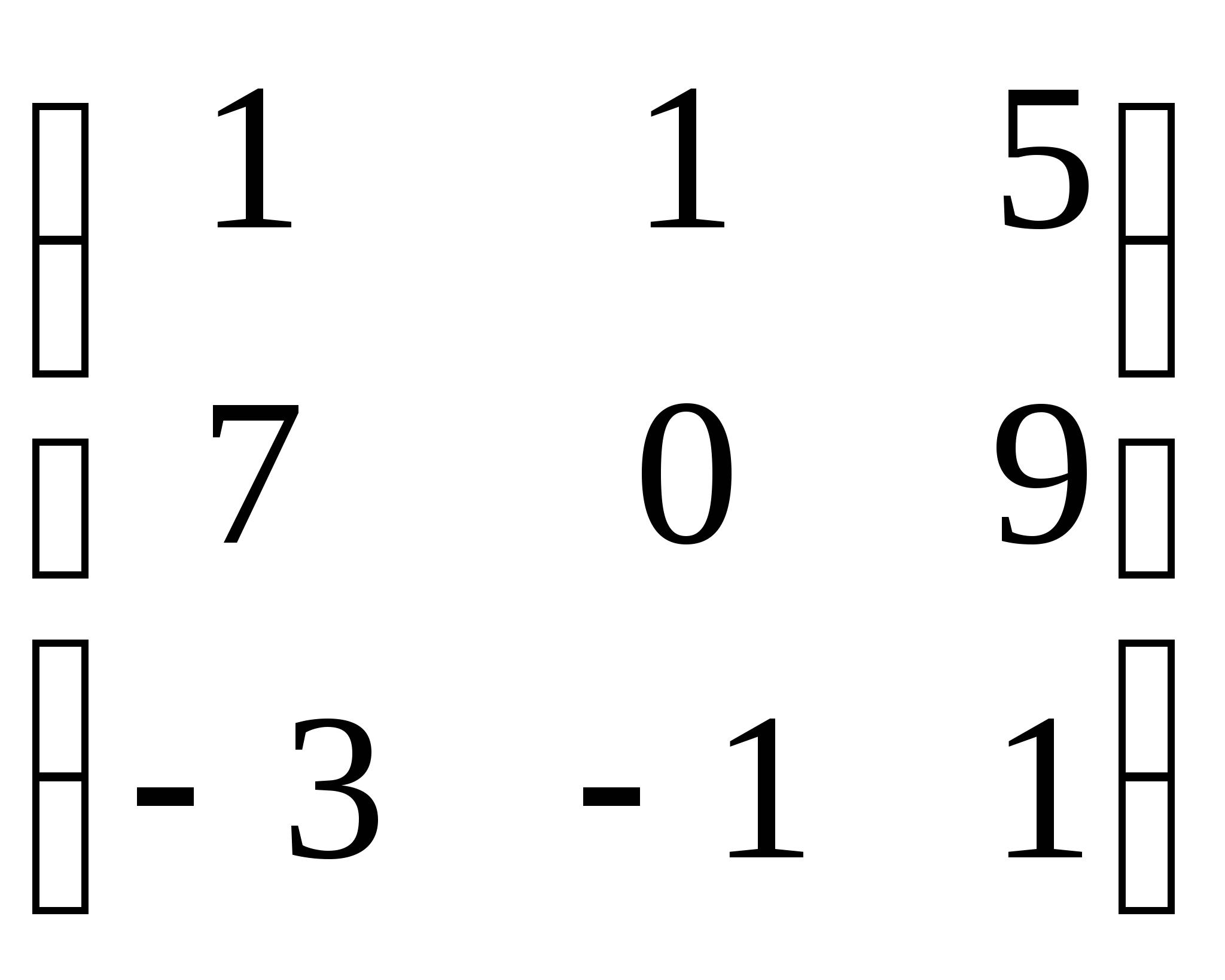
Чтобы вычесть из матрицы А матрицу В, надо к матрице А прибавить матрицу, противоположную матрице В.
А - В = А + (-В)
Пример 2: Найти разность матриц А - В: А =
![]() и В =
и В = ![]() .
.
Решение: С = А - В -В = ![]() С =
С = ![]()
Пример 3: Дана матрица А =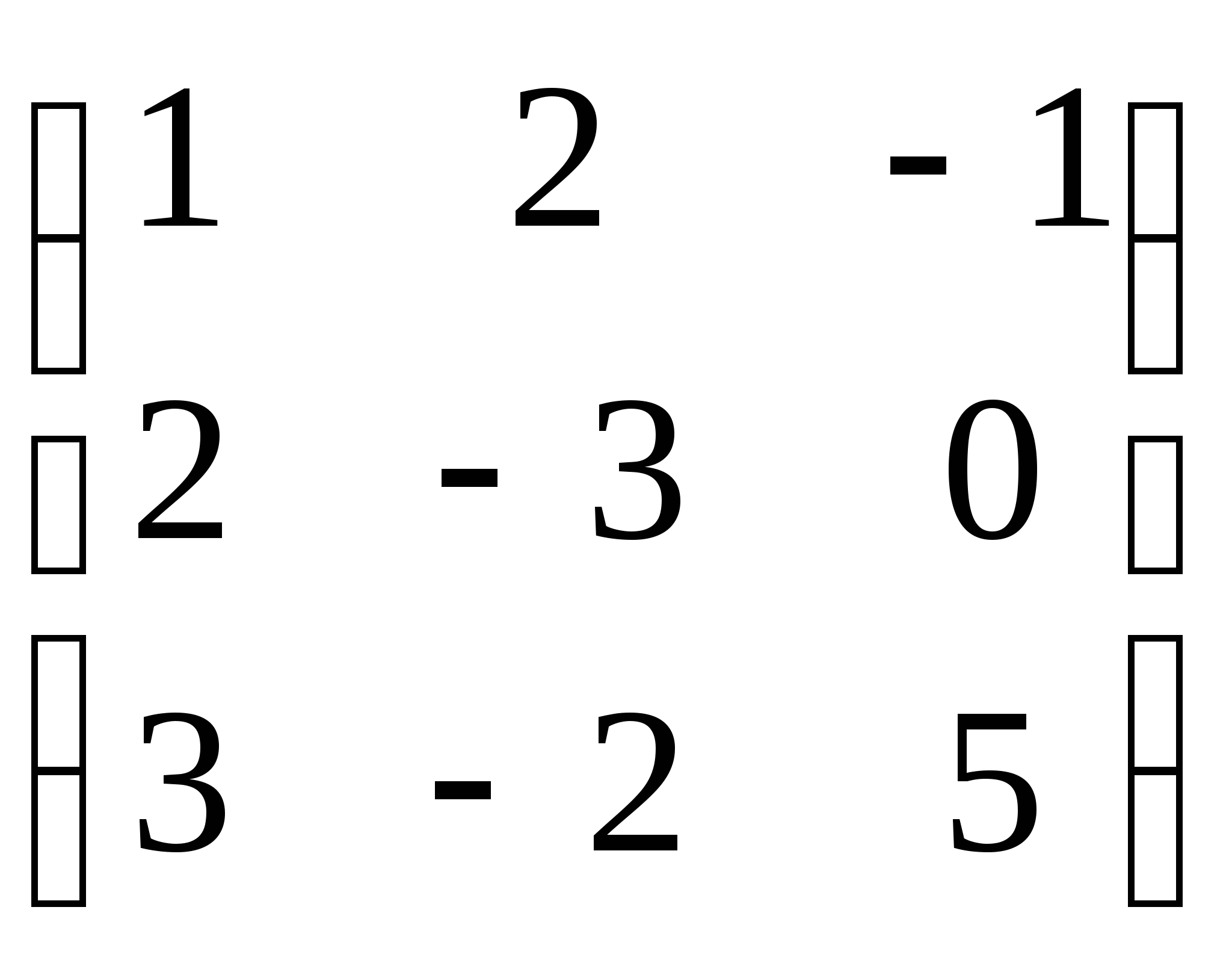 .
Найти матрицу С = 2А.
.
Найти матрицу С = 2А.
Решение: С = 2А = 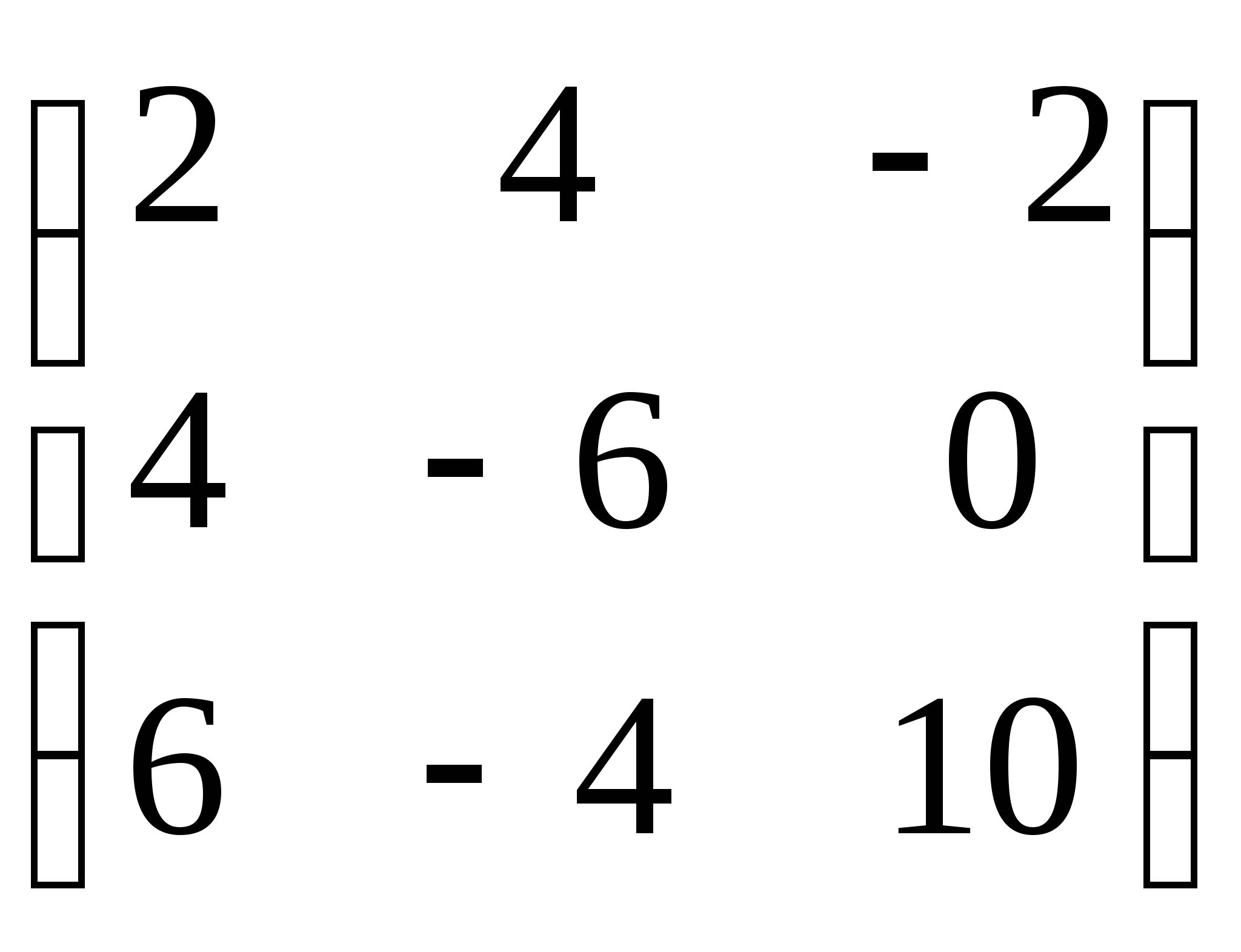
Пример 4: Даны матрицы: А = ![]() и В =
и В = ![]() .
.
Найти произведение матриц А и В.
Решение: С = АВ С = ![]() С =
С = ![]()
Задания для решения:
1.Вычислить произведение матриц:
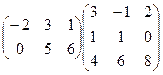 .
.
Решение. Первая матрица имеет размеры 2´3, а вторая размеры 3´3, поэтому произведение существует. В результате умножения получится матрица С = (cij) размеров 2´3. Вычислим ее элементы.
с11 = (-2)×3 + 3×1 + 1×4 = 1, с12 = (-2)×(-1) + 3×1 + 1×6 = 11,
с13 = (-2)×2+3×0+1×8 = 4, с21 = 0×3 + 5×1 + 6×4 = 29,
с22 = 0×(-1) + 5×1 + 6×6 = 41, с23 = 0×2+5×0+6×8 = 48.
Ответ: ![]() .
.
2.Вычислить произведение матриц:
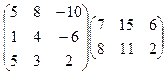 .
.
Решение. Первая матрица имеет размеры 3´3, а вторая размеры 2´3. Число столбцов в первой матрице (3) не совпадает с числом строк во второй матрице (2), поэтому произведение не существует,
Ответ: произведение не существует.
3.Вычислить произведение матриц:
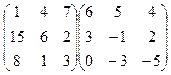 .
.
Ответ: 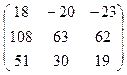 .
.
4.Вычислить произведение матриц:
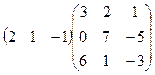 .
.
5.Вычислить произведение матриц:
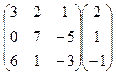 .
.
6.Вычислить произведение матриц:
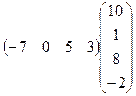 .
.
7.Вычислить произведение матриц:
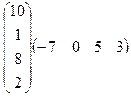 .
.
8.Вычислить произведение матриц:
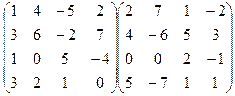 .
.
9.Вычислить степень матрицы:
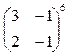 .
.
10. Вычислить степень матрицы:
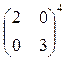 .
.
11. Вычислить значение многочлена f(x) =
2x2 + x - 3 от матрицы ![]() .
.
Указание. f(А) = 2А2 + А - 3Е, где Е - единичная матрица размеров 2´2. Далее использовать определения операций умножения матриц, умножения матрицы на число и сложения матриц.
Ответ: ![]() .
.
12. Вычислить значение многочлена f(x) = x3 - x2 + x + 2 от матрицы
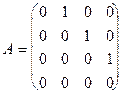 .
.
Ответ: 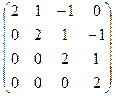 .
.
-
Итоги занятия.
Вопросы и задания для самооценки:
ЧТО НАЗЫВАЕТСЯ:
- матрицей, квадратной, единичной, диагональной, транспонированной
матрицей;
- обратной матрицей, рангом матрицы, базисным минором;
- определителем, минором, алгебраическим дополнением;
ПЕРЕЧИСЛИТЬ СВОЙСТВА:
- суммы матриц, произведения матрицы на скаляр, произведения
матриц;
- определителей.
ЗАПИСАТЬ ФОРМУЛЫ:
- для вычисления определителей второго и n-го порядка, для
нахождения обратной матрицы.
СФОРМУЛИРОВАТЬ
- существования и единственности обратной матрицы; теорему о
базисном миноре.
-
Домашнее задание. Учить определения, составить опорную схему конспекта. Выполнить упражнения:
1.Найти ![]() , если
, если 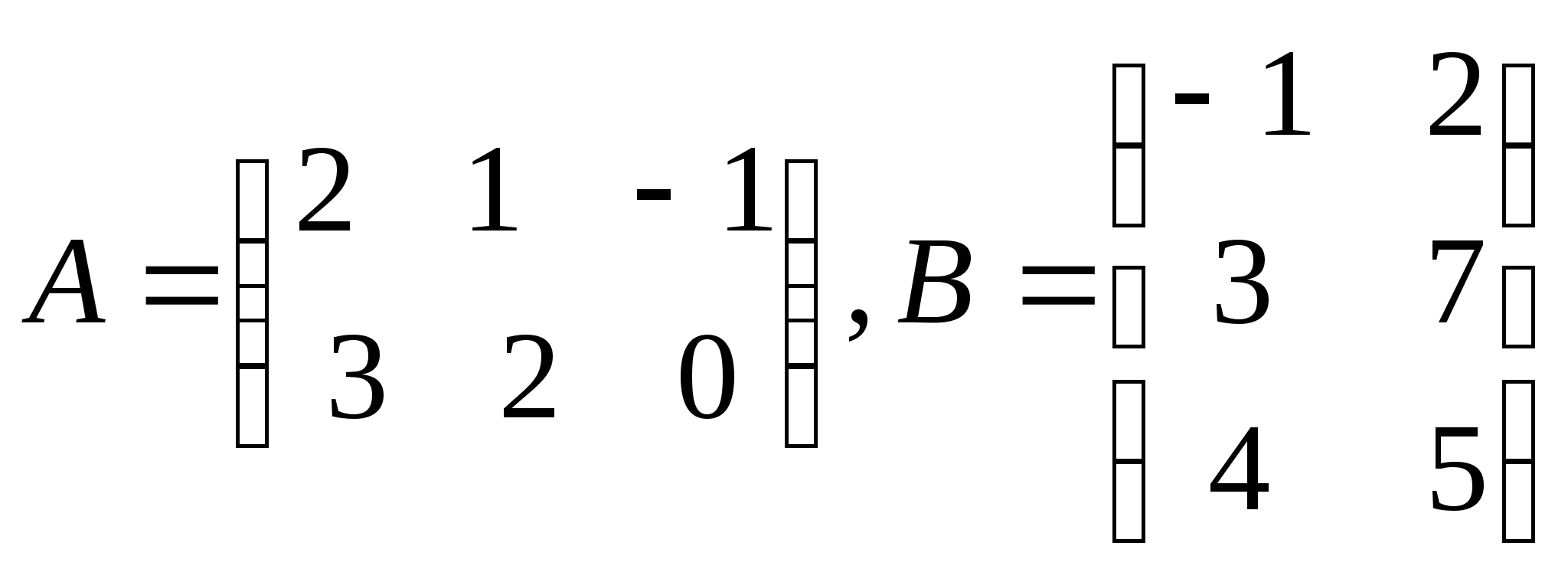 .
.
2.Даны матрицы 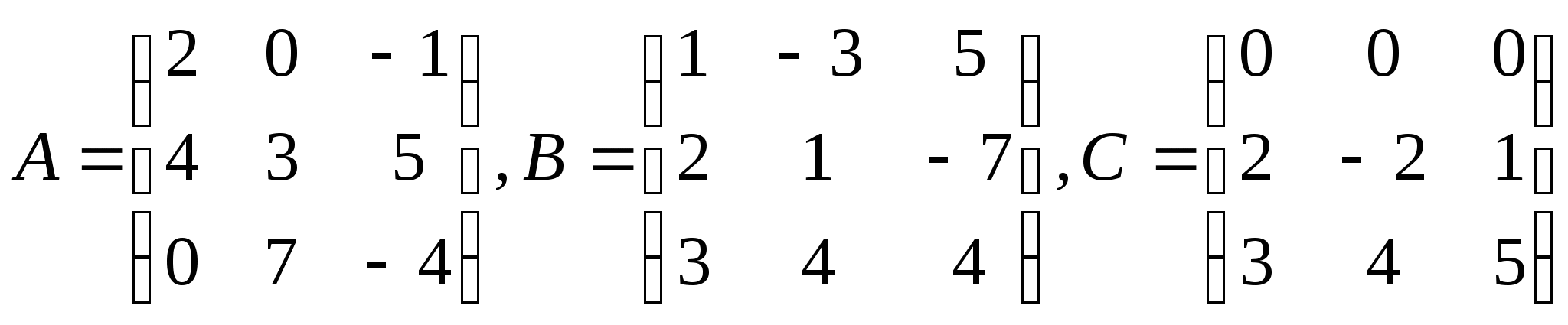 .
.
Найти: а) ![]() б)
б) ![]()
3.Найти матрицу ![]() , если
, если
а) 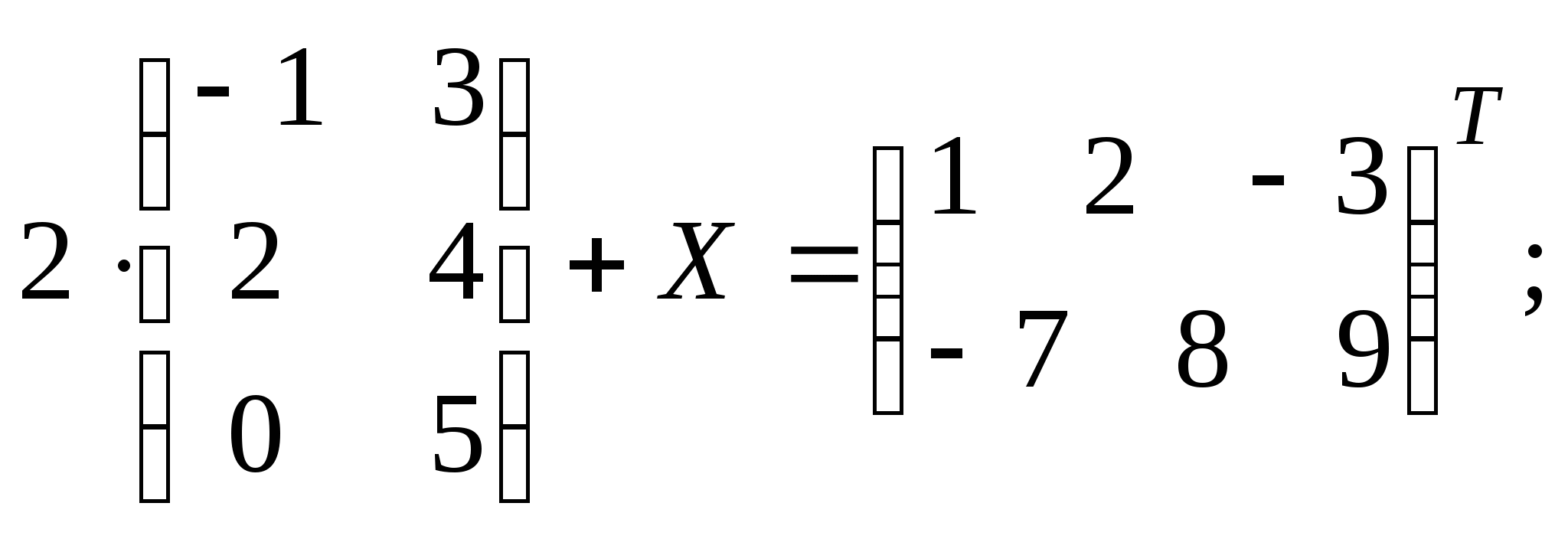
б) ![]()
-
Рефлексия.
Продолжи фразу
1. Я повторил …
2. Я узнал …
3. Я научился…
4. Я могу…
21