Геометрия 9 класс

Самостоятельная работа по теме:

«Простейшие задачи в координатах»

I вариант

1. Найдите координаты вектора 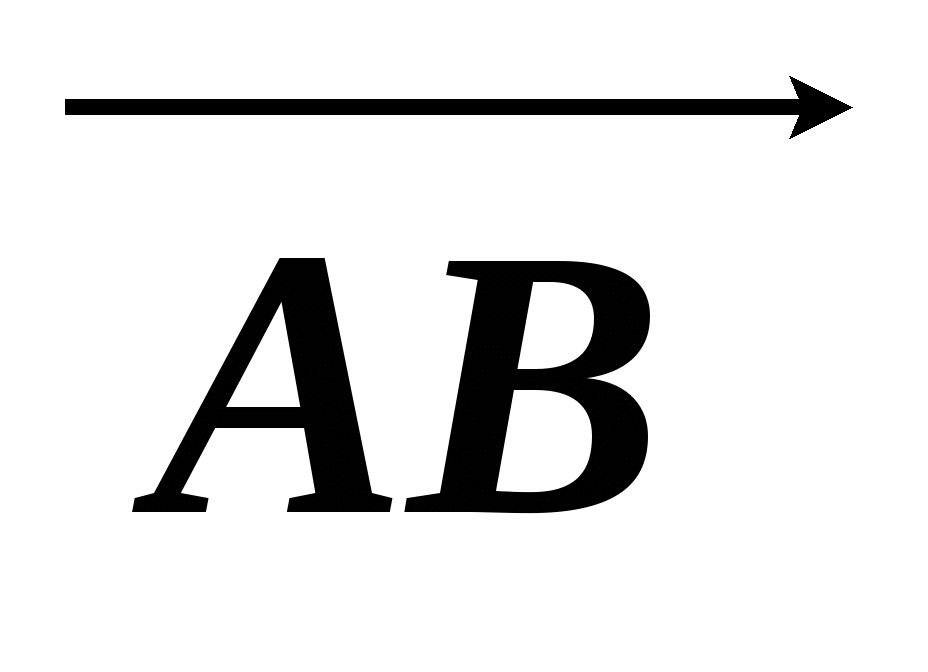, если А(-7; 6), В(-1; 2).

2. Найдите длину вектора 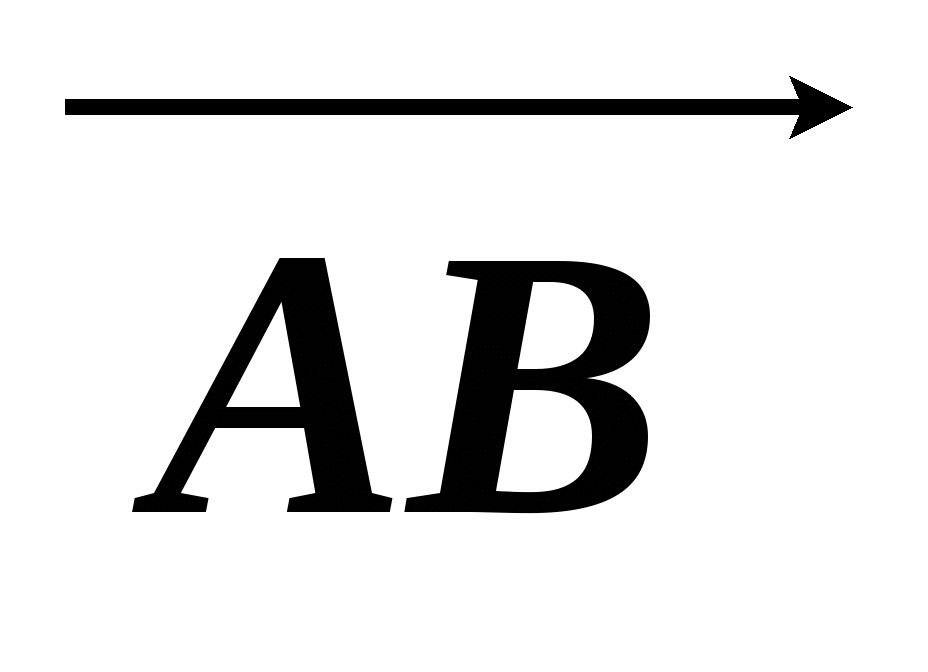, если А(-7; 6), В(-1; 2).

3. Найдите координаты точки К, которая является серединой отрезка MN , если М(6; -5), N(3; -9)

4. Найдите расстояние между точками M и N, т.е. длину отрезка MN, если М(6; -5), N(3; -9)

5. Найдите медиану CD треугольника АВС, вершины которого имеют координаты: А(-1; 2), В(5; -6), С(6; 4)

Геометрия 9 класс

Самостоятельная работа по теме:

«Простейшие задачи в координатах»

II вариант

1. Найдите координаты вектора 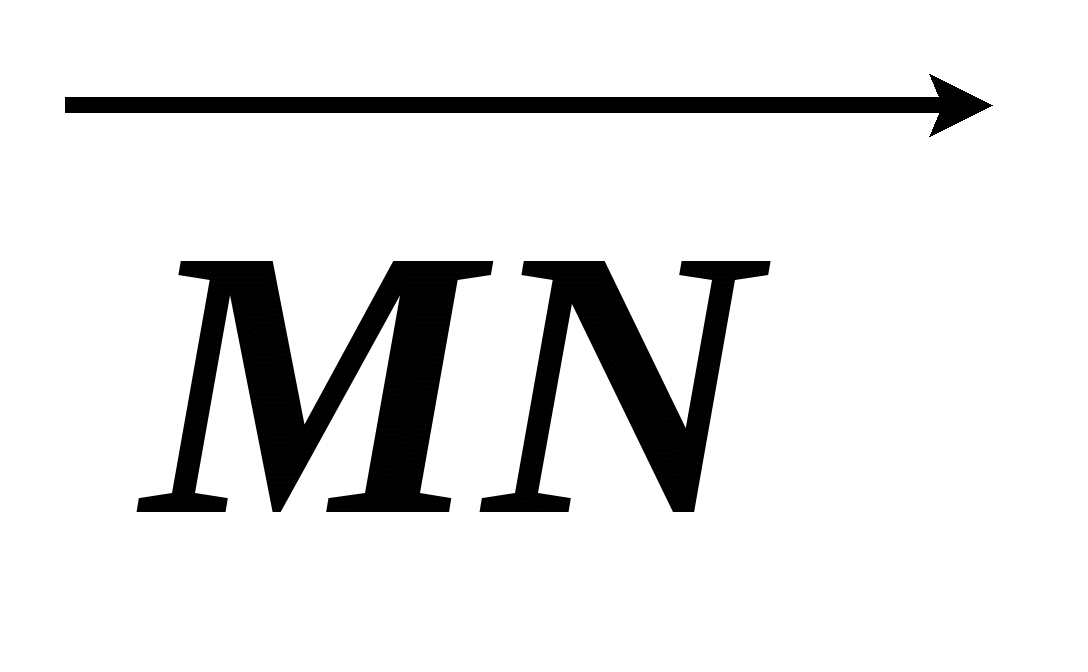, если M(4; -5), N(7; -9).

2. Найдите длину вектора 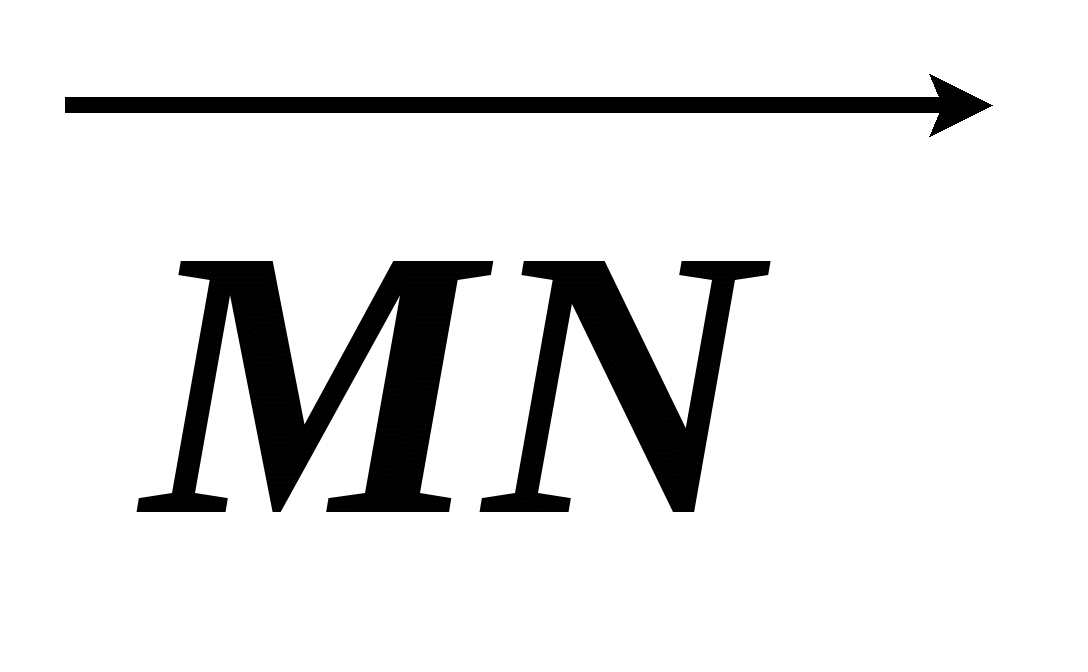, если M(4; -5), N(7; -9).

3. Найдите координаты точки C, которая является серединой отрезка AB , если A(-2; 1), B(-10; -5)

4. Найдите расстояние между точками A и B, т.е. длину отрезка AB, если A(-2; 1), B(-10; -5)

5. Найдите медиану BD треугольника АВС, вершины которого имеют координаты: А(-2; -3), В(-3; 5), С(4; 1)

Геометрия 9 класс

Самостоятельная работа по теме:

«Простейшие задачи в координатах»

III вариант

1. Найдите координаты вектора 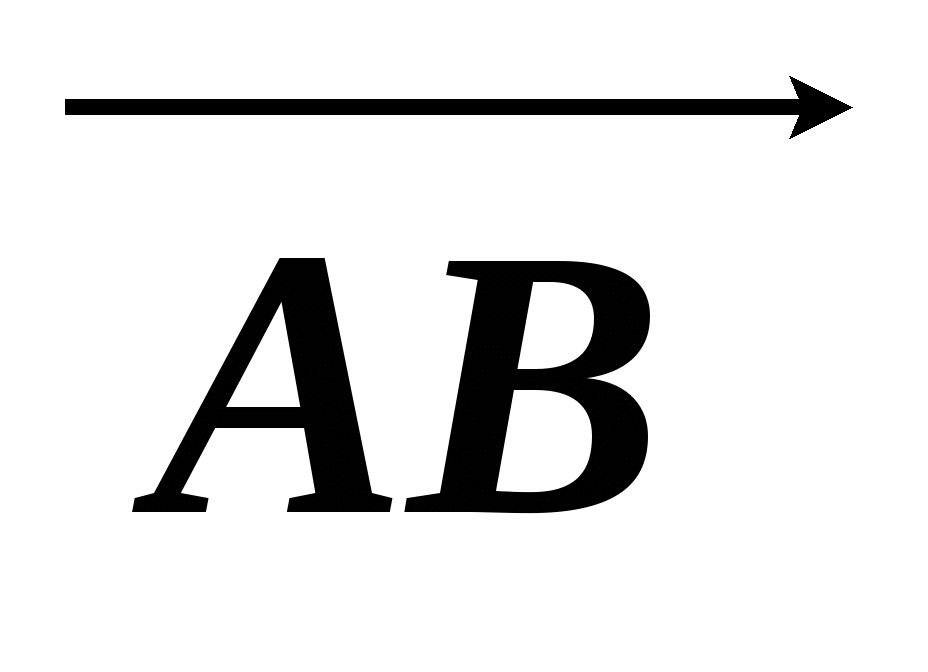, если А(8; -5), В(2; 3).

2. Найдите длину вектора 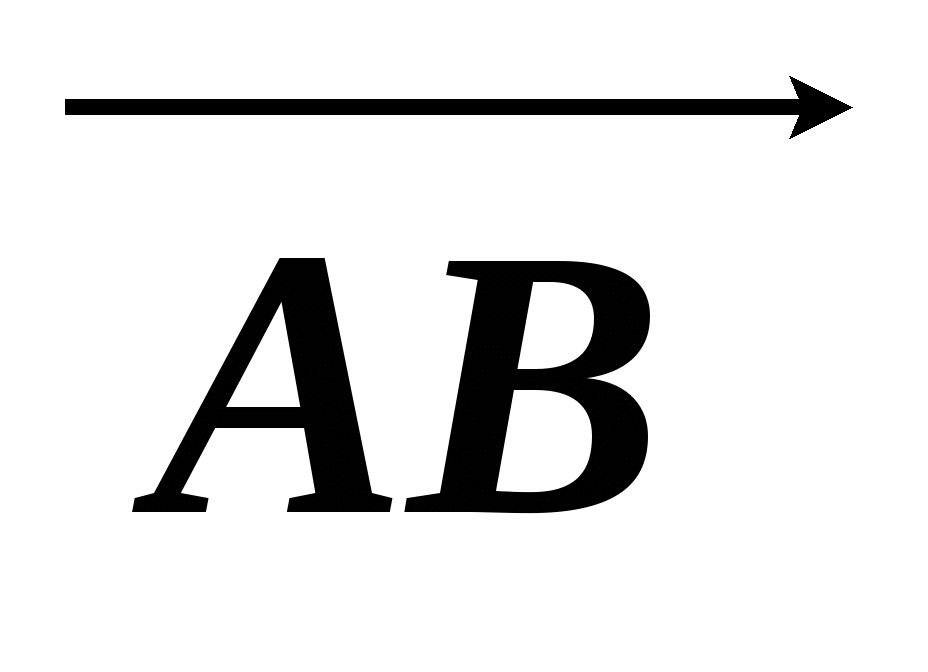, если А(8; -5), В(2; 3).

3. Найдите координаты точки К, которая является серединой отрезка MN , если М(1; -5), N(-2; -1)

4. Найдите расстояние между точками M и N, т.е. длину отрезка MN, если М(1; -5), N(-2; -1)

5. Найдите медиану AD треугольника АВС, вершины которого имеют координаты: А(2; 4), В(-5; -1), С(3; -5)

Геометрия 9 класс

Самостоятельная работа по теме:

«Простейшие задачи в координатах»

IV вариант

1. Найдите координаты вектора 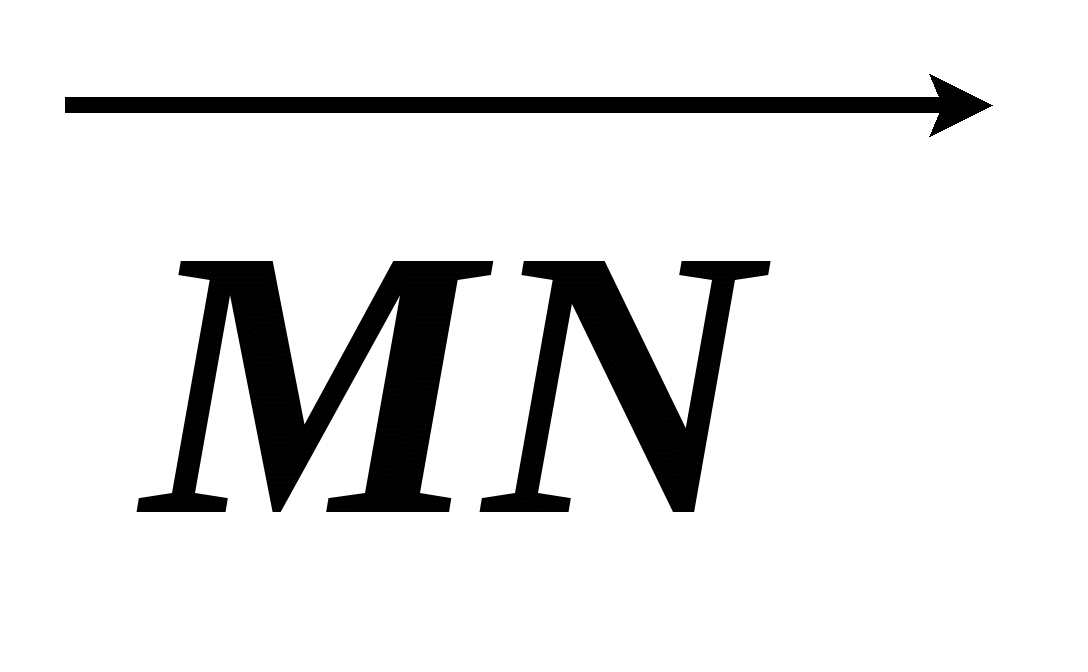, если M(-1; -7), N(2; -3).

2. Найдите длину вектора 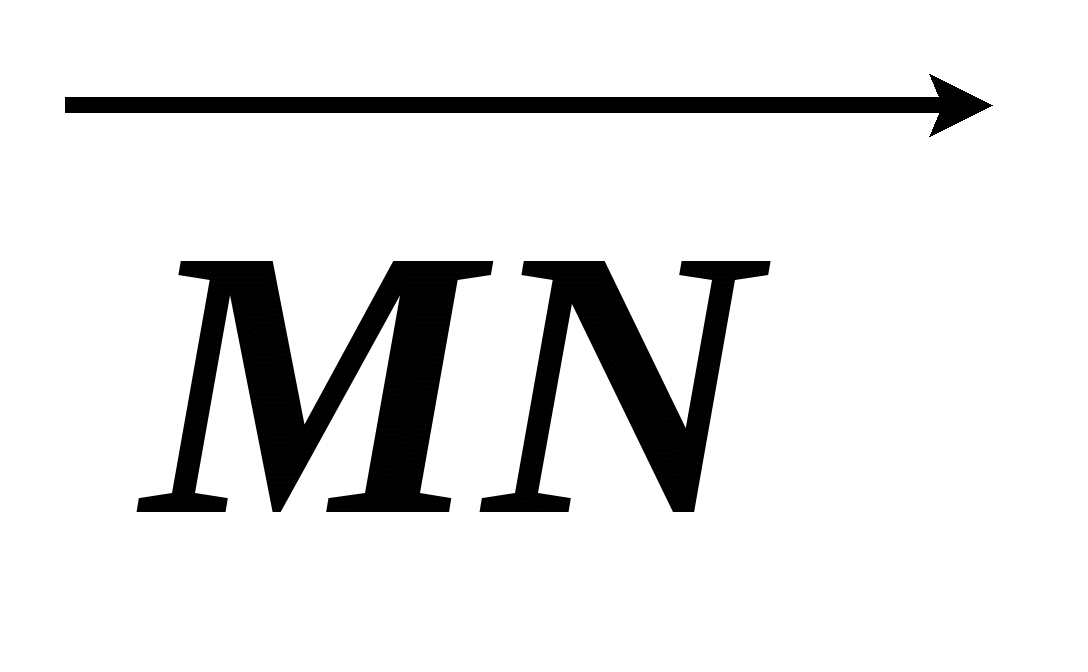, если M(-1; -7), N(2; -3).

3. Найдите координаты точки C, которая является серединой отрезка AB , если A(5; -4), B(-3; 2)

4. Найдите расстояние между точками A и B, т.е. длину отрезка AB, если A(5; -4), B(-3; 2)

5. Найдите медиану NP треугольника MNK, вершины которого имеют координаты: M(-4; 3), N(-3; -2), K(6; 1)