- Учителю
- Урок исследовательского обучения (8 класс)
Урок исследовательского обучения (8 класс)
Урок исследовательского обучения.
Формируем целеполагание у учащихся.
Урок алгебры в 8-м классе по теме «Иррациональные числа».
1 этап организации учебной деятельности: «Подготовка к исследованию».
Цель деятельности учителя: подвести учащихся к формулированию темы урока и осознанию цели урока.
Цель деятельности учащихся: сформулировать тему урока, осмыслить цели урока.
Описание процесса:
Учитель
Учащиеся
1 этап восприятия: (приём информации)
- Запись на доске:
ratio - разум (лат.),
«рациональные числа» - разумные числа, неразумные числа -«…?...».
- «Приведите пример, почему вы так решили?»
- «Так говорят в реальной жизни, но в математике не принято говорить нерациональное число, говорят «иррациональное число». Как вы думаете, с каким числами сегодня мы будем работать?»
2 этап восприятия информации: переработка информации.
-Предлагает решить задачи одинакового содержания, но с разными числами: «Найдите гипотенузу прямоугольного треугольника с катетами:
а) 3 см и 4 см; б) 1 см и 2 см»
-«Вы смогли выполнить задание полностью?»
- «В чём затруднение? Чем пункт а) не похож на пункт б)?»
- «Покажите запись, на которой остановились».
- Так выглядит иррациональное число.
3 этап восприятия: обработка информации
- «Попробуйте оценить, между какими числами находится число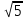 ».
».
-«Действительно, иррациональное число выражается бесконечной непериодической дробью: 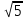 = 2,236…, или
= 2,236…, или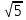 2,236».
2,236».
- «Попробуйте разбить предложенный ряд чисел на две группы (характеристику придумайте сами) и сделайте вывод: 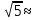 ».
».
-«Какова тема урока?»
4 этап восприятия: логический
«В каких других случаях встречаются иррациональные числа? Приведите примеры»
Интерес, желание угадать, отличиться (мотив различный)
- Наглядное восприятие записи на доске и догадки слова, которое можно поставить вместо многоточия: «нерациональное».
- «Решение рациональное - решение разумное», «Решение нерациональное - решение неразумное».
-С «иррациональными числами».
Трансформация информации в символы.
-а) Выполняют, находят ответ (5 см);
-б) испытывают затруднение в вычислении.
- «Нет, не смогли», «Смогли, но не полностью».
- «В первой задаче легко извлекается корень квадратный из числа 25. Во второй задаче не можем извлечь корень квадратный из числа 5».
- « 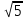 ».
».
- Добавляют в тетради запись:
« 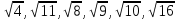 ».
».
Согласование сформированных символов с имеющимся опытом
- а) «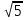 »;
»;
б) «2,2 »;
»;
в) «2,23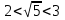 »;
»;
г) «2,236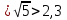 »…… так можно до бесконечности, так как нет повторяющихся фрагментов.
»…… так можно до бесконечности, так как нет повторяющихся фрагментов.
- «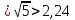 » - под знаком корня числа, которые являются точным квадратом чисел 2,3,4 соответственно;
» - под знаком корня числа, которые являются точным квадратом чисел 2,3,4 соответственно;
«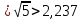 » - под знаком корня числа, которые не являются точным квадратом чисел.
» - под знаком корня числа, которые не являются точным квадратом чисел.
Вывод: если натуральное число nне являетсяточным квадратом, т.е.n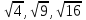 , где k
, где k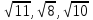 , то
, то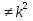 - иррациональное число».
- иррациональное число».
- «Иррациональные числа»
Осознание и аккомодация первично поступающей информации
- Приводят примеры, как из области математики, так и из жизненных ситуаций.
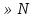 б) длина квадратной комнаты площадью 20
б) длина квадратной комнаты площадью 20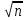 ».
».
2 этап организации учебной деятельности: «Исследование».
Цель деятельности учителя: формирование умения декомпозировать цель исследования на цели этапов исследования.
Цель деятельности учащихся: удерживая общую цель учебного исследования, переработать в ближайшие учебные задачи (в соответствии с этапами исследования) по её достижению.
Описание процесса:
Учитель
Учащиеся
1этап восприятия: (приём информации)
«Любая арифметическая операция над рациональными числами приводит в результате к рациональному числу. А как обстоит дело с иррациональными числами?»
2этап восприятия информации: переработка информации
«Все ли варианты примеров перебрали?»
(Забывают про 0)
«А если в операции участвуют одно рациональное, а другое иррациональное число, кто кого «пересилит»? Попробуйте доказать»
3 этап восприятия: обработка информации
« Вы рассмотрели четыре арифметических действия с иррациональными числами. В 7 классе мы научились возводить числа в степень. Как вы думаете, может ли число ab быть рациональным, если a и b --- иррациональные числа?»
4 этап восприятия: логический
«Расположите на координатной прямой числа: -3;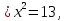 2,5;
2,5; 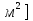 ;
;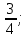 , 8.
, 8.
Сделайте вывод».
Познавательный интерес -возникновение вопросов, побуждающих к действию (мотив различный)
1)«Проверить на примерах что получится при сложении, вычитании, умножении и делении иррациональных чисел?
2)Достаточно ли по одному примеру на каждое действие, чтобы сделать вывод?»
Трансформация информации в символы
Придумывают неповторяющиеся по структуре примеры: а)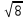 б)
б)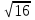 ; в)
; в)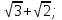 =
=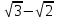 ; г)
; г)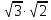 = 3; д)
= 3; д)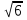 =
= 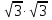 ; е)
; е)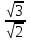 = 1;
= 1;
Делают вывод: «В ответе может получиться как рациональное, так и иррациональное число».
Добавляют поправку к выводу: действие с 0.
Выбирают путь решения задачи:1) перебор вариантов примеров различных комбинаций; 2) пытаются доказать методом от противного (после подсказки учителя).
Делают вывод: «Результат иррациональное число (кроме умножения и деления на 0).
Согласование сформированных символов с имеющимся опытом
-Рассуждают самостоятельно: если подставить иррациональные числа вместо a и b, то ответ отрицательный.
-Рассуждают с помощью учителя: а если усложнить внешний вид иррационального числа? Как? Вспоминают свойство степеней (возведение степени в степень); соотносят с результатом умножения двух одинаковых иррациональных чисел. Делают вывод:
«Рассмотрим число 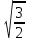
![]() . Если это число рациональное, то задача решена:a и b найдены. Если же оно иррациональное, то возьмем a=
. Если это число рациональное, то задача решена:a и b найдены. Если же оно иррациональное, то возьмем a=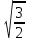
![]() , b=
, b=![]() , и ab=(
, и ab=(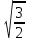
![]() )
)![]() =3. Ответ: да».
=3. Ответ: да».
Осознание и аккомодация первично поступающей информации
Выполняют задание, испытывают затруднение с 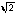 , но приблизительно отмечают верно. Вывод: иррациональному числу, также как и рациональному числу соответствует точка на координатной прямой. Координатная прямая и числовая прямая взаимозаменяемые термины. Для изображения иррационального числа нужен способ его оценивания и сравнения с другими числами.
, но приблизительно отмечают верно. Вывод: иррациональному числу, также как и рациональному числу соответствует точка на координатной прямой. Координатная прямая и числовая прямая взаимозаменяемые термины. Для изображения иррационального числа нужен способ его оценивания и сравнения с другими числами.
3 этап организации учебной деятельности: «Анализ исследования».
Цель деятельности учителя: формирование осознанной познавательной активности, удержание дидактической цели.
Цель деятельности учащихся: осознание места изучаемого материала в системе знаний, и личной значимости его успешного усвоения.
Описание процесса:
Учитель
Учащиеся
1этап восприятия: (приём информации)
«Что нового, важного вы открыли для себя, выполняя учебное исследование?»
Ориентируясь на ответы учащихся, организует полилог.
2этап восприятия информации: переработка информации
«Всё ли у всех получилось?»
3 этап восприятия: обработка информации
Задание.
а) «Докажите, что сумма рационального числа 3 и иррационального числа 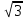 является числом иррациональным»;
является числом иррациональным»;
4 этап восприятия: логический
Систематизирует «открытия» с помощью вопросов.
Желание быть услышанным, самоуважение, уважение к ответам одноклассников
Высказываются, обсуждая и новые правила, и новые термины, и взаимосвязи, и технологии решений, и др.
Трансформация информации в символы.
Воспроизводят алгоритмы решения, обсуждают затруднения, предлагают альтернативные варианты.
Согласование сформированных символов с имеющимся опытом
Пользуясь изученным ранее понятием рационального числа, вновь изученным понятием иррационального числа с помощью метода доказательства от противного доказывают этот факт, осмысливая и закрепляя новые знания.
Осознание и аккомодация первично поступающей информации
Осмысливают в полном объёме «открытия»
4 этап организации учебной деятельности: «Контроль результатов первичного закрепления знаний. Оценка значимости полученного нового знания, включение в систему новых знаний».
Цель деятельности учителя: формирование умения самоконтроля и самооценивания у учащихся.
Цель деятельности учащихся: по результатам исследовательской деятельности оценить собственный уровень освоения способов, выявить неясные моменты, поставить задачи коррекции знаний.
Описание процесса:
Учитель
Учащиеся
1этап восприятия: (приём информации)
Выполните самостоятельно:
а) №1062,№1064,№1065;
б) Построить отрезки длиной 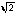
2этап восприятия информации: переработка информации
«Всё ли получилось?»
3 этап восприятия: обработка информации
Напоминает: « число - объект алгебры, отрезок - объект геометрии». Подсказка: «Вспомните теорему Пифагора и теорему о среднем пропорциональном отрезке».
4 этап восприятия: логический
«В чём испытывали затруднения?»
Блиц-опрос.
Мотивация к самостоятельной работе, желание убедиться, что новое знание освоено
Планируют шаги и выбирают уровень выполнения задания.
Трансформация информации в символы.
Выполняют самостоятельно задание.
Алгоритм решения, правила проговаривают вслух, комментируют решения, обсуждают ошибки, вариант построения: с помощью параболы и прямой.
Согласование сформированных символов с имеющимся опытом
Выполняют геометрическую интерпретацию иррациональных чисел. Делают вывод о единстве областей математики.
Осознание и аккомодация первично поступающей информации
Формулируют свои проблемы и цели коррекции знаний
5 этап организации учебной деятельности: «Исторические сведения. Подготовка учащихся к самостоятельному мини-исследованию».
Цель деятельности учителя: мотивация учащегося к включению в дальнейшую познавательную деятельность.
Цель деятельности учащихся: самоопределение
Описание процесса:
Учитель
Учащиеся
1этап восприятия: (приём информации)
Экскурс в историю: «Число «π»».
Презентация на экране.
2этап восприятия информации: переработка информации
Задание.
«Попробуйте по памяти воспроизвести число π»
Знакомит с мнемоническими правилами.
Например: «Это я знаю и помню прекрасно» (количество букв соответствует цифрам числа Пи); или: «Чтобы вам не ошибиться, надо правильно прочесть: 3; 14;15;92 и 6» (цифры запоминаются в стихотворной форме быстрее)
3 этап восприятия: обработка информации
Предлагается несколько задач геометрического содержание с использованием числа π.
4 этап восприятия: логический
Обсуждаются темы возможных мини - проектов по теме
Любопытство, удивление, изумление (количество знаков после запятой)
Трансформация информации в символы.
Показывают 3,14, дальше испытывают затруднения.
Пробуют составить четверостишия для запоминания цифр числа Пи: «Надо только постараться и запомнить всё как есть: «3; 14;15;92 и 6», или: «Можно просто постараться и почаще повторять: 3; 14;15;9; 26 и 5».
Согласование сформированных символов с имеющимся опытом
Выполняются задачи с вычислением результата после подстановки приближенного значения числа π (округление варьируется)
Осознание и аккомодация первично поступающей информации
Принимается решение о выполнении мини-проекта
6 этап организации учебной деятельности: «Рефлексия учебной деятельности (итог)».
Цель деятельности учителя: формирование у учащихся самооценивания собственных достижений результата поставленной цели и постановки дальнейшей цели.
Цель деятельности учащихся: планирование дальнейших целей деятельности.
Описание процесса:
Учитель
Учащиеся
1этап восприятия: (приём информации)
Предлагает учащимся выполнить дома следующее задание: п.27, №1068, творческое: мини-проект.
2этап восприятия информации: переработка информации
Есть ли вопросы по «Домашнему заданию»?
3 этап восприятия: обработка информации
Формирует банк тем проектных работ
4 этап восприятия: логический
Оценивает деятельность учащихся на уроке, их личностные достижения, прогнозирует дальнейшие действия
Устойчивая мотивация, внимание
Знакомятся с содержанием «Домашнего задания»
Трансформация информации в символы.
Проговаривают алгоритм выполнения задания, уточняют подходы к решению, записи решения, предлагают темы проекта.
Согласование сформированных символов с имеющимся опытом
Задают вопросы по технологии создания и презентации проекта.
Осознание и аккомодация первично поступающей информации. Соотносят оценивание учителя с самооценкой, планируют дальнейшую деятельность
Такой подход поможет учителю сконцентрировать усилия на главном. Учитель не только выделяет и конкретизирует цели, но и упорядочивает их, определяя задачи, порядок и перспективы дальнейшей работы. Совместная работа учителя и учеников предполагает ясность и гласность. Конкретные учебные цели дают возможность разъяснить учащимся ориентиры учебной работы, обсудить их. Обращение к четким формулировкам целей, которые выражены через результаты деятельности, поддается более объективной оценке.