Справочные материалы по теме Показательные уравнения и неравенства

Показательная функция, показательные уравнения и неравенства.

Определение: Функция, заданная формулой у = а^х, где а>0 и а≠1, называется показательной функцией с основанием а.

Основные свойства показательной функции: 1) а⁰ = 1; 2) а ^-х =; 3) а ^х а ^у=а ^{х+ у}; 4) ;

5) (аb)^х = а ^х b ^х; 6) ; 7) (а^х) ^у = а ^ху; 8) если а ^х=а ^у, то х=у;

9) при а>1 из условия, что а ^х > а ^у следует, что х > у;

при 0 < а < 1 из условия, что а ^х > а ^у следует, что х < у.

Показательные уравнения.

1) Простейшие а ^х=b, где а>0 и а≠1

Если b≤0, то корней нет, т.к. а ^х >0.

Если b >0, то х=log_a b.

1)

или .

2)

2) а ^f(x)=a ^g(x)  f(x)=g(x)

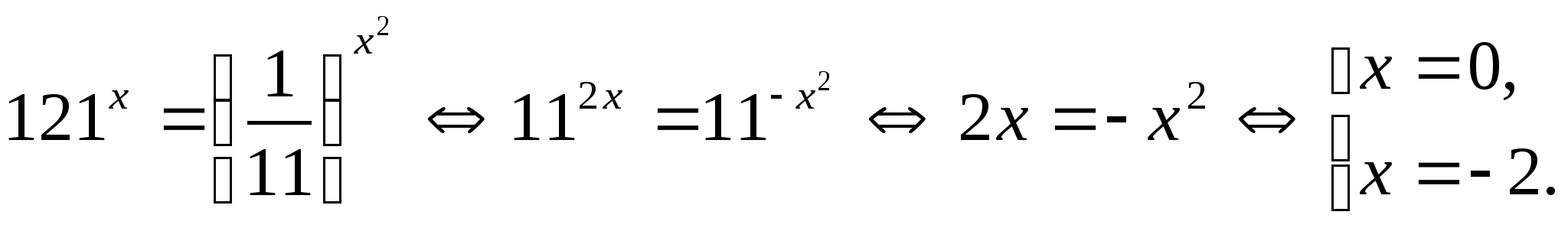
3) А а^{х+ т}+ В а^{х+ п}=С.

Выносим общий множитель а^х за скобки (за скобки можно выносить степень с наименьшим показателем).

4) А× а ^2х + В× а ^х =С.

С помощью замены а ^х = t приводим уравнение к квадратному А× t ²+ В× t =С.

5) А× а^х + В× а ^-х + С = 0.

С помощью замены а ^х = t приводим уравнение к квадратному А×t²+С×t +В=0.

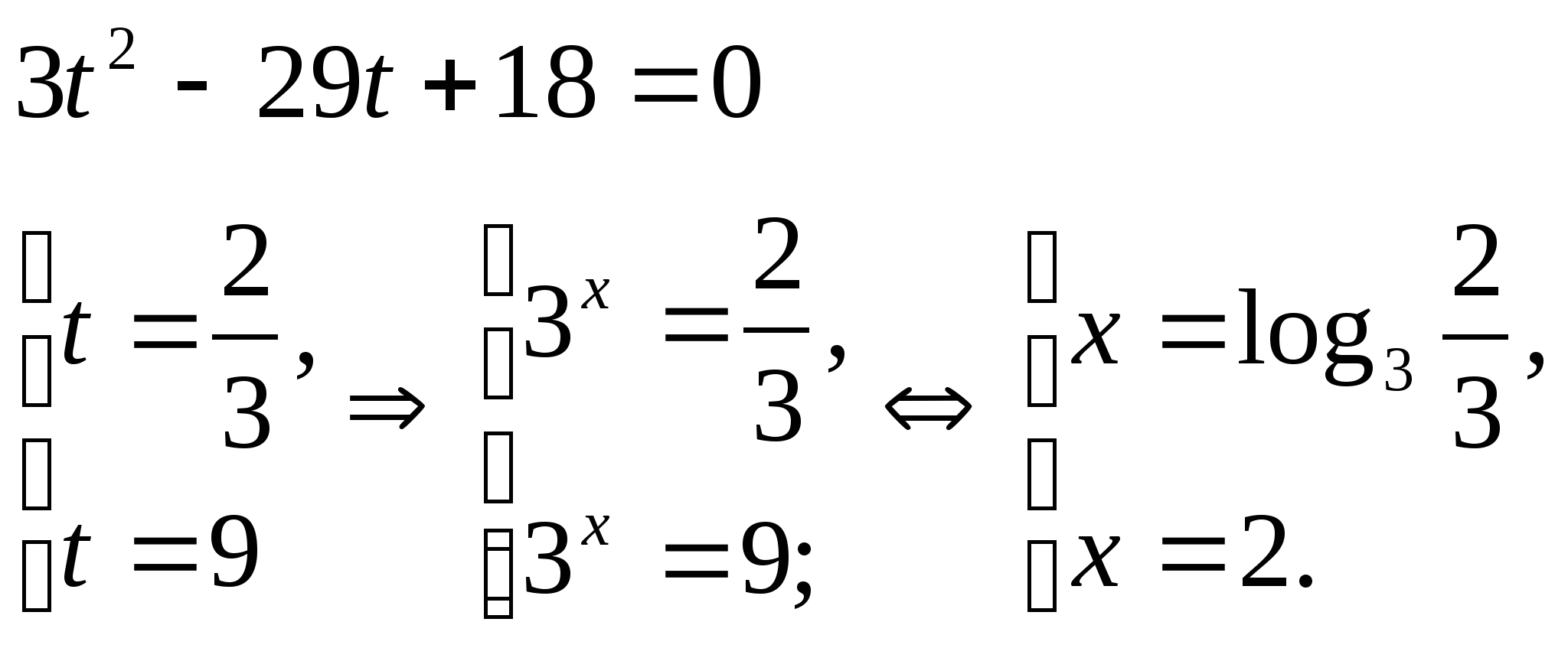
6) Однородные показательные уравнения:

А× а^х = В× b^х - 1 степени;

А× а ^2х+ В× а^х b^х+ С b^2х=0 - 2 степени;

А× а ^пх+ В× а^{т х} × b^(п-т)х +С×b^пх=0.

Решаем делением на b^х; b^2х; b^пх соответственно, т.к. b^х≠0, b^2х≠0, b^пх ≠0.

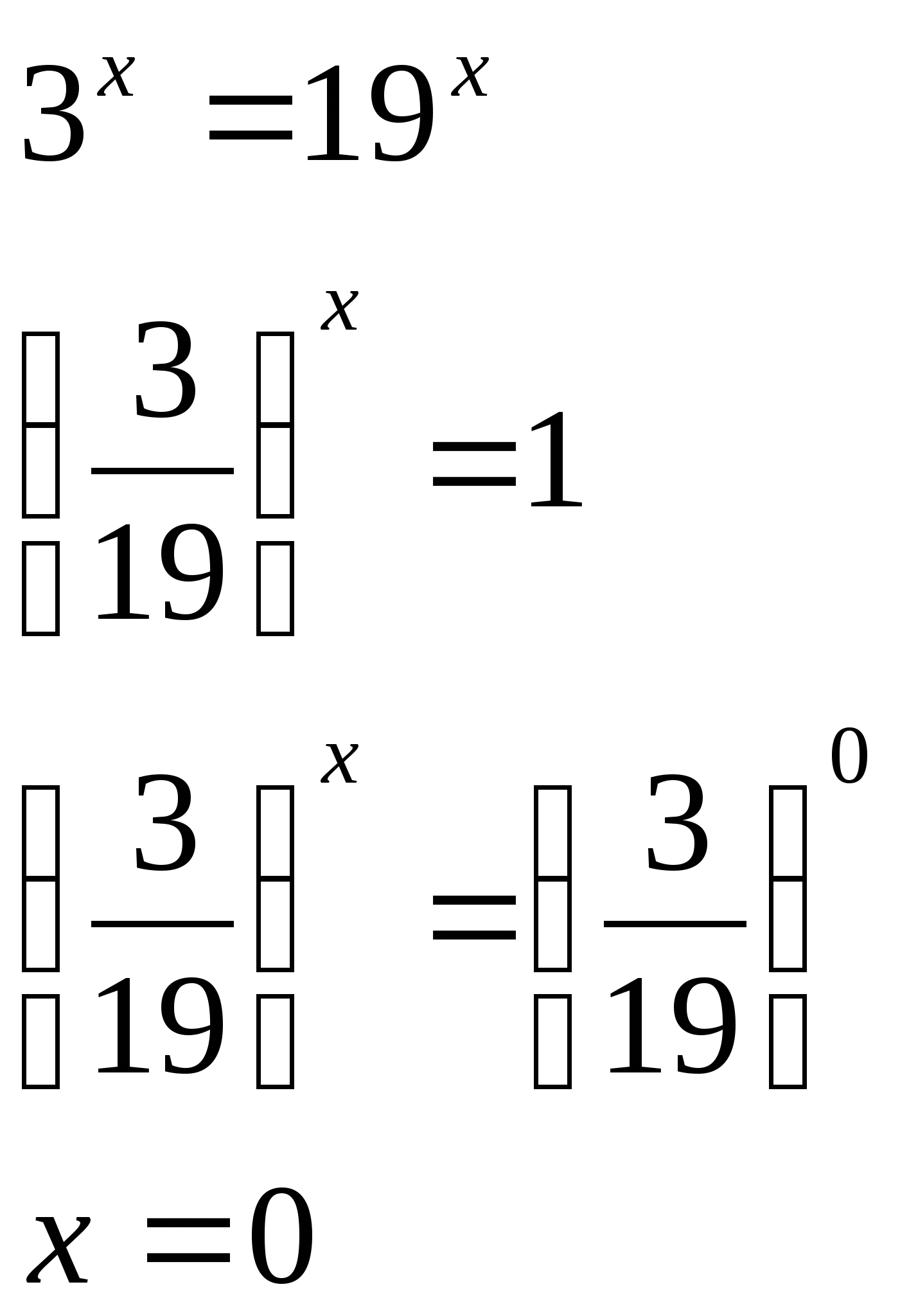
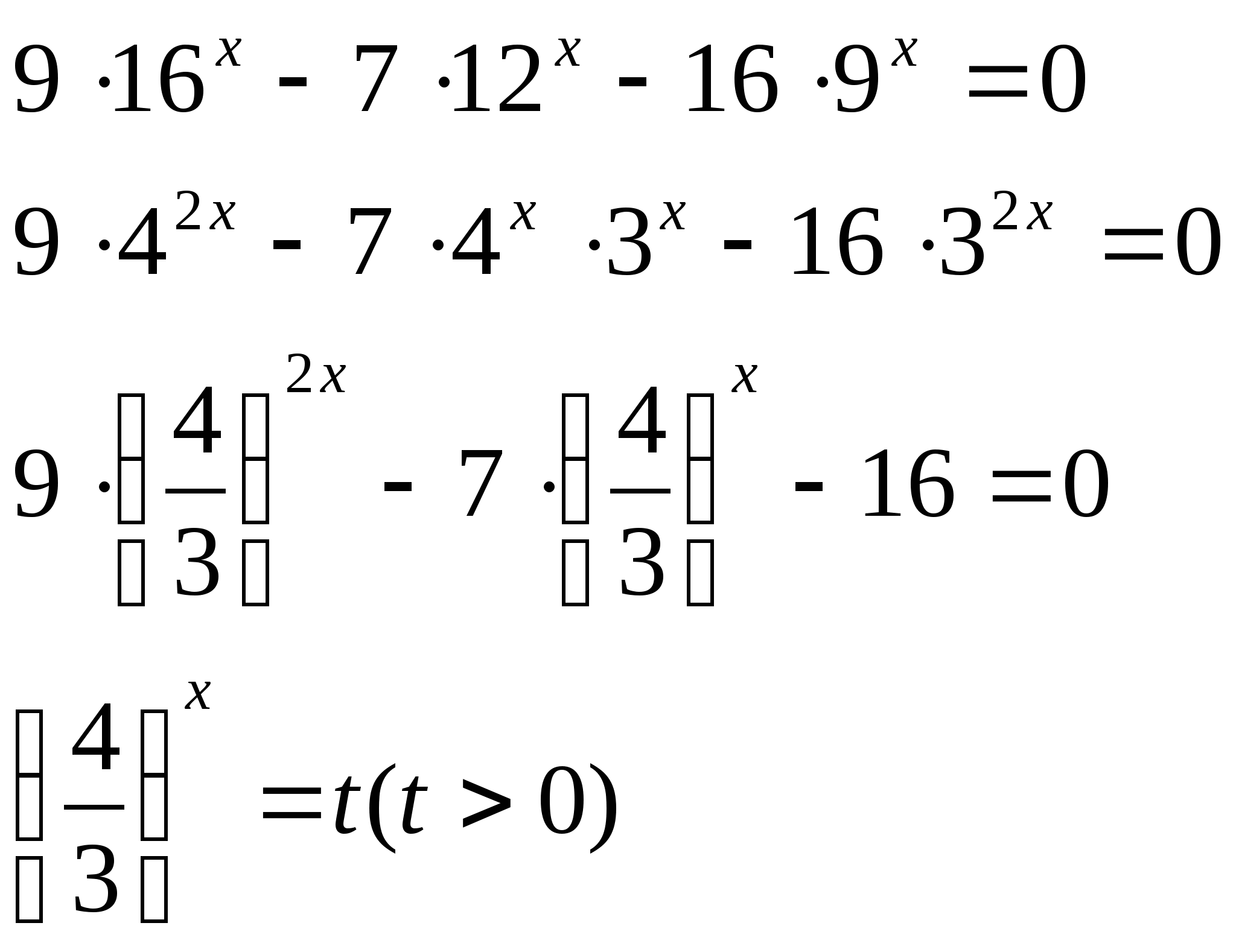
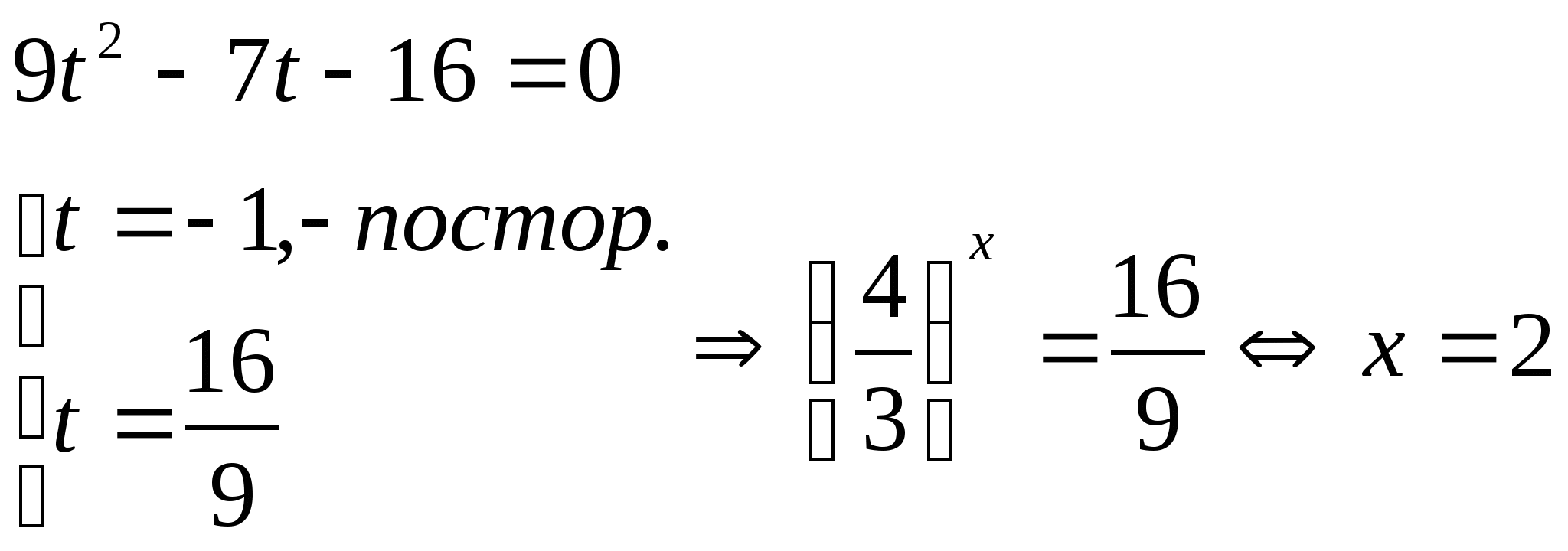
7) А × а ^f(x)=В × b ^g(x)

Логарифмируем обе части уравнения по одному и тому же основанию (в качестве основания логарифма можно взять, в том числе, а или b).

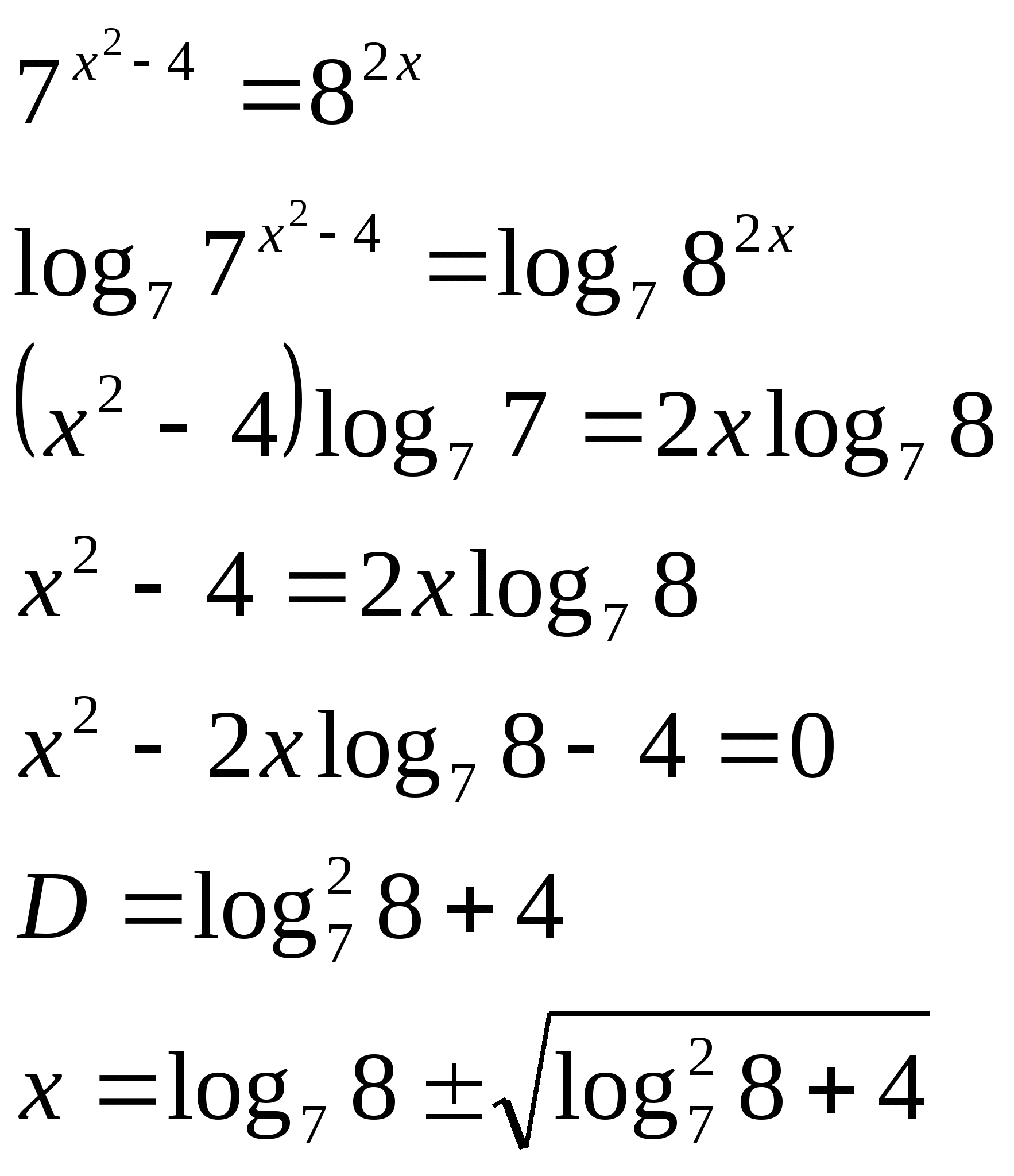
8) M, где а²- b=1. С помощью замены или приводим к квадратному

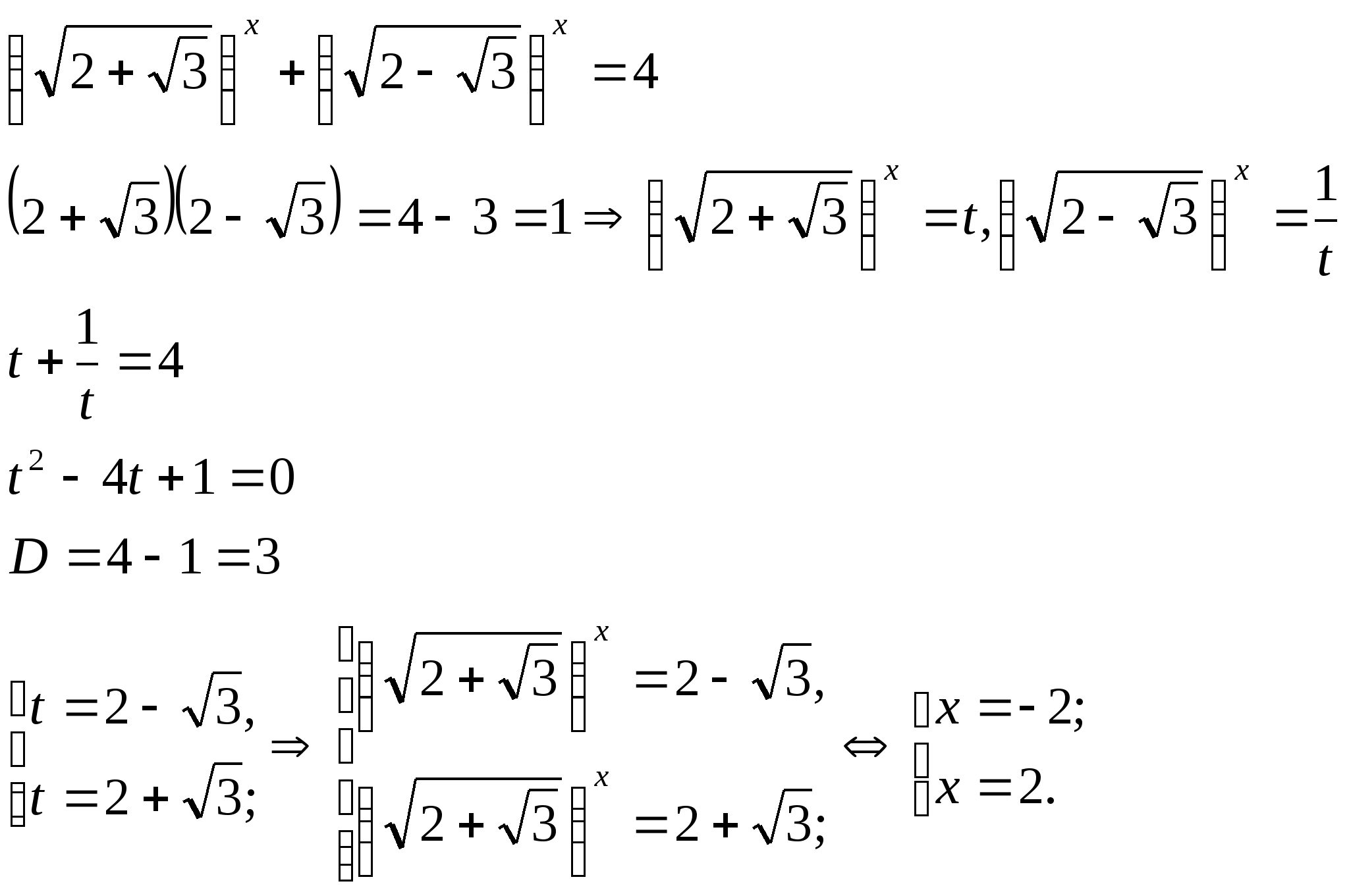
9) Уравнения, приводимые к алгебраическим уравнениям высших степеней.

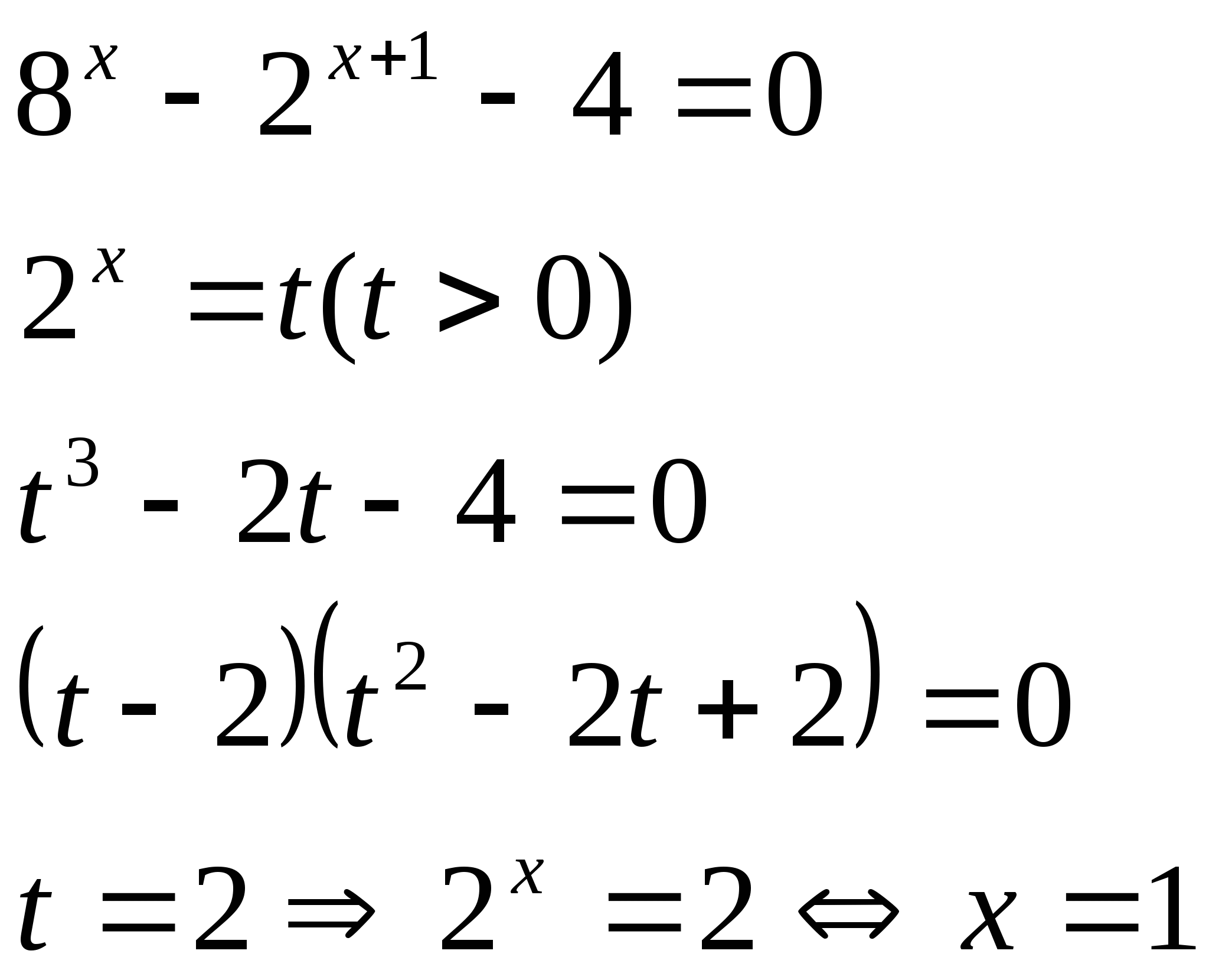
10) Уравнения, решаемые на основе свойств функций.

. Разделим обе части уравнения на 8^х:

. Выражение, стоящее в левой части равенства, задаёт убывающую функцию (т.к. основание меньше 1), а выражение, стоящее в правой части равенства, задаёт возрастающую функцию (т.к. основание больше 1). Следовательно, если корень существует, то он один. Подбором получаем, что х=2

Получаем, что основными способами решения показательных уравнений являются:

1. Метод уравнивания показателей степеней.

2. Функционально-графический (основан на использовании графических иллюстраций или свойствах функций)

3. Метод логарифмирования.

4. Метод введения новой переменной.

5. Метод разложения на множители.

6. Комбинированный.

Показательные неравенства.

Простейшие показательные неравенства имеют вид а^х > b или а^х < b.

а^х > b если b≤0, то х(-∞;+∞) а^х < b если b≤0, то хÎØ

если b > 0, то а^х > . если b > 0, то а^х < .

Тогда при а > 1 х > log_ab, Тогда при а > 1 х < log_ab,

при 0 < а < 1 х < log_ab при 0 < а < 1 х < log_ab.

Основные методы решения показательных неравенств те же, что и для уравнений. Полученные при этом простейшие неравенства решаются на основе вышеизложенного.

Степенно-показательные уравнения

Степенно-показательными уравнениями называются уравнения вида .

При решении уравнений данного типа важно учитывать следующие условия:

1. основание степени не может быть отрицательным.

2. рассматриваются два случая решения:

а) основание степени положительно;

б) основание степени равно 1, показатели степени при этом определены.

Степенно-показательные уравнения можно решать по следующей схеме:

1. Уравнения вида :

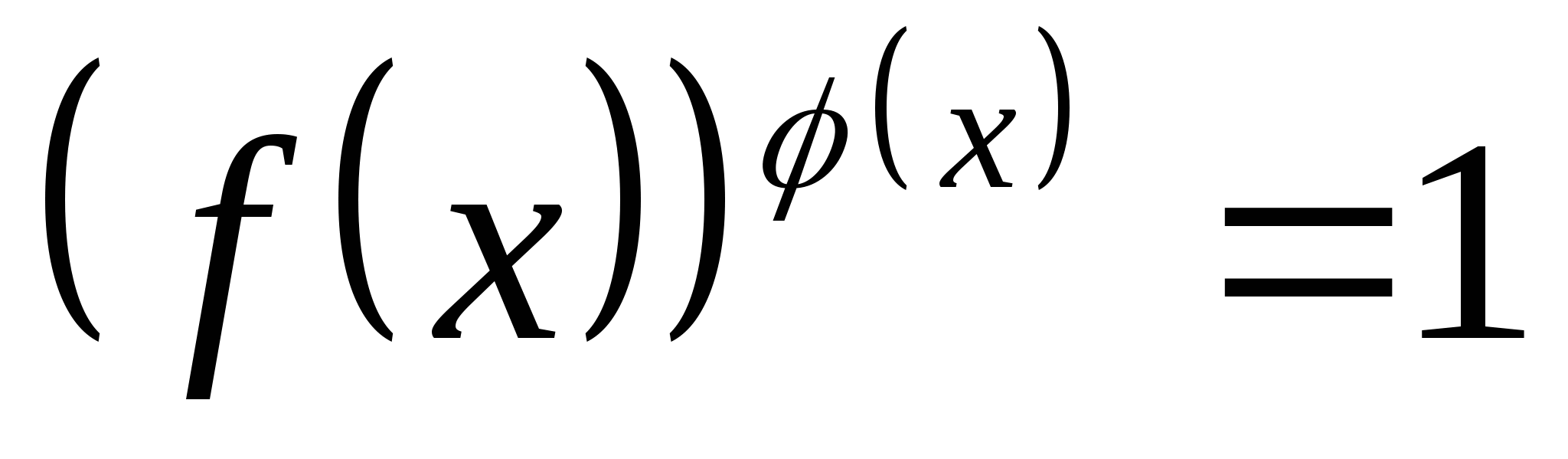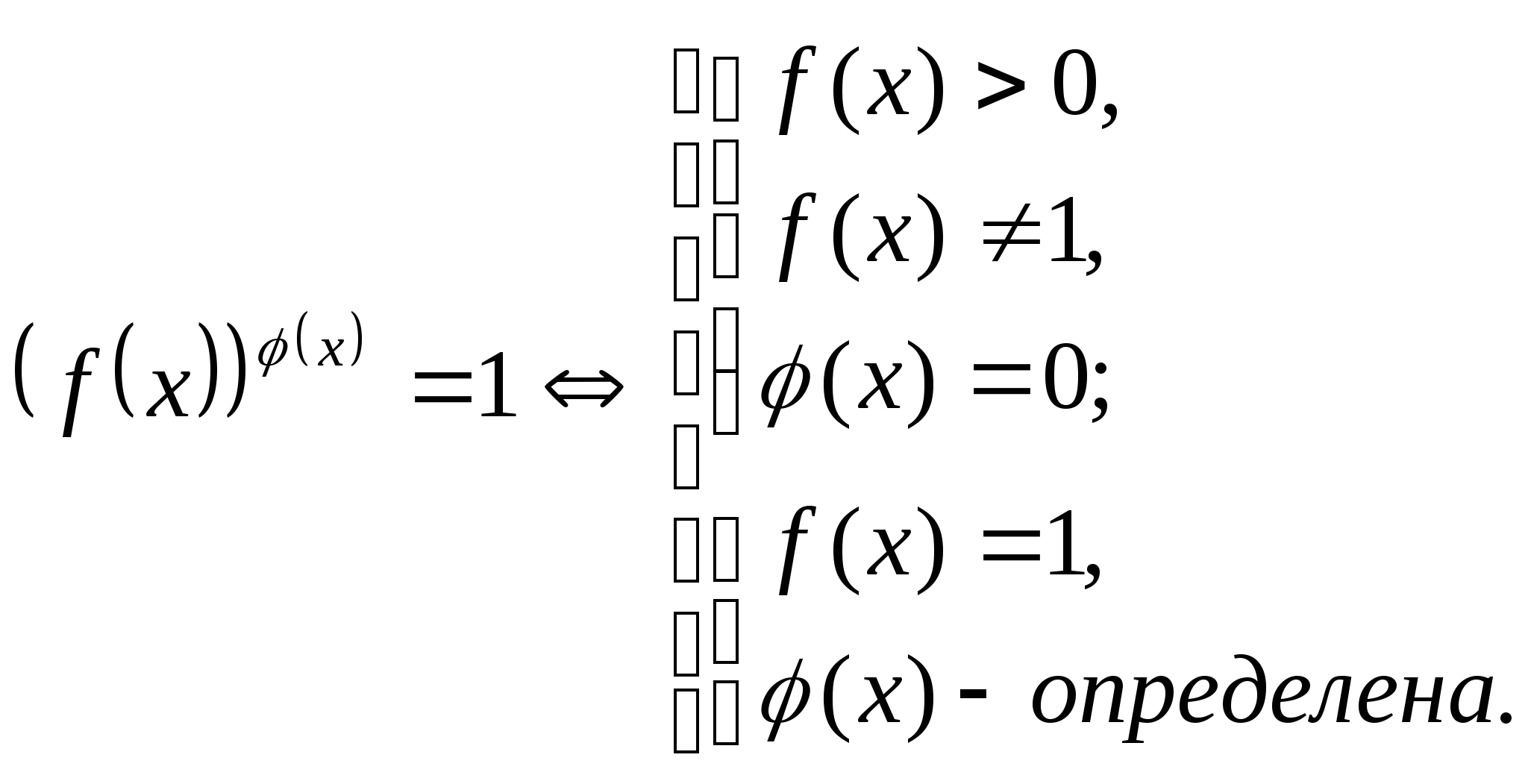
2. Уравнения вида :

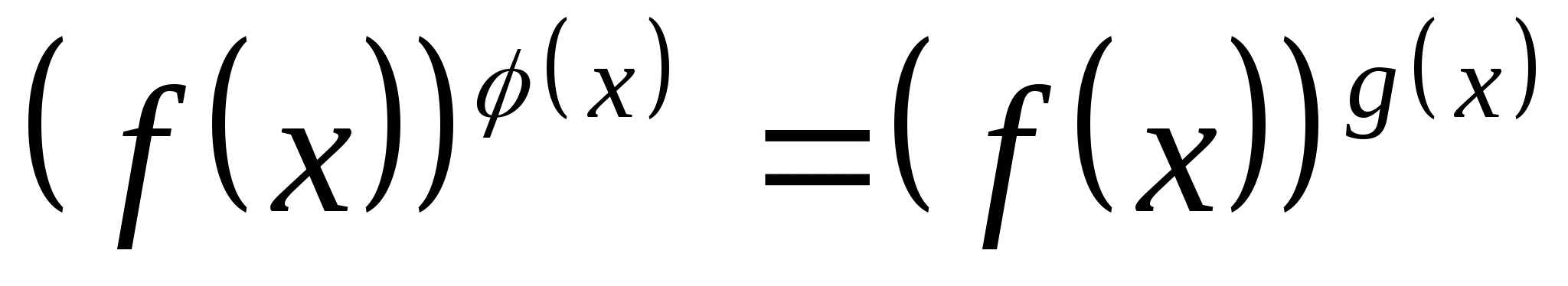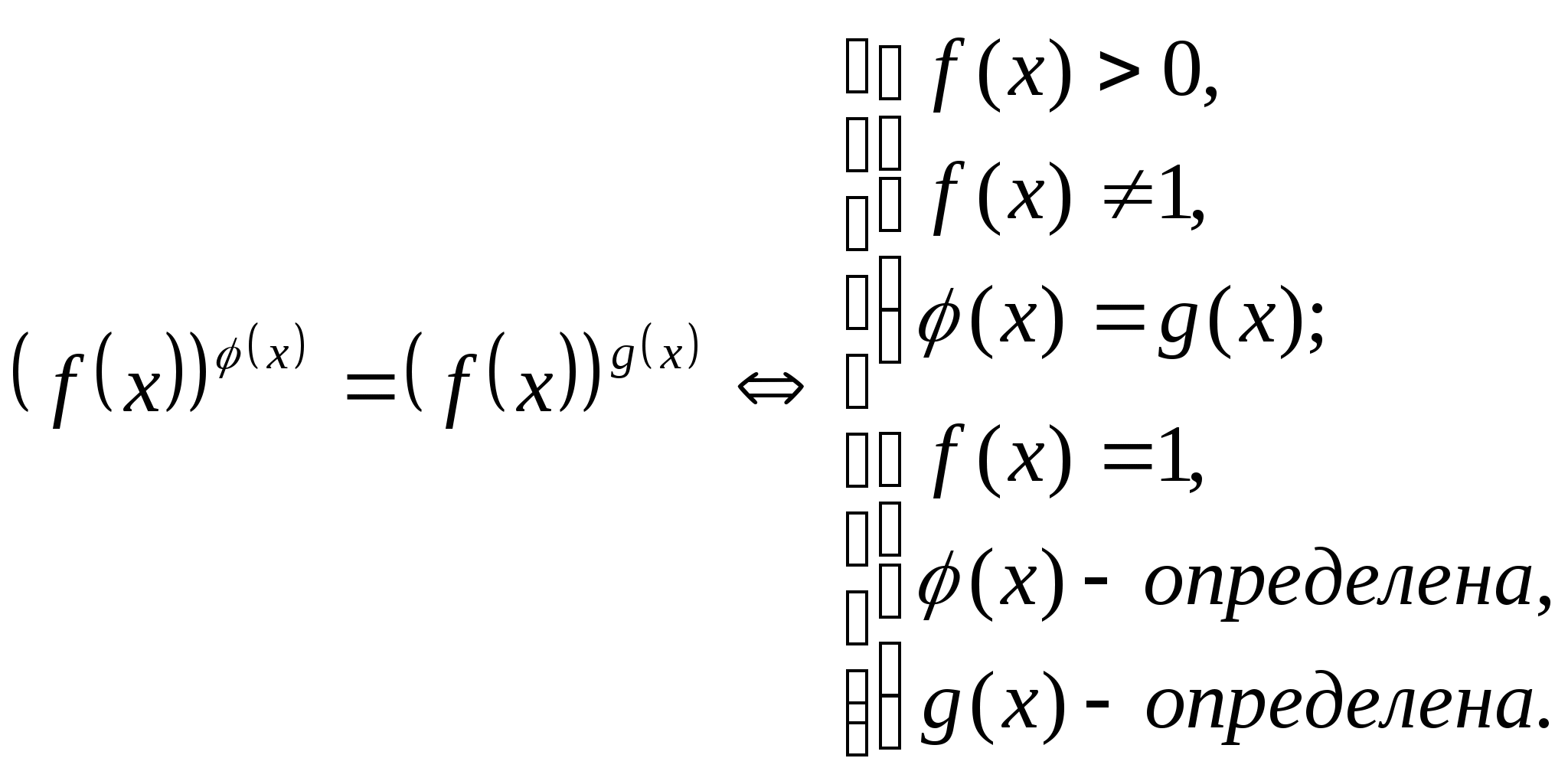
Данные уравнения можно также решать с помощью логарифмирования обеих частей уравнения по одному и тому же основанию и последующим разложением на множители: