Дидактический материал по математике для 10 класса

Тема «Основные свойства функций» вариант 1

1. Найти область определения функции
   
   а) [4;+∞) б) [-4; 4] в) (-∞; - 4]U[4; +∞) г) (-∞; 4]

2. Найти область значений функции у= - х² +5х - 9
   
   а) [;+∞) б) (-∞;-] в) (-∞; ] г) [;+∞)

3. Что можно сказать о функции
   
   а) четная б) нечетная в) ни четная, ни нечетная г) периодическая

4. Указать график функции
   
   а) б) в) г)
   
   
   
   
   
   
   
   
   
   
   
   

5. Дана функция f(x)=х³ - 2ах+5. Известно, что f(-1)=-3. Найти f(-2).
   
   а) 10 б) - 12 в) - 17 г) - 5

6. Найти область значений функции у=2 - 3sinx
   
   а) [-1; 5] б) [- 4; 2] в) [- 5; 1] г) [- 2; 4]

7. Найти нули функции
   
   а) 0 и √8 б) -4 и 4 в) √8 г) -2√2 и 2√2

8. Найти область определения функции у = 1/sinx

9. Найти f(3), если f(x) = x² +3x -1

10. Найти наименьший положительный период функции у=3tg(2x+π)-1

11. Определить по графику функции у=f(x)
    
    а) область определения
    
    б) область значений
    
    в) наименьшее значение функции
    
    г) достроить график периодической функции
    
    д) достроить график четной функции
    
    е) достроить график нечетной функции

12. Построить график функции у = 3 - 2sin(х+π/2)

вариант 2

1. Найти область определения функции
   
   а) (-∞; 12] б) [-√12; √12] в) [0; 12] г) [-12; 0]

2. Найти область значений функции у= х² +3х - 1
   
   а) (-∞;1,25] б) [-1,5;+∞) в) (-∞;- 1,5] г) [-3,25;+∞)

3. Что можно сказать о функции
   
   а) четная б) нечетная в) ни четная, ни нечетная г) периодическая

4. Указать график функции
   
   а) б) в) г)
   
   
   
   
   
   
   
   
   
   
   
   

5. Дана функция f(x)= - х³ - 4ах - 3. Известно, что f(-2)=1. Найти f(-1).
   
   а) 2 б) - 8 в) - 4 г) - 2

6. Найти область значений функции у=3 - 5сosx
   
   а) [-2; 2] б) [- 3; 5] в) [- 5; 3] г) [- 2; 8]

7. Найти нули функции
   
   а) √6 б) 2,45 в) 0 и √6 г) -√6 и √6

8. Найти область определения функции у = 1/соsx

9. Найти f(3), если f(x) = - x² +5x - 9

10. Найти наименьший положительный период функции у=2сtg(4x−π/2)+1

11. Определить по графику функции у=f(x)
    
    а) область определения
    
    б) область значений
    
    в) наибольшее значение функции
    
    г) достроить график периодической функции
    
    д) достроить график четной функции
    
    е) достроить график нечетной функции

12. Построить график функции у = - 2cos(х−π/2) - 2

Тема «Четные и нечетные функции»

ЗАЧЕТ «Функции и их свойства»

1. Понятийный диктант

1. Функция

2. Область значений функции

3. Убывающая функция

4. Четная функция и ее график

5. Экстремум

6. Минимум функции и точка минимума

2. Примеры

1. Приведите пример функции, если область определения функции:
   
   а) все действительные числа; б) все действительные числа, кроме 2,5.
   
   
   
   
   
   

2. Приведите пример функции, не имеющей нули.
   
   
   
   
   
   

3. Приведите пример графика функции у = g(х), если:

- область определения функции [-3; 2]

- область значений функции [-2; 4]

- на [-3; - 1] g(x) убывает, а на [- 1; 2] g(x) возрастает

- g(-3) = 1.

3. Математический диктант

Дана функция у = cosx. Укажите:

1. Область определения функции …

2. Область значений функции …

3. Данная функция четная или нечетная …

4. Данная функция имеет период …

5. График этой функции на промежутке пересекает ось Ох в точках х = …

6. График этой функции на промежутке пересекает ось Оу в точках у = …

7. На промежутке функция имеет максимум у = … при х = …

8. На промежутке функция имеет минимум у = … при х = …

9. В промежутке [-2π;2 π] функция монотонно убывает на участке …

10. В промежутке [-2π;2 π] функция монотонно возрастает на участке …

11. Выражение теряет смысл при следующих значениях х = …

. Тема «Преобразование тригонометрических выражений»1) 3cosα - sinα ctgα

2) 5 - sin²α - cos²α

3) (1 - sin²α)(1+tg²α)

1)

2) sin⁴α - cos⁴α + cos²α

3)

1)

2)

3)

№ 2. Докажите тождество:

1) cosα + cs(-α) = 0

2)

1)

2)

1) sin⁴α - sin²α + cos²α = cos⁴α

2) 1 - sin²α cos²α - cos⁴α =

= 1 - sinα cosα ctgα

№ 3. Найдите значение выражения:

1+ cos² α - sin² α,

cosα = 0,8

, ctgα = 0,125

(sinα + cosα)² - 2sinα(cosα - sinα),

sinα = 0,7

№ 4. Найти наибольшее и наименьшее значение выражения:

5sin²α + 3cos²α

Дополнительно. № 5. Докажите тождество:

Тема «Свойства синуса, косинуса, тангенса, котангенса»

1. Углом какой четверти является угол
   
   а) 98^о; - 282^о; -98^о; 282^о; 369^о; - 369^о; 480^о; -930^о; 2000^о
   
   б) sin a > 0 и tg a < 0 ?

2. Имеет ли смысл выражение
   
   а) tg270^o б) sin270^o в) cosa = √5/2 г) ctg a = √5/2 д)

3. Укажите наибольшее и наименьшее значение функции 4 - sin a.

4. Вычислите:
   
   а) 6tg180^o + 3ctg90^o г) sin²60^o + cos²30^o
   
   б) sin270^o - 2cos180^o д) ctg750^o · sin(-60^o) · tg(-30^o)
   
   в)√2sin45^o + √2cos45^o е) cos(-180^o) · sin(- 30^o)

5. Сравните:

6. Найдите значение выражения:
   
   а) sin3a, если a=30^o б)

Тема «Параллельность прямых и плоскостей»

1. Трапеция АВСД с основаниями АД и ВС и прямоугольник АМКД не лежат в одной плоскости. Точки О и Н - середины отрезков АВ и СД соответственно.
   
   а) Докажите, что ОН и МК параллельны
   
   б) Найдите ОН, если ВС = 8см и МК = 12см

2. Точки А, В, С, Д не лежат в одной плоскости. Среди прямых, проходящих через любые две из данных точек, укажите прямую, которая является скрещивающейся: а) с прямой АВ; б) с прямой ВС. (ответ обоснуйте)

3. Дан куб АВСДА₁В₁С₁Д₁. Укажите три прямые, проходящие:
   
   а) через точку Д и скрещивающиеся с прямой АВ₁
   
   б) через точку В₁ и скрещивающиеся с прямой А₁Д

4. Ответить на вопросы:
   
   1) верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?
   
   2)две прямые параллельны некоторой плоскости. Могут ли эти прямые а) пересекаться; б) быть скрещивающимися?
   
   3) могут ли скрещивающиеся прямые а и b быть параллельными прямой с?
   
   4)даны две скрещивающиеся прямые а и b. точки А и А₁ лежат на прямой а, точки В и В₁ лежат на прямой b. как будут расположены прямые АВ и А₁В₁?
   
   5) прямая а скрещивается с прямой b , а прямая b скрещивается с прямой с. Следует ли из этого, что прямые а и с - скрещиваются?
   
   6) каково должно быть взаимное расположение трех прямых, чтобы можно провести плоскость, содержащую все прямые?

5. Дан куб АВСДА₁В₁С₁Д₁. Найдите угол между прямыми 1) ВС и СС₁ 2) АС и ВС 3) Д₁С₁ и ВС 4) А₁В₁ и АС.

6. Треугольники АВС и АДС лежат в разных плоскостях. РК - средняя линия треугольника АДС с основанием АС. Определить взаимное расположение прямых РК и АВ и найти угол между ними, если угол С равен 80^о и угол В равен 40^о.

7. Трапеция АВСД (АД и ВС - основания) и треугольник АЕД лежат в разных плоскостях. МР - средняя линия треугольника АЕД (МР параллельно АД). Каково взаимное расположение прямых МР и АВ? Чему равен угол между этими прямыми, если угол АВС равен 110^о?

Тема «Построение сечений тетраэдра и параллелепипеда»

1. Построить сечение тетраэдра ДАВС плоскостью, проходящей через данные точки М, О, К. М€ДВ, О€ДС, К€ДА,

2. Построить сечение тетраэдра ДАВС плоскостью, проходящей через данные точки М, О, К - середины ребер АВ, ВС, ДС. Найти периметр сечения. Ребро тетраэдра равно а.

3. Построить сечение тетраэдра ДАВС плоскостью, проходящей через данные точки М, О, К. М€АВ, О€ВС, К€СД, ОМ ║АС.

4. Построить сечение тетраэдра ДАВС плоскостью, проходящей через данные точки М, О, К. М€ДВ, О€ДС, К€САВ.

5. Построить сечение тетраэдра ДАВС плоскостью, проходящей через точку М€ДАВ, параллельно плоскости СВД.

6. Построить сечение тетраэдра ДАВС плоскостью, проходящей через данные точки М, Е, К. М€ДВ, Е€ДС, К€СА.

7. Построить сечение куба ДАВСД₁А₁В₁С₁ плоскостью, проходящей через данные точки, являющиеся серединами трех соседних ребер. Найти периметр сечения, если ребро куба равно а.

8. Построить сечение куба ДАВСД₁А₁В₁С₁ плоскостью, проходящей через данные точки А, С, Н, если Н€ДД₁.

9. Построить сечение куба ДАВСД₁А₁В₁С₁ плоскостью, проходящей через данные точки А, Д₁, Н, Е, если Н середина СС₁, Е середина ВС.

10. Построить сечение параллелепипеда ДАВСД₁А₁В₁С₁ плоскостью, проходящей через данные точки Н, Е, Р, если Н€А₁Д₁, Е€АВ, Р€ВС.

11. Все грани параллелепипеда ДАВСД₁А₁В₁С₁ - равные ромбы со стороной а и острым углом 60^о. Построить сечение параллелепипеда плоскостью, проходящей через точки Д, В, М, если М середина ВС. Доказать, что построенное сечение есть равнобедренная трапеция. Найти стороны трапеции.

Тема «Перпендикулярность прямой и плоскости»

1.

Доказать, что прямая АС перпендикулярна плоскости АМВ.

M

A B

C

2.

МВDС - прямоугольник. Доказать, что прямая СD перпендикулярна плоскости АВС.

M

D

B

A

C

3.

АВСD - прямоугольник. Доказать, что АD перпендикулярна АМ.

M

B C

A D

4.

Доказать, что ВС перпендикулярна ЕD.

M

E

A B

D

C

5.

АВСD - параллелограмм. Доказать, что прямая МО перпендикулярна плоскости АВС.

M

B C

O

A D

6.

АВСD - ромб. Доказать, что ВD перпендикулярна плоскости АМС.

M

B C

O

A D

Тема «Перпендикулярность прямой и плоскости»

1. Закончите предложение, чтобы получилось верное утверждение.

Сделайте чертеж.

1. Две прямые называются перпендикулярными, если …

2. Если плоскость перпендикулярна одной из двух параллельных прямых, то она …

3. Если две плоскости перпендикулярны прямой, то они …

4. Прямая называется перпендикулярной к плоскости, если …

5. Две прямые, перпендикулярные одной и той же плоскости …

6. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая …
   
   
   
   

2. Ответьте на вопрос.

Сколько перпендикуляров можно провести через данную точку к данной прямой в пространстве?

3. Выпишите (см.рис.) B₁ C₁

1. ребра, перпендикулярные плоскости DСС₁

2. плоскости, перпендикулярные ребру ВВ₁ A₁ D₁

4. Используя символы ┴ и ║, запишите,

как расположены прямая и плоскость B C

(см.рис.). Докажите.

1. СС₁ и DСВ

2. D₁С₁ и DСВ A D

5. Обоснуйте ответ.

Каково взаимное расположение прямой АС и плоскости α, если АВ ┴ α,

СD ┴ α, B α, Dα, AB = CD.

Тема «Производная» (100 минут)

Закрытые задания (по 3 балла):

1. Найти производную у = х⁹ + 3х⁷ +6

   1. 9х⁸ + 21х⁶ +6 b) 9х + 21х⁶ + 6 с) 9х⁸ + 21х⁶ + 6х d)9х⁸ + 21х⁶

2. Найти f ' (1), если f(x) = (2x - 3) / (5 - 4x)

   1. - 2 b) 1/4 c) 6

3. Указать, для какой из функций f(x) = 9x² + cosx, g(x) = 4,5x² - sinx, h(x) = 18x + sinx, функция
   
   y=9x - cosx является производной.

   1. f(x) b) g(x) c) h(x)

4. Найти критические точки для f(x) = 3x⁴ - 2x³

   1. 0 и -1/2 b) 0 и 1/2 с) 0 и 2/3

5. Найти наименьшее значение функции у = х³ - 3х на отрезке [0; 2]

   1. -4 b) -2 c) 0 d) 2

6. Вычислить скорость материальной точки, движущейся по закону s = 2t² - 8t + 11 в момент времени
   
   t₀ = 2с, s - путь в метрах, t - время в секундах

   1. 0 м/с b) 3 м/с c) 11 м/с

7. Указать промежутки убывания функции, если график ее производной имеет следующий вид
   
   у
   
   3
   
   
   
   
   
   -3 2 4 х
   
   
   
   

   1. [-3; 2] b) [0; 3] c) [2; 4]

8. Определить абсциссу точки, для которой угловой коэффициент к графику функции g(x) = √x - x, равен 1

   1. -1/2 b) 1/16 c) 1/2 d) 1 e) 16

9. Найти точки максимума функции f(x) = x + 4/x

   1. -2 b) -1/4 c) ±2 d) 0 e) 2

10. На каком из данных рисунков изображен график функции, для которой х = - 3 точка максимума, х=4 точка минимума у
    
    1) у 2) у 3) у 4)
    
    
    
    х х х х
    
    -3 4 -3 4 -3 4 -3 4
    
    
    
    

    1. 1 b) 2 c) 3 d) 4

11. Найти производную функции у = xsinx

    1. - cosx b) cosx c) sinx - xcosx d) sinx +xcosx

12. Найти производную функции у = tg²2x

    1. - 4tg2x / sin²x b) 2tg2x c) 4tg2x / cos²2x d) 4tg2x

Открытые задания:

13. Найти производную функции у = (х² - 1)(х² +1) (3б)

14. Написать уравнение касательной к уравнению функции f(x) = x³ + 2x² - 1 в точке x₀ = -1 (6б)

15. Доказать, что функция f(x) = (x³ - 3)⁵ возрастает на всей области определения (5б)

16. Исследуйте функцию и постройте ее график у = х⁴ - 2х³ + 3 (8б)

17. Представьте число 12 в виде суммы двух положительных слагаемых так, чтобы сумма их квадратов была наименьшей (7б)

18. Найти производную функции (5б)

Контрольная работа по математике в 10 классе за 1 полугодие

1. </ Вычислить
   
   
   
   

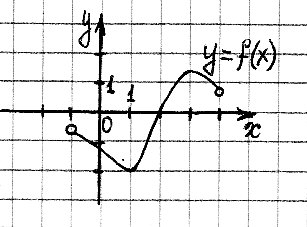
2. Найти длину промежутка возрастания функции,
   
   график которого изображен на рисунке.
   
   
   
   

3. Найти сумму наибольшего и наименьшего значений функции .

4. Можно ли провести через середину медианы треугольника прямую, которая не имеет общих точек с его сторонами? Ответ поясните.

5. Вычислить

6. Сколько целых чисел входит в область определения функции .

7. Упростить выражение .

8. Найти площадь равностороннего треугольника, сторона которого равна .
   
   
   
   

9. На одном из рисунков изображен график четной функции. Указать этот рисунок.
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   

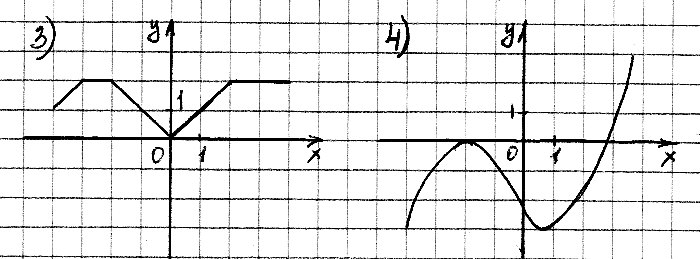
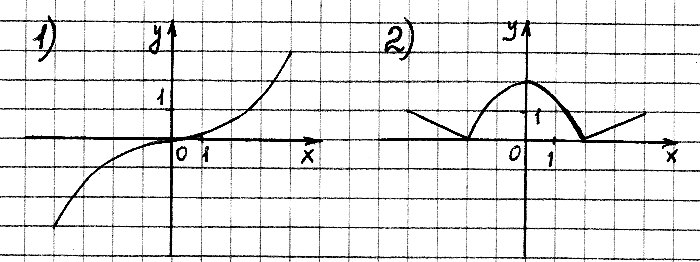
10. Найти значение , где Т_о - наименьший положительный период функции f(x)=4sin2x.

11. Вычислить .

12. Ребро куба равно . Найти площадь полной поверхности куба.

13. Функция у=f(x) определена на всей числовой прямой и является нечетной. На промежутке (0; 6) она задается формулой f(x)=6x - x². Найти f(- 2).
    
    
    
    

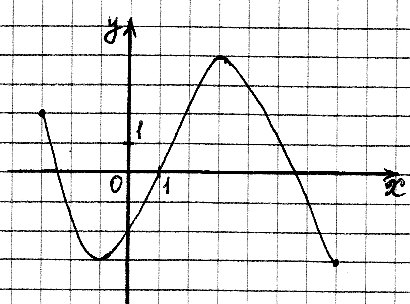
14. На рисунке изображен график функции у=f(x).
    
    Найти: а) точку максимума; б) минимум функции.
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    

15. Через точку D, лежащую между параллельными плоскостями α и β, проведены прямые m и k. Прямая m пересекает плоскости α и β в точках М₁ и М₂ соответственно, а прямая k - в точках К₁ и К₂ соответственно. Вычислите длину отрезка DМ₂, если М₁М₂=20дм,
    
    М₁К₁ : М₂К₂ = 3 : 7.