МБОУ «Лицей» г.Протвино Московской области

Исследовательская работа на тему

«Теорема Пифагора»

Выполнена ученицей

9 класса МБОУ «Лицей»

Калининой Алиной Андреевной

Научный руководитель -

учитель МБОУ «Лицей»

Довлатбегян

Виктория Александровна

Протвино 2015

Содержание:

Цели и задачи проекта…………………………………………………………….3

Глава 1. История Пифагора и теоремы Пифагора………………………………..4

1.1.Что такое теорема Пифагора и биография Пифагора………………………4

1.1.1.Не много о Пифагоре……………………………………………………….4

1.1.2.Биография Пифагора………………………………………………………..4

1.2. История теоремы Пифагора…………………………………………………5

Глава 2.Формулировки теоремы Пифагора………………………………………….6

2.1.Геометрическая формулировка………………………………………………6

2.2.Алгебраическая формулировка………………………………………………6

2.3.Обратная формулировка теорема Пифагора………………………………...6

Глава 3.Доказательство теоремы Пифагора………………………………………7

3.1.Не много о доказательствах………………………………………………….7

3.2.Доказательство через подобные треугольники……………………………..7

3.3.Доказательства методом площадей………………………………………….8

3.3.1..Доказательство через равнодополняемость………………………………8

3.3.2.Доказательство Евклида……………………………………………………9

3.3.3.Доказательство Леонардо да Винчи……………………………………...11

3.4.Доказательство методом бесконечно малых………………………………12

Глава4.Вариации и обобщения………………………………………………………...14

4.1.Подобные геометрические фигуры на трех сторонах…………………….14

4.2.Теорема косинусов…………………………………………………………..15

Глава 5.Теория чисел…………………………………………………………………….16

Результаты и Источники………………………………………………………...17

Цели и задачи проекта

1. Изучить теорему Пифагора и изучить историю теоремы

2. Доказать теорему Пифагору

Глава 1. История Пифагора и теоремы Пифагора.

1.1.Что такое теорема Пифагора и биография Пифагора.

Теорема Пифагора - одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

1.1.1.Немного о Пифагоре

Пифагор Самосский (др.-греч. Πυθαγόρας ὁ Σάμιος, лат. Pythagoras; 570-490 гг. до н. э.) - древнегреческий философ, математик и мистик, создатель религиозно-философской школы пифагорейцев.

1.1.2.Биография Пифагора

Основными источниками по жизни и учению Пифагора являются сочинения философа-неоплатоника Ямвлиха (242-306 гг.) «О Пифагоровой жизни»; Порфирия(234-305 гг.) «Жизнь Пифагора»; Диогена Лаэртского (200-250 гг.) кн. 8, «Пифагор». Эти авторы опирались на сочинения более ранних авторов, из которых следует отметить ученика Аристотеля Аристоксена (370-300 гг. до н. э.) родом из Тарента, где сильны были позиции пифагорейцев. Таким образом, самые ранние известные источники об учении Пифагора появились лишь 200 лет спустя после его смерти. Сам Пифагор не оставил сочинений, и все сведения о нём и его учении основываются на трудах его последователей, не всегда беспристрастных.

Родителями Пифагора были Мнесарх и Партенида с острова Самос. Мнесарх был камнерезом (Диоген Лаэртский); по словам же Порфирия он был богатым купцом из Тира, получившим самосское гражданство за раздачу хлеба в неурожайный год. Первая версия предпочтительнее, так как Павсаний приводит генеалогию Пифагора по мужской линии от Гиппаса из пелопоннесского Флиунта, бежавшего на Самос и ставшего прадедом Пифагора. Партенида, позднее переименованная мужем в Пифаиду, происходила из знатного рода Анкея, основателя греческой колонии на Самосе.

1.2. История теоремы Пифагора

Ещё известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммурапи, то есть к 2000 году до н. э., приводится приближённое вычисление гипотенузы равнобедренного прямоугольного треугольника]. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях.

Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой - на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал вывод о большой вероятности того, что теорема о квадрате гипотенузы была известна в Вавилоне уже около XVIII века до н. э.

Согласно комментарию Прокла к Евклиду, Пифагор (годами жизни которого принято считать 570-490 гг. до н. э.) использовал алгебраические методы, чтобы находить пифагоровы тройки. Однако Прокл писал между 410 и 485 гг. н. э. Томас Литтл Хит (en:Thomas Little Heath) считал, что не существует явного упоминания, относящегося к периоду продолжительностью 5 веков после смерти Пифагора, что Пифагор был автором теоремы.] Однако, когда авторы, такие как Плутарх и Цицерон, пишут о теореме Пифагора, они пишут так, как будто авторство Пифагора было широко известным и несомненным. «Принадлежит ли эта формула лично перу Пифагора…, но мы можем уверенно считать, что она принадлежит древнейшему периоду пифагорейской математики». По преданию, Пифагор отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков.

Приблизительно в 300 г. до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора.

Глава 2.Формулировки теоремы Пифагора.

2.1.Геометрическая формулировка:

Изначально теорема была сформулирована следующим образом:

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

2.2.Алгебраическая формулировка:

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

То есть, обозначив длину гипотенузы треугольника через, а длины катетов через и :

Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.

2.3.Обратная формулировка теорема Пифагора:

Для всякой тройки положительных чисел 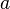, 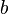и , такой, что 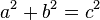, существует прямоугольный треугольник с катетам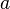и и 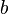и гипотенузой .

Глава 3.Доказательство теоремы Пифагора

3.1.Не много о доказательствах

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.

Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений).

В моём проекте приведено пять примеров доказательств данной теоремы:

1. Через подобные треугольники

2. Методом площадей

2.1. Через равнодополняемость

2.2. Доказательство Евклида

3. Методом бесконечно малых

3.2.Доказательство через подобные треугольники

Следующее доказательство алгебраической формулировки - наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.

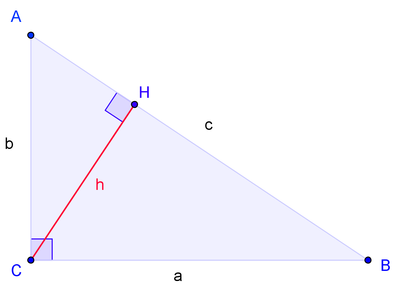
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения

получаем

Что эквивалентно

Сложив, получаем

или

, что и требовалось доказать

3.3.Доказательства методом площадей

Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

3.3.1..Доказательство через равнодополняемость

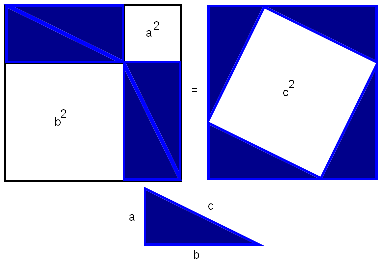
Рис.1

1. Расположим четыре равных прямоугольных треугольника так, как показано на рисунке 1.

2. Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол - 180°.

3. Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата.

Что и требовалось доказать.

3.3.2.Доказательство Евклида

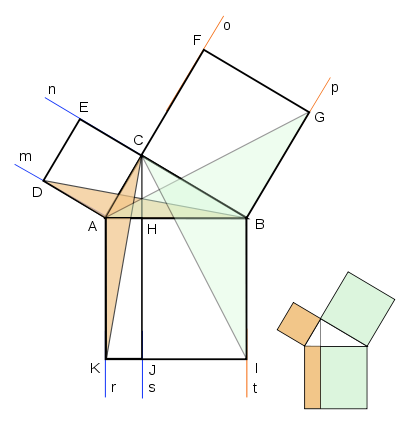
Чертеж к доказательству Евклида

Иллюстрация к доказательству Евклида

Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны.

Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника - BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах.

Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK. Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.

Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, - это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно: треугольники равны по двум сторонам и углу между ними. Именно - AB=AK, AD=AC - равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата - 90°).

Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично.

Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах. Идея данного доказательства дополнительно проиллюстрирована с помощью анимации, расположенной выше.

Данное доказательство также получило название «Пифагоровы штаны».

3.3.3.Доказательство Леонардо да Винчи

Доказательство Леонардо да Винчи

Главные элементы доказательства - симметрия и движение.

Рассмотрим чертёж, как видно из симметрии, отрезок рассекает квадрат на две одинаковые части (так как треугольники и равны по построению).

Пользуясь поворотом на 90 градусов против часовой стрелки вокруг точки , мы усматриваем равенство заштрихованных фигур и .

Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей маленьких квадратов (построенных на катетах) и площади исходного треугольника. С другой стороны, она равна половине площади большого квадрата (построенного на гипотенузе) плюс площадь исходного треугольника. Таким образом, половина суммы площадей маленьких квадратов равна половине площади большого квадрата, а следовательно сумма площадей квадратов, построенных на катетах равна площади квадрата, построенного на гипотенузе.

3.4.Доказательство методом бесконечно малых

Следующее доказательство при помощи дифференциальных уравнений часто приписывают известному английскому математику Харди, жившему в первой половине XX века.

Рассматривая чертёж, показанный на рисунке, и наблюдая изменение стороны a, мы можем записать следующее соотношение для бесконечно малых приращений сторон с и a (используя подобие треугольников):

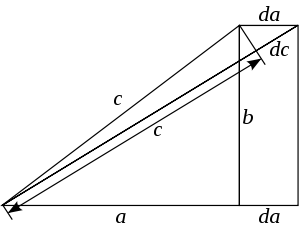
Доказательство методом бесконечно малых

Пользуясь методом разделения переменных, находим

Более общее выражение для изменения гипотенузы в случае приращений обоих катетов

Интегрируя данное уравнение и используя начальные условия, получаем

Таким образом, мы приходим к желаемому ответу

Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.

Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения (в данном случае катет ). Тогда для константы интегрирования получим

Глава 4 Вариации и обобщения

4.1.Подобные геометрические фигуры на трех сторонах

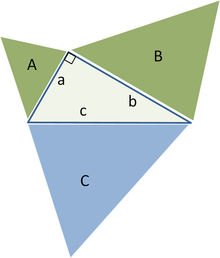
Обобщение для подобных треугольников, площадь зеленых фигурA + B = площади синей C

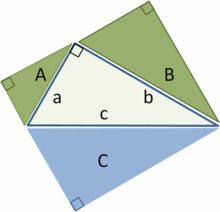
Теорема Пифагора с использованием подобных прямоугольных треугольников

Обобщение теоремы Пифагора сделал Евклид в своей работе Начала, расширив площади квадратов на сторонах до площадей подобных геометрических фигур:

Если построить подобные геометрические фигуры на сторонах прямоугольного треугольника, тогда сумма двух меньших фигур будет равняться площади большей фигуры.

Главная идея этого обобщения заключается в том, что площадь подобной геометрической фигуры пропорциональна квадрату любого своего линейного размера и в частности квадрату длины любой стороны. Следовательно, для подобных фигур с площадями A, B и C построенных на сторонах с длиной a, b и c, имеем:

Но, по теореме Пифагора, a² + b² = c², тогда A + B = C.

И наоборот, если мы сможем доказать, что A + B = C для трех подобных геометрических фигур без использования теоремы Пифагора, тогда мы сможем доказать саму теорему, двигаясь в обратном направлении. Например, стартовый центральный треугольник может быть повторно использован как треугольник C на гипотенузе, и два подобных прямоугольных треугольника (A и B), построенные на двух других сторонах, которые образуются в результате деления центрального треугольника его высотой. Сумма двух меньших площадей треугольников тогда, очевидно, равна площади третьего, таким образом A + B = C и, выполняя предыдущее доказывания в обратном порядке, получим теорему Пифагора a² + b² = c².

4.2.Теорема косинусов

Теорема Пифагора - это частный случай более общей теоремы косинусов, которая связывает длины сторон в произвольном треугольнике:

где θ - угол между сторонами a и b.

Если θ равен 90 градусов, тогда cosθ = 0 и формула упрощается до обычной теоремы Пифагора.

Глава 5.Теория чисел

Пифагоровой тройкой называется набор из трёх натуральных чисел удовлетворяющих следующему однородному квадратному уравнению</:

Формулировка «Великой теоремы Ферма» аналогична задаче нахождения пифагоровых троек для степени более 2.

Результаты

Все цели и задачи выполнены

Источники

www.matematika.ru

ru.wikipedia.org