Методические указания по теме Арифметический квадратный корень

Корни п-ой степени.

Арифметический квадратный корень

Уравнение имеет два решения: x=2 и x=-2. Это числа, квадрат которых равен 4.

Рассмотрим уравнение . Нарисуем график функции и увидим, что и у этого уравнения два решения, одно положительное, другое отрицательное.

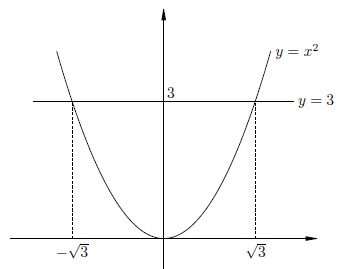
Но в данному случае решения не являются целыми числами. Более того, они не являются рациональными. Для того, чтобы записать эти иррациональные решения, мы вводим специальный символ квадратного корня.

Арифметический квадратный корень - это неотрицательное число, квадрат которого равен , a ≥ 0. При a < 0 - выражение не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу .

Корень из квадрата

Например, . А решения уравнения соответственно и

Кубический корень

Кубический корень из числа - это число, куб которого равен . Кубический корень определен для всех . Его можно извлечь из любого числа: .

Корень n-ой степени

Корень -й степени из числа - это число, -я степень которого равна .

Если - чётно.

• Тогда, если a < 0 корень n-ой степени из a не определен.

• Или если a ≥ 0, то неотрицательный корень уравнения 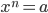называется арифметическим корнем n-ой степени из aи обозначается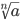

Если - нечётно.

• Тогда уравнение 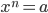имеет единственный корень при любом .

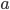Пример 4.

</ Таблица корней

Корень седьмой степени (7)

Корень четвертой степени (4)

Корень восьмой степени (8)

Корень пятой степени (5)

Корень девятой степени (9)

Корень шестой степени (6)

Корень десятой степени (10)