Пробный экзамен (проф. уровень).Пять вариантов с ответами

Вариант №5

1. Магазин закупает цветочные горшки по оптовой цене рублей за штуку. Торговая наценка составляет 15%. Какое наибольшее число таких горшков можно купить в этом магазине на рублей?

2. Посев семян тыквы рекомендуется проводить в мае при дневной температуре воздуха не менее ° С. На рисунке показан прогноз дневной температуры воздуха в первой и второй декадах мая. Определите, в течение скольких дней за этот период можно производить посев тыквы.

3. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

4. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно три раза.

5. Найдите корень уравнения

6. В треугольнике угол Cравен 90⁰, sinA=, AC = 6. НайдитеAB.

7. Прямая является касательной к графику функции у = х³ -3х² + 4х + 8 . Найдите абсциссу точки касания.

8. Найдите обьем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Часть 2

9. Найдите значение выражения .

10. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур даётся выражением , где К, К/мин, К/(мин). Известно, что при температурах нагревателя свыше 500 К прибор может испортиться, поэтому его нужно отключать. Определите (в минутах) через какое наибольшее время после начала работы нужно отключать прибор.

11. Два велосипедиста одновременно отправляются в 154 -километровый пробег. Первый едет со скоростью на 3 км/ч большей, чем второй и прибывает к финишу на 3 ч раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.

12. Найдите наименьшее значение функции на отрезке .

13. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

14. В треугольной пирамиде MABC с основанием ABC ребро MA перпендикулярно плоскости основания, стороны основания равны 3, а ребро MB равно 5. На ребре AC находится точка D, на ребре AB точка E, а на ребре AM - точка L. Известно, что AD = 2 и BE = ML = 1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D и L.

15. Решите неравенство

16. В остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и

17. По вкладу «А» банк в конце каждого года планирует увеличивать на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» - увеличивать эту сумму на 10% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.

18. Найдите все такие значения параметра a, при каждом из которых уравнение не имеет решений.

19. Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и все их возможные суммы (по 2, по 3 и т.д.) выписывают на доске в порядке неубывания. Если какое-то число n, выписанное на доске, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.

а) Приведите пример задуманных чисел, для которых на доске будет записан набор 3, 6, 9, 12, 15.

б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 5, 6, 8, 9, 11, 12, 13, 14, 17, 18, 19, 21, 23?

в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 8, 9, 10, 17, 18, 19, 20, 27, 28, 29, 30, 37, 38, 39, 47.

Вариант №4

1. Больному прописано лекарство, которое нужно пить по г 3раза в день в течение дня. Лекарство выпускается в упаковках по 8 таблеток по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?

2. На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций горнодобывающей компании в первой половине сентября. 7 сентября бизнесмен купил пакет акций, а 13 сентября продал его. В результате этих операций прибыль бизнесмена составила 3600 рублей. Сколько акций было в пакете?

3. На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.

4. В среднем из 50 поступивших в продажу аккумуляторов48 аккумуляторов заряжены. Найдите вероятность того, чтокупленный аккумулятор не заряжен.

5. Найдите корень уравнения .

6. В треугольнике угол Cравен 90⁰, AB = 35, cosB =. Найдите AC.

7. На рисунке изображен график производной функции , определенной на интервале(-6;6). Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.

8. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 14.

Часть 2

9. Найдите значение выражения

10. Для определения эффективной температуры звёзд используют закон Стефана - Больцмана, согласно которому мощность излучения нагретого тела вычисляется по формуле: , где , площадь S поверхности измеряется в квадратных метрах, температура T - в градусах Кельвина, а мощность - в ваттах. Известно, что некоторая звезда имеет площадь , а излучаемая ею мощность P не менее Вт. Определите наименьшую возможную температуру этой звезды (в градусах Кельвина).

11. Первый рабочий за час делает на 3 детали больше, чем второй рабочий, и заканчивает работу над заказом, состоящим из 567 деталей, на 6 часов раньше, чем второй рабочий выполняет заказ, состоящий из 648 таких же деталей. Сколько деталей делает в час первый рабочий?

12. Найдите наибольшее значение функции на отрезке .

13. Решите уравнение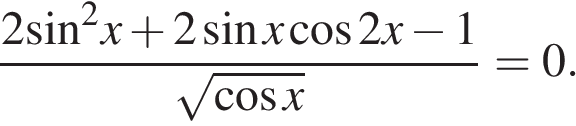

14. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны ребра:AB = 6, AD = 8, CC₁ = 16. Найдите угол между плоскостями ABC и A₁DB.

15. Решите неравенство:

16. Около равнобедренного треугольника ABC с основанием BC описана окружность. Через точку C провели прямую, параллельную стороне AB. Касательная к окружности, проведённая в точке B, пересекает эту прямую в точке K.

а) Докажите, что треугольник BCK - равнобедренный.

б) Найдите отношение площади треугольника ABC к площади треугольника BCK, если

17. 31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?

18. Найти все значения a, при каждом из которых система

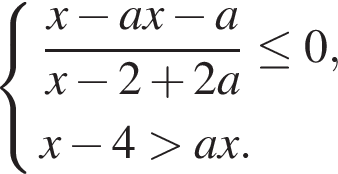
имеет решения.

19. Последние члены двух конечных арифметических прогрессий a₁ = 5, a₂= 8, ..., a_N и b₁ = 9, b₂ = 14, ..., b_M совпадают, а сумма всех совпадающих (взятых по одному разу) членов этих прогрессий равна 815. Найдите число членов в каждой прогрессии.

Вариант №3

1. Железнодорожный билет для взрослого стоит рублей. Стоимость билета школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 14школьников и 3взрослых. Сколько рублей стоят билеты на всю группу?

2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали - значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурой воздуха 19 декабря.

3. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

4. В некотором городе из 2000 появившихся на свет младенцев 990 девочек. Найдите частоту рождения мальчиков в этом городе. Ответ округлите до тысячных.

5. Найдите корень уравнения:

6. В параллелограмме ABCD . Найдите .

7. На рисунке изображен график производной функции , определенной на интервале(-9;8). В какой точке отрезка[-8;-4] принимает наименьшее значение.

8. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.

Часть 2

9. Найдите значение выражения .

10. Коэффициент полезного действия некоторого двигателя определяется формулой %. При каком наименьшем значении температуры нагревателя КПД этого двигателя будет не менее 40%, если температура холодильника ?

11. Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 1 час 40 минут, баржа отправилась назад и вернулась в пункт А в 21:00. Определите (в км/час) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.

12. Найдите точку максимума функции .

13. Решите уравнение .

14. Косинус угла между боковой гранью и основанием правильной треугольной пирамиды равен Найдите угол между боковыми гранями этой пирамиды.

15. Решите неравенство:

16. Радиус окружности, описанной около треугольника ABC, равен 13, высота, проведённая к стороне BC, равна 5. Найдите длину той хорды AM описанной окружности, которая делится пополам стороной BC.

17. Консервный завод выпускает фруктовые компоты в двух видах тары - стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.

Вид тары

Себестоимость,

1 ц.

Отпускная цена,

1 ц.

стеклянная

1500 руб.

2100 руб.

жестяная

1100 руб.

1750 руб.

Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью).

18. Найдите все значения a, при которых уравнение имеет хотя бы один корень, принадлежащий промежутку (−1; 1].

19. Натуральные числа a, b, c и d удовлетворяют условию a > b > c > d.

а) Найдите числа a, b, c и d, если a + b + с + d = 15 и a² − b² + с² − d² = 19.

б) Может ли быть a + b + с + d = 23 и a² − b² + с² − d² = 23?

в) Пусть a + b + с + d = 1200 и a² − b² + с² − d² = 1200. Найдите количество возможных значений числа a.

Вариант №2

1. Билет в музей стоит 270 рублей. Для группы от 10 человек делается скидка в размере 15 %. Сколько стоит групповой билет на 14 человек?

2. Диаграмма на рисунке представляет собой координатную плоскость, где по горизонтальной оси откладывается температура воздуха в градусах Цельсия, а по вертикальной оси - относительная влажность воздуха в процентах. Закрашенная фигура на диаграмме представляет собой область наиболее комфортного размножения плесневого грибка в помещении (при поддержании соответствующих условий непрерывно в течение суток). Определите, при какой максимальной относительной влажности плесень будет активно размножаться, если температура в помещении равна 20∘C.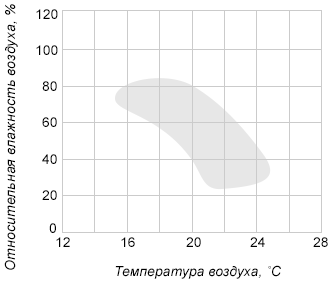

Ответ дайте в процентах.

3. Найдите площадь треугольника, вершины которого имеют координаты (1;6), (10;6), (2;8).

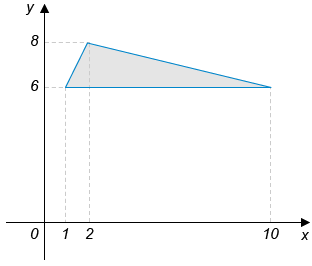
4. Учительница разбила класс на 8 групп по 4 человека, выдав каждой группе тему доклада для следующего урока и назначив старшего в группе. Антон - старший в некоторой группе - накануне весь вечер играл в футбол, поэтому его группа доклад не подготовила. Учительница может вызывать для презентации доклада любого учащегося, кроме старших по группам. Какова вероятность, что вызовут школьника из группы Антона?

5. Найдите корень уравнения log₃(x²−6x) = log₃(5−2x). В случае, если уравнение имеет несколько корней, в ответе запишите их сумму.

6. В ромбе ABCD из вершины тупого угла D к стороне BC проведен перпендикуляр DK. BK=4 см, KC=6 см. Вычислите площадь ромба ABCD (в см²).

7. На рисунке изображен график производной функции y=f(x), определенной на интервале (−8; 3).



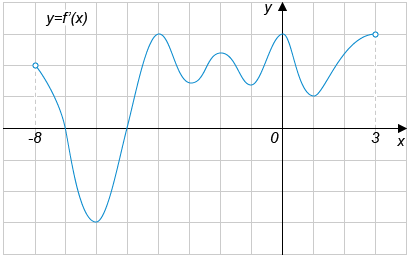
Найдите количество точек, в которых касательная к графику функции параллельна прямой y=−20.

8. Апофема правильной четырехугольной пирамиды равна 2√3 см и наклонена под углом 60∘ к площади основания. Найдите объем пирамиды.

Часть 2

9. Вычислите log₃4⋅log₄5⋅log₅7⋅log₇81

10. Для одного из предприятий-монополистов зависимость объёма спроса на продукцию q (единиц в месяц) от её цены p (тыс. руб.) задаётся формулой: . Определите максимальный уровень цены p (в тыс. руб.), при котором значение выручки предприятия за месяц составит не менее 360 тыс. руб.

11. К резервуару объёмом 220 литров ведут две трубы, первая пропускает на 9 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар она заполняет на 9 минут дольше, чем вторая труба?

12. Найдите наименьшее значение функции на отрезке

13. а) Решите уравнение 6(sin 𝑥 + cos 𝑥) − 2 sin 𝑥 cos 𝑥 + 6 = 0

б) Найдите все корни этого уравнения, принадлежащие промежутку [− 3𝜋/ 2 ; 0].

14. В правильном тетраэдре ABCD, на ребре DC выбрана точка M, такая что, DM:MC=1:2, а на ребре DB выбрана точка N, причем BN:ND=1:2.

а) постройте сечение тетраэдра плоскостью, проходящей через точки M, N и К, где К середина ребра AC.

б) найдите площадь сечения, если все ребра тетраэдра равны 3.

15. Решите неравенство 𝑙𝑜𝑔₃ (𝑥 − 1) ∙ 𝑙𝑜𝑔_𝑥−1 (𝑥 + 1) > 𝑙𝑜𝑔₃ ² (𝑥 + 1)

16. Дана трапеция ABCD (верхнее основание ВС меньше AD) с заданной площадью 𝑆 = 24 и 𝐴𝐷/ 𝐵𝐶 = 3/ 2 . Диагонали трапеции пересекаются в точке О. Средняя линяя трапеции пересекает диагонали в точках M и N.

а) Докажите, что треугольники ABO и COD равновелики;

б) Найти площадь треугольника MNO.

17. Руслан вложил 1 млн. в банк под 16% годовых (начисление в конце года на общую сумму). При этом каждый месяц он снимает по Х тыс. рублей на проживание (начиная со 2 года) в течении 4 лет, и в конце 5 года после начисления процентов сумма оказалась не менее 1 млн. Определите какую максимальную сумму он мог снимать ежемесячно. В ответе укажите целочисленное значение в тысячах рублей?

18. Найдите все значения а, при каждом из которых уравнение

𝑥 ² − 6𝑥 − 7 = 2|𝑥 − 𝑎 + 1| − 16 имеет ровно три различных решения.

19. Может ли произведение цифр натурального числа быть:

а) больше 125 и меньше 131?

б) больше 731 и меньше 737?

в) больше 887 и меньше 894. В случае, если такие значения существуют, то в пункте «а» необходимо указать хотя бы одно значение, в пунктах «б» и «в» все значения.

Вариант №1

</<br>

1. Билет на выставку стоит 200 рублей, а при групповом посещении действует скидка 20 %. Сколько школьников сможет посетить выставку, если родительский комитет выделил на это 2300 рублей?

2. На рисунке жирными точками показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Для наглядности жирные точки соединены линией.

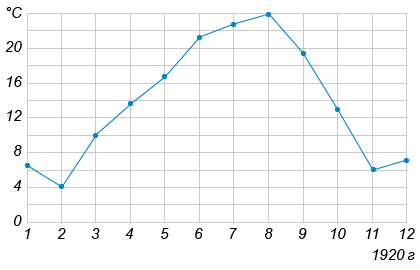
Определите по рисунку разность между наибольшей и наименьшей среднемесячными температурами за указанный период. Ответ дайте в градусах Цельсия.

3. Найдите площадь прямоугольника, изображенного на рисунке.

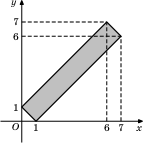
4. Петя бросает игральный кубик. С какой вероятностью на верхней грани выпадет чётное число?

5. Найдите корень уравнения log₅(7−2x) = 3log₅2.

6. С вершины тупого угла B параллелограмма ABCD опущен перпендикуляр BO на сторону AD. Окружность с центром в точке A проходит через вершину B и пересекает сторону AD в точке K. Известно, что AK=6 см, KD=4 см, AO=5 см. Определите периметр параллелограмма ABCD (в см).

7. На рисунке изображён график производной функции f(x), определённой на интервале (−6;5).

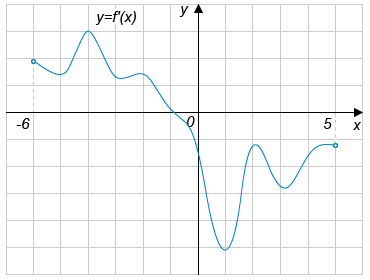
В какой точке отрезка [−5;−1] функция f(x) принимает наименьшее значение?

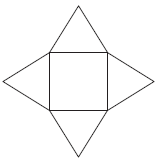
8. На рисунке изображена развёртка пирамиды, состоящая из квадрата со стороной ⁴√12 см и четырёх правильных треугольников. Определите площадь боковой поверхности этой пирамиды (в см2).
   
   

Часть 2

9. Вычислите значение выражения

10. Выехав из города со скоростью v₀=53 км/ч, мотоциклист начинает разгоняться с постоянным ускорением a=8 км/ч². Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением S=v₀ t+at²:2, где t (ч) - время, прошедшее с момента выезда мотоциклиста из города. Через сколько минут мотоциклист доберётся от границы города до автозаправочной станции, расположенной в 42 км от города.

11. Теплоход проходит по течению реки до пункта назначения 280 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 17 км/ч, стоянка длится 6 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч.

12. Найдите наименьшее значение функции y=(x−11)e^x−10 на отрезке [9;11].

13. а) Решите уравнение 3 𝑐𝑜𝑠²𝑥 − 𝑠𝑖𝑛²𝑥 + 2 sin 𝑥 cos 𝑥 = 0

б) Найдите все корни этого уравнения, принадлежащие промежутку [−𝜋; 𝜋/ 2 ].

14. В правильном тетраэдре ABCD, на ребре DC выбрана точка M, такая что, DM:MC=1:4, а на ребре DB выбрана точка N, причем BN:ND=1:4.

а) постройте сечение тетраэдра плоскостью, проходящей через точки M, N и К, где К середина ребра AC.

б) найдите площадь сечения, если все ребра тетраэдра равны 5.

15. Решите неравенство 𝑙𝑜𝑔₅ (𝑥 − 1) ∙ 𝑙𝑜𝑔_𝑥−1 (𝑥 + 3) > 𝑙𝑜𝑔₅ ² (𝑥 + 3)

16. Дана трапеция ABCD (верхнее основание ВС меньше AD) с заданной площадью 𝑆 = 32 и 𝐴𝐷: 𝐵𝐶 = 6: 5 . Диагонали трапеции пересекаются в точке О. Средняя линяя трапеции пересекает диагонали в точках M и N.

а) Докажите, что треугольники ABO и COD равновелики;

б) Найти площадь треугольника MNO.

17. Руслан вложил 1 млн. в банк под 15% годовых (начисление в конце года на общую сумму). При этом каждый месяц он снимает по Х тыс. рублей на проживание (начиная со 2 года) в течении 4 лет, и в конце 5 года после начисления процентов сумма оказалась не менее 1 млн. Определите какую максимальную сумму он мог снимать ежемесячно. В ответе укажите целочисленное значение в тысячах рублей?

18. Найдите все значения а, при каждом из которых уравнение 𝑥 ² − 16 = 2|𝑥 − 𝑎 + 4| − 16 имеет ровно три различных решения.

19. Может ли произведение цифр натурального числа быть:

а) больше 125 и меньше 131?

б) больше 730 и меньше 737?

в) больше 886 и меньше 894. В случае, если такие значения существуют, то в пункте «а» необходимо указать хотя бы одно значение, в пунктах «б» и «в» все значения.