Пояснительная записка

Материалы для рабочей программы составлены на основе:

• федерального государственного стандарта основного общего образования второго поколения,

• примерной программы по математике основного общего образования,

• федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2013-14 учебный год,

• с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования,

• примерной программы общеобразовательных учреждений по математике 7-9 классы,

• базисного учебного плана 2013 года.

Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и даёт примерное распределение учебных часов по разделам курса.

Преподавание данного учебного предмета реализуется на базовом уровне.

Цели обучения алгебре в 7 классах определены следующим образом:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношение к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

В ходе обучения алгебре по данной программе с использованием учебника и методического пособия для учителя, решаются следующие задачи:

• развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и др.);

• усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач;

• осуществление функциональной подготовки учащихся;

• овладение конкретными знаниями необходимыми для применения в практической деятельности;

• выявление и развитие математических способностей, интеллектуального развития ученика.

Общая характеристика учебного предмета.

Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.

В ходе освоения содержания курса учащиеся получают возможность:

• сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

• овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

• изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

• развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

• сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

В ходе преподавания алгебры в 7 классах, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:

• планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;

• решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

• исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;

• ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;

• проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;

• поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

Рабочая программа по алгебре для 7 класса составлена на основе учебно - методического комплекта:

1. А.Г. Мордкович. Алгебра-7. Часть 1: Учебник для общеобразовательных учреждений - М.: Мнемозина, 2013.

2. А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. Алгебра-7. Часть 2: Задачник для общеобразовательных учреждений - М.: Мнемозина, 2013.

3. А.Г. Мордкович. Алгебра, 7-9. Пособие для учителей - М.: Мнемозина, 2013.

4. Ю.П. Дудницын, Е.Е. Тульчинская. Алгебра-7. Контрольные работы (под ред. А.Г. Мордковича) - М: Мнемозина, 2013.

5. А.Г. Мордкович, Е.Е. Тульчинская. Алгебра 7-9. Тесты. - М: Мнемозина, 2012.

6. Л.А. Александрова. Алгебра-7. Самостоятельные работы (под ред. А.Г. Мордковича) - М: Мнемозина, 2012.

7. Е.Е. Тульчинская. Алгебра-7. Блиц-опрос - М.: Мнемозина, 2012

8. Контрольно - измерительные материалы. Алгебра: 7 класс/ Сост. Л.И. Мартышова. - М.: ВАКО,2012.

Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и показывает распределение учебных часов по разделам курса. Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение алгебры в 7 классе отводится 102 часа из расчета 3 часа в неделю. Рабочая программа по алгебре для 7 «б» и 7 «в» классов рассчитана на это же количество часов.

С учетом требований Федерального государственного образовательного стандарта основного общего образования в содержании рабочей программы предполагается реализовать компетентностный, личностно ориентированный и деятельностный подходы, которые определяют задачи обучения: приобретение математических знаний и умений; освоение универсальных учебных действий.

Компетентностный подход определяет следующие особенности предъявления содержания образования: оно представлено в виде трех тематических блоков, обеспечивающих формирование компетенций. В первом блоке представлены дидактические единицы, обеспечивающие совершенствование математических навыков. Во втором - дидактические единицы, которые содержат сведения из истории математики. Это содержание обучения является базой для развития коммуникативной компетенции учащихся. В третьем блоке представлены дидактические единицы, отражающие информационную компетенцию и обеспечивающие развитие учебно-познавательной и рефлексивной компетенций. Таким образом, рабочая программа обеспечивает взаимосвязанное развитие и совершенствование ключевых, общепредметных и предметных компетенций.

Принципы отбора содержания связаны с преемственностью целей образования на различных ступенях и уровнях обучения, логикой внутрипредметных связей, а также с возрастными особенностями развития учащихся.

Личностная ориентация образовательного процесса выявляет приоритет воспитательных и развивающих целей обучения. Способность учащихся понимать причины и логику развития математических процессов открывает возможность для осмысленного восприятия всего разнообразия мировоззренческих, социокультурных систем, существующих в современном мире. Система учебных занятий призвана способствовать развитию личностной самоидентификации, гуманитарной культуры школьников, их приобщению к естественно-математической культуре, усилению мотивации к социальному познанию и творчеству, воспитанию личностно и общественно востребованных качеств, в том числе гражданственности, толерантности.

Деятельностный подход отражает стратегию современной образовательной политики: необходимость воспитания человека и гражданина, интегрированного в современное ему общество, нацеленного на совершенствование этого общества. Система уроков сориентирована не столько на передачу готовых знаний, сколько на формирование активной личности, мотивированной к самообразованию, обладающей достаточными навыками и психологическими установками к самостоятельному поиску, отбору, анализу и использованию информации. Это поможет выпускнику адаптироваться в мире, где объем информации растет в геометрической прогрессии, где социальная и профессиональная успешность напрямую зависят от позитивного отношения к новациям, самостоятельности мышления и инициативности, от готовности проявлять творческий подход к делу, искать нестандартные способы решения проблем, конструктивно взаимодействовать с людьми.

Основой целеполагания является обновление требований к уровню подготовки выпускников в системе естественно-математического образования, отражающее важнейшую особенность педагогической концепции государственного стандарта - переход от суммы «предметных результатов» (то есть образовательных результатов, достигаемых в рамках отдельных учебных предметов), к межпредметным и интегративным результатам. Такие результаты представляют собой обобщенные способы деятельности, которые отражают специфику не отдельных предметов, а ступеней общего образования. В государственном стандарте они зафиксированы как универсальные учебные действия, что предполагает повышенное внимание к развитию межпредметных связей курса математики.

Дидактическая модель обучения и педагогические средства отражают модернизацию основ учебного процесса, их переориентацию на достижение конкретных результатов в виде сформированных регулятивных, коммуникативных и познавательных учебных умений. Формирование целостных представлений о математике будет осуществляться в ходе творческой деятельности учащихся на основе личностного осмысления математических фактов и явлений. Особое внимание уделяется познавательной активности учащихся, их мотивированности к самостоятельной учебной работе. Это предполагает все более широкое использование нетрадиционных форм уроков, в том числе методики деловых и ролевых игр, проблемных дискуссий, межпредметных интегрированных уроков и т.д.

Планируется использование следующих технологий в преподавании предмета:

• Технологии полного усвоения;

• Технологии обучения на основе решения задач;

• Технологии обучения на основе схематических и новых знаковых моделей.

Для естественно - математического образования приоритетным можно считать развитие умений самостоятельно и мотивированно организовывать свою познавательную деятельность, использовать элементы причинно-следственного и структурно-функционального анализа, определять сущностные характеристики изучаемого объекта, самостоятельно выбирать критерии для сравнения, сопоставления, оценки и классификации объектов - в программе это является основой для целеполагания.

На ступени основной школы задачи учебных занятий ( в схеме - планируемый результат) определены как закрепление умений разделять процессы на этапы, звенья, выделять характерные причинно - следственные связи, определять структуру объекта познания, значимые функциональные связи и отношения между частями целого, сравнивать, сопоставлять, классифицировать, ранжировать объекты по одному или нескольким предложенным основаниям, критериям. Принципиальное значение в рамках курса приобретает умение различать факты, мнения, доказательства, гипотезы, аксиомы.

При выполнении творческих работ формируется умение определять адекватные способы решения учебных задач на основе заданных алгоритмов, комбинировать известные алгоритмы деятельности в ситуациях, не предполагающих стандартного применения одного из них, мотивированно отказываться от образца деятельности, искать оригинальные решения.

Учащиеся должны приобрести умения по формированию собственного алгоритма решения познавательных задач, уметь формулировать проблему и цели своей работы, определять адекватные способы и методы решения задачи, прогнозировать ожидаемый результат и сопоставлять его с собственными математическими знаниями. Учащиеся должны научиться представлять результаты индивидуальной и групповой познавательной деятельности в формах конспекта, реферата, рецензии.

Реализация рабочей программы обеспечивает освоение коммуникативных учебных действий, в том числе способностей передавать содержание текста в сжатом и развернутом виде в соответствии с целью учебного задания, проводить информационно-смысловой анализ текста, составлять план, тезисы, конспект. На уроках учащиеся более уверенно овладеют монологической и диалогической речью, умением вступать в речевое общение, участвовать в диалоге ( понимать точку зрения собеседника, признавать право на иное мнение), научатся приводить примеры, подбирать аргументы, перефразировать мысль, формулировать выводы. Для решения познавательных и коммуникативных задач учащимся предлагается использовать различные источники информации, включая энциклопедии, словари, Интернет-ресурсы и другие базы данных, в соответствии с коммуникативной задачей, сферой и ситуацией общения осознанно выбирать выразительные средства языка и знаковые системы.

В процессе обучения должно быть сформировано умение формулировать свои мировоззренческие взгляды как основа духовно-нравственного развития школьника.

Рабочая программа предусматривает следующие варианты дидактико-технологического обеспечения учебного процесса: кабинет для проведения уроков математики, стол для учителя, столы для учащихся, стулья, доска трёхэлементная, наглядные пособия для курса математики, модели геометрических тел, таблицы, чертёжные принадлежности и инструменты. Для информационно-компьютерной поддержки учебного процесса используются: компьютер, сканер, интерактивная доска, презентации, проекты учащихся и учителей; программно-педагогические средства, а также рабочая программа, справочная литература, учебники (по количеству учащихся), разноуровневые тесты взяты из методической литературы: Александрова Л.А. Алгебра. 7 класс. Контрольные работы для учащихся общеобразовательных учреждений / Л.А.Александрова: под ред. А.Г.Мордковича. - М.: Мнемозина, 2012 (по количеству учащихся), тексты самостоятельных и контрольных работ, задания для проектной деятельности.

Нормы оценки знаний, умений и навыков обучающихся по математике.

1. Оценка письменных контрольных работ обучающихся по математике.

Ответ оценивается отметкой «5», если: работа выполнена полностью; в логических рассуждениях и обосновании решения нет пробелов и ошибок; в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях: работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки); допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если: допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если: допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если: работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

2.Оценка устных ответов обучающихся по математике

Ответ оценивается отметкой «5», если ученик: полно раскрыл содержание материала в объеме, предусмотренном программой и учебником; изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности; правильно выполнил рисунки, чертежи, графики, сопутствующие ответу; показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания; продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков; отвечал самостоятельно, без наводящих вопросов учителя; возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков: в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа; допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя; допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях: неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике); имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя; ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме; при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях: не раскрыто основное содержание учебного материала; обнаружено незнание учеником большей или наиболее важной части учебного материала; допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится, если: ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.

3. Общая классификация ошибок.

При оценке знаний, умений и навыков учащихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки: незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения; незнание наименований единиц измерения; неумение выделить в ответе главное; неумение применять знания, алгоритмы для решения задач; неумение делать выводы и обобщения; неумение читать и строить графики; неумение пользоваться первоисточниками, учебником и справочниками; потеря корня или сохранение постороннего корня; отбрасывание без объяснений одного из них; равнозначные им ошибки; вычислительные ошибки, если они не являются опиской; логические ошибки.

3.2. К негрубым ошибкам следует отнести: неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными; неточность графика; нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными); нерациональные методы работы со справочной и другой литературой; неумение решать задачи, выполнять задания в общем виде.

3.3. Недочетами являются: нерациональные приемы вычислений и преобразований; небрежное выполнение записей, чертежей, схем, графиков.

Национально-региональный компонент

Данный фактор является основной причиной большой проблемы определения национально-регионального компонента в Республике Бурятия. Попытки решения данной проблемы конкретно выражаются в увеличении объема знаний на основе введения предметов, отражающих национально-региональные особенности. Вследствие этого возникает диспропорция роста знания и роста возможности их усвоения учащимися. Необходимо отметить, что в данном случае развитие памяти не может определяться развитием уровня познания. Известно, что память измеряется мерой обобщенности знаний (Давыдов В.В. и др.), количеством относительно изолированных логических блоков (Эрдниев П.М.).

Отсутствие целенаправленных действий в процессе обобщения знаний национально-региональной направленности до поры до времени не ощущается как недостаток. Однако сейчас обстоятельства изменились: такое обобщение необходимо в интересах овладения учащимися этими знаниями. Поэтому задача гимназии - систематизация накопленного опыта во всех областях нашей культуры - должна приобрести определенный статус, присущий важнейшим вопросам развития образования нашей республики.

Процесс обобщения и систематизации знаний национально-региональной направленности обладает определенной степенью приближенности, которая должна соответствовать требованиям времени. Такого соответствия в данный момент нет. На наш взгляд, в первую очередь, решение проблемы должно начинаться с создания определения уровня общей картины мира (Бурятия) как системы взаимодействующих, постоянно развивающихся и качественно преобразующихся материальных и духовных реальностей. Говоря об общей картине части мира, мы имеем судьбы единого людского рода и раскрытие их взаимосвязей через путь бурятского народа, понимаемого в широком смысле. Известно, что философия рассматривает версии путей, которыми идет род человеческий. Что есть циклическое движение, линейное и синергетическое.

Думается, что разнообразие подходов к созданию общей картины мира позволит глубже и шире проникнуть в судьбы единого человеческого рода.

Развитие принципа обобщения и систематизации накопленного опыта предлагает, таким образом, постоянное сближение знаний о мире с тем или иным представлением о процессе возникновения общей картины мира.

Необходимо отметить, что система накопленных знаний во всех областях культуры не должна рассматриваться как уже годовая программа для их усвоения. Данную систему можно принять как средство построения такой программы.

В "Программе стабилизации и развития российского образования в переходный период" (март 1991 год) задача регионализации образования была выделена как одна из приоритетных направлений образовательной реформы.

Обновление содержания образования и воспитания предполагает учет национальных, региональных и местных социокультурных особенностей. Восстановление многовековой народной мудрости направлено на развитие духовной и нравственно-эстетической культуры человека. Становятся приоритетными этнопедагогические концепции, проекты, программы.

Содержание образования в школе, включающее этнокультурный компонент, позволяет обеспечивать приобщение учащихся к самобытности народов Байкальского региона и реализуется через учебный план и программу внеклассной воспитательной работы.

Вариативная часть содержания образования представлена модулями, соответствующими образовательным областям с учетом ведущей экспериментальной проблемы школы и национально-регионального компонента.

Включение в учебные предметы национально-регионального компонента направлено на формирование этнокультуроведческой компетенции:

• владение бурятским языком как "средством познания истории народа, его духа";

• умение расшифровывать коды родной культуры;

• знание особенностей природы, хозяйства, общественных отношений;

• системное знание национальных процессов;

• самоидентификация с этносом;

• национальное самоосознание личности в поликультурном пространстве;

• толерантность, уважение инокультурных традиций и обычаев.

Принцип региональности, заключающийся в опоре на культурные достижения, национальные традиции, нравственно-ценностные взгляды родного народа является одним из важных принципов в образовании.

ВКЛЮЧЕНИЕ НАЦИОНАЛЬНО-РЕГИОНАЛЬНОГО КОМПОНЕНТА В СОДЕРЖАНИЕ ОБУЧЕНИЯ МАТЕМАТИКЕ

1. Расстояние между г. Улан-Удэ и районным центром Кижингой 170 км. Из г. Улан-Удэ и Кижинги одновременно навстречу друг другу выехали два автомобиля со скоростью 50 км/ч. и 35 км/ч. Через какое время автомобили встретятся?

2. На кондитерской фабрике "Амта" выпускают конфеты "Ласточка", "Водопад ", "Маска". В 10 минут выпускается 150 конфет "Маска", 200 конфет "Ласточка" и 140 "Водопад". Какую часть из выпускаемых конфет составляют конфеты каждого сорта?

3. Улан-Удэнское ателье "Элегант" за месяц должно сшить 38 костюмов. В первую неделю было сшито 7 костюмов, во вторую - 11 костюмов. Какую часть всех костюмов осталось сшить?

4. Из 18 маралов, занесенных в "Красную книгу Бурятии" 5 были самками, а остальные-самцы. Какую часть всех маралов составляли самки?

5. Со станции Горхон вышел поезд со скоростью 48 км/час. Через 2 часа с той же станции в противоположном направлении вышел другой поезд Москва-Пекин, и через 3 часа после его выхода расстояние между поездами стало 402 км. Найти скорости поездов Улан-Удэ - Горхон и Москва - Пекин.

Программа является примерной и позволяет учителю самостоятельно распределять материал и время для его повторения и обобщения в зависимости от степени подготовленности учащихся.

В течение года возможны коррективы рабочей программы, связанные с объективными причинами.

Результаты обучения

Результаты обучения представлены в Требованиях к уровню подготовки, задающих систему итоговых результатов обучения, которые должны быть достигнуты всеми учащимися, оканчивающими 7 класс, и достижение которых является обязательным условием положительной аттестации ученика за курс 7 класса. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни».

Требования к уровню подготовки обучающихся

В результате изучения ученик должен

знать/понимать:

• существо понятия математического доказательства; приводить примеры доказательств;

• существо понятия алгоритма; приводить примеры алгоритмов;

• как используются математические формулы, уравнения, примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

уметь:

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• выполнять основные действия со степенями с натуральными показателями, с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования выражений;

• решать линейные уравнения и сводящиеся к ним, системы двух линейных уравнений;

• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• изображать числа точками на координатной прямой; определять координаты точки плоскости, строить точки с заданными координатами;

• строить графики изученных функций;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• определять простейшие свойства функции по ее графику; применять графические представления при решении уравнении, систем, описывать свойства изученных функций, строить их графики;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;

• интерпретации графиков зависимостей между величинами.

Содержание тем учебного курса

Математический язык. Математическая модель (9 ч)

Числовые и алгебраические выражения. Переменная. Допустимое значение переменной. Недопустимое значение переменной. Первые представления о математическом языке и о математической модели. Линейные уравнения с одной переменной. Линейные уравнения как математические модели реальных ситуаций. Координатная прямая, виды промежутков на ней.

Степень с натуральным показателем (8 ч)

Степень. Основание степени. Показатель степени. Свойства степени с натуральным показателем. Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем.

Одночлены. Операции над одночленами (10 ч)

Одночлен. Коэффициент одночлена. Стандартный вид одночлена. Подобные одночлены.

Сложение одночленов. Умножение одночленов. Возведение одночлена в натуральную степень. Деление одночлена на одночлен.

Многочлены. Арифметические операции над многочленами (16 ч)

Многочлен. Члены многочлена. Двучлен. Трехчлен. Приведение подобных членов многочлена. Стандартный вид многочлена.

Сложение и вычитание многочленов. Умножение многочлена на одночлен. Умножение многочлена на многочлен.

Квадрат суммы и квадрат разности. Разность квадратов. Разность кубов и сумма кубов.

Деление многочлена на одночлен.

Разложение многочленов на множители (17 ч)

Вынесение общего множителя за скобки. Способ группировки. Разложение многочлена на множители с помощью формул сокращенного умножения, комбинации различных приемов. Метод выделения полного квадрата.

Понятие алгебраической дроби. Сокращение алгебраической дроби.

Тождество. Тождественно равные выражения. Тождественные преобразования.

Линейная функция (15 ч)

Координатная плоскость. Алгоритм отыскания координат точки. Алгоритм построения точки М (а; b) в прямоугольной системе координат.

Линейное уравнение с двумя переменными. Решение уравнения ах + by + с = 0. График уравнения. Алгоритм построения графика уравнения ах + by + с = 0.

Линейная функция. Независимая переменная (аргумент). Зависимая переменная. График линейной функции. Наибольшее и наименьшее значения линейной функции на заданном промежутке. Возрастание и убывание линейной функции.

Линейная функция у = kx и ее график.

Взаимное расположение графиков линейных функций.

Функция у = х² (8 ч)

Функция у = х², ее свойства и график. Функция у = - х², ее свойства и график.

Графическое решение уравнений. Кусочная функция. Чтение графика функции. Область определения функции. Первое представление о непрерывных функциях. Точка разрыва. Разъяснение смысла записи у = f(x). Функциональная символика.

Системы двух линейных уравнений с двумя переменными (13 ч)

Система уравнений. Решение системы уравнений. Графический метод решения системы уравнений. Метод подстановки. Метод алгебраического сложения.

Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи).

Обобщающее повторение (6 ч)

Структура курса

№

Модуль (глава)

Количество часов

1

Математический язык. Математическая модель

9

2

Линейная функция

15

3

Системы двух линейных уравнений с двумя переменными

13

4

Степень с натуральным показателем и ее свойства

8

5

Одночлены. Арифметические операции над одночленами

10

6

Многочлены. Арифметические операции над многочленами

16

7

Разложение многочленов на множители

17

8

Функция y = x²

8

Обобщающее повторение

6

Годовой календарный график текущего контроля

№

№ урока

Контрольная работа

Количество часов

1

8

Контрольная работа №1. «Математический язык. Математическая модель»

1

2

23

Контрольная работа №2 на тему «Линейная функция»

1

3

36

Контрольная работа №3 «Системы двух линейных уравнений с двумя переменными»

1

4

44

Контрольная работа №4 «Степень с натуральным показателем и ее свойства»

1

5

54

Контрольная работа №5. «Одночлены. Арифметические операции над одночленами»

1

6

63

Контрольная работа №6. «Многочлены. Арифметические операции над многочленами»

1

7

70

Контрольная работа №7. «Формулы сокращенного умножения.»

1

8

83

Контрольная работа №8 на тему «Разложение многочленов на множители»

1

9

95

Контрольная работа №9 на тему «Функция »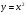

1

10

100

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА №10

1

КАЛЕНДАРНО ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

№ п\п

Тема урока

Количество часов

Домашнее задание

Контроль

Математический язык. Математическая модель

9

1-3

Числовые и алгебраические выражения

3

Работа со справочной литературой. Решение задач

С/р №1, 2

4-5

Что такое математический язык

2

Самостоятельный поиск информации в различных источниках. Решение задач

С/р №3

6-7

Что такое математическая модель

2

Использование справочной литературы, а также Интернет. Решение задач

С/р №4

8

Контрольная работа №1. «Математический язык. Математическая модель»

1

Создание базы тестовых заданий по теме

Индивидуальное

решение контрольных заданий.

9

Резерв

1

Линейная функция

15

10-11

Координатная прямая

2

Изучение дополнительной литературы. Решение задач

С/р №5

12-13

Координатная плоскость

2

Поиск нужной информации по заданной теме. Решение задач

С/р №6

14-16

Линейное уравнение с двумя переменными и его график

3

Составление обобщающих информационных таблиц . Решение задач

С/р №7

17-18

Линейная функция и ее график

2

Работа со справочной литературой. Решение задач

С/р №8, 9, 10

19-20

Линейная функция y = kx

2

Использование справочной литературы, а также Интернет. Решение задач

С/р №11

21-22

Взаимное расположение графиков линейных функций

2

Изучение дополнительной литературы. Решение задач

23

Контрольная работа №2 на тему «Линейная функция»

1

Создание базы тестовых заданий по теме

Индивидуальное

решение контрольных заданий.

24

Резерв

1

Системы двух линейных уравнений с двумя переменными

13

25-26

Основные понятия

2

Работа со справочной литературой. Решение задач

С/р №12

27-29

Метод подстановки

3

Изучение дополнительной литературы. Решение задач

С/р №13, 14

30-32

Метод алгебраического сложения

3

С/р №15, 16

33-35

Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций

3

Составление обобщающих информационных таблиц . Решение задач

С/р №17

36

Контрольная работа №3 «Системы двух линейных уравнений с двумя переменными»

1

Создание базы тестовых заданий по теме

Индивидуальное

решение контрольных заданий.

37

Резерв

1

Степень с натуральным показателем и ее свойства

8

38

Что такое степень с натуральным показателем

1

Работа со справочной литературой. Решение задач

С/р №18

39

Таблицы основных степеней

1

Составление обобщающих информационных таблиц . Решение задач

С/р №19

40

Свойства степени с натуральным показателем

1

Изучение дополнительной литературы. Решение задач

С/р №20

41-42

Умножение и деление степеней с одинаковыми показателями

2

Использование справочной литературы, а также Интернет. Решение задач

С/р №21

43

Степень с нулевым показателем

1

Самостоятельный поиск информации в различных источниках. Решение задач

44

Контрольная работа №4 «Степень с натуральным показателем и ее свойства»

1

Создание базы тестовых заданий по теме

Индивидуальное

решение контрольных заданий.

45

Резерв

1

Одночлены. Арифметические операции над одночленами

10

46-47

Понятие одночлена. Стандартный вид одночлена

2

Изучение дополнительной литературы. Решение задач

С/р №22

48-49

Сложение и вычитание одночленов

2

Использование справочной литературы, а также Интернет. Решение задач

С/р №23

50-51

Умножение одночленов. Возведение одночлена в натуральную степень

2

Работа со справочной литературой. Решение задач

С/р №24

52-53

Деление одночлена на одночлен

2

Самостоятельный поиск информации в различных источниках. Решение задач

С/р №25

54

Контрольная работа №5. «Одночлены. Арифметические операции над одночленами»

1

Создание базы тестовых заданий по теме

Индивидуальное

решение контрольных заданий.

55

Резерв

1

Многочлены. Арифметические операции над многочленами

16

56

Основные понятия

1

Изучение дополнительной литературы. Решение задач

С/р №26

57-58

Сложение и вычитание многочленов

2

Работа со справочной литературой. Решение задач

С/р №27

59-60

Умножение многочлена на одночлен

2

Самостоятельный поиск информации в различных источниках. Решение задач

С/р №28, 29

61-62

Умножение многочлена на многочлен

2

Составление обобщающих информационных таблиц . Решение задач

С/р №30

63

Контрольная работа №6. «Многочлены. Арифметические операции над многочленами»

1

Создание базы тестовых заданий по теме

Индивидуальное

решение контрольных заданий.

64-65

Формулы сокращенного умножения. Квадрат суммы и квадрат разности

2

Использование справочной литературы, а также Интернет. Решение задач

С/р №31

66

Формулы сокращенного умножения. Разность квадратов

1

Работа со справочной литературой. Решение задач

С/р №32

67

Формулы сокращенного умножения. Разность кубов и сумма кубов

1

Изучение дополнительной литературы. Решение задач

С/р №33

68-69

Деление многочлена на одночлен

2

70

Контрольная работа №7. «Формулы сокращенного умножения.»

1

Создание базы тестовых заданий по теме

Индивидуальное

решение контрольных заданий.

71

Резерв

1

Разложение многочленов на множители

17

72

Что такое разложение многочлена на множители и зачем оно нужно

1

Работа со справочной литературой. Решение задач

73-74

Вынесение общего множителя за скобки

2

Использование справочной литературы, а также Интернет. Решение задач

С/р №34

75-77

Способ группировки

3

Составление обобщающих информационных таблиц . Решение задач

С/р №35

78-81

Разложение многочлена на множители с помощью формул сокращенного умножения

4

Изучение дополнительной литературы. Решение задач

С/р №36,37, 38

82

Разложение многочленов на множители с помощью комбинации различных приемов

1

Самостоятельный поиск информации в различных источниках. Решение задач

С/р №39

83

Контрольная работа №8 на тему «Разложение многочленов на множители»

1

Создание базы тестовых заданий по теме

Индивидуальное

решение контрольных заданий.

84

Резерв

1

85-87

Сокращение алгебраических дробей

3

Работа со справочной литературой. Решение задач

С/р №40

88

Тождества

1

Изучение дополнительной литературы. Решение задач

Функция y = x²

8

89-90

Функция y = x² и её график

2

Самостоятельный поиск информации в различных источниках. Решение задач

С/р №41

91-92

Графическое решение уравнений

2

Изучение дополнительной литературы. Решение задач

С/р №42

93-94

Что означает в математике запись y = f(x)

2

Работа со справочной литературой. Решение задач

С/р №5

95

Контрольная работа №9 на тему «Функция »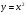

1

Создание базы тестовых заданий по теме

Индивидуальное

решение контрольных заданий.

96

Резерв

1

Обобщающее повторение

6

97

Повторение. Степень с натуральным показателем.

1

Изучение дополнительной литературы. Решение задач

Карточки

98

Повторение. Одночлены.

1

Самостоятельный поиск информации в различных источниках. Решение задач

Карточки

99

Повторение. Многочлены.

1

Использование справочной литературы, а также Интернет. Решение задач

100

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА №10

1

Создание базы тестовых заданий по теме

Индивидуальное

решение контрольных заданий.

101

Повторение. Разложение многочленов на множители.

1

Работа со справочной литературой. Решение задач

Тест

102

Повторение. Системы двух линейных уравнений с двумя переменными.

1

Тест

Литература для учителя

1. Алгебра. Тесты для промежуточной аттестации. 7-8 класс. Издание второе, переработанное. Под редакцией Ф.Ф. Лысенко. Ростов-на-Дону: Легион, 2012. - 160 с.

2. Государственный стандарт основного общего образования по математике.

3. Дидактические материалы по алгебре для 7 класса - 5-е изд., перераб. Гусев В.А., Медяник А.И. - М.: Просвещение,

4. Задачи повышенной трудности в курсе алгебры 7-9 классов: Книга для учителя. Н.П. Кострикина. - М.: Просвещение

5. История математики в школе. VII-VIII кл. Пособие для учителей. / Г.И. Глейзер - М.: Просвещение

6. Контрольные и самостоятельные работы по алгебре: 7 класс: к учебнику А.Г. Мордковича и др. "Алгебра. 7 класс" / М.А. Попов. - 2-е изд., стереотип. - М.: Издательство «Экзамен», 2013. - 63 с.

7. Программы. Математика. 5-11 классы / авт.-сост. И.И. Зубарева, А.Г. Мордкович. - М. Мнемозина, 2013. - 64 с.

8. Рубежный контроль по математике: 5-9 классы / Р. Изместьева. - М.: Чистые пруды, 2012. - 32 с.

9. Учебный мультимедиа-продукт к учебнику и задачнику А.Г. Мордковича «Алгебра». 7 класс. - М.: Издательство «Мнемозина», 2012.

Литература для учащихся

1. Дидактические материалы по алгебре для 7 класса - 5-е изд., перераб. Гусев В.А., Медяник А.И. - М.: Просвещение.

2. История математики в школе. VII-VIII кл. Пособие для учителей. / Г.И. Глейзер - М.: Просвещение

Для обеспечения плодотворного учебного процесса предполагается использование информации и материалов следующих Интернет-ресурсов:

Министерство образования РФ: ; ;

Тестирование online: 5-11 классы:

Педагогическая мастерская, уроки в Интернет и многое другое: , , , , , , , ,

Новые технологии в образовании:

Путеводитель «В мире науки» для школьников:

Мегаэнциклопедия Кирилла и Мефодия:

Сайты «Мир энциклопедий», например: ;

Для информационно-компьютерной поддержки учебного процесса предполагается использование следующих программно-педагогических средств, реализуемых с помощью интерактивного комплекса:

1. CD «1С: Репетитор. Математика» (КиМ);

2. CD Математика, 5-11.

3. CD Математика, 5-11. Практикум

4. CD Уроки алгебры 7-8 Виртуальная школа Кирилла и Мифодия

5. СD Электронное сопровождение курса Алгебра 7, под ред. А.Г. Мордковича, Издательство «Мнемозина»

6. CD Алгебра 7-9. Поурочные планы. Издательство «Учитель»