Олимпиада по математике 6-11 классы

Олимпиадные задания по математике

5-11 классов

Большезадоевская СОШ

Руководитель МО: Рамазанова А.К.

5 класс

Задача 1 :

Стороны четырёхугольника ABCD равняются: AB = 11, BC = 7, CD = 9, AD = 3, а углы A и C - прямые.

Чему равна площадь четырёхугольника?



Задача 2 :

Коробку размером 30 х 30 х 50 нужно наполнить одинаковыми кубиками.

Какое минимальное количество кубиков позволит это сделать?



Задача 3:

Комнаты отеля пронумерованы тремя цифрами. Первая цифра обозначает этаж, а следующие две - номер комнаты. Например, 125 означает 25 ю комнату на первом этаже.

В отеле 5 этажей, они пронумерованы от 1 до 5, с 35 комнатами, пронумерованными от 101 до 135 на первом этаже и аналогичным образом - на остальных.

Сколько раз при нумерации комнат использовали цифру 2?

Задача 4:

Ваня, Коля и Антон могут одинаково быстро вскопать землю лопатой.

Если любые два из этих мальчиков будут работать вместе, то справятся с земельным участком за полтора часа.

За какое время ребята вскопают тот же участок, если будут работать все трое вмест.



Задача 5:

В записи (88888888) нужно поставить знаки сложения таким образом, чтобы получилась сумма, которая будет равна 1000.

6 класс

Задача 1:

Разность двух чисел на 17 меньше уменьшаемого и на 9 больше вычитаемого.

Найдите уменьшаемое и вычитаемое.



Задача 2:

Будет ли сумма чисел 1 + 2 + 3 + ......+ 2005 + 2006 + 2007 делиться на 2007?

Ответ обоснуйте.



Задача 3:

Нужно разместить 17 кроликов так, чтобы в каждой клетке было разное количество кроликов.

Какое наибольшее число клеток понадобится?



Задача 4:

На выставку привезли 25 собак. 12 из них большие, 8 маленькие, остальные средние.

Только 10 из участников выставки породистые, остальные дворняжки.

Среди дворняжек поровну больших, маленьких и средних.

Сколько больших породистых собак привезли на выставку?



Задача 5:

Все треугольники, изображенные на рисунке, имеют равные стороны.

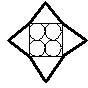Радиус каждой из окружностей равен 2 см.

Окружности касаются друг друга и сторон квадрата.

Чему равен периметр звездочки, нарисованной жирной линией?

7 класс

Задача 1:

Квадрат числа состоит из цифр 0, 2, 3, 5. Найти его.



Задача 2:

Найти натуральное число A , если из трех следующих утверждений два верны, а одно - неверно:

а) A+51 есть точный квадрат,

б) последняя цифра числа A есть единица,

в) A-38 есть точный квадрат.

Задача 3:

Дан угол и точка M внутри него. Провести прямую через эту точку так, чтобы ее отрезок между сторонами угла делился данной точкой пополам.



Задача 4:

Автомобиль из A в B ехал со средней скоростью 50 км/ч., а обратно возвращался со скоростью 30 км/ч.. Какова его средняя скорость?

Задача 5:

В каждой вершине n-угольника стоит одно из чисел +1 или -1. На каждой стороне написано произведение чисел, стоящих на концах этой стороны. Оказалось, что сумма чисел на сторонах равна нулю. Докажите, что

1) n - четно,

2) n делится на 4.

8 класс

Задача 1:

Мальчик пошел с отцом в тир. Отец купил ему 10 пулек. В дальнейшем отец за каждый промах отбирал у сына одну пульку, а за каждое попадание давал одну дополнительную пульку. Сын выстрелил 55 раз, после чего пульки у него кончились. Сколько раз он попал?

Задача 2:

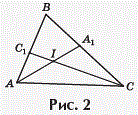
Две биссектрисы треугольника пересекаются под углом 60°. Докажите, что один из углов этого треугольника равен 60°.

Задача 3:

В выпуклом четырехугольнике ABCD стороны AB и CD параллельны, а диагонали AC и BD перпендикулярны. Докажите, что AD+BC = AB+CD.

Задача 4:

В трех кучках лежат соответственно 12, 24 и 19 спичек. За ход можно переложить спичку из одной кучки в другую. За какое наименьшее число ходов можно получить три кучки с 8, 21 и 26 спичками?

Задача 5:

На гранях кубика расставлены 6 различных чисел от 6 до 11. Кубик бросили два раза. В первый раз сумма чисел на четырех боковых гранях оказалась равна 36, во второй - 33. Какое число написано на грани, противоположной той, где написана цифра 10?

9 класс

Задача 1:

Решите неравенство :



Задача 2:

Решите уравнение : x² + 2005x - 2006 = 0.



Задача 3:

Стрелок десять раз выстрелил по стандартной мишени и выбил 90 очков. Сколько попаданий было в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было?

Задача 4:

Можно ли представить дробь 2/7 в виде суммы двух дробей, числители которых равны 1, а знаменатели - различные целые числа? ( 6 баллов)

Задача 5:

На столе лежат 2005 монет. Двое играют в следующую игру: ходят по очереди; за ход первый может взять со стола любое нечетное число монет от 1 до 99, второй любое четное число монет от 2 до 100. Проигрывает тот, кто не сможет сделать ход.

Кто выиграет при правильной игре?

10 класс

Задача 1 :

Докажите, что уравнение x⁴- 4x³ + 12x² - 24 x +24 = 0 не имеет решений.



Задача 2 :

Докажите, что в ходе любого сыгранного футбольного матча был момент, когда одна из команд забила голов столько же, сколько другой осталось забить.



Задача 3 :

Хорда удалена от центра окружности на расстояние h. В каждый из двух сегментов круга, стягиваемый этой хордой, вписан квадрат так, что пара его соседних вершин лежит на хорде, а другая пара соседних вершин - на соответствующей дуге окружности.

Найдите разность длин сторон квадратов.



Задача 4 :

Найдите многочлен с целочисленными коэффициентами, корнем которого является число

√2 + √3.



Задача 5 :

Лист бумаги разрезали на 5 частей, некоторые из этих частей разрезали на 5 частей, и т. д. Может ли за некоторое число разрезаний получиться 2006 листка бумаги?

11 класс

Задача 1 :

Докажите, что произведение четырех последовательных целых чисел, сложенное с единицей, есть точный квадрат.



Задача 2 :

Решите уравнение sin⁴4x + cos²x = 2sin4x х cos⁴x.

Задача 3:

Докажите, что уравнение xy = 2006 (x+y) имеет решения в целых числах.

</ Задача 4 :

Докажите неравенство x² - 3x³< 1/6 на луче [1/4; + ∞).



Задача 5 :

В прямоугольник 20 x 25 бросают 120 квадратов 1 x 1. Докажите, что в прямоугольник можно поместить круг с диаметром, равным 1, не имеющий общих точек ни с одним из квадратов.