- Учителю
- Разработка урока алгебры для 7 класса
Разработка урока алгебры для 7 класса
| ГБОУ Лицей «МКШ им. В.Н. Челомея» |
| Преобразование целого выражения в многочлен |
| Урок алгебры в 7 классе |
Елена Пильтяй
г. Байконур
Тема: Преобразование целого выражения в многочлен.
Цель:
-
научить различать целые и дробные выражения;
-
научить преобразовывать целое выражение в многочлен, применяя тождественные преобразования и формулы сокращённого умножения;
-
прививать интерес к предмету - познакомить с «треугольником Паскаля».
План:
-
Организационный момент.
-
Проверка домашнего задания в виде самостоятельной работы.
-
Объяснение новой темы.
-
Решение задач повышенной сложности (для тех, кто хочет знать больше).
-
Закрепление. Самостоятельная работа.
-
Организационный момент.
2. Самостоятельная работа проводится на два варианта по выбору, (типа УХ) Усвоил, и Хорошо усвоил. На дом было задано два варианта А2 и Б2 из Ершовой А.П. и Голобородько В.В.
Самостоятельная работа составлена по следующему правилу: вариант У состоит из примеров варианта А1, вариант Х - из примеров варианта В1, задачника Ершовой А.П. и Голобородько В.В.
Самостоятельная работа УХ
У
1. Разложите на множители:
а) 2у2-18;
б) 2х2-12х+18.
2. Упростить выражение:
а) (2а+3)(а-3)-2а(4+а);
б) (1-х)(1+х)+(х-1)2
3. Докажите тождество:
х4-27х=(х2-3х)(х2+3х+9).
Х
1. Разложите на множители:
а) х3-ху2-6у2+6х2;
б) 8х4у-ху4.
2. Упростить выражение:
а) (2х+3)(2х-1)-(2х+1)(2х-1);
б) (3а-3в)2-3(а-в)2.
3. Докажите тождество:
(а2+4)2-16а2=(а+2)2(а-2)2.
Х
Для тех учеников, кто справится раньше, подготовить перфокарты на применение формул сокращённого умножения.Ключ к проверке самостоятельной работы:
У
1. Разложите на множители:
а) 2у2-18=2(у-3)(у+3);
б) 2х2-12х+18=2(х2-6х +9)=2(х-3)2.
2. Упростить выражение:
а)(2а+3)(а-3)-2а(4+а)=2а2-6а+3а-8а-2а2=-
=11а;
б) (1-х)(1+х)+(х-1)2=1-х2+х2-2х+1=1-х.
3. Докажите тождество:
х4-27х=(х2-3х)(х2+3х+9).
х(х3-33)=х(х-3)( х2+3х+9)
х(х3-33)= х(х3-33)
Х
1. Разложите на множители:
а) х3-ху2-6у2+6х2=х(х2-у2)+6(х2-у2)=
=(х2-у2)(х+6)=(х-у)(х+у)(х+6);
б) 8х4у-ху4=ху(23х3-у3)=
=ху(2х-у)(4х2+2ху+у2).
2. Упростить выражение:
а) (2х+3)(2х-1)-(2х+1)(2х-1)=
=(2х-1)(2х+3-2х-1)=2(2х-1);
б) (3а-3в)2-3(а-в)2=9(а-в)2-3(а-в)2=
=6(а-в)2=6(а2-2ав+в2).
3. Докажите тождество:
(а2+4)2-16а2=(а+2)2(а-2)2.
(а2+4-4а)(а2+4+4а)= (а+2)2(а-2)2
(а-2)2(а+2)2=(а+2)2(а-2)2.
Х
Проверить первые три работы и дать «консультантам» «ключ» к проверке, они очень быстро проверяют работы остальных учеников.
После чего можно судить о подготовленности учеников к следующей теме. Провести мини анализ: - сколько человек выбрали X! Y!
- сколько «5», «4», «3», «2».
3.
Рассмотреть пример: (х2+2)-(х-2)(х+2)(х2+4)-6х(0,5х-х2)
Разработать алгоритм представления этого выражения в виде многочлена стандартного вида.
Алгоритм.
-
Раскрыть скобки, используя подходящие приёмы (умножение одночлена на многочлен, умножение многочленов, применение формул сокращённого умножения);
-
Привести подобные члены;
-
Записать многочлен в стандартном виде.
Решить из учебника: № 974 - устно; 975 - с комментированием;
976 - на доске; 983 - на доске с комментированием.
4. Задания из учебника (алгебра 7 класс под редакцией С.А. Теляковского)
№ 943, 945, 949, (тождество Диофанта), № 951 (тождество Диофанта
Квантор №6 1991г).
Показать треугольник Паскаля, рассказать о его применении.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
Пример: записать коэффициенты для выражений (а+в)8 и (а-в)10.
5. Самостоятельная работа
I вариант
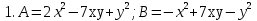 . Найти: а) А+В, б) А-В.
. Найти: а) А+В, б) А-В.
2. Решить уравнение: (3х-5)-(2х-2)=1.
3. Преобразовать в многочлен стандартного вида: (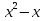 +1)(
+1)(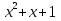 ).
).
4. Какое число надо добавить к многочлену 9х2-60х-2, чтобы получился квадрат двучлена?
II вариант
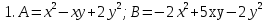 . Найти: а) А+В, б) А-В.
. Найти: а) А+В, б) А-В.
2. Решить уравнение: (5х+4)-(3х-6)=4.
3. Преобразовать в многочлен стандартного вида: (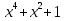 )(
)(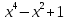 ).
).
4. Какое число надо добавить к многочлену 9х2+30х-3, чтобы получился квадрат двучлена?
6. Домашнее задание. № 981; 984; 989; 1056; 1058 а),в).
Найти коэффициенты (а+в)15;
Сделать перфокарты на применение формул (а+в)3 и (а-в)3; а3+в3 и а3-в3.