- Учителю
- Урок алгебры и начала анализа в 10 классе по теме: Преобразования графиков тригонометрических функций.
Урок алгебры и начала анализа в 10 классе по теме: Преобразования графиков тригонометрических функций.
Методическая разработка урока
по алгебре и началам анализа в 10 классе
Ушаковой Галины Ивановны
учителя математики
1 квалификационной категории
МБОУ «Шкуновская СОШ»
Тема урока: Преобразования графиков тригонометрических функций. Построение графика функции у = mf(x) по известному графику функции у =f(х)
Пояснительная записка
Развитие компьютерной техники, программного обеспечения происходит семимильными шагами и сегодня операционная система Linux прочно завоевывает позиции на компьютерах, ноутбуках и даже нетбуках в том числе и в школе. У Linux есть ещё одно преимущество - её идеология свободного распространения.
В нашей школе внедрение Linux в учебный процесс идёт в течении трёх лет. Приведённая разработка урока ориентирована на учащихся старших классов уже знакомых с работой в Linux. Для проведения урока не требуется устанавливать дополнительных программ достаточно просто подготовить требуемое количество компьютеров с ОС Linux. Универсальная многофункциональная пользовательская система KDesktop 6.0 включает в себя все необходимое для офисной работы, создания различных видов графики и анимации, обработки звука и видео, средства разработки приложений, а также образования.
На компьютере с ОС ALT Linux 6.0.0 KDesktop интерактивная модель движения графика создается с помощью программы построения графиков (KmPlot). Применение интерактивных моделей является одним из наиболее эффективных способов внедрения новых информационных технологий в преподавание математики.
Проведение уроков с использованием информационных технологий - это мощный стимул в обучении. Посредством таких уроков активизируются психические и интеллектуальные процессы учащихся, стимулируется развитие познавательного интереса. В этом и заключается перспективность и актуальность данной разработки урока на тему «Преобразование графиков тригонометрических функций», которая может быть использована учителями для проведения уроков и факультативов, а так же для организации самостоятельной работы учащихся.
Урок алгебры и начала анализа - 10 класс (учитель - Ушакова Г.И.)
Тема урока: Преобразования графиков тригонометрических функций. Построение графика функции у = mf(x) по известному графику функции у =f(х)
Элементы содержания: Растяжение от оси абсцисс с коэффициентом. Сжатие к оси абсцисс с коэффициентом. Построение графика функции у = mf(x) по известному графику функции у =f(х). Преобразование симметрии относительно оси абсцисс
Знать: виды преобразований графиков функций; способ растяжения (сжатия) графика функции у =f(х) от оси абсцисс с коэффициентом т.
Уметь: выполнять преобразования графиков тригонометрических функций
Тип урока: комбинированный урок
-
урок формирования новых знаний, проводится в форме урока-исследования.
Цели урока:
Образовательные цели:
-
Экспериментальным путем с использованием таблиц и компьютера получить алгоритм построения графиков функции y=mf(x) по заданному графику y=f(x)
-
Научиться применять полученный алгоритм для решения подобных задач
Развивающие цели:
-
Формирование умений анализировать, обобщать полученные результаты, проводить исследования
-
Развитие самостоятельности в учебной деятельности.
Оборудование и материалы: компьютеры с установленной ОС ALT Linux 6.0.0 KDesktop, раздаточный материал: карточки с заданиями для самостоятельной работы, презентация к уроку.
Ход урока:
-
Приветствие. Организационный момент. Постановка цели и задачи урока.
- Сегодня нам предстоит повторить уже известные преобразования графиков функций и на основе этих знаний исследовать поведение графиков тригонометрических функций в зависимости от коэффициентов с помощью компьютера.
-
Актуализация опорных знаний: слайд 2.
Задание 1. Построить графики функций y=sin(x -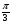 )+1, y=cos(x+
)+1, y=cos(x+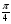 )-2 , объяснить, как можно получить эти графики из графиков функций y=sin x, y=cos x, (у доски работают два ученика).
)-2 , объяснить, как можно получить эти графики из графиков функций y=sin x, y=cos x, (у доски работают два ученика).
Работа анализируется всеми учащимися и оценивается учителем.
II. Организация осознания и восприятия нового материала:
Вводное слово учителя: «Вы уже знаете, как строить графики функций вида y=sin(x+m)+n (y=cos(x+m)+n).
А знаем ли мы способ построения графиков функций y=msinx ( y=mcosx)?
Как вы думаете, изменится график функции y=f(x), если f(x) умножить на m.
Выдвигается гипотеза, как правило, верная.
Учитель: Итак, тема урока: «Преобразования графиков тригонометрических функций. Построение графика функции у = mf(x) по известному графику функции у =f(х)» слайд 3.
Давайте вашу гипотезу проверим. Наша задача на уроке экспериментальным путем получить алгоритм для построения графиков функций вида y= mf(x) или y= mf(x), где f(x)=sinx или f(x)=cosx.
Для этого выполним следующее задание.
Практическая работа: (Приложение 1) слайд 4.
Задание 1. Построить в тетрадях по точкам графики функций y=sin x, y=cos x, заполнить таблицы значений на корточках: 1 вариант для функции y=sin x, а второй - для функции y=cos x и ответить на вопрос: Как изменилось значение функции в каждом из случаев?
x
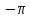
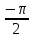
0
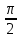
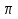
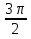
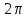
y = 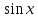
y = 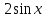
y = 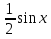
x
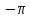
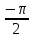
0
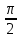
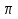
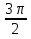
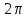
y = 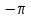
y =2 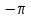
y = 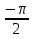
Задание 2. слайды 5, 6. Выясните поведение графиков тригонометрических функций в зависимости от коэффициентов с помощью компьютера. Для этого постройте графики этих функций на компьютере следуя инструкции (Приложение 2), сравните полученные результаты, сделайте вывод, внося соответствующие данные в таблицу:
m
Формула функции
Преобразование графика
2
График функции__________ получается из графика функции ________в результате __________от оси _____
С коэффициентом_______
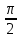
График функции__________ получается из графика функции ________в результате __________от оси _____
С коэффициентом_______
- 1
1. График функции__________ получается из графика функции ________в результате __________от оси _____
с коэффициентом_______
2. подвергнем график функции ________преобразованию ___________относительно оси______
-2
1. График функции__________ получается из графика функции ________в результате __________от оси _____
с коэффициентом_______
2. подвергнем график функции ________преобразованию ___________относительно оси______
- 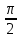
1. График функции__________ получается из графика функции ________в результате __________от оси _____
с коэффициентом_______
2. подвергнем график функции ________преобразованию ___________относительно оси______
Инструкция по выполнению работы на компьютере с ОС ALT Linux 6.0.0 KDesktop (Приложение 2). слайд 7.
-
Меню запуска приложений - образование - математика - программа построения графиков (KmPlot)
-
графики - добавить - график в декартовых координатах - редактор выражений - вставить функцию - выбираем cos или sin - переменная в скобках (x) - enter (это основная функция для сравнения)
-
аналогично добавить ещё один график функции f(x)=cosx или f(x)=sinx в этом графике и будем менять коэффициенты чтобы получить графики функций: f(x)=2cosx или f(x)=2sinx
f(x)=0,5cosx или f(x)=0,5sinx
f(x)= -2cosx или f(x)= - 2sinx
f(x)= - 0,5cosx или f(x)= - 0,5sinx
-
Проанализируйте расположение графиков этих функций относительно друг друга, относительно осей координат.
-
Установите связь между аналитической записью функции и преобразованием графика этой функции.
-
Сформулируйте вывод по проделанной работе.
-
Попробуйте составить алгоритм построения графиков функции вида f(x)=msinx или f(x)=mcosx,
После анализа учитель предлагает вниманию учеников готовый алгоритм на плакате (Приложение 3). слайд 8.
-
Построить график основной функции y=sinx или y=cosx (его изображаем пунктирной линией)
-
Осуществить растяжение построенного графика от оси OX с коэффициентом m, если m>1 и осуществить сжатие к оси OX, если 0<m<1с коэффициентом
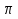 (полученный график изображаем тонкой линией), сохраняя точки пересечения с осью OX
(полученный график изображаем тонкой линией), сохраняя точки пересечения с осью OX -
Если m<0, дополнительно подвергнуть график функции преобразованию симметрии относительно оси OX (полученный график изобразить сплошной жирной линией)
-
Первичное закрепление полученных знаний: слайд 9.
Учитель: «Теперь наша задача, научиться применять полученный алгоритм для решения задач. Вам предлагается поэтапно выполнить задание»
. Организация работы:
-
У доски одновременно работают 2 ученика, остальные ученики работают в тетрадях.
Задания 1 уровня: с помощью полученного алгоритма в системе координат построить поэтапно графики функций 1) № 13.1 (а), 2) № 13.1 (г), затем другие 2 ученика по готовым графикам в той же системе координат строят графики функций 1) № 13.2 (а), 2) № 13.2 (б)
Первый ученик строит график функции № 13.1 (а)
Второй ученик строит график функции № 13.1 (г)
Третий ученик строит график функции № 13.2 (а)
Четвертый ученик строит график функции № 13.2 (б)
-
Самостоятельная фронтальная работа по заданиям учебника с последующей проверкой № 13.3 (а,б), 13.4 (а,б),
Задания 2 уровня для сильных учеников: № 13.10 (а) из задачника
Особое внимание обратить на построение графика функции из этого номера на то, что функция претерпевает разрыв в точке 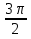
IV. Возвращение к ожидаемым результатам: слайды 10 - 12.
Учитель: Сейчас вам предстоит выполнить небольшой тест, результаты которого покажут, насколько вы усвоили материал сегодняшнего урока и определят задачи следующих уроков (Приложение 4).
Тест
Задание:
Определите, какая графическая модель, соответствует каждой из данных функций:
у =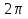 sinx
sinx
у =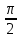 sinx+1
sinx+1
у = - 3sinx
у =3sinx
у = 2sin(x -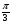 )
)
Буквы, обозначающие графики, запишите рядом с формулой.(тест прилагается)
Если работа выполнена правильно, то вы прочтете имя ученого математика, который содействовал развитию аналитической теории тригонометрических функций.
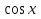
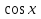
Л Э
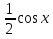
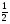
Е Р
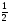
Й
Код:
у =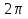 sinx
sinx
у =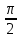 sinx+1
sinx+1
у = - 3sinx
у =3sinx
у = 2sin(x -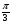 )
)
Э
Й
Л
Е
Р
По окончании работы, решение каждой задачи обсуждается, учащиеся исправляют ошибки, если таковые допущены.
На следующий урок одному из учеников предложить подготовить сообщение о Леонарде Эйлере.
При наличии времени дополнительное задание по карточкам (Приложение 5)
V. Итог урока:
Ребята, как вы считаете, обладает ли алгоритм, который вы составили свойством массовости?
Можно ли его использовать для построения графиков функций y=mtgx (y=mctgx) и других функций?
Мы с вами попробуем это осуществить на одном из последующих уроков.
VI. Домашнее задание: № 13.2 (б, в), 13.3 (в, г), 13.4 (в, г), 13.7 - 13.8 (на выбор по одной букве) слайд 13.
Приложение 1
Практическая работа:
Задание 1. Построить в тетрадях по точкам графики функций y=sin x, y=cos x, заполнить таблицы значений на корточках: 1 вариант для функции y=sin x, а второй - для функции y=cos x и ответить на вопрос: Как изменилось значение функции в каждом из случаев?
x
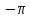
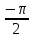
0
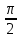
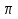
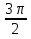
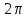
y = 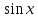
y = 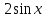
y = 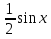
x
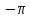
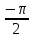
0
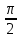
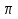
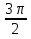
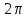
y = 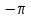
y =2 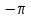
y = 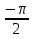
Задание 2. Выясните поведение графиков тригонометрических функций в зависимости от коэффициентов с помощью компьютера. Для этого постройте графики этих функций на компьютере следуя инструкции (Приложение 2), сравните полученные результаты, сделайте вывод, внося соответствующие данные в таблицу:
m
Формула функции
Преобразование графика
2
График функции__________ получается из графика функции ________в результате __________от оси _____
С коэффициентом_______
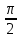
График функции__________ получается из графика функции ________в результате __________от оси _____
С коэффициентом_______
- 1
1. График функции__________ получается из графика функции ________в результате __________от оси _____
с коэффициентом_______
2. подвергнем график функции ________преобразованию ___________относительно оси______
-2
1. График функции__________ получается из графика функции ________в результате __________от оси _____
с коэффициентом_______
2. подвергнем график функции ________преобразованию ___________относительно оси______
- 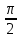
1. График функции__________ получается из графика функции ________в результате __________от оси _____
с коэффициентом_______
2. подвергнем график функции ________преобразованию ___________относительно оси______
Приложение 2
Инструкция по выполнению работы на компьютере с ОС ALT Linux 6.0.0 KDesktop
-
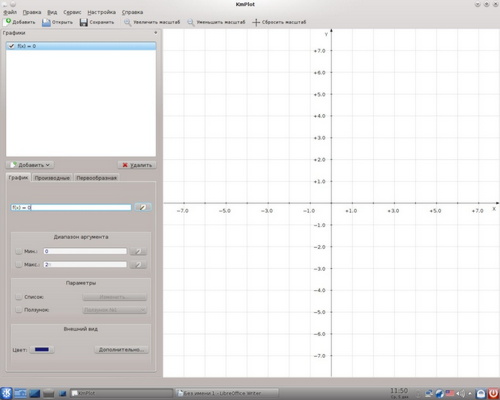
Меню запуска приложений - образование - математика - программа построения графиков (KmPlot)
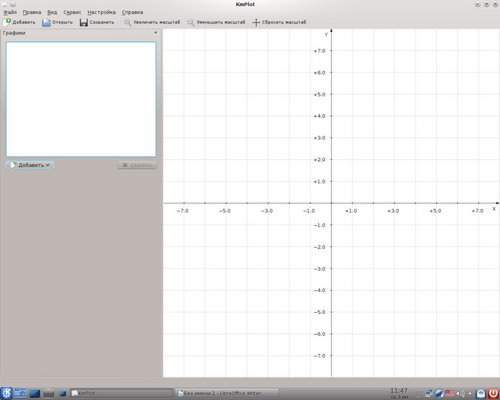
-
графики - добавить
-
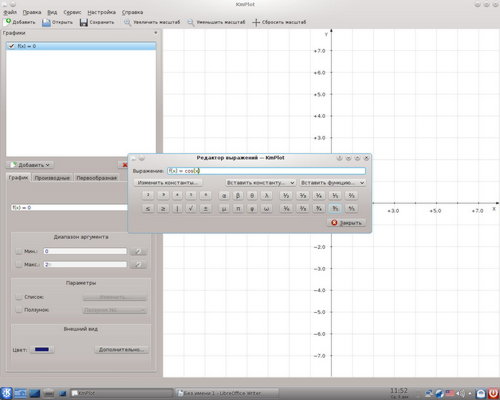
- график в декартовых координатах - редактор выражений - вставить функцию - выбираем cos или sin - переменная в скобках (x) - enter (это основная функция для сравнения)
-
аналогично добавить ещё один график функции f(x)=cosx или f(x)=sinx в этом графике и будем менять коэффициенты чтобы получить графики функций: f(x)=2cosx или f(x)=2sinx
f(x)=0,5cosx или f(x)=0,5sinx
f(x)= -2cosx или f(x)= - 2sinx
f(x)= - 0,5cosx или f(x)= - 0,5sinx
-
Проанализируйте расположение графиков этих функций относительно друг друга, относительно осей координат.
-
Установите связь между аналитической записью функции и преобразованием графика этой функции.
-
Сформулируйте вывод по проделанной работе.
-
Попробуйте составить алгоритм построения графиков функции вида f(x)=msinx или f(x)=mcosx,
Приложение 3
Алгоритм для построения графиков функций вида y= mf(x) или y= mf(x)
-
Построить график основной функции y=sinx или y=cosx (его изображаем пунктирной линией)
-
Осуществить растяжение построенного графика от оси OX с коэффициентом m, если m>1 и осуществить сжатие к оси OX, если 0<m<1 с коэффициентом
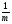 (полученный график изображаем тонкой линией), сохраняя точки пересечения с осью OX
(полученный график изображаем тонкой линией), сохраняя точки пересечения с осью OX
-
Если m<0, дополнительно подвергнуть график функции преобразованию симметрии относительно оси OX (полученный график изобразить сплошной жирной линией)
Приложение 4
Тест
Задание:
Определите, какая графическая модель, соответствует каждой из данных функций:
у =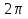 sinx
sinx
у =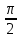 sinx+1
sinx+1
у = - 3sinx
у =3sinx
у = 2sin(x -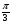 )
)
Буквы, обозначающие графики, запишите рядом с формулой.(тест прилагается)
Если работа выполнена правильно, то вы прочтете имя ученого математика, который содействовал развитию аналитической теории тригонометрических функций.
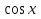
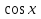
Л Э
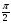
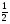
Е Р
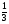
Й
Приложение 5
Самостоятельная работа на 5 вариантов по карточкам.
Вариант 1.
1.Постройте график функции y=3sin(x-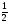 ).
).
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.
Вариант 2.
1.Постройте график функции y= 2cosx+1.
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.
Вариант 3.
1.Постройте график функции y= - 0,5cos(x+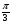 ).
).
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.
Вариант 4.
1.Постройте график функции y=-2,5sinx - 0,5
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.
Вариант 5.
1.Постройте график функции y= - 0,5sin(x-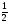 ).
).
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.