Урок по теме Логарифмическая функция

Урок по теме «Логарифмическая функция, ее свойства и график».

Тип урока: урок-лекция.

Учебник: Алгебра и начала анализа: Учеб. Для 10-11 кл. общеобразоват. учреждений / Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др.- 11-е изд.-М.: Просвещение, 2003. - 384 с.

Учебная задача урока: сформировать у школьников представление о логарифмической функции как модели процессов реальной действительности, выявить ее свойства, вид графика.

Диагностируемые цели: в результате урока ученик:

знает определение логарифмической функции, свойства логарифмической функции, основу доказательства свойств, вид графика в зависимости от основания логарифмической функции;

понимает что логарифмическая функция является моделью реальных процессов окружающей действительности, связь между логарифмической и показательной функцией;

умеет доказывать свойства логарифмической функции; применять определение логарифмической функции, свойства логарифмической функции при решении дидактических заданий; выполнять задания на чтение графика логарифмической функции.

Методы обучения: метод эвристической беседы, частично-поисковые, репродуктивный.

Средства обучения: мел, доска, учебник, презентация.

Форма работы: фронтальная.

Структура урока: I. Мотивационно-ориентировочный этап (10 мин);

II. Содержательный этап (30 мин);

III. Рефлексивно-оценочный этап (5 мин).

Перед уроком, в качестве домашнего задания детям задавалось построить график функции: и и записать их свойства.

Ход урока

Мотивационно - ориентировочный этап:

Актуализация:

Учитель вызывает двух учеников к доске: один строит график функции и пишет свойства этой функции, а второй строит график функции и пишет свойства этой функции, а в это время учитель работает фронтально со всем классом.

Учитель: Решим следующие примеры:

№ 1. Вычислите:

Ученики:

Учитель: Сформулируйте определение логарифма.

Ученики: Логарифмом положительного числа b по основанию a, где a>0, a1, называется показатель степени, в которую надо возвести число a, чтобы получить b.

Учитель: Какие особые логарифмы выделяются в математике?

Ученики: Десятичный и натуральный.

Учитель: Какой логарифм называется десятичным? Какой логарифм называется натуральным?

Ученики: Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут lg b.

Натуральным логарифмом числа называют логарифм этого числа по основанию e, где e - иррациональное число, приближенно равное 2,7 и пишут lnb.

№ 2. Вычислите:

1. lg100;2. lg 3. ln1

Ученики: 1. lg100=2; 2. lg1/10=-1; 3. ln1=0

№ 3. Вычислите:

3. .

Ученики:

Учитель: Чем вы пользовались при выполнении задания?

Ученики: Определением логарифма и свойствами логарифмов.

Учитель: Вспомним свойства в общем виде (один ученик выходит и записывает их на доске).

Ученики: пусть :

2. .

Ученики:

Учитель: Чем вы пользовались при выполнении задания?

Ученики: Свойством степени и логарифмов, основным логарифмическим тождеством.

Один ученик выходит и записывает на доске: .

Ученики: .

Учитель: Чем вы пользовались при выполнении задания?

Ученики: свойствами суммы и разности логарифмов.

Один ученик выходит и записывает на доске: ; .

№ 4. Решите неравенство:

Ученики:

Т.к. , то функция убывает на всей области определения функции, тогда:

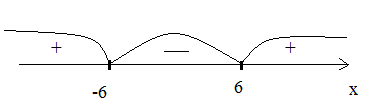
Ответ:

Учитель: Чем вы пользовались при решении данного неравенства?

Ученики: Свойством показательной функции.

Учитель: Сформулируйте определение показательной функции.

Ученики: Показательной функцией называется функция , где - заданное число, .

Учитель: Теперь посмотрим на доску, на ней мы видим график функции , также свойства этой функции. (Ученик рассказывает, как он построил график, и какие выписал свойства, остальные проверяют)

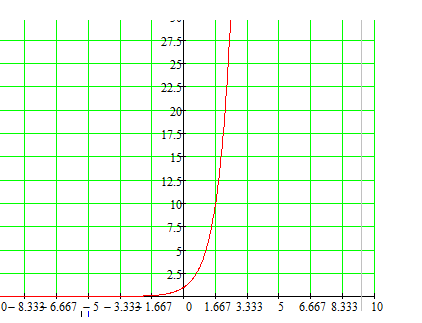
1. D(x): xR

2. E(x): y>0

3.Если x=0,

График пересекает ось ОУ в т. (0;1)

4. y>0 на всей области определения R

5. Функция возрастает на всей области определения

6. Функция общего вида

7. Функция

8. Нет ни наибольшего, ни наименьшего значения.

Теперь посмотрим на график функции и её свойства.

Свойства:

1. D(x): xR

2. E(x): y>0

3.Если x=0,

График пересекает ось ОУ в т. (0;1)

4. y>0 на всей области определения R

5. Функция убывает на всей области определения

6. Функция общего вида

7. Функция

8. Нет ни наибольшего, ни наименьшего значения.

Учитель: В чем различие в свойствах?

Ученики: В виде монотонности.

№ 5. Найдите область определения и множество значений данной функции. Найти функцию, обратную данной, её область определения и множество значений.

Решение:

ОО данной функции:

МЗ данной функции:

Находим обратную функцию:

ОО обратной функции:

МЗ обратной функции:

Учитель: Как связаны области определения и множества значений взаимно обратных функций?

Ученики: Область определения обратной функции совпадает с множеством значений исходной функции, а множество значений обратной функции совпадает с областью определения исходной функции.

Мотивация

Учитель: Итак, изучая понятие степени, мы с вами рассматривали различные функции, связанные с этим понятием, в том числе показательную. Сейчас мы изучаем понятие логарифма. Возникает предположение о существовании соответствующей функции - логарифмической.

Презентация:

Испокон веков целью математической науки было помочь людям узнать больше об окружающем мире, познать его закономерности и тайны. Ряд явлений природы помогает описать именно логарифмическая зависимость. Иначе говоря, математики, пытаясь составить математическую модель того или иного явления, достаточно часто обращаются именно к логарифмической функции. Одним из наиболее наглядных примеров такого обращения является логарифмическая спираль

Уравнение логарифмической спирали в полярной системе координат имеет вид

, где

Переписав уравнение в виде мы увидим, что величина полярного угла пропорциональна логарифму радиус-вектора. Отсюда и происходит название логарифмическая спираль.

Спираль в одну сторону развертывается до бесконечности, а вокруг полюса, напротив, закручивается, стремясь к нему, но не достигая.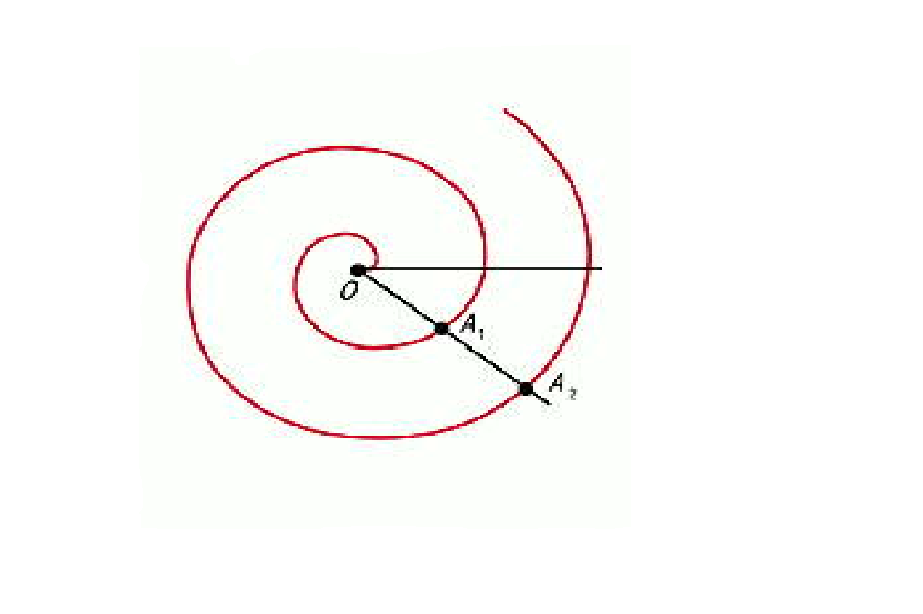

Так почему мы в качестве примера логарифмической зависимости в природе выбрали именно логарифмическую спираль?

Известно, что живые существа обычно растут, сохраняя общее начертание своей формы. При этом чаще всего они растут во всех направлениях - взрослое существо и выше и толще детёныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем рост совершается так, что сохраняется подобие раковины с её первоначальной формой.

А такой рост может совершаться лишь по логарифмической спирали или её некоторым пространственным аналогам. Поэтому раковины многих моллюсков, улиток, а также рога таких млекопитающих, как архары, закручены по логарифмической спирали. Можно сказать, что эта спираль является математическим символом соотношения формы и роста.

Один из наиболее распространенных пауков, эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмическим спиралям. По логарифмическим спиралям закручены и многие галактики, в частности Галактика, которой принадлежит Солнечная система. В подсолнухе семечки расположены по дугам, близким к логарифмической спирали.

Логарифмические линии в природе замечают не только математики, но и художники, например, этот вопрос чрезвычайно волновал Сальвадора Дали.

Его навязчивой идеей стала картина Вермеера «Кружевница», репродукция которой висела в кабинете его отца. Много лет спустя Сальвадор Дали попросил в Лувре разрешение написать копию с этой картины. Затем попросил киномеханика показать на экране репродукцию нарисованной копии. Он объяснил, что, пока не написал эту копию, в сущности, почти ничего не понимал в «Кружевнице», и ему понадобилось размышлять над этим вопросом целое лето, чтобы осознать наконец, что он инстинктивно провёл на холсте строгие логарифмические кривые.

Учитель: Итак, Учебная задача урока: научиться строить график логарифмической функции, изучить её свойства. Запишите тему урока у себя в тетрадях: «Логарифмическая функция, ее свойства и график».

Содержательный этап.

Учитель: Рассмотрим логарифмическую функцию . Какие ограничения накладываются на основание логарифма?

Ученики: Логарифм существует только при а>0 и a1.

Учитель: Попробуйте сформулировать определение логарифмической функции.

Ученики: Логарифмической называется функция , где а - заданное число, a>0, a1.

Учитель: Выберите из предложенных функций логарифмические.

1) 2) 3) 4) ;5)

Ученики: Решение:

1) т. е. логарифм не существует.

2) это не логарифмическая функция, т. к. нет аргумента х.

3) , все условия определения выполняются, это логарифмическая функция.

4)это не логарифмическая функция, т.к. не существует логарифм от нуля.

5) не подходит под определение.

Далее все записи будут вестись в канве - таблицы.

Учитель: Рассмотрим свойства логарифмической функции. Какова область определения логарифмической функции?

Ученики: Множество всех положительных чисел.

Учитель: Почему?

Ученики: По определению логарифма: логарифм существует при .

Учитель: Каково множество значений логарифмической функции?

Ученики: Множество R.

Учитель: Докажем это (дети вместе с учителем доказывают это свойство, фиксируя у себя в канве - таблицы).

Доказательство:

Из определения логарифма следует, что для любого действительного числа b есть такое положительное число , что .

Учитель: Следующее свойство, которое мы рассмотрим - Логарифмическая функция является возрастающей на промежутке x>0, если a>1, и убывающей, если 0<a<1.

Нам надо доказать, что если , то , т.е. , для a>1 и , то , т.е. для 0<a<1.

Ученики: (вместе с учителем).

Доказательство:

1. Пусть a>1. По основному логарифмическому тождеству

( по свойству степени с основанием )

2. Пусть 0<a<1.

По основному логарифмическому тождеству условие можно записать в виде: , получим , так как 0<a<1.

Учитель: Во втором случае основание степени 0<a<1, что происходит со знаком?

Ученики:

Знак изменится на противоположный.

(по свойству степени c основанием 0<a<1)

Учитель:

На практике чаще всего вы будете пользоваться обратной теоремой: если a>1 и , где , то ;

Если 0<a<1 и , где , то

Учитель: Рассмотрим следующее свойство: нули функции.

Если х = 1, чему будет равен логарифм?

Ученики:

Учитель:

Таким образом, график функции всегда пересекает ось Ох в точке (1;0)

Учитель:

Промежутки знакопостоянства.

1. При а > 1, функция принимает положительные значения при x>1, отрицательные при 0<x<1.

2. При.0<a<1, функция принимает положительные значения при 0<x<1, отрицательные при x>1.

Доказательство:

1.Это следует из того, что функция при х = 1, у = 0. Это видно из рисунка:

При а >1 функция является возрастающей. Поэтому на промежутке x > 1 принимает положительные значения. А на промежутке 0<x<1 принимает отрицательные значения.

2. Это следует из того, что функция при х = 1, у = 0. Это видно из рисунка:

При 0<а<1 функция является убывающей. Поэтому на промежутке x > 1 принимает отрицательные значения. А на промежутке 0<x<1 принимает положительные значения.

Учитель: Чётность/нечётность.

Ученики: Является функцией общего вида.

Учитель: Почему?

Ученики: Так как логарифмическая функция определена только при .

Мы рассмотрели все свойства, а теперь рассмотрим одновременно две функции: показательную у и логарифмическую у =

При каких условиях на а рассматривается показательная функция?

Ученики: a>0, a1

Учитель: Какая область определения и какое множество значений у показательной функции? Попробуем сравнить эти данные с областью определения и множеством значений логарифмической функции.у

у =

1. D(x): R

D(x): x>0

2. E(x): x>0

E(x): R

(эта табличка фронтально заполняется всем классом).

Учитель: Какую закономерность вы видите?

Ученики: Область определения показательной функции совпадает с множеством значений логарифмической функции, а множество значений логарифмической функции совпадет с областью определения показательной.

Учитель: Какой предположение на основе этого можно сделать?

Ученики: Это взаимнообратные функции.

Учитель: Мы уже построили графики функций и , теперь давайте построим графики функций и .

График функции будем строить там, где строился график функции , а график функции там, где строился график функции

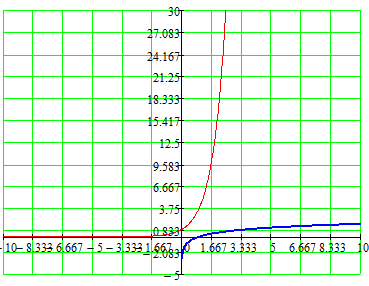
(красный график функции , синий график функции )

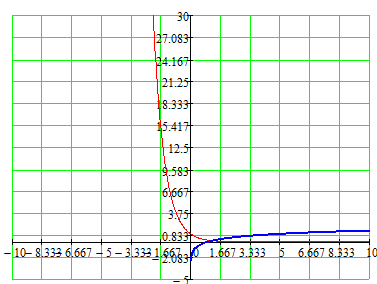
(красный - график функции ; синий - график функции )

Учитель: Относительно какой прямой симметричны графики этих функций?

Ученики: Относительно прямой у = х.

Учитель: Поэтому необязательно строить графики обеих функций. Достаточно построить график одной функции и отобразить его относительно прямой у = х.

Учитель:

Задание1: Построить график функции и по нему найти приближенно

1. , b)

Задание2: по графику функции найти приближенно значения , при которых

График функции

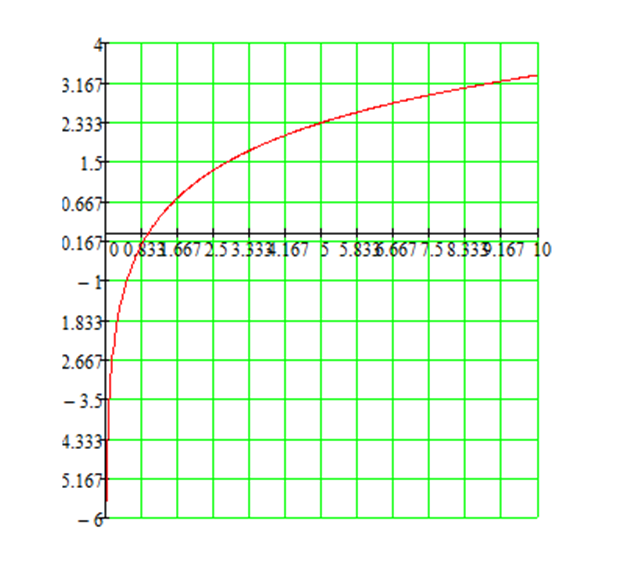
Рефлексивно - оценочный этап.

Учитель: Какова была цель урока?

Ученики: Рассмотреть логарифмическую функцию, её график и свойства.

Учитель: Достигли ли мы ее? Как?

Ученики: Да. Сформулировали определение логарифмической функции, рассмотрели по уже известной схеме все свойства функции, построили её график.

Учитель: Какую связь и между какими функциями мы рассмотрели?

Ученики: Между показательной и логарифмической функциями.

Логарифмическая и показательная функции взаимно обратны.

Учитель: записываем домашнее задание: 1) уметь строить график логарифмической функции, 2) на основе графика формулировать свойства; 3) № 318 (1, 4), №374.

№ 318: задание: сравнить числа:

1. .

Решение: так как , то функция возрастает, а из этого и из того, что следует, что .

4. .

Решение: так как , то функция является убывающей, а из этого и из того, что следует, что . .

№374: Построить график функции и ответить на вопросы: 1) какая из данных функций является возрастающей? Убывающей?2) при каких значениях каждая функция принимает положительные значения? Отрицательные значения? Значения, равные нулю? :

Ответы на вопросы:

1) Возрастающей является функция ; убывающей -

2) при функция принимает положительные значения; при она принимает отрицательные значения; при .

При функция принимает положительные значения; при она принимает отрицательные значения; при .

Логарифмическая функция, её свойства и график.

, a>0, a1

Свойства:

1. Область определения: x>0

2. Множество значений: R

3. Монотонность:

a>1

функция возрастает при х >0

0<a<1

Функция убывает при х>0

если x₁<x₂, то log_ax₁ < log_ax₂

Док-во:

По основному логарифмическому тождеству

( по свойству степени с основанием )

если x₁<x₂, то log_ax₁ > log_ax₂

Док-во:

По основному логарифмическому тождеству:

(по свойству степени с основанием 0<a<1)

3'. Обратная теорема:

если log_ax₁<log_ax₂, то x₁ < x₂

Док-во:

log_ax₁<log_ax₂, тогда ( по свойству степени)

x₁<x₂ (по основному логарифмическому тождеству).

если log_ax₁<log_ax₂, то x₁ > x₂

Док-во:

log_ax₁<log_ax₂, тогда (по свойству степени)

x₁>x₂ (по основному логарифмическому тождеству).

4. Если х = 1, то

График пересекает ось: Ox в т. А (1 ; 0)

5.График не пересекает ось: Oy

6. a > 1

0

0

y<0

x > 1

y>0

0

y>0

x > 1

y<0

Логарифмическая функция, её свойства и график.

, a>0, a1

Свойства:

1. Область определения:

2. Множество значений:

3.Монотонность:

a>1

функция возрастающая

0

Функция убывающая

если x₁<x₂, то log_ax₁ log_ax₂

Док-во:

если x₁<x₂, то log_ax₁ log_ax₂

Док-во:

3'. Обратная теорема:

если log_ax₁<log_ax₂, то x₁ x₂

Док-во:

если log_ax₁<log_ax₂, то x₁ x₂.

Док-во:

4.Если х = 1, то

График пересекает ось: в т. А (1 ; 0 )

5.График не пересекает ось:

6. a > 1

0</</i>

0

y 0

x > 1

y 0

0

y 0

x > 1

y 0