- Учителю
- Конспект урока по геометрии Призма 10кл.
Конспект урока по геометрии Призма 10кл.
1.Бекирова Лутфие Рустемовна
2.Веселовская средняя школа
3.Учитель математики-физики
4.Геометрия
5.10класс
6.Призма.Поверхность призмы,№ урока-46
7.Геометрия,учебник для 10-11классов средней школы/Атанасян.Л.С и др.
Тема: Призма. Поверхность призмы
Математика похожа на многогранный кристалл, каждая из граней которого несет свои возможности серьезного подлинного познания.
П. Александров
Цель урока: ввести понятие призмы
Вид занятия: комбинированный урок.
Задачи урока:
Методы обучения: объяснительно-иллюстративный с использованием информационных технологий (ЭОР, мультимедийная презентация), репродуктивный, метод дифференцированного обучения.
Уровень усвоения информации: 1. - узнавание ранее изученных объектов, свойств ; 2 - выполнение деятельности по образцу, инструкции или под руководством.
Образовательные цели: сформировать представления об основных элементах пространственной геометрической фигуры - призмы, их основных свойствах; сформировать умения распознавать на чертежах, моделях и в реальном мире многогранные геометрические фигуры; способствовать формированию умения организовывать собственную деятельность, выбирать типовые методы и способы выполнения упражнений.
Воспитательные цели: развивать коммуникативные способности; создавать условия для развития скорости восприятия и переработки информации, культуры речи; формировать умение работать в коллективе и команде.
Развивающие цели: способствовать выработке навыков выполнения упражнений на построение прямых и наклонных призм.
Результаты обучения:
-
владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать на чертежах, моделях и в реальном мире геометрические фигуры;
-
сформированность представлений о математике как части мировой культуры и о месте математики в современной цивилизации.
Ход урока
-
Организационный момент (2 мин);
-
Повторение пройденного материала (3 мин).
-
Изучение нового материала (10 мин):
-
Определение призмы;
-
Характеристические свойства призм;
-
Виды призм;
-
Поверхность призмы;
-
Теория о боковой поверхности призмы;
-
Полная поверхность.
-
-
Закрепление, решение задач у доски (15 мин);
-
Самостоятельная работа по тестам (10 мин);
-
Подведение итога урока (2 мин).
Задание на дом (3 мин).1) Знания теории (определения, свойства, формулы).
2) Умение применять теорию к решению задач.
Оборудование:
электронный учебник; компьютер; модели геометрических тел.
Литература.
I. Организационный момент
-
Количество присутствующих;
-
Наличие учебно-письменных принадлежностей;
-
Готовность к уроку;
-
Сообщение темы.
II. Повторение пройденного материала
«Многогранные углы. Многогранник»
-
Дайте определение многогранника.
Ответ: Многогранник - геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней называются ребрами многогранника, а концы ребер - вершинами многогранника.
-
Сформулируйте понятие правильного выпуклого многогранника.
Ответ: Выпуклый многогранник называется правильным, если все его грани - правильные одинаковые многоугольники и все многогранные углы при вершинах равны. Существует 5 видов правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
-
Сформулируйте теорему Эйлера.
Вершины + Грани - Рёбра = 2.
-
Изобразите выпуклый многогранник и укажите грани, ребра и вершины.
Ответ: Куб АВСДА1В1С1Д1, грани: АВСД, …., ребра: АВ, ВС,…, вершины: А, В, С, ….., Д1.
III. Изучение нового материала
Сегодня на уроке мы будем знакомиться еще с одним видом многогранника - это «Призма».
Мозговой штурм: «Ваши ассоциации со словом призма?» (записываются на доске варианты ответов учащихся).
Дается определение призме с математической точки зрения, вводится понятие боковой грани, основанию и ребра призмы. Так же рассматриваем элементы призмы: высота и диагональ.
Призма - это многогранник, две грани которого являются равными многоугольниками, находящимися в параллельных плоскостях, а остальные грани - параллелограммами.
Грани, которые находятся в параллельных плоскостях, называются основаниями призмы, а остальные грани - боковыми гранями призмы.
Рассматривая элементы призмы нельзя не обратить на свойства этой фигуры. Предложить учащимся самим установить свойства призмы и затем обобщить их используя.
При помощи подвижной модели призмы знакомимся с видами призмы, выясняем их отличия друг от друга. Даем определение каждому виду призмы. В зависимости от основания призмы бывают:
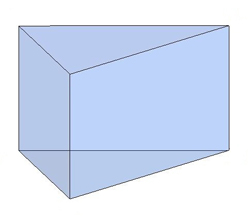
Треугольная
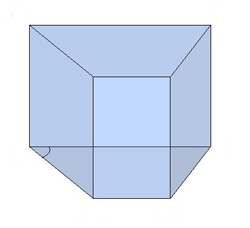
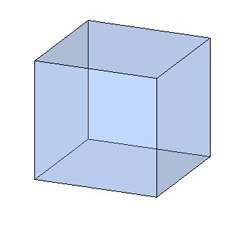
Четырёхугольные
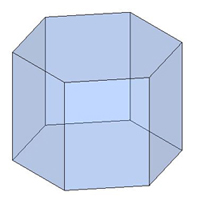
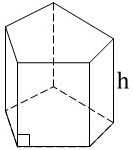
Шестиугольные и др.
Призма с боковыми рёбрами, перпендикулярными её основаниям, называется прямой призмой, как в предыдущих рисунках.
Прямая призма называется правильной, если её основания - правильные многоугольники.
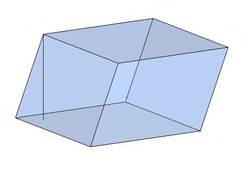
Призма, боковые рёбра которой не перпендикулярны основаниям, называется наклонной призмой.
Расстояние между основаниями призмы называется высотой призмы.
-
Высота прямой призмы совпадает с боковым ребром.
-
Высота наклонной призмы - это перпендикуляр, проведенный между основаниями призмы. Часто перпендикуляр проводят с одной из вершин верхнего основания.
-
Без дополнительных условий невозможно определить, в какую точку проектируется высота наклонной призмы.
Предложить учащимся ответить на вопрос: Что собой представляет развертка призмы. Выслушав ответы, рассмотреть готовый чертеж развертки призмы. Вместе с учащимися знакомимся в формулами, площади боковой поверхности и полной поверхности призмы, так же и для разных видов призм.
Площадь поверхности геометрической фигуры измеряется в квадратных единицах. Очень часто используется в повседневной жизни, в строительстве, на производствах. Например, нужно вам покрасить комнату, зная сколько краски используется на кв. метр, и площади стен комнаты легко можно вычислить, сколько всего вам нужно купить краски.
Различают два вида площадей поверхности тел: Sбок - площадь боковой поверхности тела, и Р - площадь полной поверхности тела, которая равна сумме площадей боковой поверхности и основания тела.
Формула площади поверхности призмы
Площадь боковой поверхности прямой призмы равна периметру основания умноженному на высоту призмы (высота=боковому ребру).
Sбок = ph=pl
р - периметр основания;
h - высота;
l - боковое ребро.
IV. Решение задач
Задача 1
По стороне основания (![]() ) и боковому ребру
(
) и боковому ребру
(![]() ) найдите полную
поверхность правильной призмы.
) найдите полную
поверхность правильной призмы.
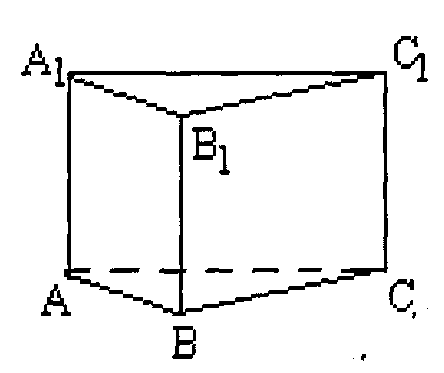
Дано:
![]() - правильная
треугольная призма.
- правильная
треугольная призма.
![]() ;
;
![]() .
.
Найти: ![]()
Решение:
![]()
Боковая поверхность призмы равна: ![]() ;
; ![]() , тогда
, тогда ![]() .
.
Ответ: ![]() .
.
Задача 2
Боковая поверхность правильной четырехугольной призмы 32 м2, а полная поверхность - 40 м2. Найдите высоту.
Дано:
![]() - правильная
треугольная призма.
- правильная
треугольная призма.
![]() м2;
м2; ![]() м2.
м2.
Найти: ![]()
Решение:
![]() ,
отсюда имеем:
,
отсюда имеем:
![]() м2
м2
Так как в основании находится квадрат, то сторона
квадрата равна: ![]() , то
, то
![]() м.
м.
Ответ: 4 м.
V. Самостоятельная работа по тестам
1 вариант
-
Сторона основания правильной шестиугольной призмы равна 4 см, а большая диагональ призмы образует с основанием угол, равный 60°. Найдите площадь полной поверхности призмы.
а) 212 см2; б) ![]() см2; в)
288 см2; г)
см2; в)
288 см2; г) ![]() см2.
см2.
-
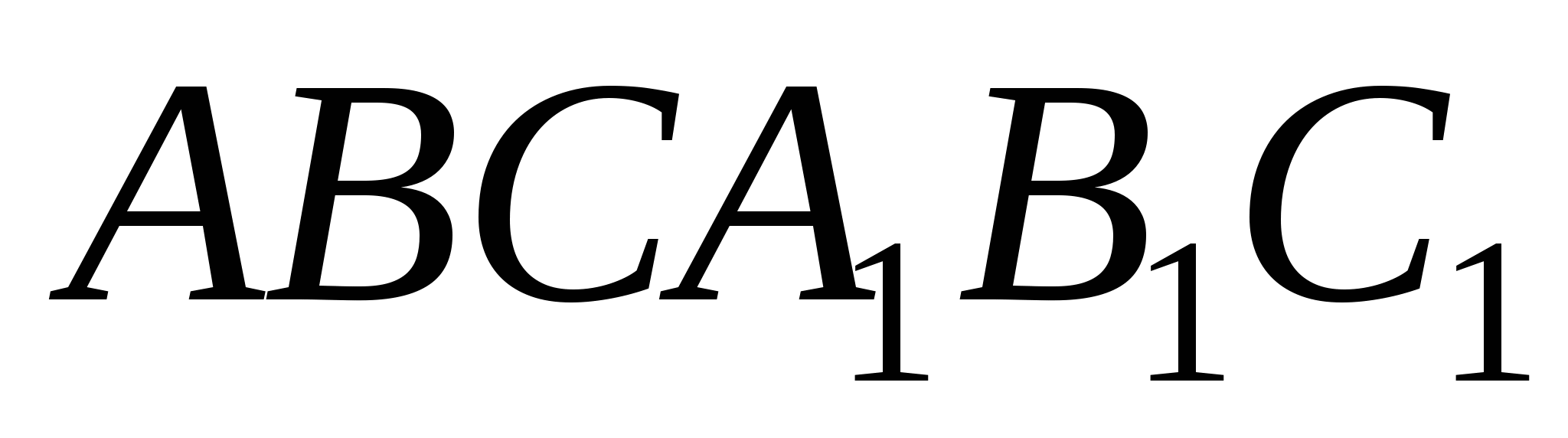 - правильная
треугольная призма. Через ребро
- правильная
треугольная призма. Через ребро 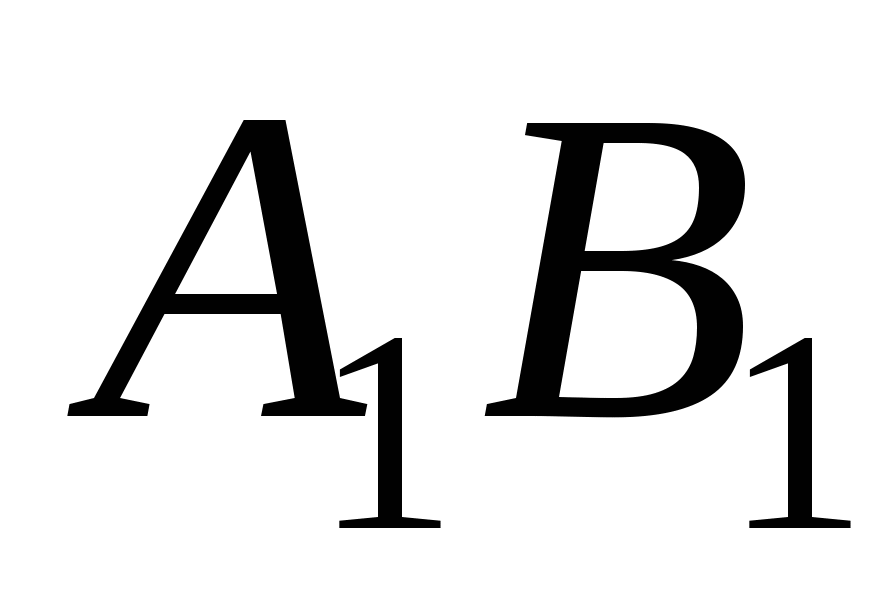 и точку
и точку 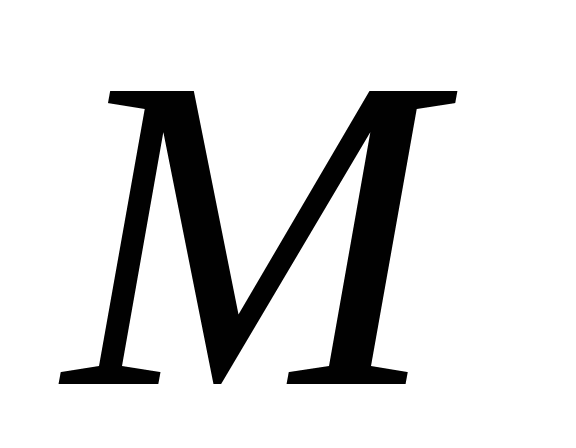 - середину
- середину
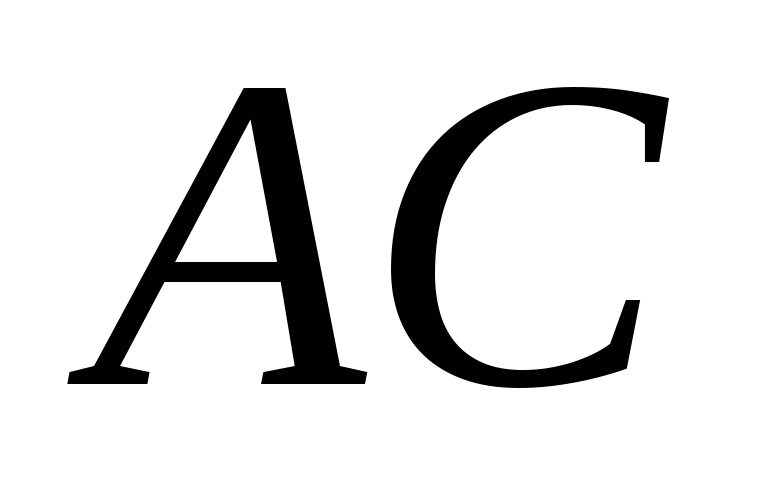 проведено
сечение, площадь которого равна
проведено
сечение, площадь которого равна 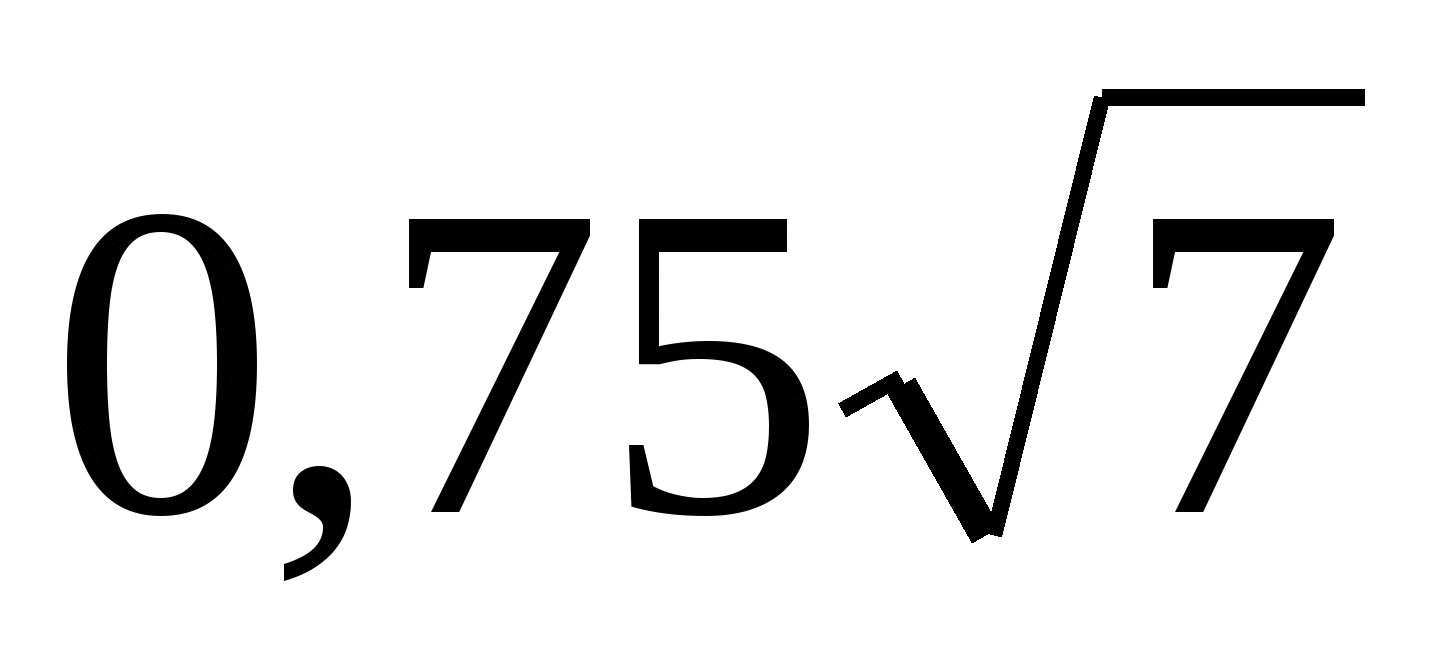 см2. Найдите
высоту призмы, если сторона ее основания равна 2 см.
см2. Найдите
высоту призмы, если сторона ее основания равна 2 см.
а) ![]() см2; б)
1,5 см2; в) 1 см2; г)
см2; б)
1,5 см2; в) 1 см2; г) ![]() см2.
см2.
-
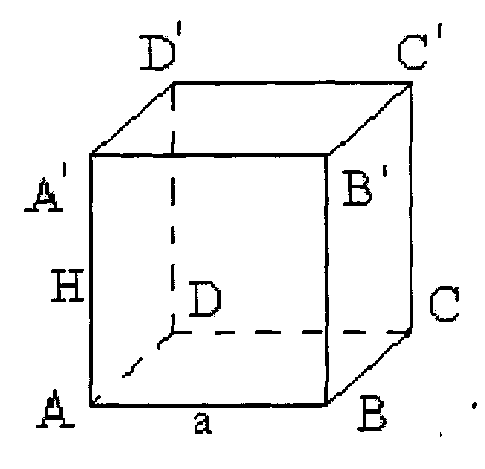
Площадь диагонального сечения куба равна
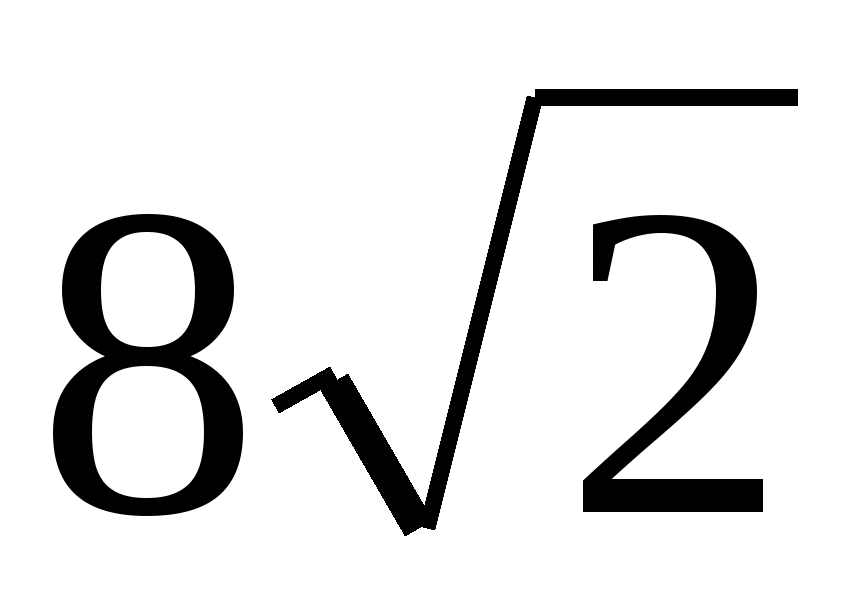 см2.
Найдите площадь поверхности куба.
см2.
Найдите площадь поверхности куба.
а) ![]() см2; б)
см2; б)
![]() см2; в)
см2; в)
![]() см2; г) 48
см2.
см2; г) 48
см2.
-
Стороны основания прямого параллелепипеда равны 1 см и 3 см, a sin угла между ними равен
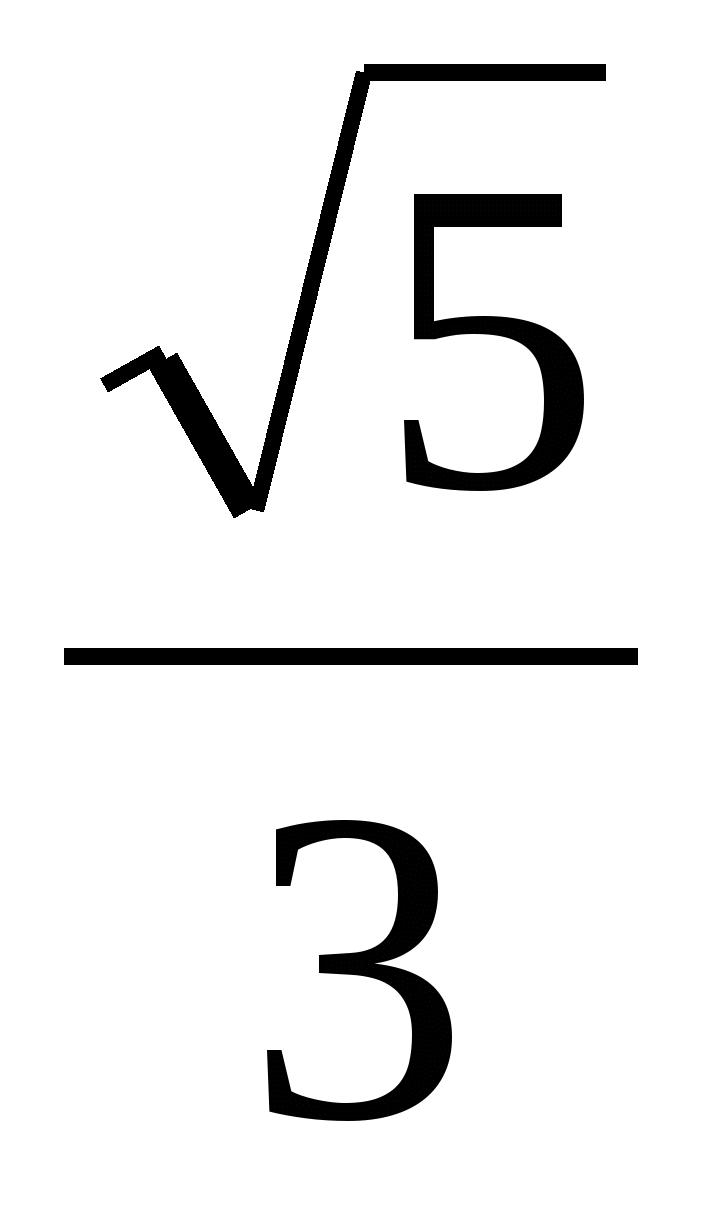 . Найдите угол,
который образует большая диагональ параллелепипеда с
основанием, если боковое ребро параллелепипеда равно
. Найдите угол,
который образует большая диагональ параллелепипеда с
основанием, если боковое ребро параллелепипеда равно
 см.
см.
а) ![]() ; б)
; б) ![]() ; в) 45°; г) 30°.
; в) 45°; г) 30°.
Критерии оценок
На оценку: «5» - 3 задания;
«4» - 2 задания;
«3» - 1 задание по выбору.
2 вариант
-
Сторона основания правильной шестиугольной призмы равна 6 см, а большая диагональ призмы образует с основанием угол, равный 30°. Найдите площадь полной поверхности призмы.
а) ![]() см2; б)
288 см2; в)
см2; б)
288 см2; в) ![]() см2; г) 272 см2.
см2; г) 272 см2.
-
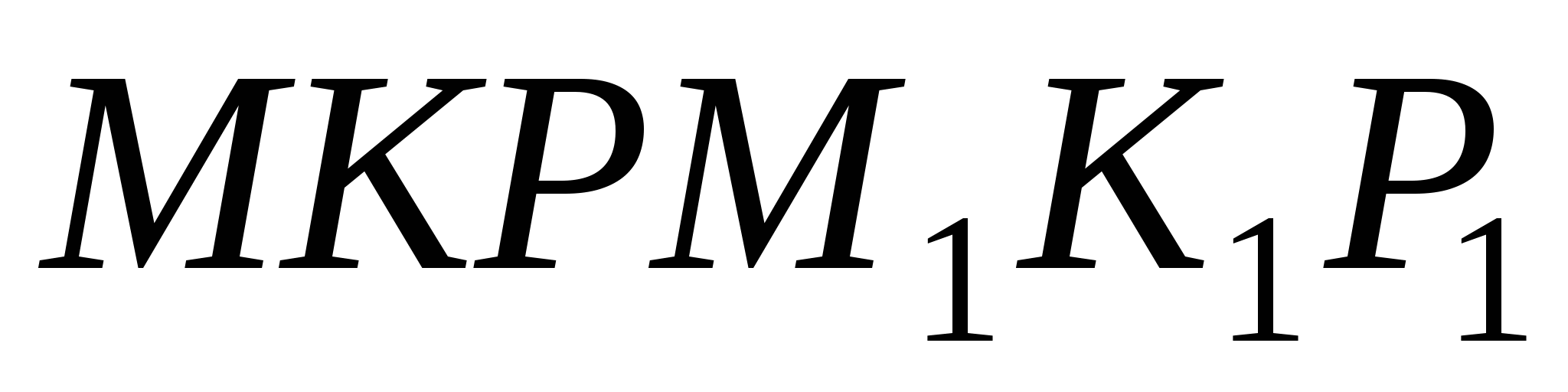 - правильная
треугольная призма, сторона основания которой 4 см. Найдите
площадь сечения призмы плоскостью, проходящей через точки
- правильная
треугольная призма, сторона основания которой 4 см. Найдите
площадь сечения призмы плоскостью, проходящей через точки
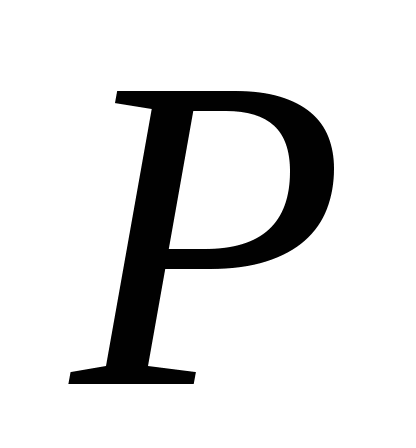 ,
,  и
и 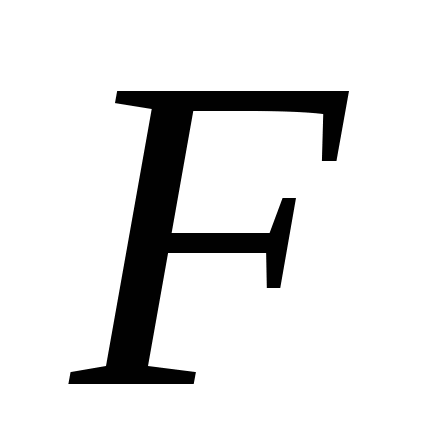 , где
, где и
и 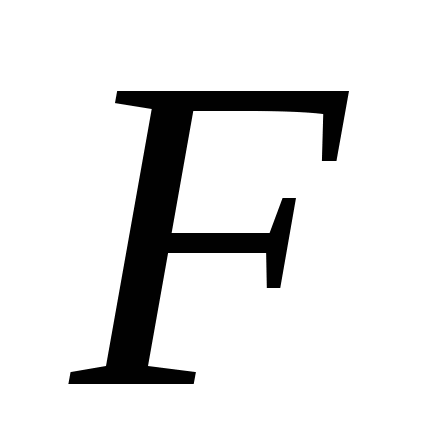 - середины ребер
- середины ребер
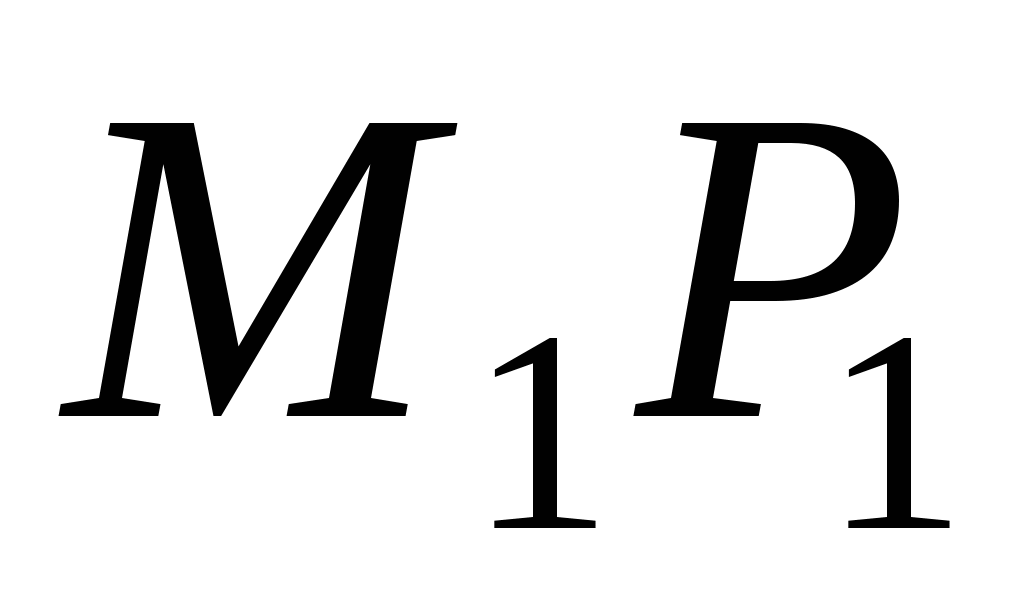 и
и 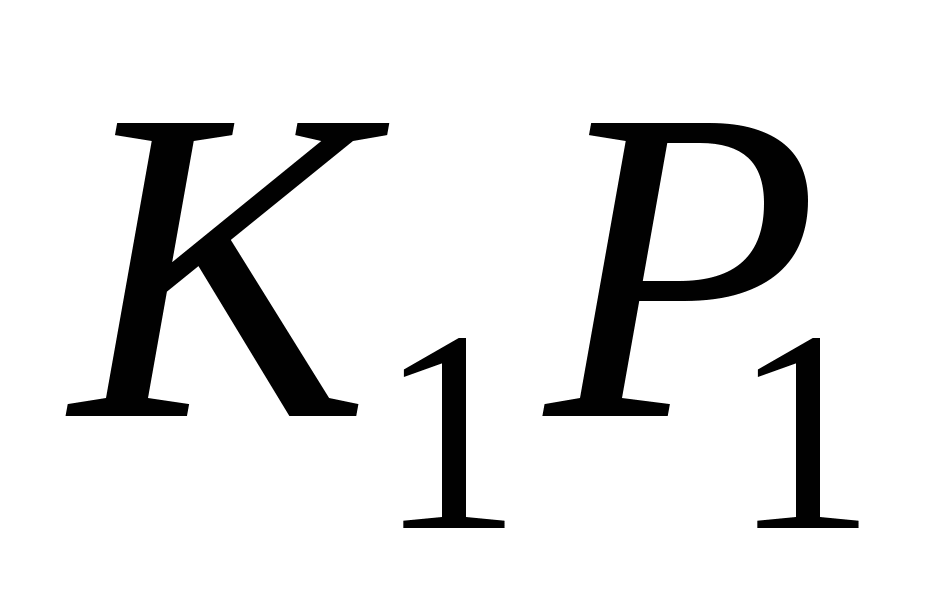 , а боковое ребро
равно 3 см.
, а боковое ребро
равно 3 см.
а) ![]() см2; б) 3
см2; в) 4 см2; г)
см2; б) 3
см2; в) 4 см2; г) ![]() см2.
см2.
-
Площадь поверхности куба равна
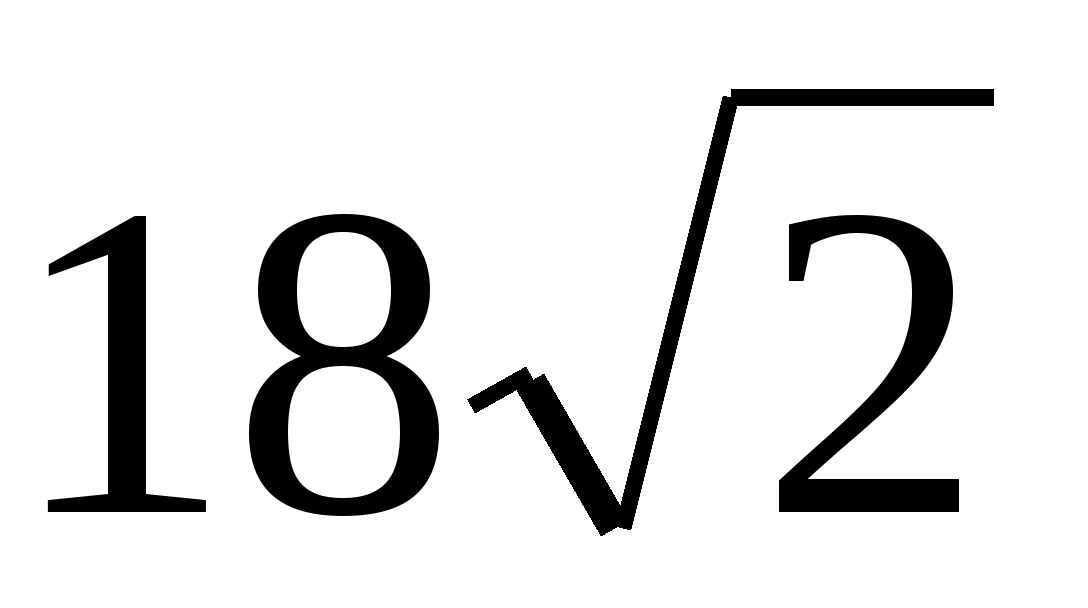 см2.
Найдите площадь диагонального сечения этого куба.
см2.
Найдите площадь диагонального сечения этого куба.
а) ![]() см2; б) 6
см2; в)
см2; б) 6
см2; в) ![]() см2; г) 8 см2.
см2; г) 8 см2.
-
Стороны основания прямого параллелепипеда равны 2 см и 4 см, a sin угла между ними равен
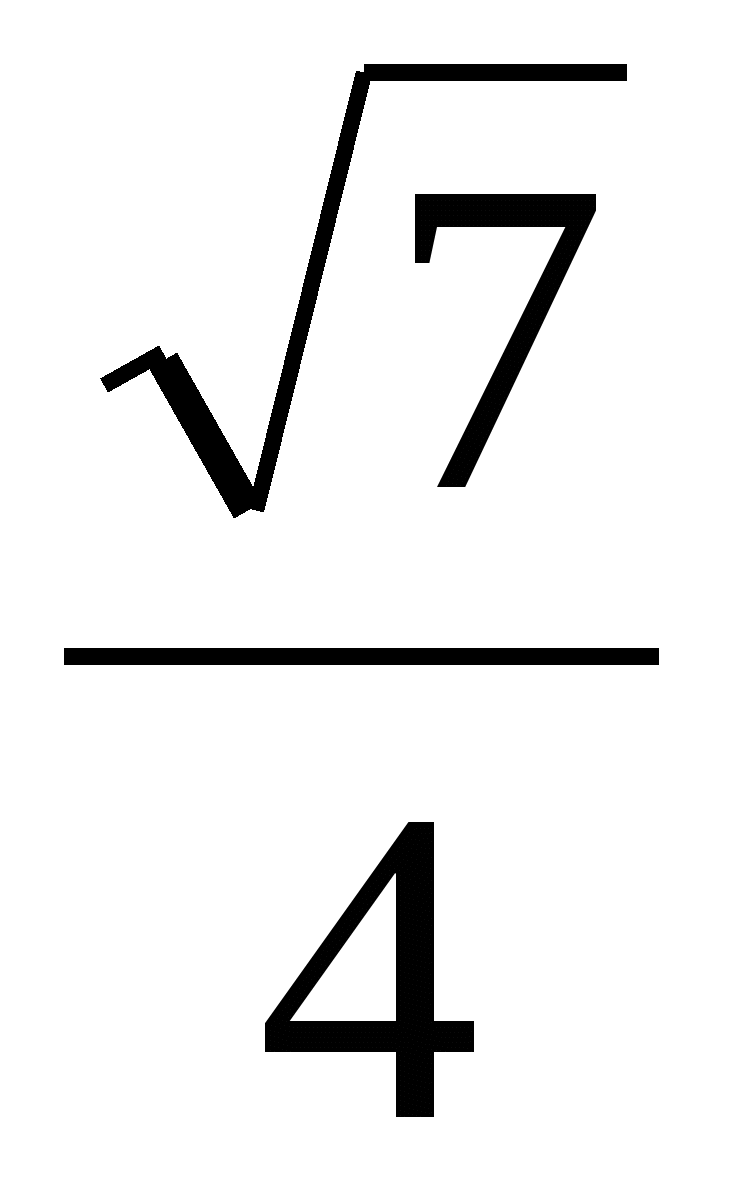 . Найдите угол,
который образует меньшая диагональ параллелепипеда с
основанием, если ее длина
. Найдите угол,
который образует меньшая диагональ параллелепипеда с
основанием, если ее длина 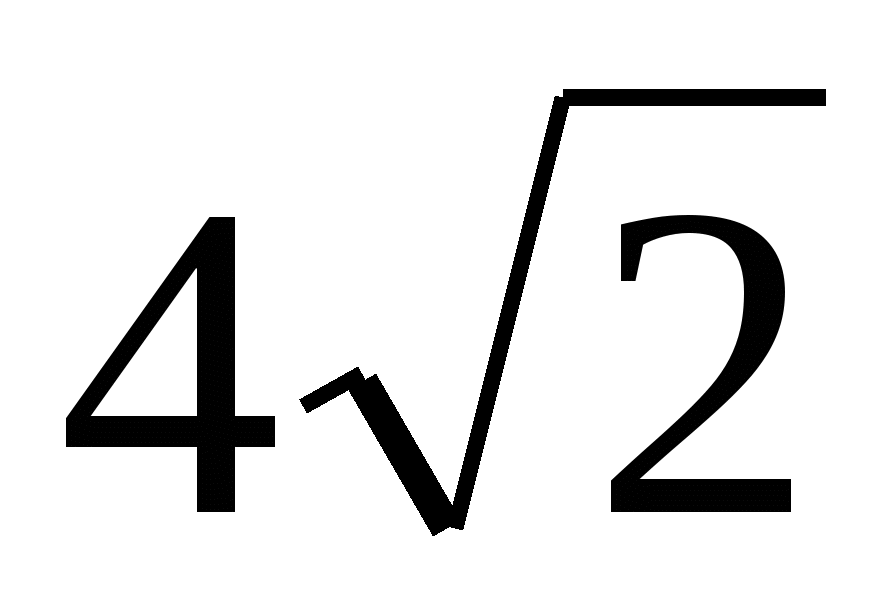 см.
см.
а) ![]() ; б) 30°; в) 60°; г)
45°.
; б) 30°; в) 60°; г)
45°.
Критерии оценок
На оценку: «5» - 3 задания;
«4» - 2 задания;
«3» - 1 задание по выбору.
Контроль знаний
Ответить на вопросы:
-
Чем отличается правильная призма от прямой?
-
Что можно сказать об основаниях любой призмы?
-
Как расположены боковые грани прямой призмы относительно основания?
-
Две смежные боковые грани призмы перпендикулярны основанию. Установить, прямой или наклонной является призма.
-
Укажите различие в понятиях: правильная призма, наклонная призма и прямая призма.
-
Чему равна полная поверхность наклонной призмы?
VI. Подведение итога урока
-
Комментирование оценок;
-
Задание на дом. Инструктаж по домашнему заданию:
. стр. 67 № 225, 227.
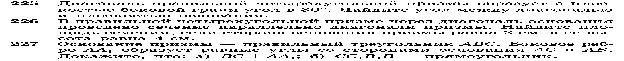
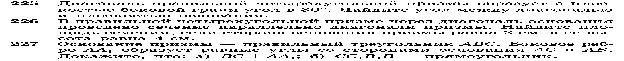


Список использованных источников
-
Геометрия. Учебник для 10-11классов [Текст] Учебник для 10 - 11 классов средней школы / Атанасян Л.С. [и др.] : Просвещение, 2014. - 255 с.
-
ГДЗ - готовое домашние задание по геометрии за 10-11 класс к учебнику Атанасяна онлайн [Электронный ресурс] // Режим доступа: ggddzz.ru/reshebnik/gdz-po-geometrii-10-11-klass-atanasjan/list/218/
3. Образовательный портал «Инфоурок» / Тесты по геометрии 10-11 класс [Электронный ресурс] // Режим доступа: infourok.ru/konkurs?dwldurl=http%3A%2F%2Ffs01.infourok.ru%2Fuploads%2F120855060428.doc
4.Социальная сеть работников образования [Электронный ресурс] // Режим доступа: nsportal.ru/shkola/geometriya/library/2013/02/16/test-prizma</</u>