- Учителю
- Авторлық бағдарлама тақырыбы: « Ұлттық бірыңғай тестілеуде кездесетін есептерді шығару»
Авторлық бағдарлама тақырыбы: « Ұлттық бірыңғай тестілеуде кездесетін есептерді шығару»
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ
МИНИСТРЛІГІ
ҚЫЗЫЛОРДА ОБЛЫСЫ,ҚАЗАЛЫ АУДАНЫ,ӘЙТЕКЕ БИ КЕНТІ
№266 МЕКТЕП-ЛИЦЕЙ
Авторлық бағдарлама тақырыбы:
« Ұлттық бірыңғай тестілеуде кездесетін есептерді шығару»
( 11 сыныпқа арналған бағдарлама )
Құрастырушы:Ескалиева Гулнур Бакытбековна
(математика пәні мұғалімі)
2015-2016 оқу жылы
«Бекітемін»: «Келісілді»: Қаралды және
Мектеп-лицей Бейінді оқыту жөніндегі бекітілді:
директоры: орынбасары: Педагоикалық кеңесте
_______ Л.Р.Ізбасар _______ Б.Ж.Райсова Хаттама №1
«28» тамыз 2015 ж
БАҒДАРЛЫ ОҚЫТУ КУРСЫНЫҢ
БАҒДАРЛАМАСЫ
Таңдау курсының тақырыбы:
« Ұлттық бірыңғай тестілеуде кездесетін есептерді шығару»
( 11 сыныпқа арналған бағдарлама )
Бағдары:қоғамдық - гуманитарлық
Құрастырушы:Г.Есқалиева
2015 - 2016 оқу жылы
Әйтеке би кенті
« Ұлттық бірыңғай тестілеуде кездесетін есептерді шығару»
11-сынып
Таңдау курсының түсінік хаты
Жоғары сынып оқушыларын таңдау сабақтарымен қамтамасыз ету үшін « Ұлттық бірыңғай тестілеуде кездесетін есептерді шығару»
атты курсы құрылды.Ұсынылып отырған курс жоғары сынып оқушыларының кәсіби дайындық міндеттерін жүзеге асыруға көмектеседі.Курс 34 сағатқа есептеліп,11-сынып оқушыларына арналған.
Бұл курс математикаға бейімі бар оқушының қызығушылығын,сұранысын стандартты емес есептер шешу әдістерінде танымдық қажеттіліктерін қанағаттандыруға, негізгі бағдарламалық материалды жоғары деңгейде меңгеруге бағытталған. Басқа жағынан алғанда,бұл курс 11-сынып оқушылары үшін жоғарғы оқу орнына дайындық болып табылады.
Курстың мақсаты: -оқушылардың ойлау қабілеті қиындыгы жогары логиқалық есептер арқылы дамыту;
-жоғары математика теорияларын оқып үйрене отырып есептер шығаруға үйрету;
-оқушылардың шығармашылық ізденістерін дамыту.
Курс міндеттері:
-
Ұлттық бірыңғай тестілеуде кездесетін есептерді шығару, білімдерін жүйелеу және тереңдету.
-
Әртүрлі әдіс-тәсілдерді пайдалана отырып,оқушылардың есеп шығаруға практикалық дағдыларын дамытуға және қалыптастыруға жағдай жасау.
-
Шығармашылық және логикалық ойлауларын дамыту.
-
Білімін пайдалану және өздігінен білім алу дағдыларын дамыту.
-
Оқушының математикалық мәдениетін көтеру.
Курсты меңгеруге қойылатын талаптар:
Курс оқу нәтижесінде оқушылар келесі білім, білік әдістерді меңгереді
- Нақтыны тану әдісі,бейнелеу математика туралы көзқарас-
тарын қалыптастырады;
- Саралау , салыстыру , теңестіру , жүйелеу , қорытындылау-
ды үйренеді;
- Математикалық әдебиеттермен өздігінен жұмыс жасай
алады;
-
Стандарттық емес теңдеулер шешудің негізгі әдістерін біле-
ді, теңдеу шешу әдістерінің теориялық негізін түсінеді;
- Әртүрлі әдістермен стандартты емес теңдеулерді шеше алады
- Пікір таласқа қатысып,өз қызметінің нәтижесін болжай
алады;
-
Өз қызметіне анализ жасап, жұмыс нәтижесін бағалай алады.
Күтілетін нәтиже:
-
Оқушылардың математикалық білімінің жоғарылауы;
-
Логикалық ойлау қабілетінің дамуы;
-
Есептер шығару арқылы шығармашылық жұмыстану деңгейінің жоғарылауы;
Білуі керек:
-
Әртүрлі ақпарат көздерімен жұмыс жасауға;
-
Қорытынды ой жасау және нәтижені сараптауы;
-
Пікір таласқа қатысу , өз қызметінің нәтижесін көре білуге;
-
Параметрлері берілген теңдеулерді әртүрлі әдістермен шешуге;
-
Есеп шығарудың ұтымды жолын таңдауды;
-
Нәтижесін график арқылы көрсетуді.
Пәнаралық байланыс: физика,геометрия,химия,информатика
Уақыт көлемі: жалпы сағат саны-34,аптасына 1 сағат
Курсты ұйымдастыру формасы: тақырыптық есептер шығару
Курсты оқытуды аяқтау формасы: сынақ(зачет) тапсыру
Оқушылардың оқу жетістіктерін бағалау жүйесі:
Дихатомиялық жүйе:
«меңгерді» немесе «меңгермеді». Өткізілетін орны: III этаж,«Д» блогы,11«Г» кл
Ұсынылатын әдебиеттер:
Мұғалімдер үшін: 1.Мектеп оқулықтары,А.Әбілқасымова
11-сынып.Алгебра және анализ бастамалары
2.И.П.Рустюмова «Пособие для подготовки к
единому национальному тестированию по
математике»,Алматы-2009
3.«Физика және математика» ғылыми-әдістеме-
лік журналы
4.«Математика» ғылыми-әдістемелік журналы
Оқушылар үшін: 1.Оқулықтар,8-сынып және 11-сыныптар үшін
Алгебра,Геометрия
2.«Алгорифм», «Репетитор» журналдары
3.Математика «Оқушы анықтамалығы»
4.Исмайл Акиол .Алматы 2006ж.«Шың»
№1,2 ;оқулық-тест
5.«Математика» талапкерлерге арналған тест
2000-2015 ж.ж.
6.Талапкер авт. Н:В:Егорина.
«Келешек-2030»баспасы,2011жыл.
Курстың оқу-тақырыптық жоспары
Р\с
Тақырыптыр мазмұны
Сағат саны
Ұйымдастыру формасы
Уақыты
1
Функция
2
Теориялық,
практикалық
2
Натурал көрсеткішті дәреже
2
Теориялық,
практикалық
3
Арифметикалық прогрессия
2
Теориялық,
Практикалық
4
Геометриялық прогрессия.
2
Теориялық,
Практикалық
5
Тригонометриялық өрнектер және оларды түрлендіру
2
Теориялық,
Практикалық
6
Тригонометриялық теңдеулер
3
Теориялық,
Практикалық
7
Логарифмдік функциялар
3
Теориялық,
практикалық
8
Көрсеткіштік функциялар
3
Теориялық,
практикалық
9
Туынды және оның қолданылуы.
3
Теориялық,
практикалық
10
Алғашқы функция
3
Практикалық
11
Қарапайым геометриялық фигуралар
2
Теориялық,
Практикалық
12
Векторлар
2
Теориялық,
Практикалық
13
Көпжақтар
2
Теориялық,
практикалық
14
Айналу денелері
2
Теориялық,
практикалық
15
Тест тапсырмалары
1
Сынақ
Сабақ: № 1
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Функция
Сабақтың мақсаты:
а) Білімділік: Оқушыларды функцияның шығу тарихымен, практикада пайдалануымен таныстыру;
ә) Дамытушылық: Ойлау, есептеу ережені есте сақтау қабілеттерін дамыту. Оқулықтан тыс ақпаратты пайдалану;
б) Тәрбиелік: Оқушылардың топтық жұмысы арқылы өз ойларын ашық айтып, жолдастарының ойын тыңдап, жауабын бағалауға, ұйымшылдық қасиеттерге тәрбиелеу.
Сабақтың түрі: зерттеулік жұмыстар, практикум сабақ
Сабақтың әдісі: Сұрақ - жауап, топтастыру
Сабақтың көрнекілігі: оқулық.Математика.ҰБТ-ға дайындаламыз
Пәнаралық байланыс: қоғамтану, геометрия, физика т.б.
Сабақ барысы:
І. Ұйымдастыру кезеңі:
Оқушылармен сәлемдесу;Оқушыларды түгелдеу;Назарларын сабаққа аудару.
ІІ. Өткен материалдарды еске түсіру:
1.Функция ұғымын қалай түсінесіңдер?
2. Мысал келтір
3. Функция графигін қалай саламыз?
Анықтама: Х жиынындағы х - тің әрбір мәніне У жиынының нақты бір у мәнін сәйкес қоятын ереже немесе заңдылық функция деп аталады. Латынша (function - « аяқтау, орындау » )
Былай белгіленеді: у= f(х), мұндағы х - тәуелсіз айнымалы немесе функцияның аргументі, у - тәуелді айнымалы немесе функция, f g... - ереже немесе заңдылық
Мысалы: у= 2х+3
Функция тиянақты мән қабылдайтын тәуелсіз айнымалының нақты мәндер жиынын функцияның анықталу облысы (Д), ал анықталу облысынан алынған әрбір тәуелсіз айнымалыға сәйкес табылған функцияның мәндерін оның мәндер жиыны (Е) деп атаймыз. Мысалы: у= 2х2-3х-17, Д(у) = R , себебі көпмүше т.б.
III.Тапсырмалар:
Оқулықтан 3- модуль есептерін шығару
IҮ. Тарихи мәліметтер.
1. Функцияның алғашқы анықтамасын Декарт «Геометрия» атты еңбегінде ұсынды.
2. «х-тен функция» терминін алғаш Г.В.Лейбниц пен шәкірті И.Бернулли қолданды.
3. 1698 жылдан бастап Лейбниц айнымалы және «константа» ( тұрақты ) терминдерін енгізді.
4. 1718 жылы швейцариялық матеметик И.Бернулли функцияға дәлірек анықтама берді:
«Айнымалы шаманың функциясы деп осы айнымалы мен тұрақтыдан қандай да бір тәсілмен құрылған шаманы айтады».
5. Қазігі кезде қабылданған функцияның белгіленуін Л.Эйлер енгізген.
Білгіңіз келсе...
Рене Декарт ( 1596-1650 ) - француздың ұлы философы, математигі. Аналитикалық гоеметрияны жасаушылардың бірі. Айнымалы шамалар ұғымын енгізген. Латынша аты - Картезий. Еңбектері «Гоеметрия», «Рассуждение о методе».
Леонард Эйлер (1707-1783 ) - 18 ғасырдың көрнекті математигі, швейцарияда туған. Эйлердің зор ғылыми мұралары математикалық анализге, гоеметрияға, сандар теориясына, механикаға және басқа да математиканың қосымшаларына қатысты алған тамаша нәтижелерден тұрады.
Лейбниц Годфрид Фридрих (1646-1716 ) - немістің ұлы ғалымы. Философ, математик, физик, юрист, тіл зерттеушісі. Математикалық анализді құрушы. Үлкен математикалық мектептің негізін салушы. Лейбниц идеялары математикалық логиканың дамуына зор ықпал жасады.
Ү. Сабақты қорытындылау
«Insert» кестесін толтырамыз да қорытынды жасаймыз.
Білгім келеді
ҮІ. Үйге тапсырма:
№10, 12 есептер
Реферат: «Леонард Эйлер»
Сабақ: № 2
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Функция
Сабақтың мақсаты:
а) Білімділік: Оқушыларды функцияның шығу тарихымен, практикада пайдалануымен таныстыру;
ә) Дамытушылық: Ойлау, есептеу ережені есте сақтау қабілеттерін дамыту. Оқулықтан тыс ақпаратты пайдалану;
б) Тәрбиелік: Оқушылардың топтық жұмысы арқылы өз ойларын ашық айтып, жолдастарының ойын тыңдап, жауабын бағалауға, ұйымшылдық қасиеттерге тәрбиелеу.
Сабақтың түрі: зерттеулік жұмыстар, практикум сабақ
Сабақтың әдісі: Сұрақ - жауап, топтастыру
Сабақтың көрнекілігі: оқулық.Математика.ҰБТ-ға дайындаламыз
Пәнаралық байланыс: қоғамтану, геометрия, физика т.б.
Сабақ барысы:
І. Ұйымдастыру кезеңі:
Оқушылармен сәлемдесу;Оқушыларды түгелдеу;Назарларын сабаққа аудару.
ІІ. Өткен материалдарды еске түсіру:
1.Функция ұғымын қалай түсінесіңдер?
2. Мысал келтір
3. Функция графигін қалай саламыз?
Анықтама: Х жиынындағы х - тің әрбір мәніне У жиынының нақты бір у мәнін сәйкес қоятын ереже немесе заңдылық функция деп аталады. Латынша (function - « аяқтау, орындау » )
Былай белгіленеді: у= f(х), мұндағы х - тәуелсіз айнымалы немесе функцияның аргументі, у - тәуелді айнымалы немесе функция, f g... - ереже немесе заңдылық
Мысалы: у= 2х+3
Функция тиянақты мән қабылдайтын тәуелсіз айнымалының нақты мәндер жиынын функцияның анықталу облысы (Д), ал анықталу облысынан алынған әрбір тәуелсіз айнымалыға сәйкес табылған функцияның мәндерін оның мәндер жиыны (Е) деп атаймыз. Мысалы: у= 2х2-3х-17, Д(у) = R , себебі көпмүше т.б.
3.Есеп шығару
-
Мын функциялардың қайсысы сызықтық функцияға жатады. Жауабы: у=3х+4
-
Сөйлемді толықтырыңыз. «Сызықтық функцияның анықталу облысы ...тұрады».
Жауабы: барлық нақты сандар
-
Сөйлемді толықтырыңыз. «Сызықтық функция графигі ... болады».
-
Жауабы: түзу сызық
-
Сызықтық функцияның графигін салу үшін графиктің неше нүктесінің координаталарын тауып, оларды координаталық жазықтықта белгілеуге болады. Жауабы: екі
-
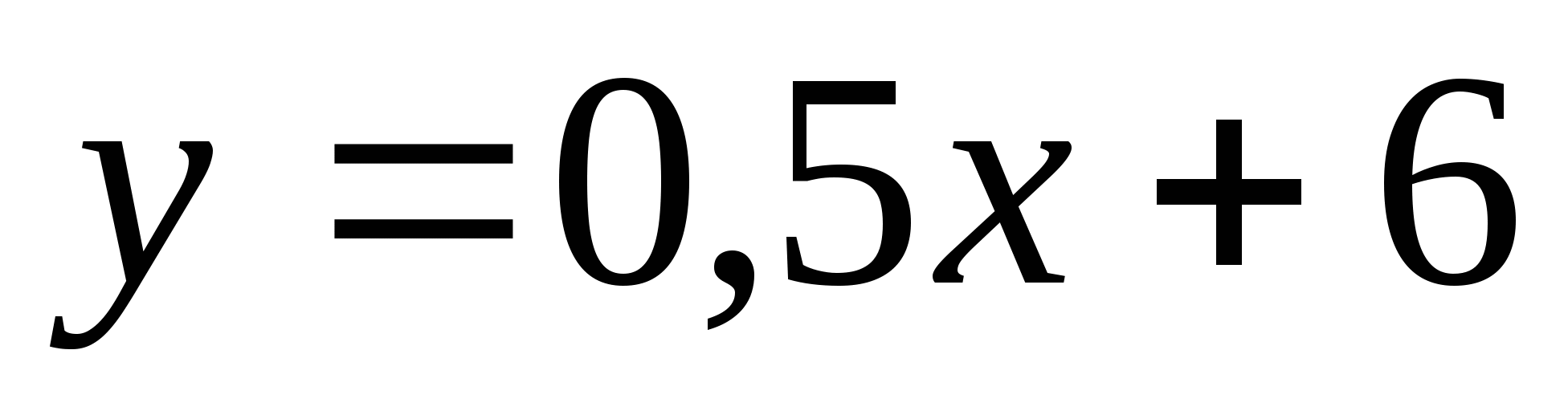 функциясының
функциясының
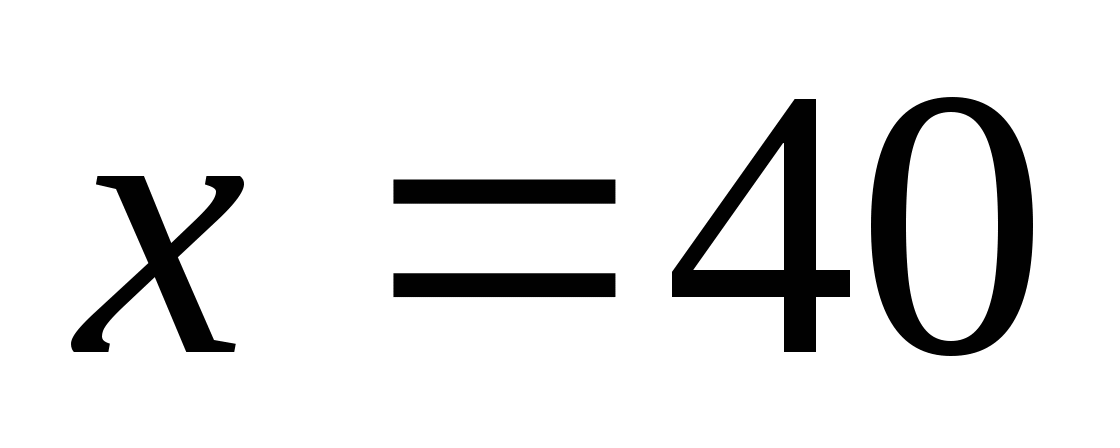 болғандағы
болғандағы 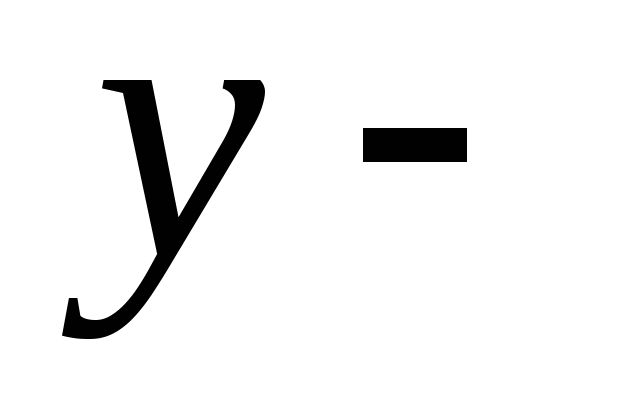 тің сәйкес мәнін тапбыңыз. Жауабы: 26
тің сәйкес мәнін тапбыңыз. Жауабы: 26
-
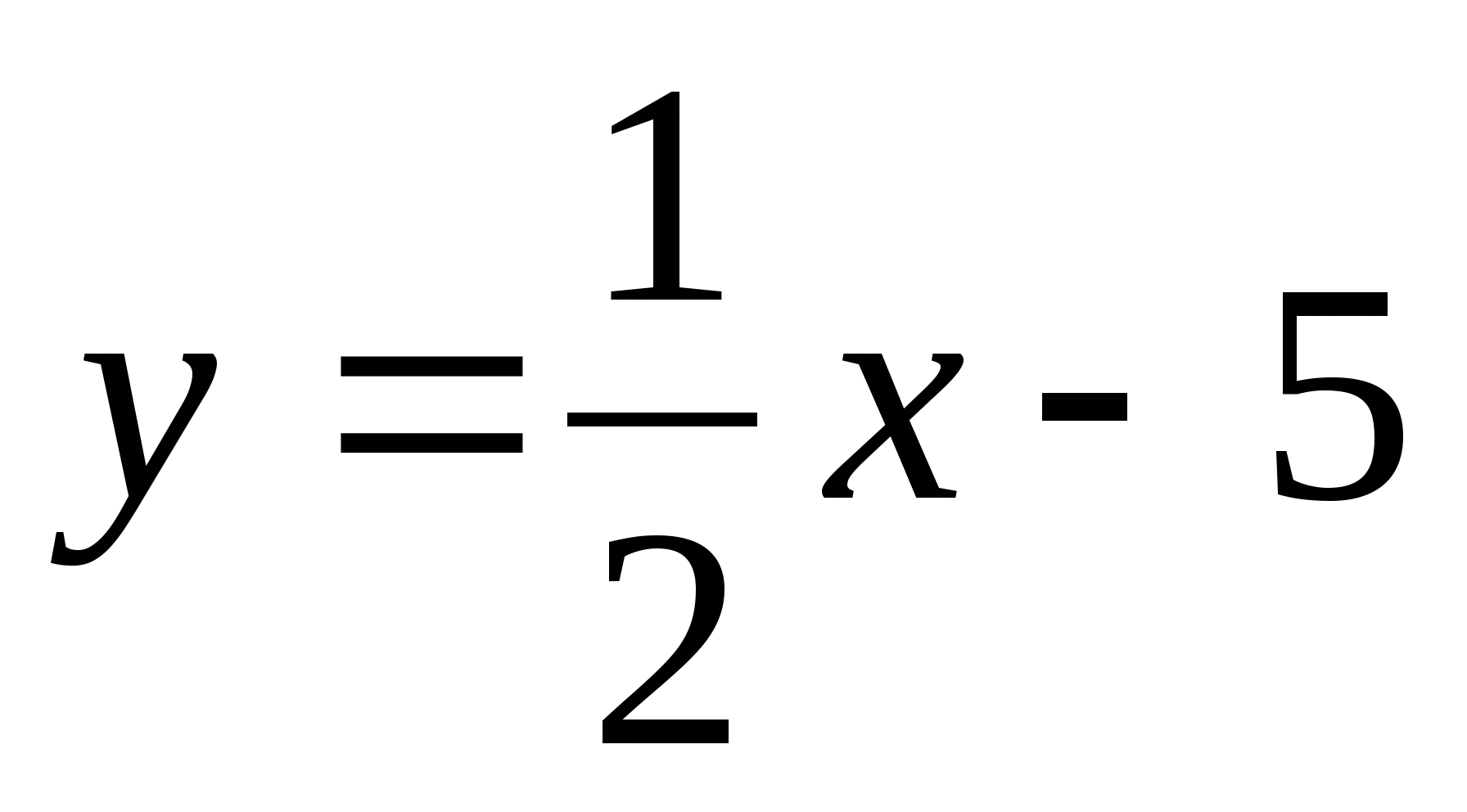 функциясының
функциясының
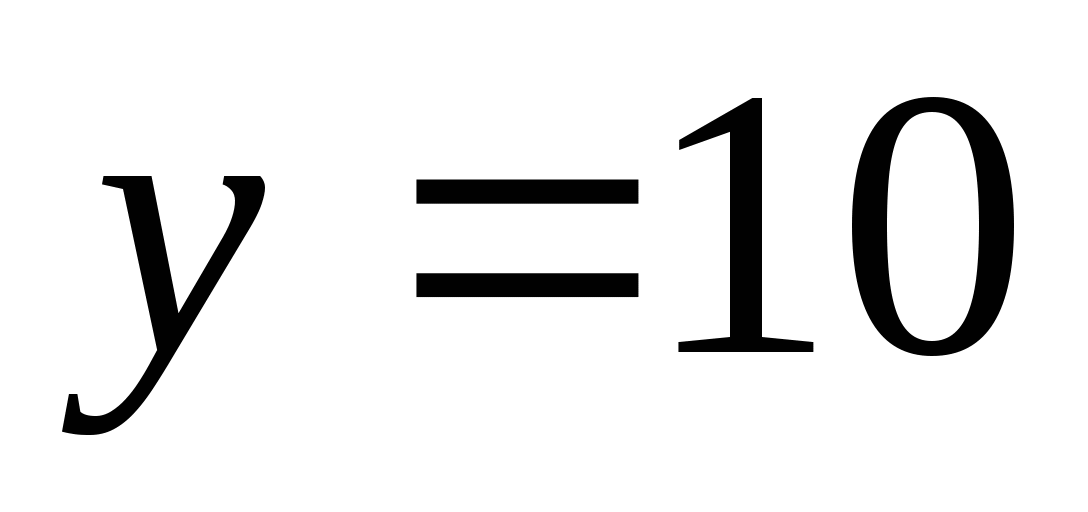 болғандағы х-тің мәнін табыңыз. Жауабы: 30
болғандағы х-тің мәнін табыңыз. Жауабы: 30
-
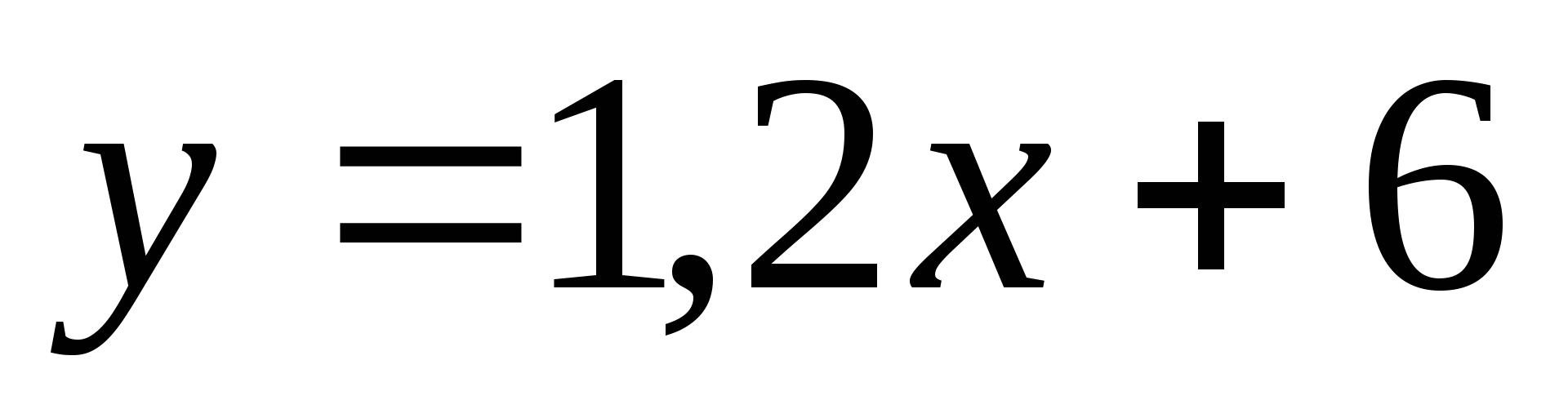 функциясының
графигінің абциссалар осімен қиылысу нүктесінің координаталарын
табыңыз. Жауабы:
функциясының
графигінің абциссалар осімен қиылысу нүктесінің координаталарын
табыңыз. Жауабы: 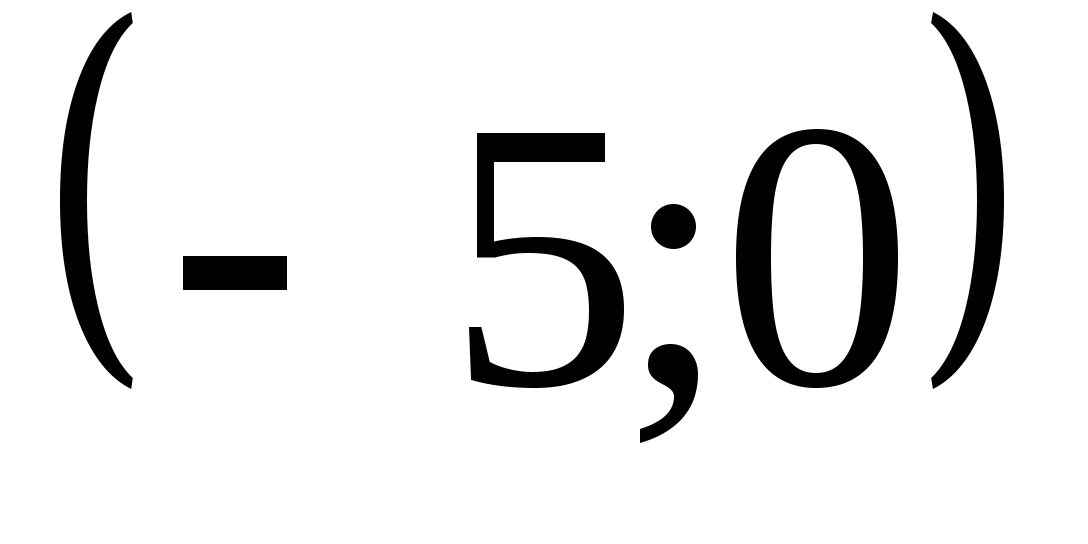
-
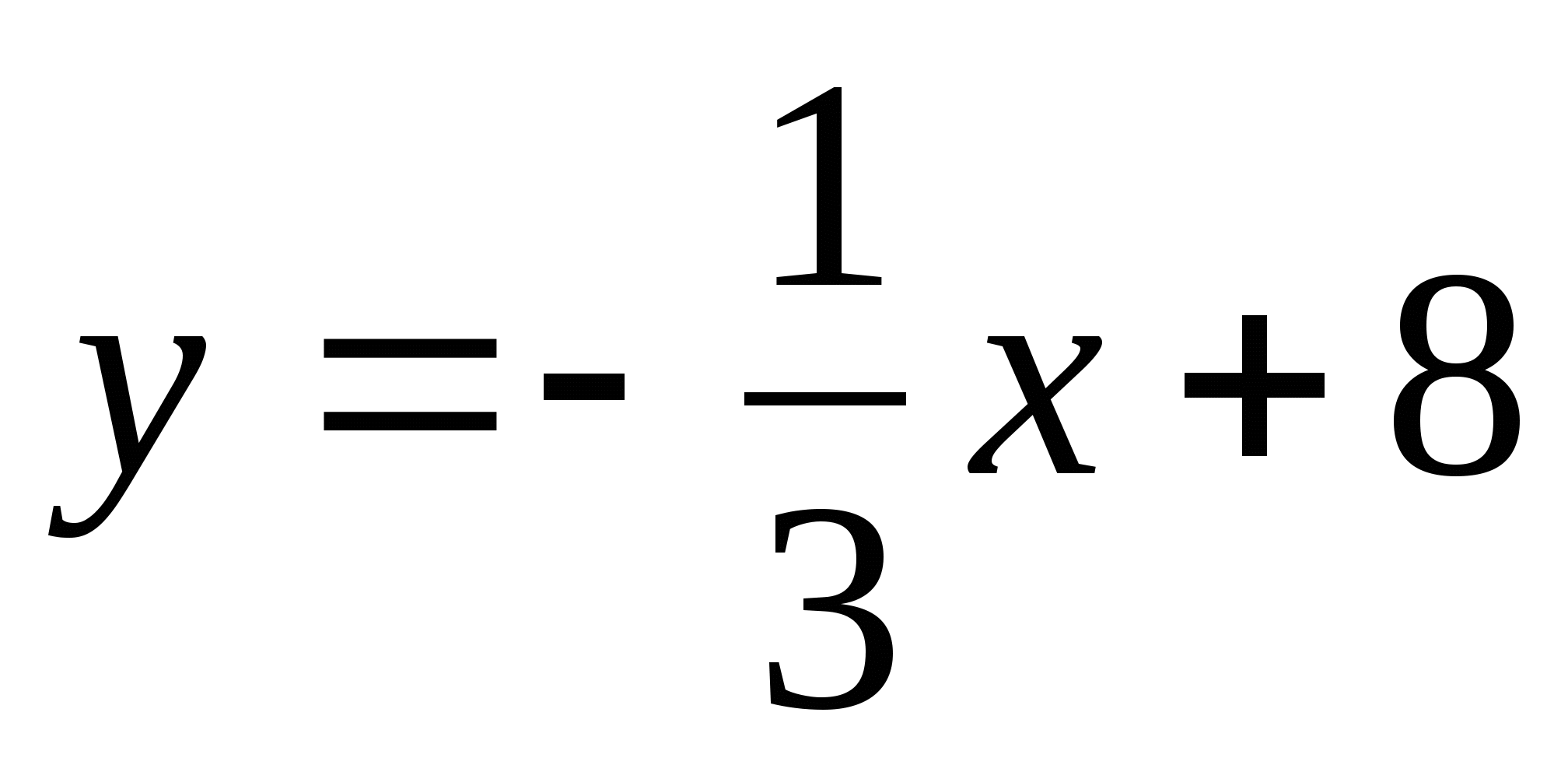 функция
графигінің ординаталар осімен қиылысу нүктесінің
координаталарын табыңыз. Жауабы:
функция
графигінің ординаталар осімен қиылысу нүктесінің
координаталарын табыңыз. Жауабы: 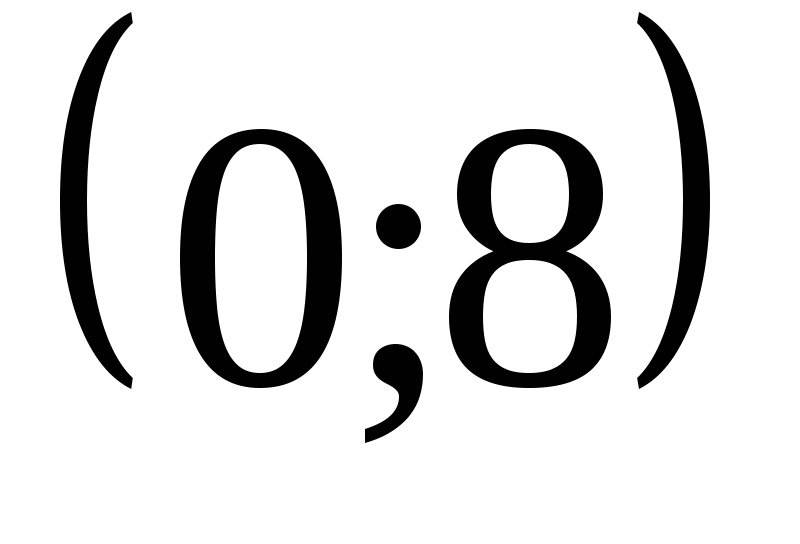
-
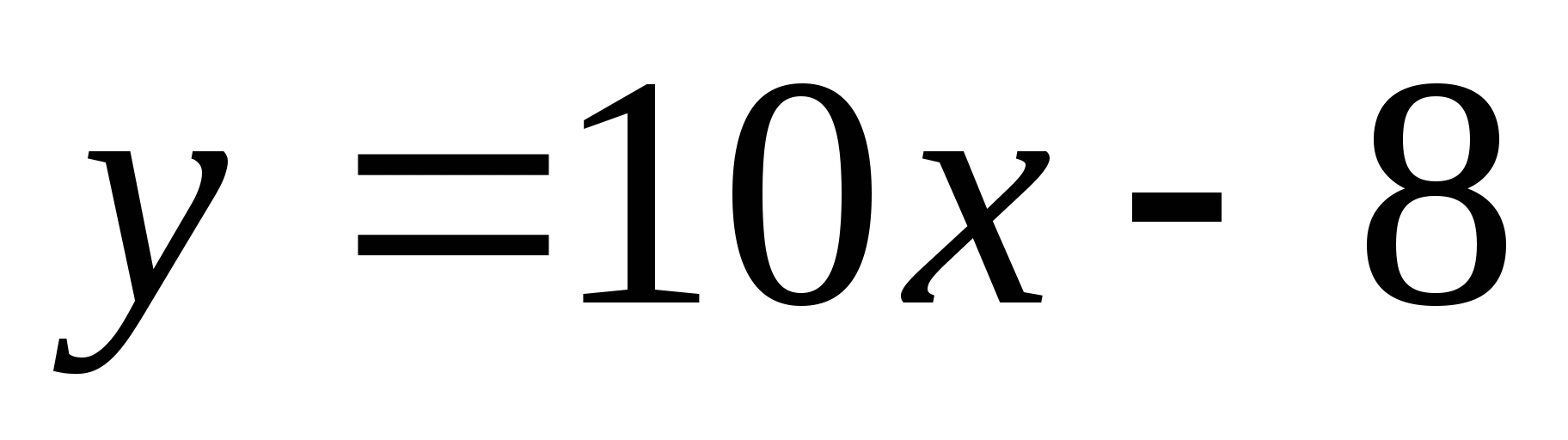 және
және
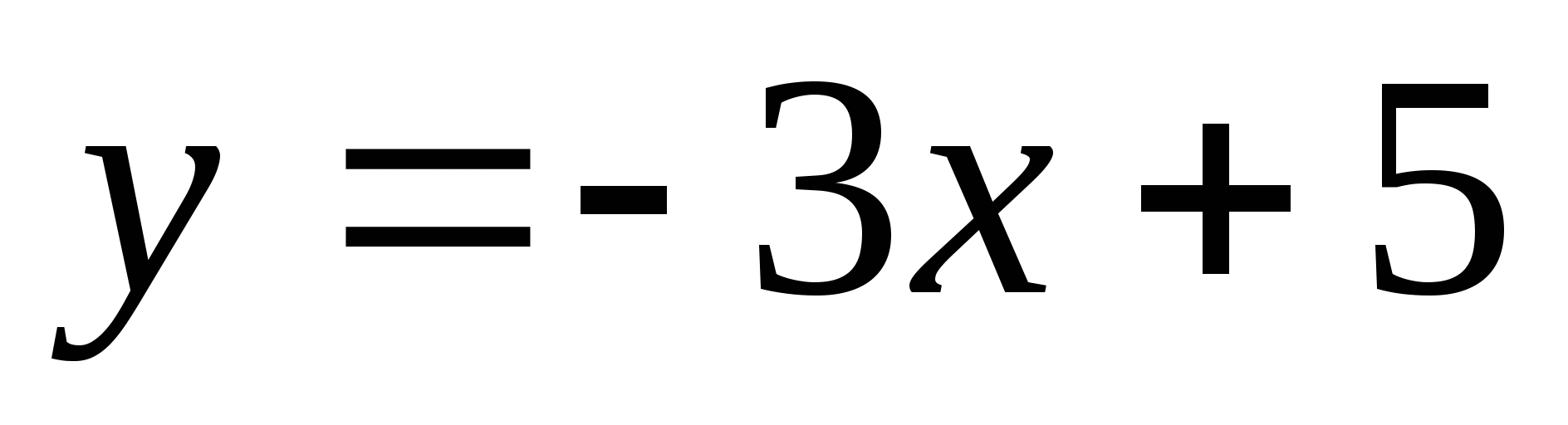 функциялар графиктерінің қиылысу нүктесінің координаталарын
табыңыз. Жауабы:
функциялар графиктерінің қиылысу нүктесінің координаталарын
табыңыз. Жауабы: 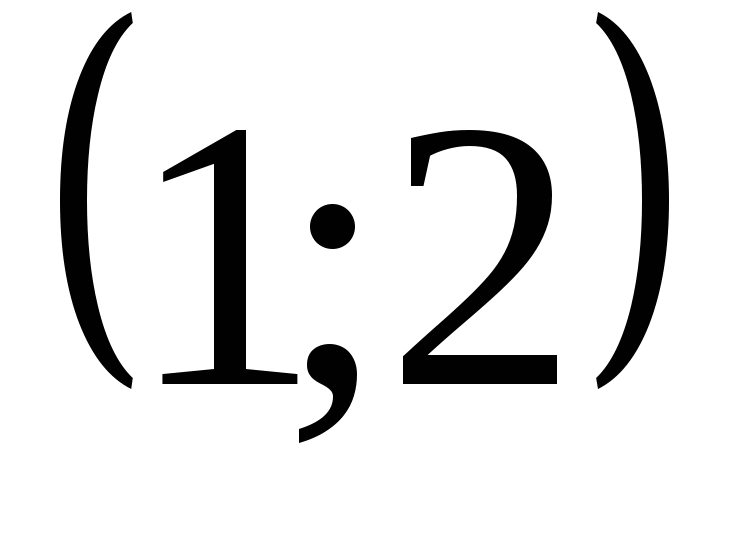
-
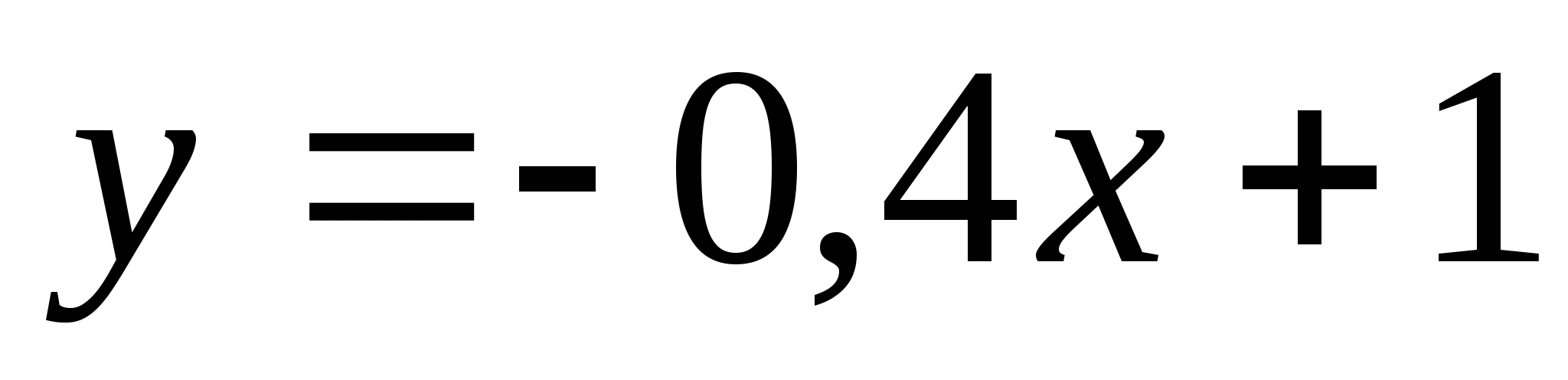 функцияларының
графигіне параллель болатын тура пропорционалдық графигін
қандай координаталық ширектерде орналасқан? Жауабы: ІІ және ІV
ширектерде
функцияларының
графигіне параллель болатын тура пропорционалдық графигін
қандай координаталық ширектерде орналасқан? Жауабы: ІІ және ІV
ширектерде
4. Жедел тест берілді.
1.Қандай айнымалы аргумент деп аталады?
1. тәуелді 2. Тәуелсіз 3. Басқа жауап
2. Аргументтің қандай мәнінде у=0,4x-5 функциясының мәні 13- ке тең.
1) -45 2) -54 3) 45 4) 54
3. y=kx+b сызықтық функциясы у=7x-8 функциясының графигі мен k- ның қандай мәнінде паралель болады?
1) -7 2) ешқандай 3) 7 4) басқа жауап
4. Функцияның мәнін тап ![]() мұндағы х=-0,2
мұндағы х=-0,2
1) 5 2) 0,5 3) -5 4) жоқ
5. Сызықтық функцияны көрсет?
1) у=3x 2) y=4x2 +2 3) y=2,5x 4) y=
![]()
a) 1; 2 b) 1; 3 c) 2; 3 d) 4
5. Қорытындылау. «Сәйкестендіру тесті»
Сызықтық функция F(x)=1,8x+k формуласымен берілген.
F(3)=8,2 k - ? a) 5,7
F(-2)=2,1 k - ? b) -1,9
F(0,5)=-1 k - ? c) 2,8
Сабақ: № 3
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Натурал көрсеткішті дәреже
Сабақтың мақсаты:
а) Білімділік: Натурал көрсеткішті дәреже ұғымымен таныстыру,есептер шығару;
ә) Дамытушылық: Ойлау, есептеу ережені есте сақтау қабілеттерін дамыту. Оқулықтан тыс ақпаратты пайдалану;
б) Тәрбиелік: Оқушылардың топтық жұмысы арқылы өз ойларын ашық айтып, жолдастарының ойын тыңдап, жауабын бағалауға, ұйымшылдық қасиеттерге тәрбиелеу.
Сабақтың түрі: Қайталау сабағы
Сабақтың әдісі: Сұрақ - жауап, топтастыру
Сабақтың көрнекілігі: оқулық.Математика.ҰБТ-ға дайындаламыз
Пәнаралық байланыс:геометрия, физика т.б.
Сабақ барысы:
І. Ұйымдастыру кезеңі:
Оқушылармен сәлемдесу;Оқушыларды түгелдеу;Назарларын сабаққа аудару.
II.Есептер шығару:
-
Өрнекті ықшамдаңыз:
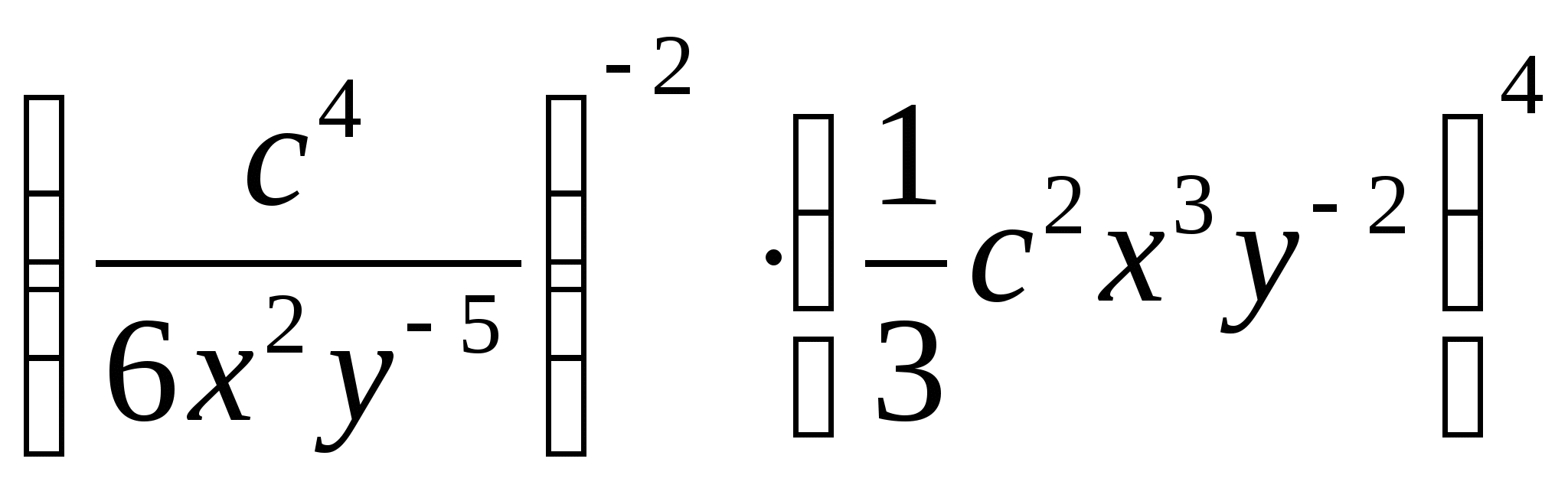
-
Өрнектің мәнін табыңыз:
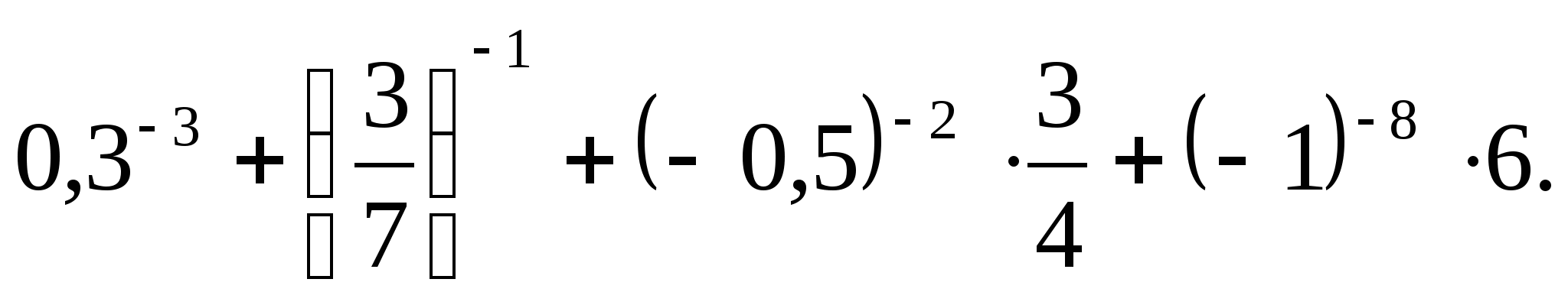
-
Өрнекті ықшамдаңыз:
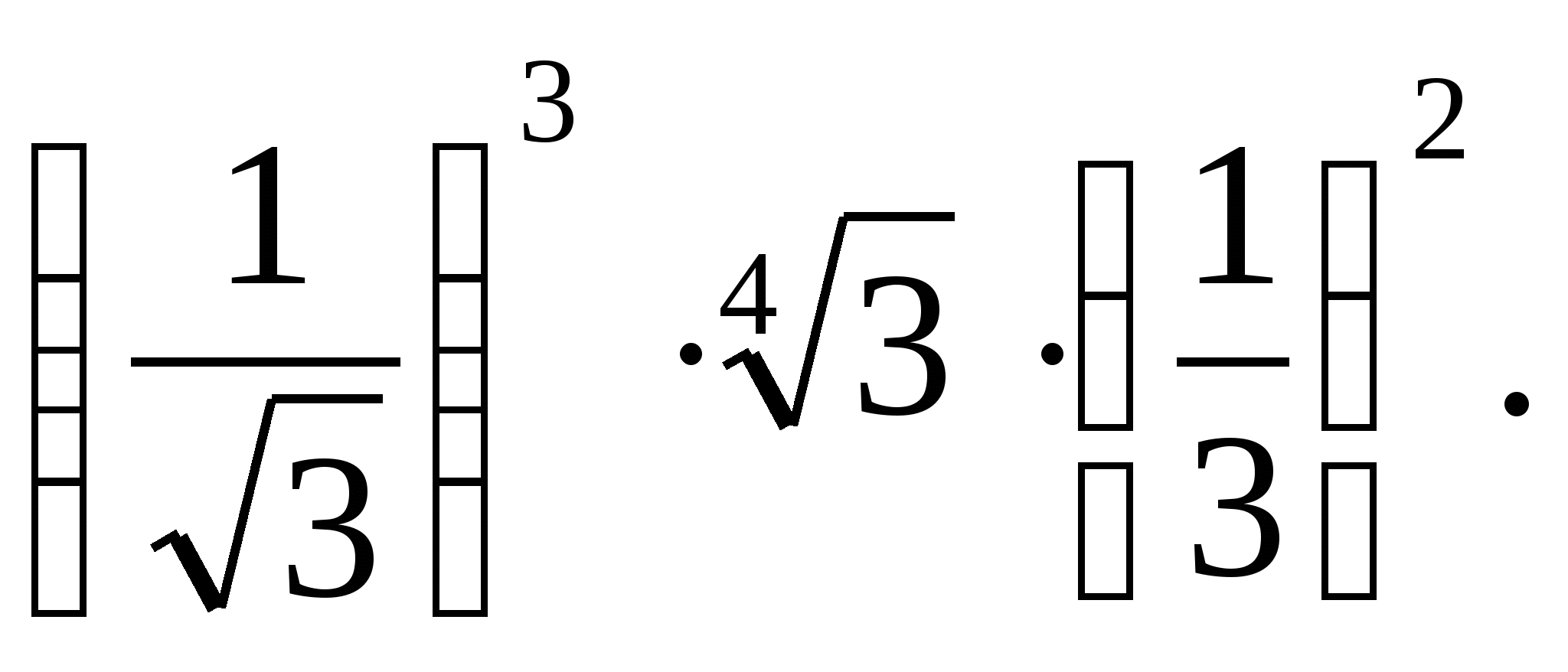
-
Өрнекті ықшамдаңыз:
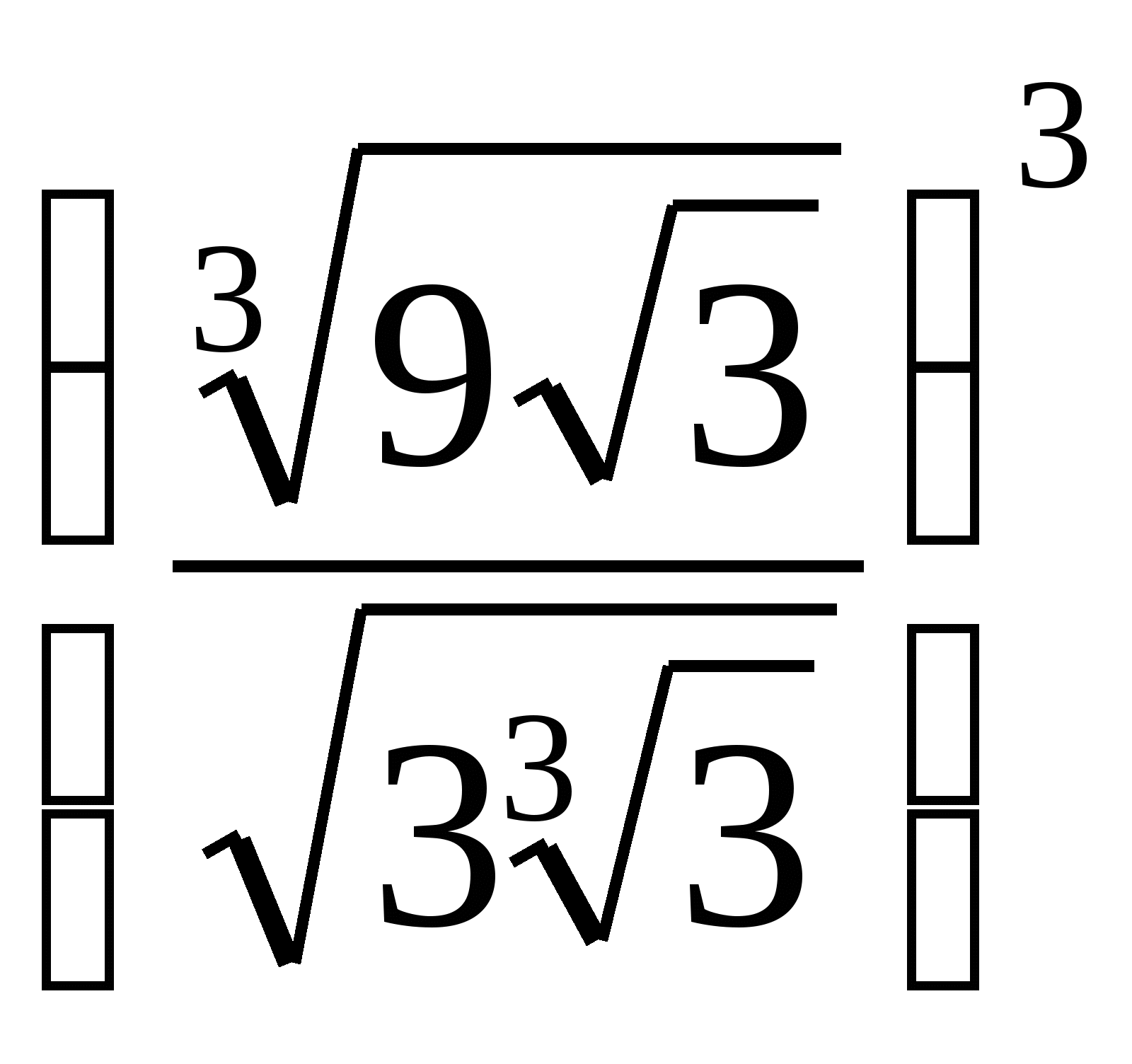
-
Өрнекті ықшамдаңыз:
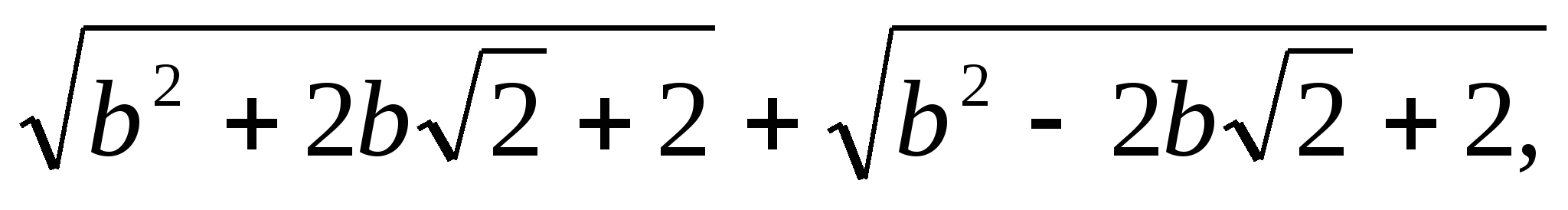 егер
егер 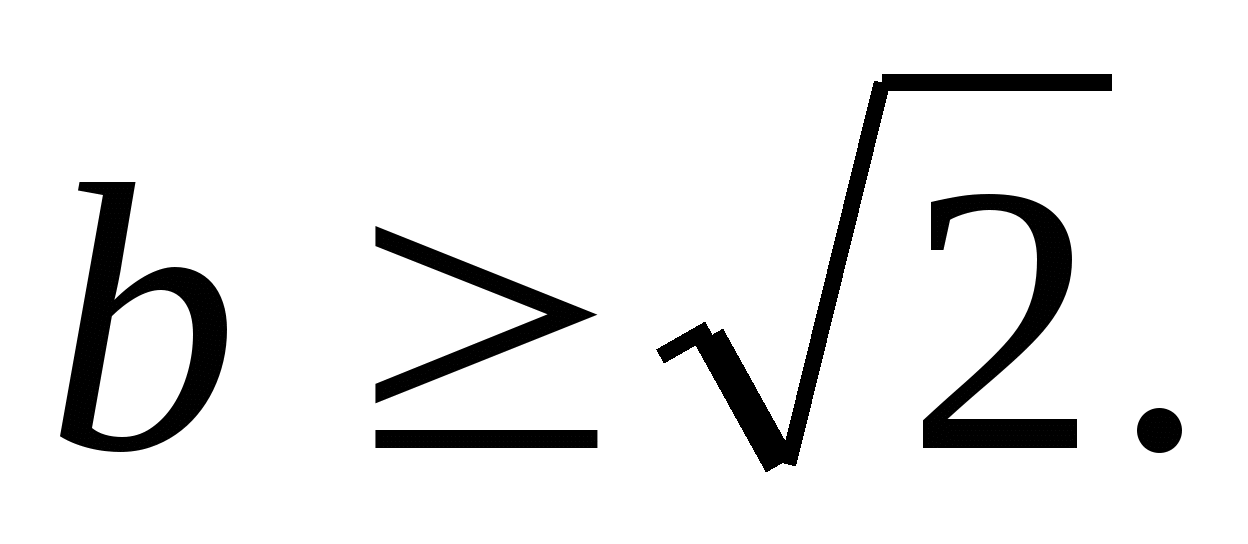
-
Бөлшекті қысқартыңыз:
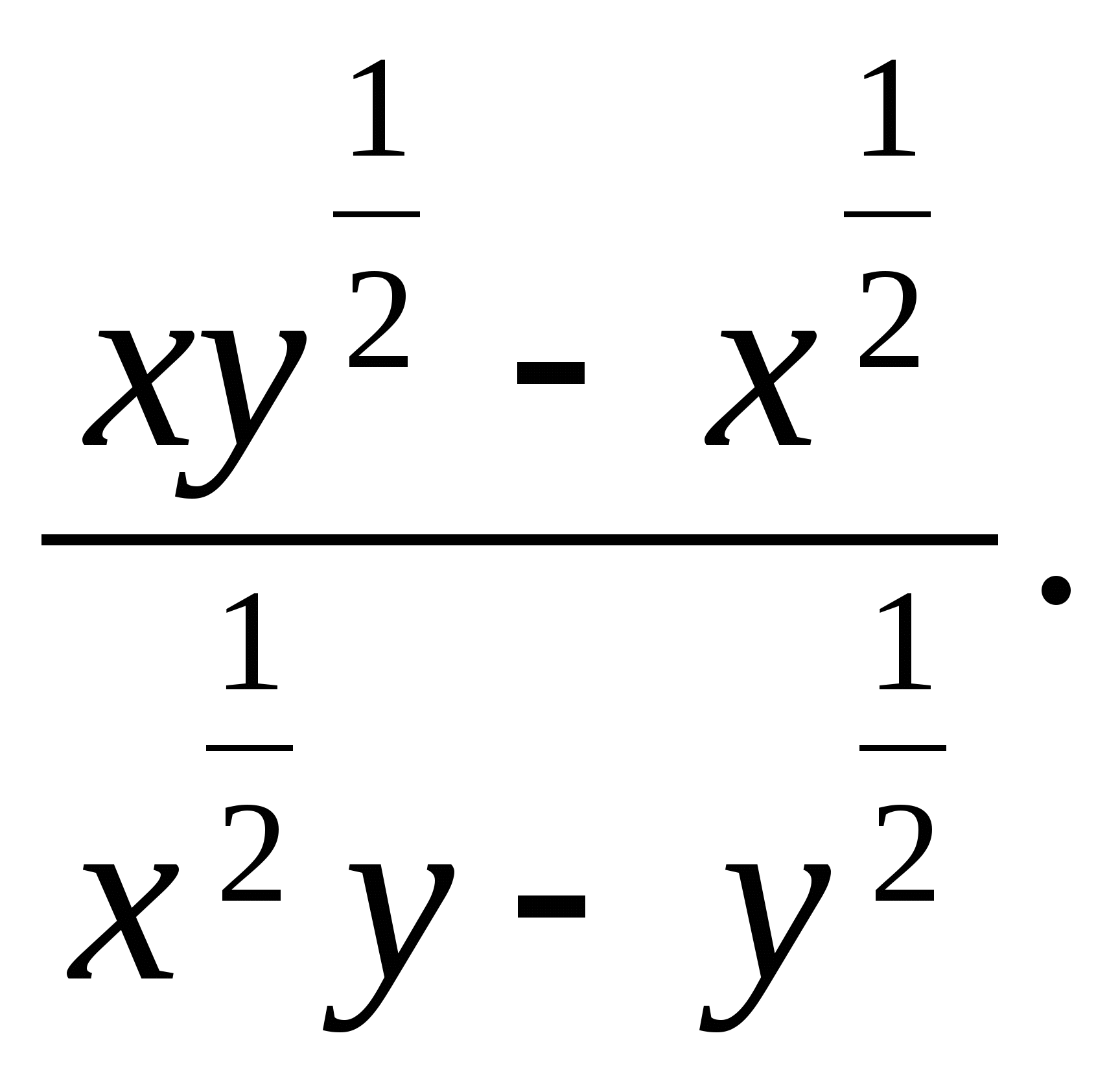
-
Есептеңіз:
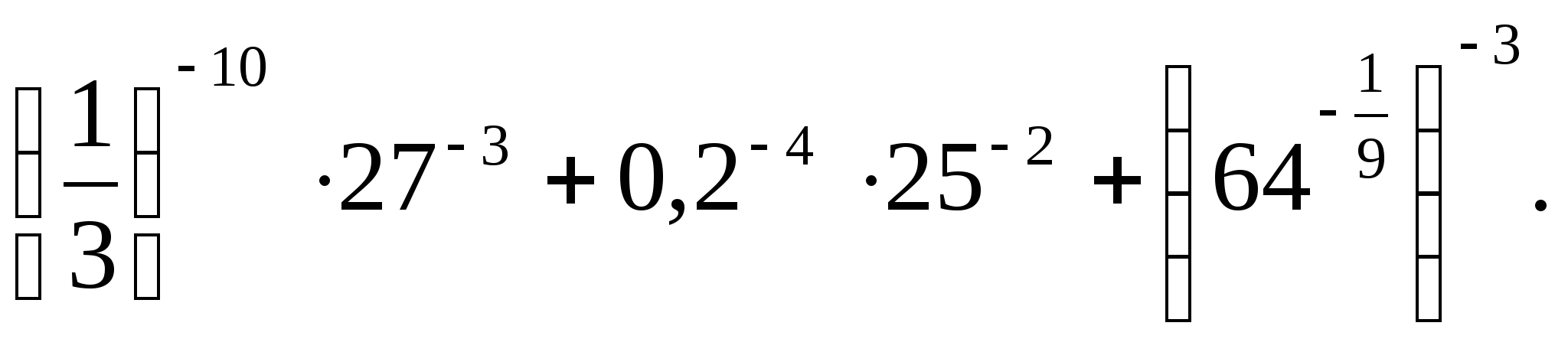
А) 2; В) 5; С) -8; Д) 7; Е) 8.
-
Есептеңіз:
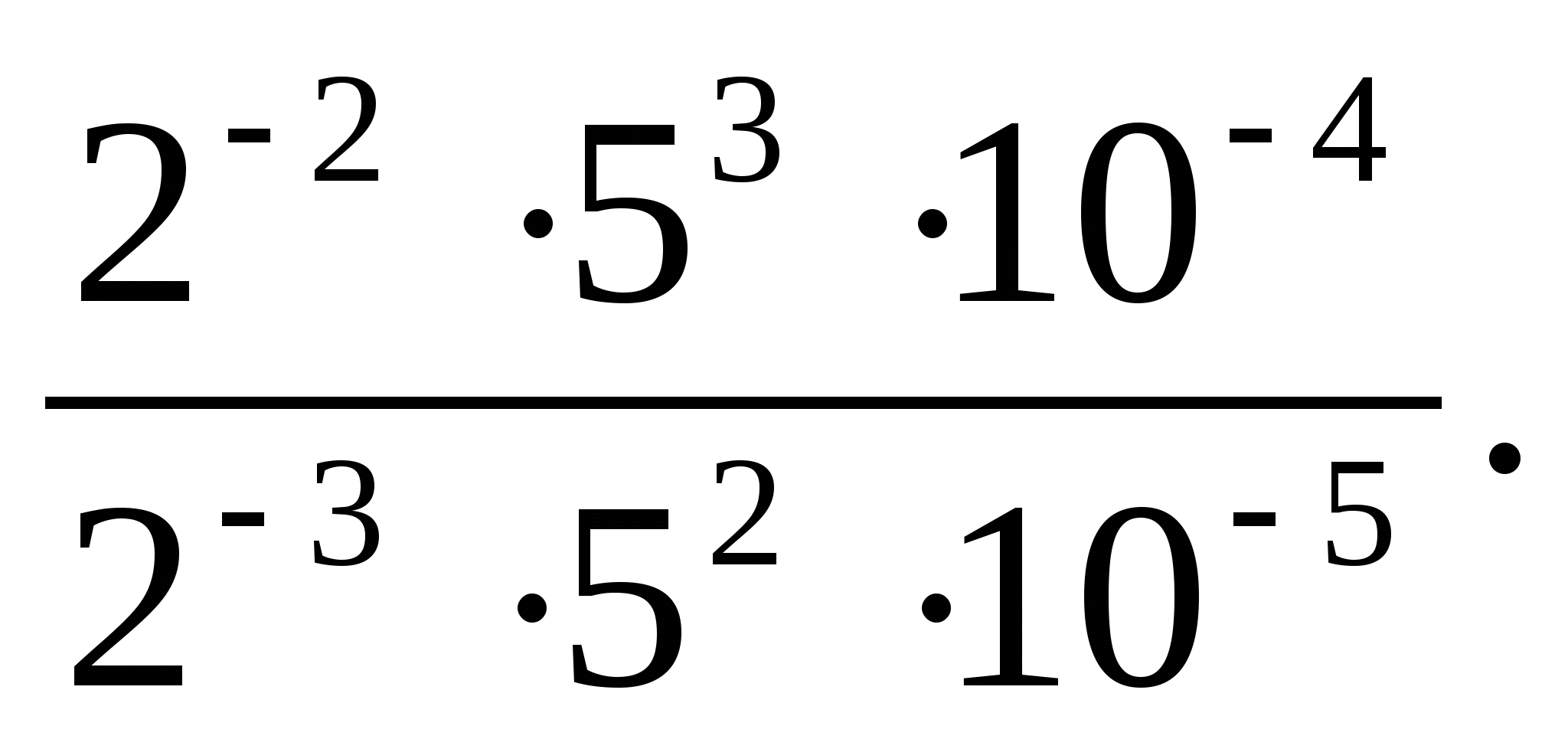
А) 90; В) 110; С) 100; Д) -110; Е) -100.
-
Есептеңіз:
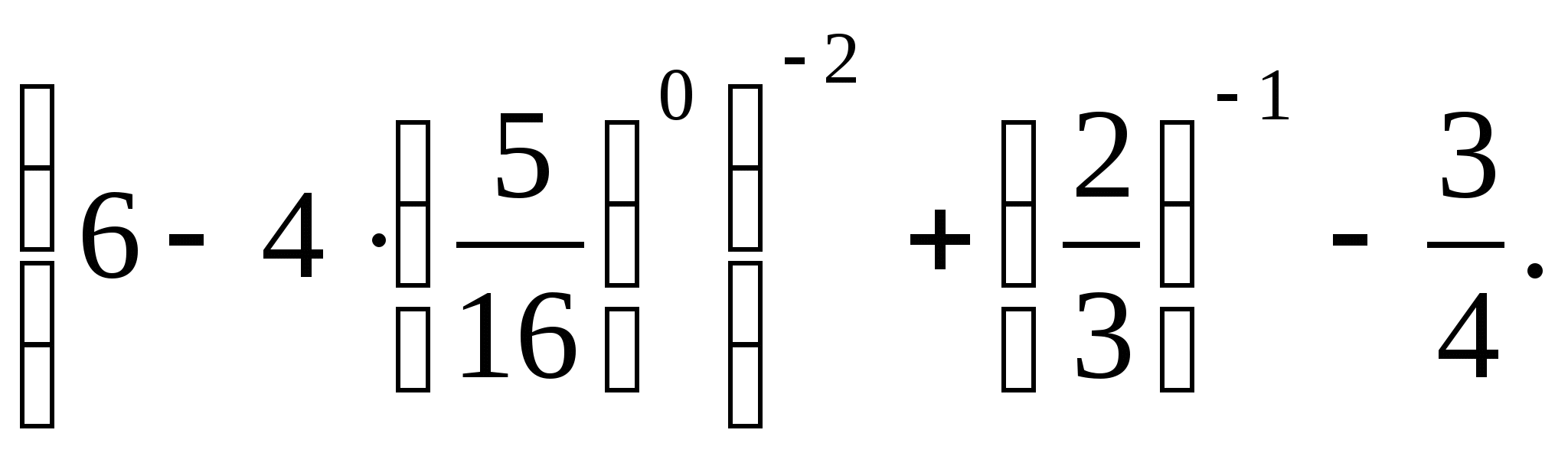
А) 1; В) 5; С) 4; Д) -1; Е) 0.
-
Есептеңіз:
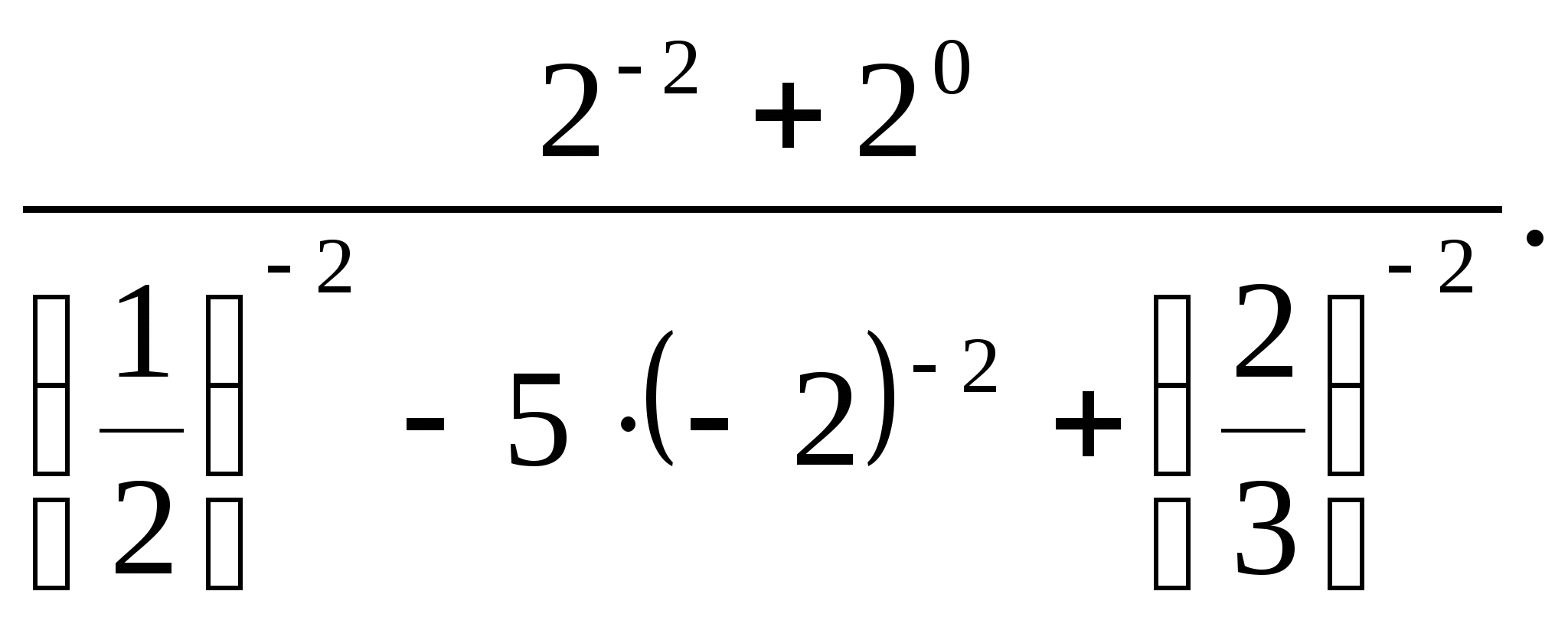
А) ![]() В) -
В) -![]()
![]() ;
Д)
;
Д) ![]()
-
Өрнекті бөлшек көрсеткішті дәреже ретінде жазыңыз:
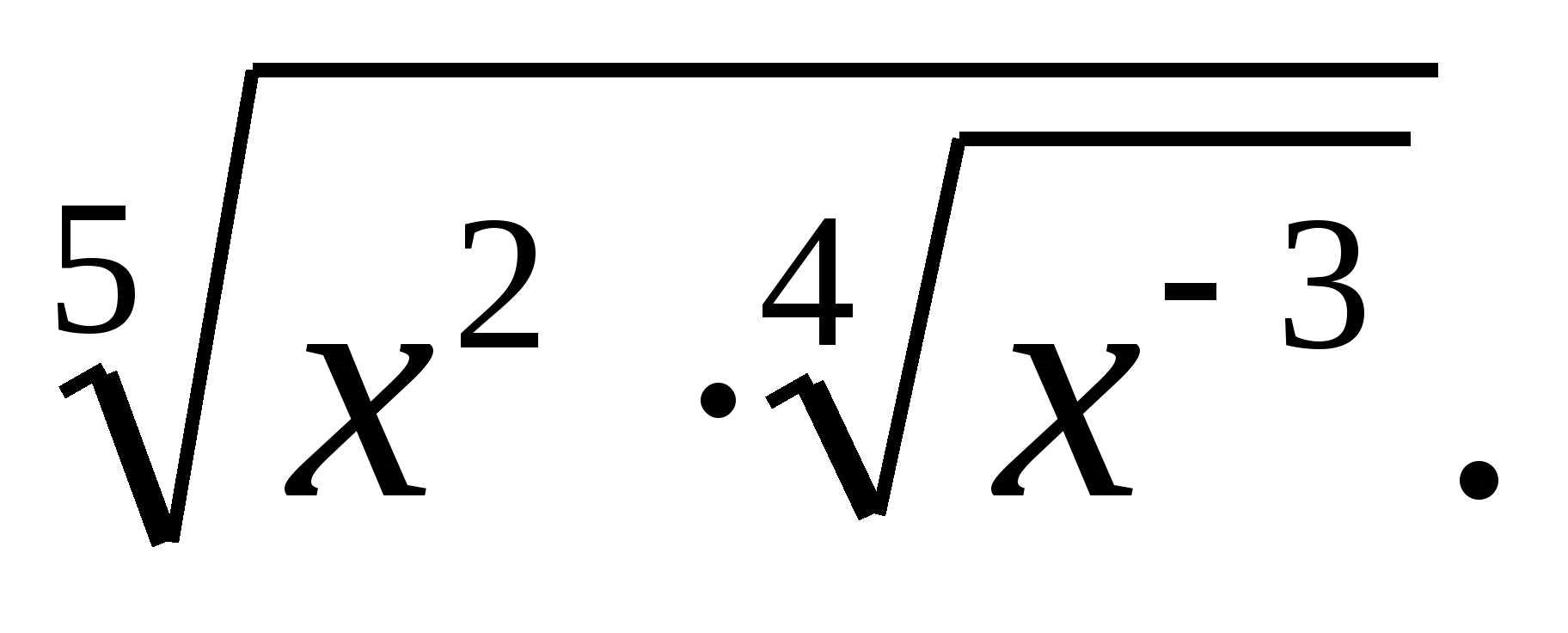
А)![]() В)
В) ![]() ; С)х; Д)
; С)х; Д)![]() Е)
Е)![]()
-
Өрнектің мәнін табыңыз:
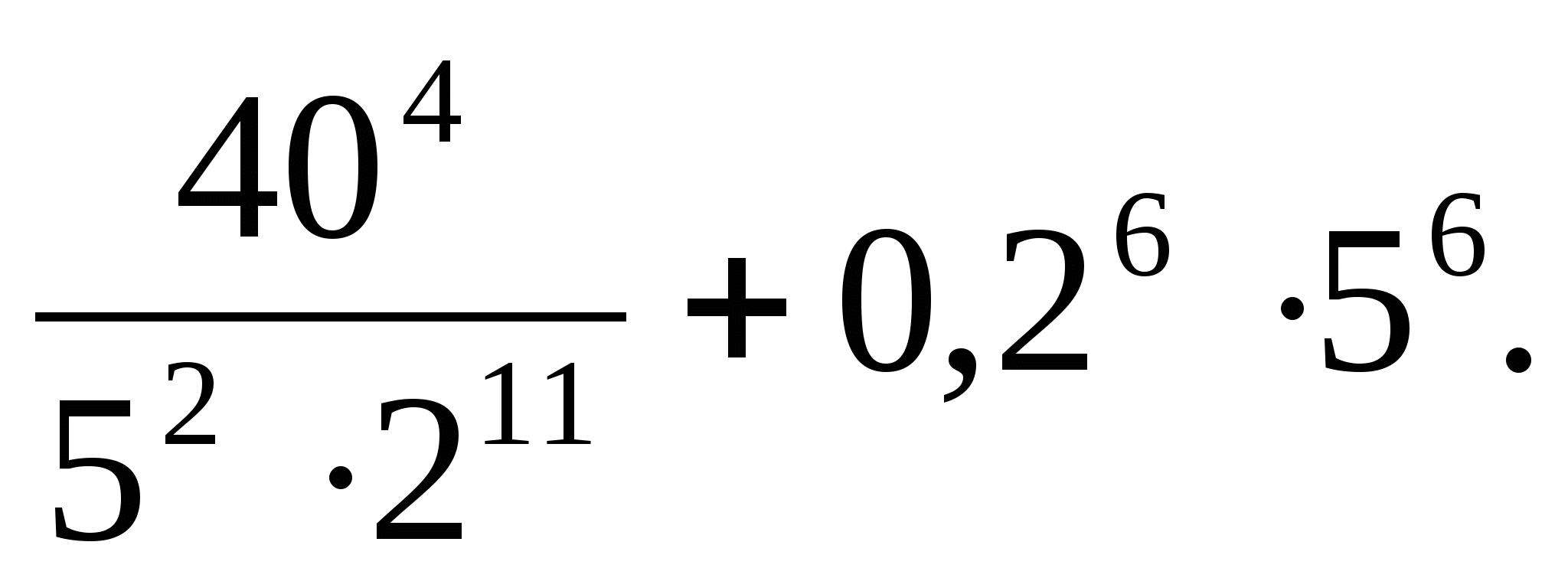
А) 31; В) 21; С) 71; Д) 11; Е) 51.
Үйге тапсырма:№10,№12
Қорытындылау:
Натурал көрсеткішті дәреже деген не ?Қасиеттері қандай?
Сабақ: № 4
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Натурал көрсеткішті дәреже
Сабақтың мақсаты:
а) Білімділік: Натурал көрсеткішті дәреже ұғымымен таныстыру,есептер шығару;
ә) Дамытушылық: Ойлау, есептеу ережені есте сақтау қабілеттерін дамыту. Оқулықтан тыс ақпаратты пайдалану;
б) Тәрбиелік: Оқушылардың топтық жұмысы арқылы өз ойларын ашық айтып, жолдастарының ойын тыңдап, жауабын бағалауға, ұйымшылдық қасиеттерге тәрбиелеу.
Сабақтың түрі: Қайталау сабағы
Сабақтың әдісі: Сұрақ - жауап, топтастыру
Сабақтың көрнекілігі: оқулық.Математика.ҰБТ-ға дайындаламыз
Пәнаралық байланыс:геометрия, физика т.б.
Сабақ барысы:
І. Ұйымдастыру кезеңі:
Оқушылармен сәлемдесу;Оқушыларды түгелдеу;Назарларын сабаққа аудару.
II.Есептер шығару:
-
Есептеңіз:
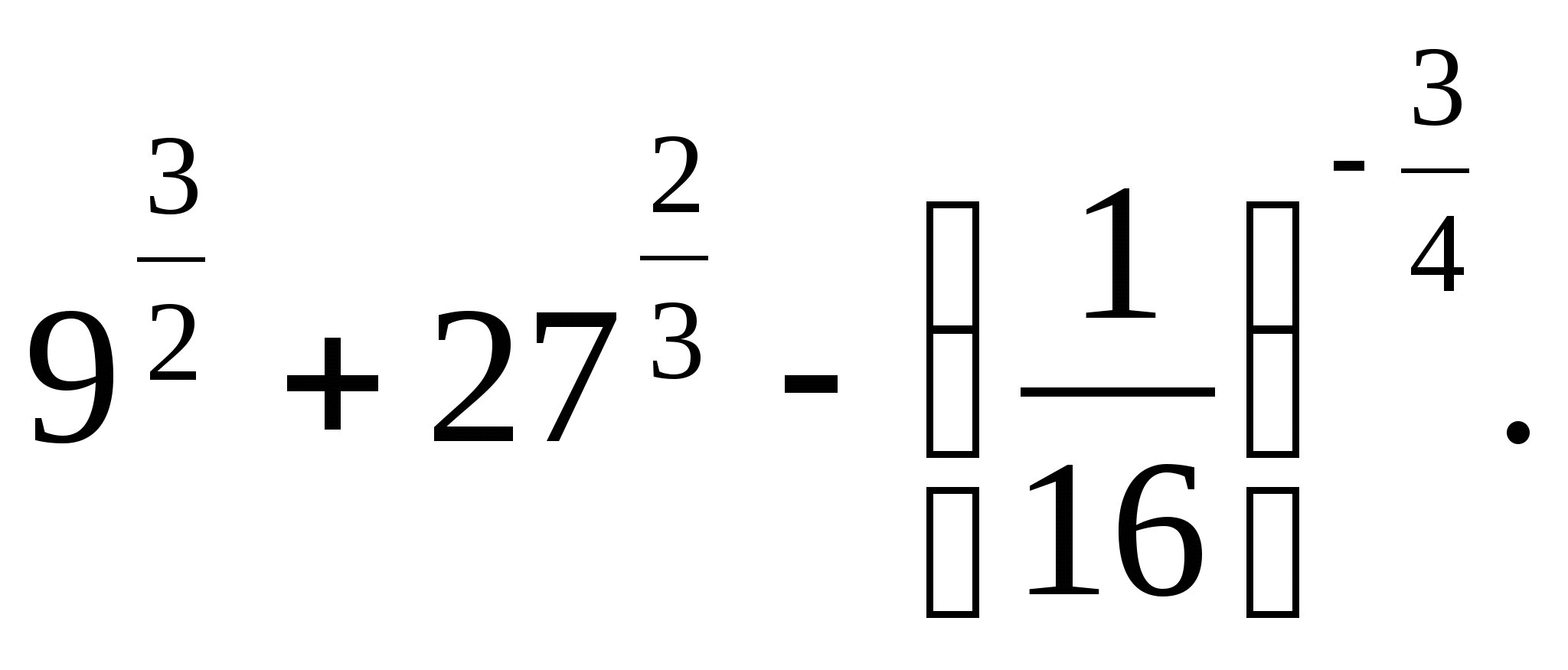
-
Қысқартыңыз:
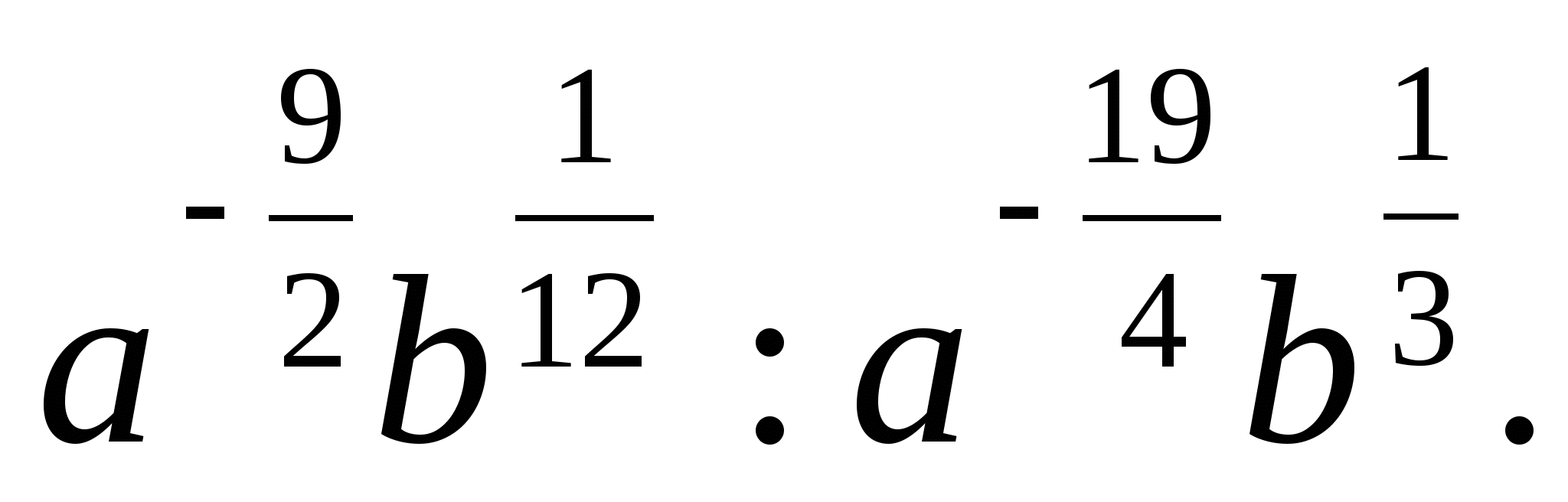
-
Өрнекті ықшамдаңыз:
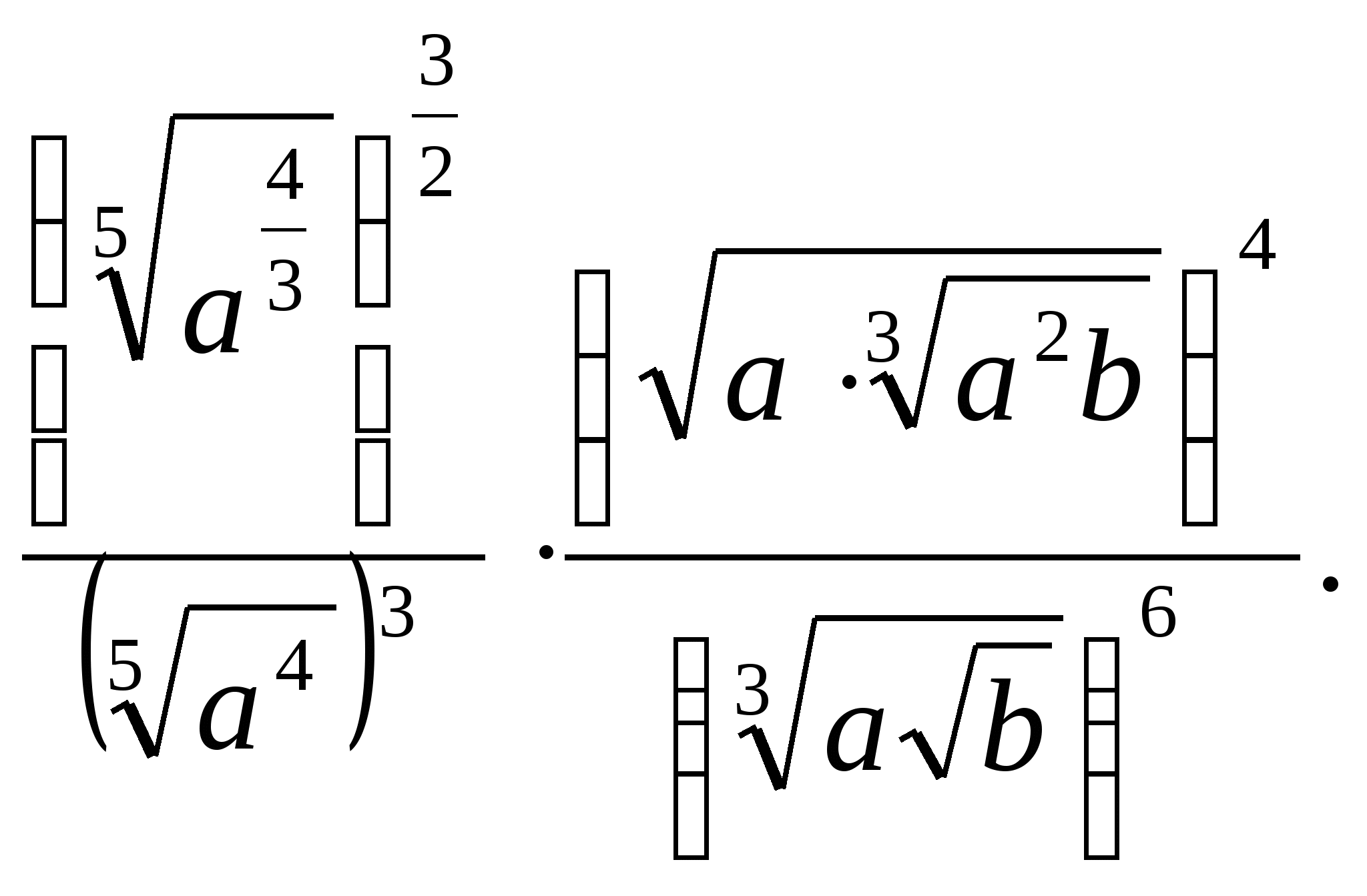
-
Бөлшекті қысқартыңыз:
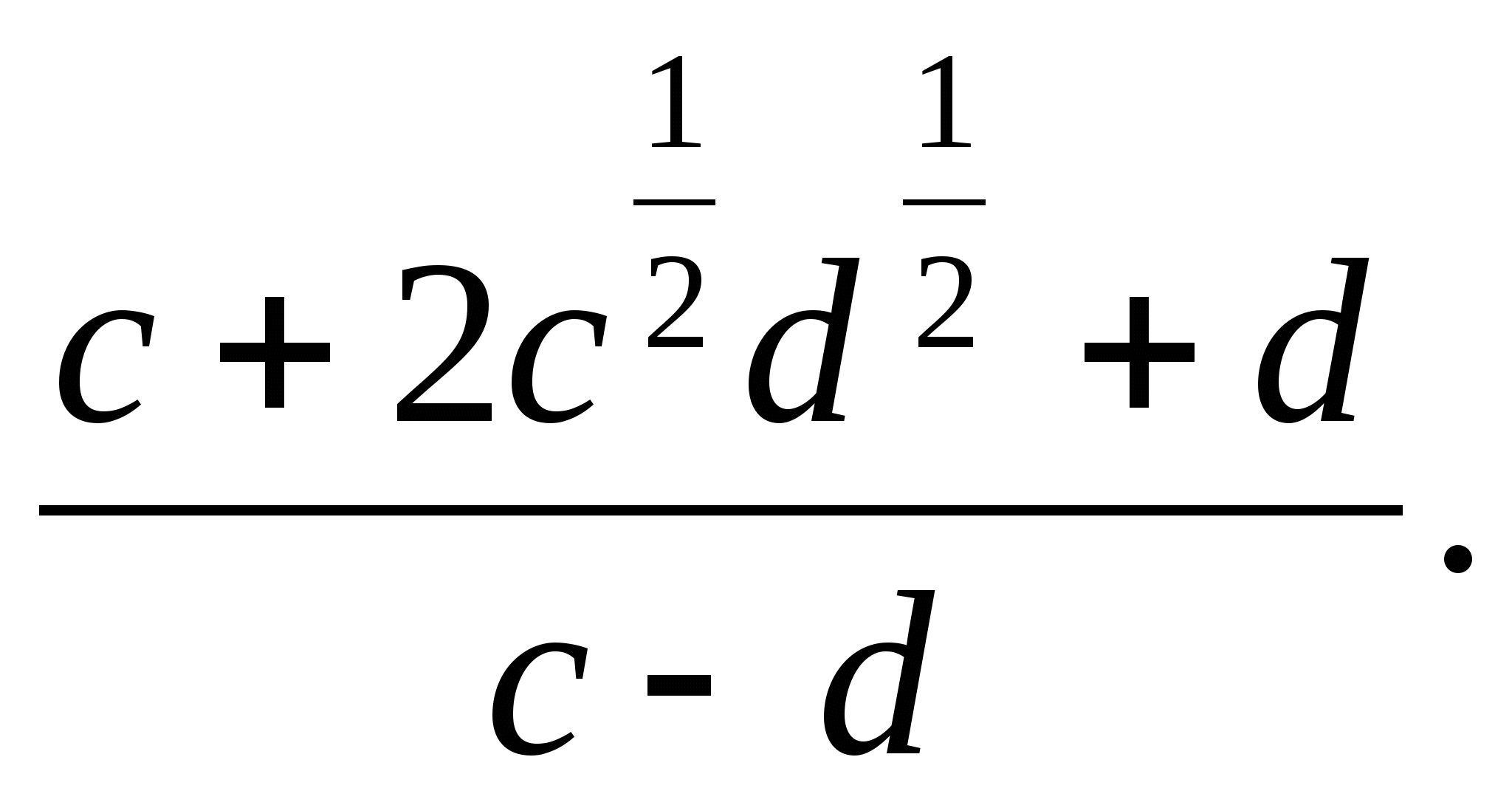
-
Өрнектің мәнін табыңыз:
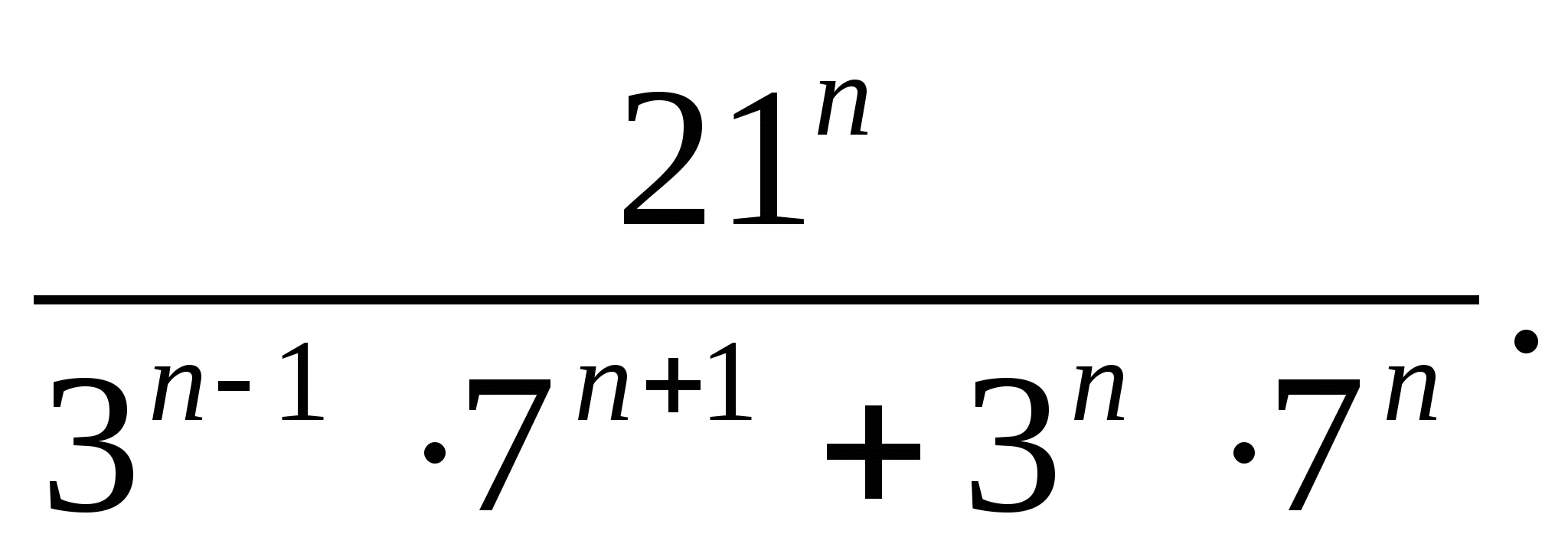
-
Өрнекті ықшамдаңыз:
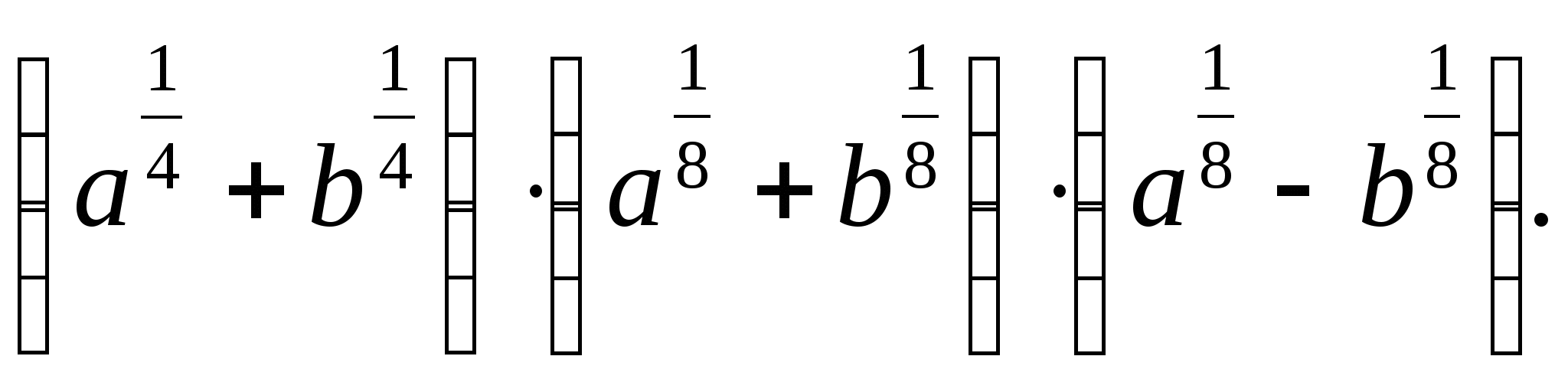
-
Өрнекті ықшамдаңыз:
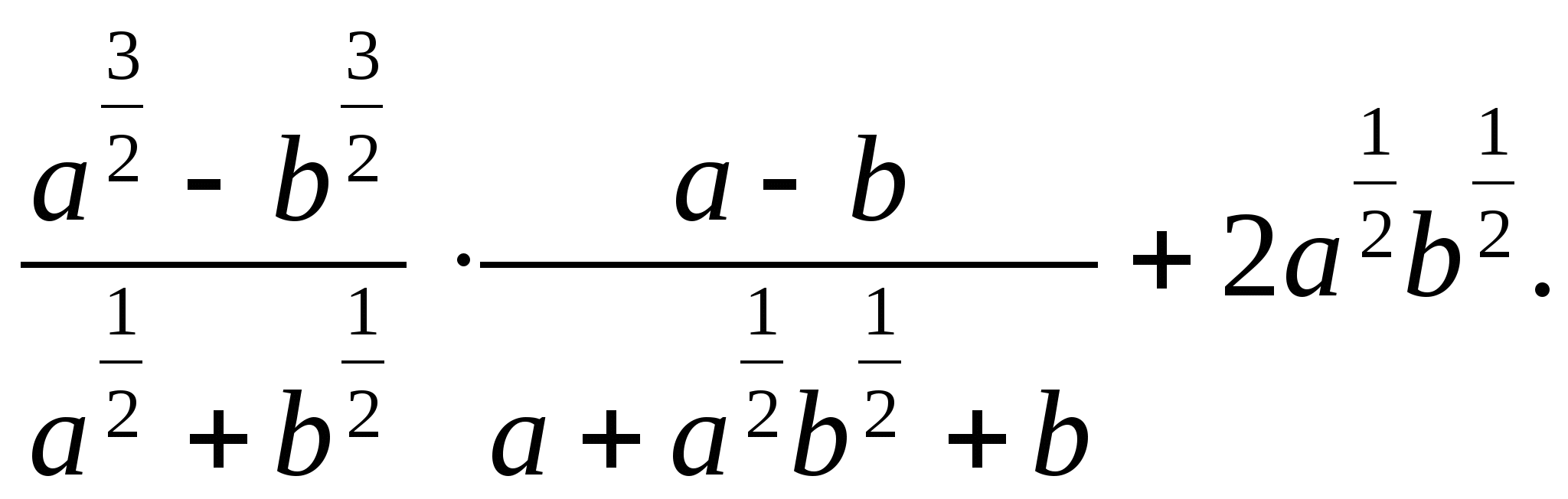
-
Өрнектің мәнін табыңыз:
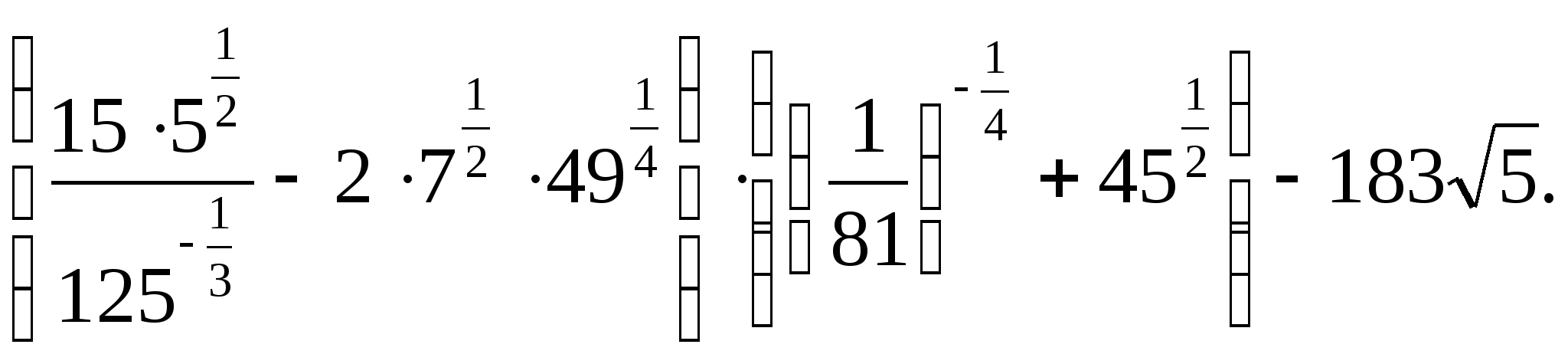
-
Есептеңіз:
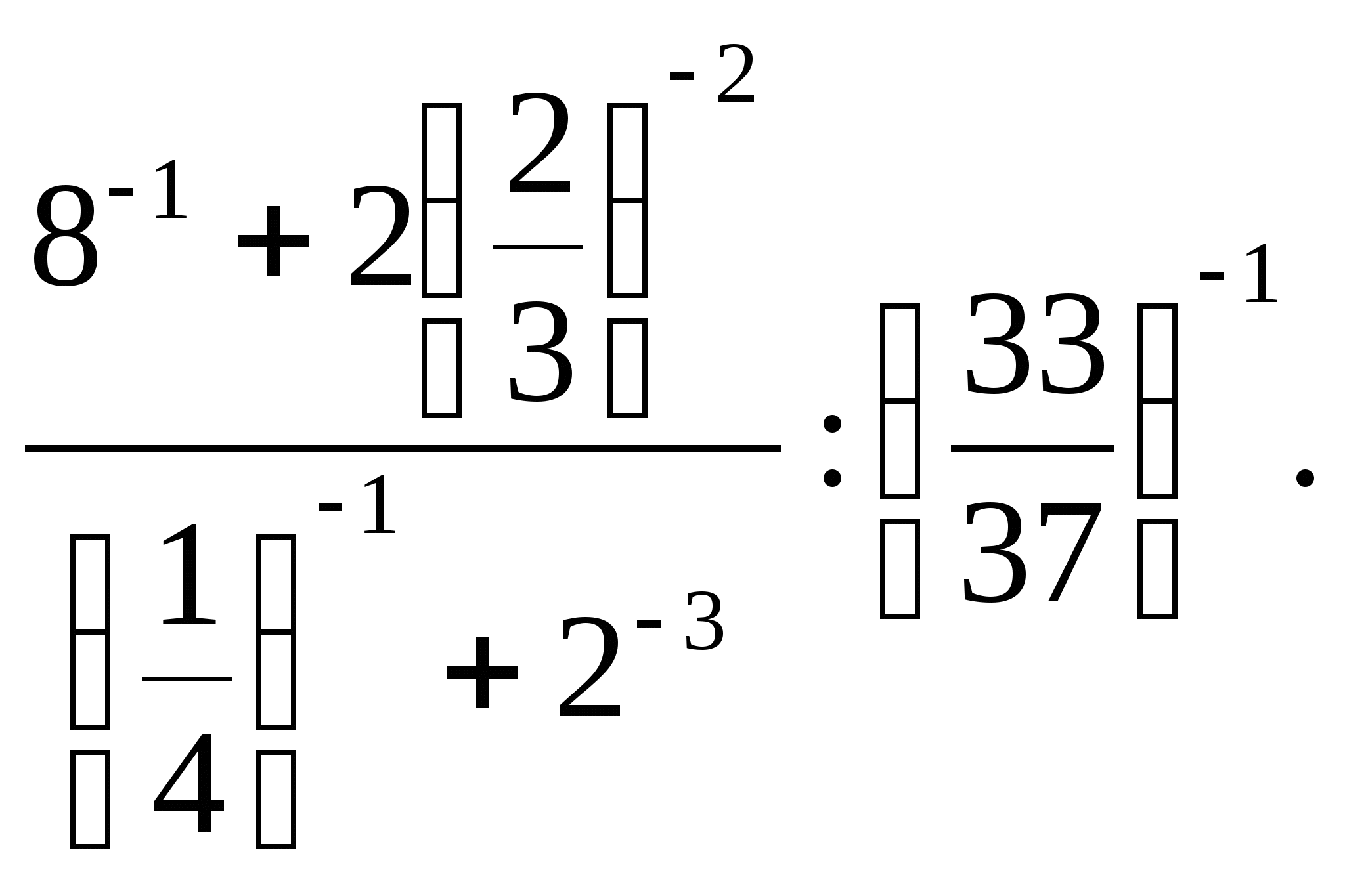
-
Есептеңіз:
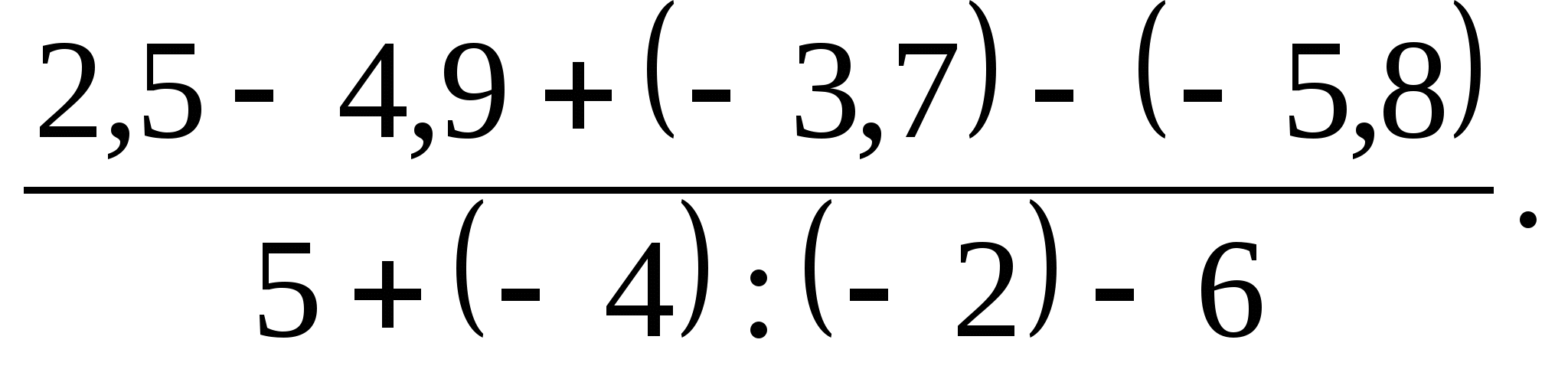
-
Есептеңіз:
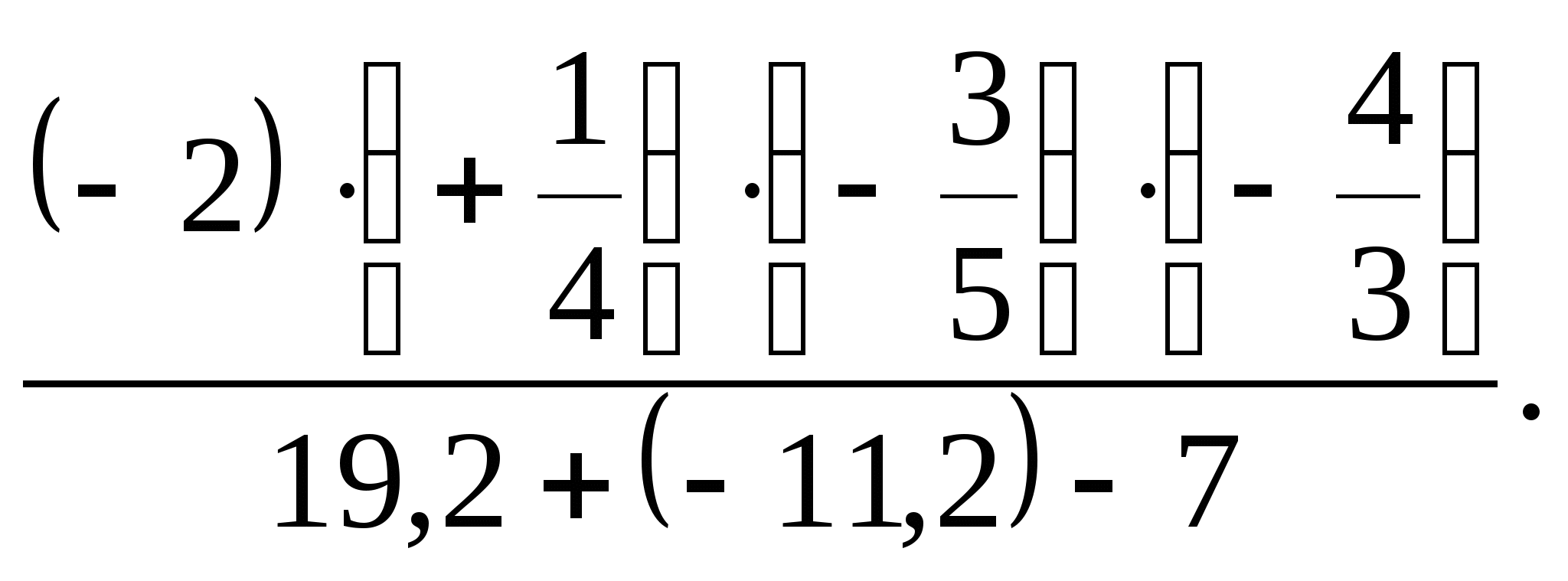
-
Есептеңіз:
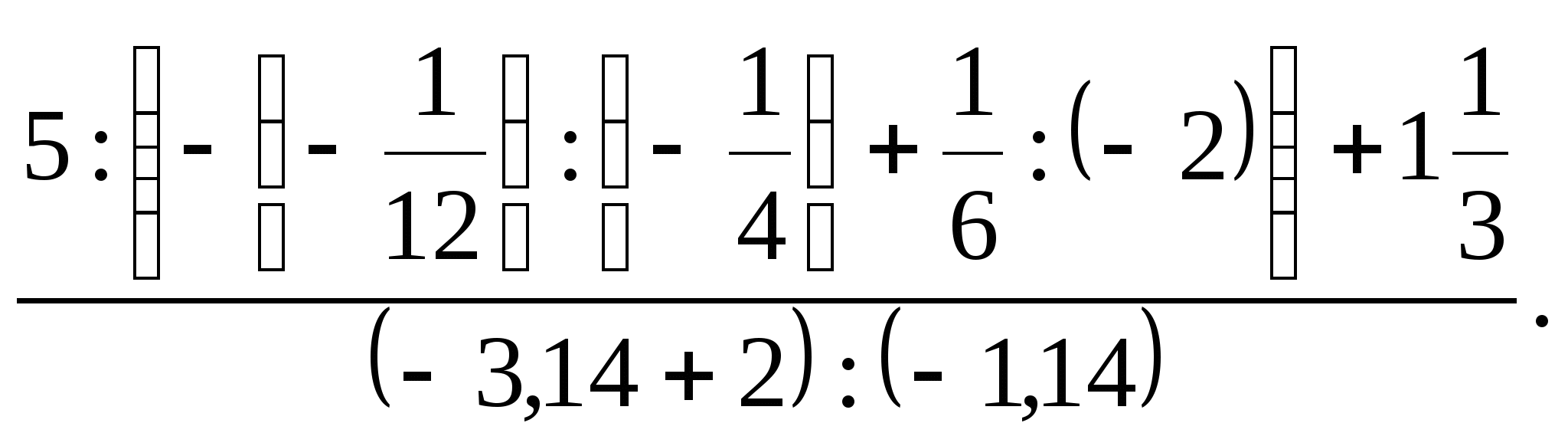
-
Өрнекті ықшамдаңыз:
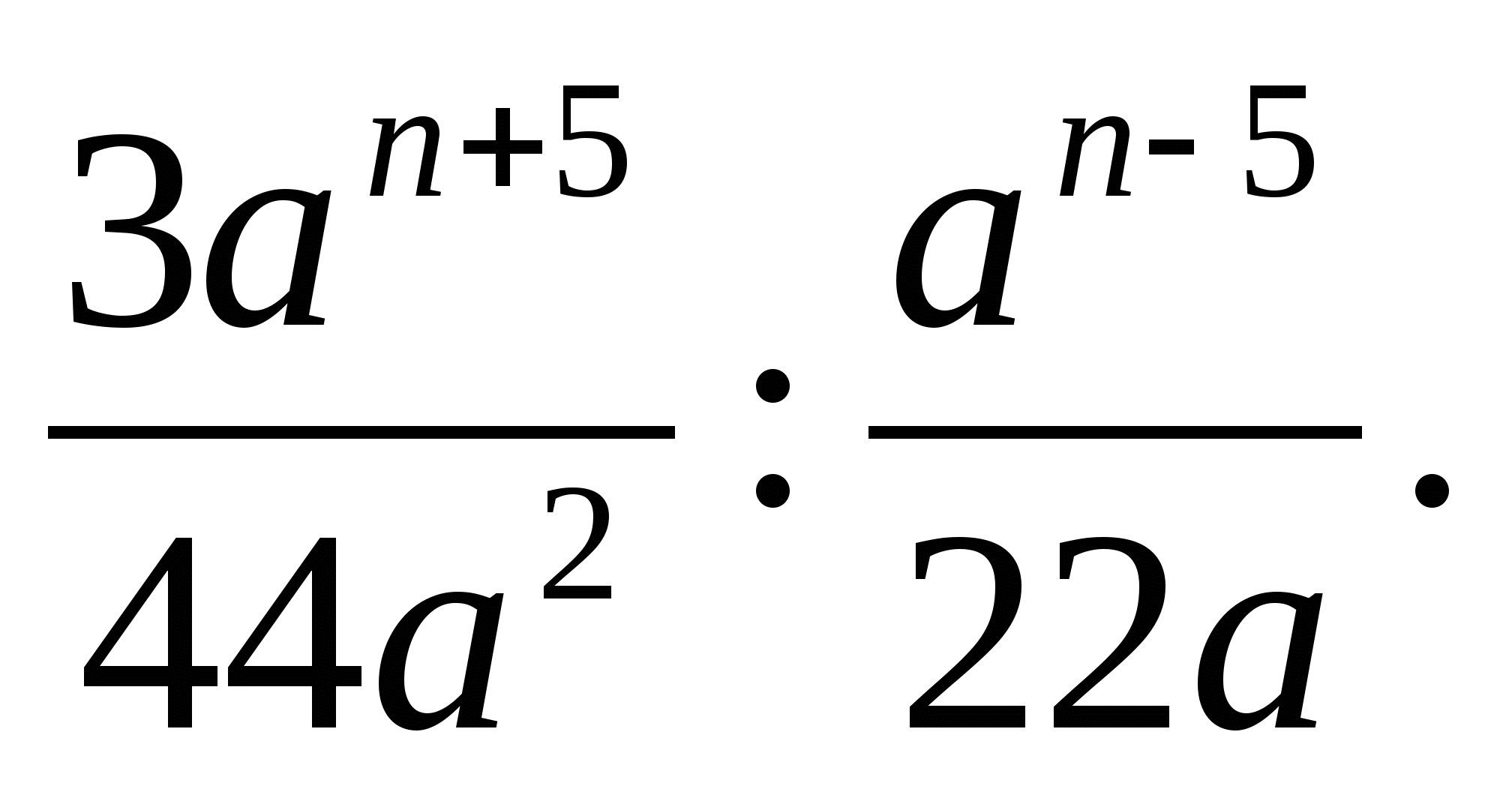
А)![]()
![]()
![]()
![]()
![]()
Үйге тапсырма:№5,№7
Қорытындылау:
Натурал көрсеткішті дәреже деген не ?Қасиеттері қандай?
Сабақ: № 5,6
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Арифметикалық прогрессия
Сабақтың мақсаты:
Білімділік: арифметикалық прогрессия тақырыбы бойынша оқушылардың білімдерінің деңгейі мен тиянақтылығын тексеру
ә) Дамытушылық: Ойлау, есептеу ережені есте сақтау қабілеттерін дамыту. Оқулықтан тыс ақпаратты пайдалану;
б) Тәрбиелік: Оқушылардың топтық жұмысы арқылы өз ойларын ашық айтып, жолдастарының ойын тыңдап, жауабын бағалауға, ұйымшылдық қасиеттерге тәрбиелеу.
Сабақтың түрі: Қайталау сабағы
Сабақтың әдісі: Сұрақ - жауап, топтастыру
Сабақтың көрнекілігі: оқулық.Математика.ҰБТ-ға дайындаламыз
Пәнаралық байланыс:геометрия, физика т.б.
Сабақ барысы:
І. Ұйымдастыру кезеңі:
Оқушылармен сәлемдесу;Оқушыларды түгелдеу;Назарларын сабаққа аудару.
II.Есептер шығару:
Арифметикалық прогрессияның n-ші мүшесінің формуласы
аn=а1+(n-1)×d ![]()
Арифметикалық прогрессияның n-ші мүшесінің қосындысының формуласы
Sn=![]()
І топқа берілетін тапсырма
1) (Аn)-арифметикалық прогрессия
а1= -3 және d =11, а11 мүшесін есептеңдер
а)100; ә)107; в)103; с)105
2) (Аn)- тізбегі арифметикалық прогрессия
а11 = 15, а3= 20 болғандағы d мен а1 ді есептеңдер
а) 5; 10; ә) 5; 5; в) 5; -10; с) -5; 10
3)Арифметикалық прогрессияның а1 мүшесін табыңдар
а15 = 219, d = 14
а) -23; ә) 24; в) 23; с) -24
4) Арифметикалық прогрессияның а9 мүшесін табыңдар
0,2; 1;
а) 6,6; ә) 5; в) 5,6; с) 6
5) Арифметикалық прогрессияның қасиетін пайдаланып қай мүшесін табуға болады және нешеге тең
а4 = 3; а6= 7
а) 5; ә) 6; в) 4; с) 5,5
6) Арифметикалық прогрессияның алғашқы 10 мүшесінің қосындысын есептеңдер
10; 8;
а) 190; ә) -190; в) 10; с) 1; е) -10
ІІ топқа берілетін тапсырма
1) (Аn)-арифметикалық прогрессия
а1= 0,8 және d =-0,2 ; а11 мүшесін табыңдар
а) 1,2; ә) -1,2; в)1,3; с) 1,5
2) (Аn)- тізбегі арифметикалық прогрессия
а3 = -17; а4= 10,5 болғандағы d мен а1 ді табыңдар
а) 6,5; 4; ә) -27,5;72; в) 27,5; -72; с) -6,5;-4
3) Арифметикалық прогрессияның а1 мүшесін табыңдар
а99=989 ; d =-100
а) 10089; ә) -10089; в) -1089; с) 1089
4) Арифметикалық прогрессияның а9 мүшесін табыңдар
1; -1; ...
а) 15; ә) -15; в) 10; с) -10
5) Арифметикалық прогрессияның қасиетін пайдаланып қай мүшесін табуға болады және нешеге тең
а8= -2 және а9= 12
а)-5; ә) -6; в) 5; с) 6
6) Арифметикалық прогрессияның алғашқы бес мүшесінің қосындысын табыңдар а1= -10; d= 2;
а) -28; ә) -70; в) 70; с) -30; е) 39
ІІІ. Үйге тапсырма №5,№6 есептер
ІV. Сабақты қорытындылау
а) Қандай сан тізбегін арифметикалық прогрессия деп атайды?
б) Арифметикалық прогрессияның айырмасы деп қандай санды айтады?
в) Арифметикалық прогрессияның n мүшесінің формуласын жазыңдар.
Сабақ: № 7,8
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Геометриялық прогрессия
Сабақтың мақсаты:
Білімділік: Геометриялық прогрессия тақырыбы бойынша оқушылардың білімдерінің деңгейі мен тиянақтылығын тексеру және бағалау.
Тәрбиелік: ұжымдастыққа. бірізділікке. сыйластыққа тәрбиелеу
Дамытушылық: оқушылардың ойлау қабілеті мен дағдыларын дамыту.
Сабақтың типі: білім мен дағдыны жүйелеу
Сабақтың әдісі: жеке, топтық, деңгейлік
Сабақтың түрі: аралас сабақ
Сабақтың көрнекілігі: оқулық
Сабақтың жүрісі:
І.Ұйымдастыру
II.Геометриялық прогрессия жайында түсініктеме беру:
Бірінші мүшесі b1, екінші мүшесі b2 = b1 · q, үшінші мүшесі b3 = b2 · q ,…, n-ші мүшесі
bn=bn -1 · q болатын сандар тізбегі геометрикалық прогрессия деп аталады.
Мұндағы q -тұрақты сан.
а) 1, 2, 4,… сандар тізбегі геометрикалық прогрессияны құрайды.
Бұнда b1=1, b2=2, b3=4, q=2. Шынымен де b1=1, b2=b1·q=2 · 1=2, b3=b2·q =2 · 2=4.
Бұл прогрессияның жалпы заңдылығы bn=bn-1 · 2.
b). 3, 3/10, 3/100,… сандар тізбегі геометрикалық прогрессияны құрайды.
Бұнда b1=3, b2=3/10, b3=3/100, q=1/10. Шынымен де b1=3, b2=b1 ·q=3 · 1/10=3/10, b3=b2 ·q=3/10· 1/10=3/100.
Бұл прогрессияның жалпы заңдылығы bn=bn-1·1/10.
Геометрикалық прогрессия мүшелерінің қасиеттері:
a). bn2=bn-1·bn+1
b). bn2=bn-k·bn+k , k ≤ n
Sn символымен геометрикалық прогрессияның алғашқы n мүшесінің қосындысын белгілейік.
Яғни Sn=b1+b2+…+bn
Мысалы.
Жоғарыдағы 1, 2, 4,… геометрикалық прогрессия үшін S1=1, S2=1+2=3, S3=1+2+4=7.
Тұжырым.
Sn=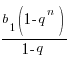
Егер |q|<1 болса онда S=![]() =b1+b2+…+bn+…+
шегі бар болады әрі
=b1+b2+…+bn+…+
шегі бар болады әрі 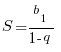
III.Есептер шығару:
№1 тапсырма
1. а) Қандай сан тізбегін арифметикалық прогрессия деп атайды?
Б) Арифметикалық прогрессияның айырмасы деп қандай санды айтады?
В) Арифметикалық прогрессияның n мүшесінің формуласын жаз.
2. (an) арифметикалық прогрессия және a1=3, d=2. S9- неге тең?
3. Геометриялық прогрессияның q=3 және S4 =80 болса, S3-неге тең?
№2 тапсырма
1. а) Қандай сан тізбегін геометриялық прогрессия деп атайды?
Б) Геометриялық прогрессияның еселігі деген не?
В) Геометриялық прогрессияның n мүшесінің формуласын жаз.
2. 1, 4, 7........ арифметикалық прогрессия. Алғашқы 20 мүшесінің қосындысын табыңдар.
3. Геометриялық прогрессияда b4=-54 және b5=162 болса, онда S5-неге тең?
IV.Үйге тапсырма:
№7,№9 .Өтілген тақырыпты оқу
V.Бағалау және қорытындылау
Сабақ: № 9
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Тригонометриялық өрнектер және оларды түрлендіру
Сабақтың мақсаты:
Білімділік: Тригонометриялық өрнектерді түрлендіру және теңбе - теңдіктерді
дәлелдеу тақырыбы бойынша оқушылардың білімдерінің деңгейі мен тиянақтылығын тексеру және бағалау.
Тәрбиелік: ұжымдастыққа. бірізділікке. сыйластыққа тәрбиелеу
Дамытушылық: оқушылардың ойлау қабілеті мен дағдыларын дамыту.
Сабақтың типі: білім мен дағдыны жүйелеу
Сабақтың әдісі: жеке, топтық, деңгейлік
Сабақтың түрі: аралас сабақ
Сабақтың көрнекілігі: оқулық
Сабақтың жүрісі:
І.Ұйымдастыру
ІІ. Қайталау - оқу анасы. Жұп және тақ функцияларды ата? Негізгі тригонометриялық тепе - теңдік. Келтіру формуласы қандай мақсатта қолданылады? Қосу формуласы не үшін қолданылады? sin2α - ? cos2α - ?
ІІІ. Деңгейлік тапсырмалар.
І деңгей: Тепе теңдік орнатылатындай жұлдызшаның (*) орнына тиісті мәнді жазыңдар. 1) tgα* = 1 2)tgα=*/соsα 3) cos(*+α)=sinα 4) sin2α =2*cosα 5) sin(π -*)=sinα 6) sin(α+β)=sinα* + cosα*
Жауабы: 1) tgα ctgα=1 2) tgα= sinα\cosα 3) cos(3π\2+ α) =sinα 4) sin2α=2sinαcosα 5) sin(π - α) = sinα 6) sin(α+β) = sinαcosβ + cosαsinβ
ІІ деңгей: Есептерді шығарып, нәтижесіне сәйкес әріптерді қою керек.
А: 1-cos²α = sin²α
Л: cos²α-1 = -sin²α
Г: (1+tgα)cos²α = 1
Е: (1-cos²α)\(1-sin²α) = tg²α
Б: ctg²αsin²α = cos²α
Р: sin2α\2sinα = cosα
А: (1+cos)(1-cosα) = sin²α
ІІІ деңгей: Өрнектерді ықшамдаңдар: 1) (sinα + cosα)²\ 1 + sin2α 2) 2tgα\ 1 + tg²α 3) ctgα(1-cos2α) 4) (1-tg²α)(1+tg²α) 5) (sin4 α- sin²α)\ (sin²α - cos²α sin²α) 6) sin2α - ctgα
Жауабы: 1) 1; 2) sin2α; 3) sin2α; 4) cos2α; 5) -cosα; 6) tgαcos2α:
ІV. Өзіндік жұмыс.
1) sinα = -4\5 1800 < < 2700 , tgα -?
2)tg1200 -? 3) sin²α (1+ ctgα) + cos²α (1+tgα) - sinα Өрнегін ықшамдаңдар
4) Есептеңдер: 2sin300 - 0 ctg450 tg300 5) Тепе - теңдікті дәлелдеңдер: (tgα + ctgβ )\ (ctgα + tgβ) = tgαctgβ
V. Қорытынды:
1) Ординатаның радиусқа қатынасы қалай аталады? (синус)
2) Жұп функцияны атаңыз? (косинус)
3) Котангенске кері функция? (тангенс)
4) Іргелес жатқан катеттің қарсы жатқан катетке қатынасы қалай аталады? (котангенс)
Синус, косинус, тангенс, котангенс - тригонометриялық функциялар.
VІ. Үйге тапсырма: тест тапсырмаларынан есептер шығару .
№6,№7 есептер
Сабақ: № 10
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Тригонометриялық өрнектер және оларды түрлендіру
Сабақтың мақсаты:
Білімділік: Тригонометриялық өрнектерді түрлендіру және теңбе - теңдіктерді
дәлелдеу тақырыбы бойынша оқушылардың білімдерінің деңгейі мен тиянақтылығын тексеру және бағалау.
Тәрбиелік: ұжымдастыққа. бірізділікке. сыйластыққа тәрбиелеу
Дамытушылық: оқушылардың ойлау қабілеті мен дағдыларын дамыту.
Сабақтың типі: білім мен дағдыны жүйелеу
Сабақтың әдісі: жеке, топтық, деңгейлік
Сабақтың түрі: аралас сабақ
Сабақтың көрнекілігі: оқулық
Сабақтың жүрісі:
І.Ұйымдастыру
ІІ. Қайталау - оқу анасы. Жұп және тақ функцияларды ата? Негізгі тригонометриялық тепе - теңдік. Келтіру формуласы қандай мақсатта қолданылады? Қосу формуласы не үшін қолданылады? sin2α - ? cos2α - ?
ІІІ. Деңгейлік тапсырмалар.
І деңгей: Тепе теңдік орнатылатындай жұлдызшаның (*) орнына тиісті мәнді жазыңдар. 1) tgα* = 1 2)tgα=*/соsα 3) cos(*+α)=sinα 4) sin2α =2*cosα
5) sin(π -*)=sinα 6) sin(α+β)=sinα* + cosα*
Жауабы: 1) tgα ctgα=1 2) tgα= sinα\cosα 3) cos(3π\2+ α) =sinα 4) sin2α=2sinαcosα 5) sin(π - α) = sinα 6) sin(α+β) = sinαcosβ + cosαsinβ
ІІ деңгей: Есептерді шығарып, нәтижесіне сәйкес әріптерді қою керек.= sin²α
Л: cos²α-1 = -sin²α
Г: (1+tgα)cos²α = 1
Е: (1-cos²α)\(1-sin²α) = tg²α
Б: ctg²αsin²α = cos²α
Р: sin2α\2sinα = cosα
А: (1+cos)(1-cosα) = sin²α
ІІІ деңгей: Өрнектерді ықшамдаңдар: 1) (sinα + cosα)²\ 1 + sin2α 2) 2tgα\ 1 + tg²α 3) ctgα(1-cos2α) 4) (1-tg²α)(1+tg²α) 5) (sin4 α- sin²α)\ (sin²α - cos²α sin²α) 6) sin2α - ctgα
Жауабы: 1) 1; 2) sin2α; 3) sin2α; 4) cos2α; 5) -cosα; 6) tgαcos2α:
ІV. Өзіндік жұмыс.
1) sinα = -4\5 1800 < < 2700 , tgα -?
2)tg1200 -? 3) sin²α (1+ ctgα) + cos²α (1+tgα) - sinα Өрнегін ықшамдаңдар
4) Есептеңдер: 2sin300 - 0 ctg450 tg300 5) Тепе - теңдікті дәлелдеңдер: (tgα + ctgβ )\ (ctgα + tgβ) = tgαctgβ
V. Қорытынды:
1) Ординатаның радиусқа қатынасы қалай аталады? (синус)
2) Жұп функцияны атаңыз? (косинус)
3) Котангенске кері функция? (тангенс)
4) Іргелес жатқан катеттің қарсы жатқан катетке қатынасы қалай аталады? (котангенс)
Синус, косинус, тангенс, котангенс - тригонометриялық функциялар.
VІ. Үйге тапсырма: тест тапсырмаларынан есептер шығару .
№10,№11 есептер 7-нұсқа
Сабақ: № 11-13
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Тригонометриялық теңдеулер
Сабақтың мақсаты:
Білімділік: Тригонометриялық теңдеулерді шешу тақырыбы бойынша оқушылардың білімдерінің деңгейі мен тиянақтылығын тексеру және бағалау.
Тәрбиелік: ұжымдастыққа, бірізділікке. сыйластыққа тәрбиелеу
Дамытушылық: оқушылардың ойлау қабілеті мен дағдыларын дамыту.
Сабақтың типі: білім мен дағдыны жүйелеу
Сабақтың әдісі: жеке, топтық, деңгейлік
Сабақтың түрі: аралас сабақ
Сабақтың көрнекілігі: оқулық
Сабақтың жүрісі:
І.Ұйымдастыру
ІІ. Жаңа білімді меңгерту
Анықтама: sin x=a, cos x=a, tg x=a, ctg x=a түрінде берілген теңдеулерді қарапайым тригонометриялық теңдеулер деп атайды.
Есептер шығару:
№1.![]()
![]()
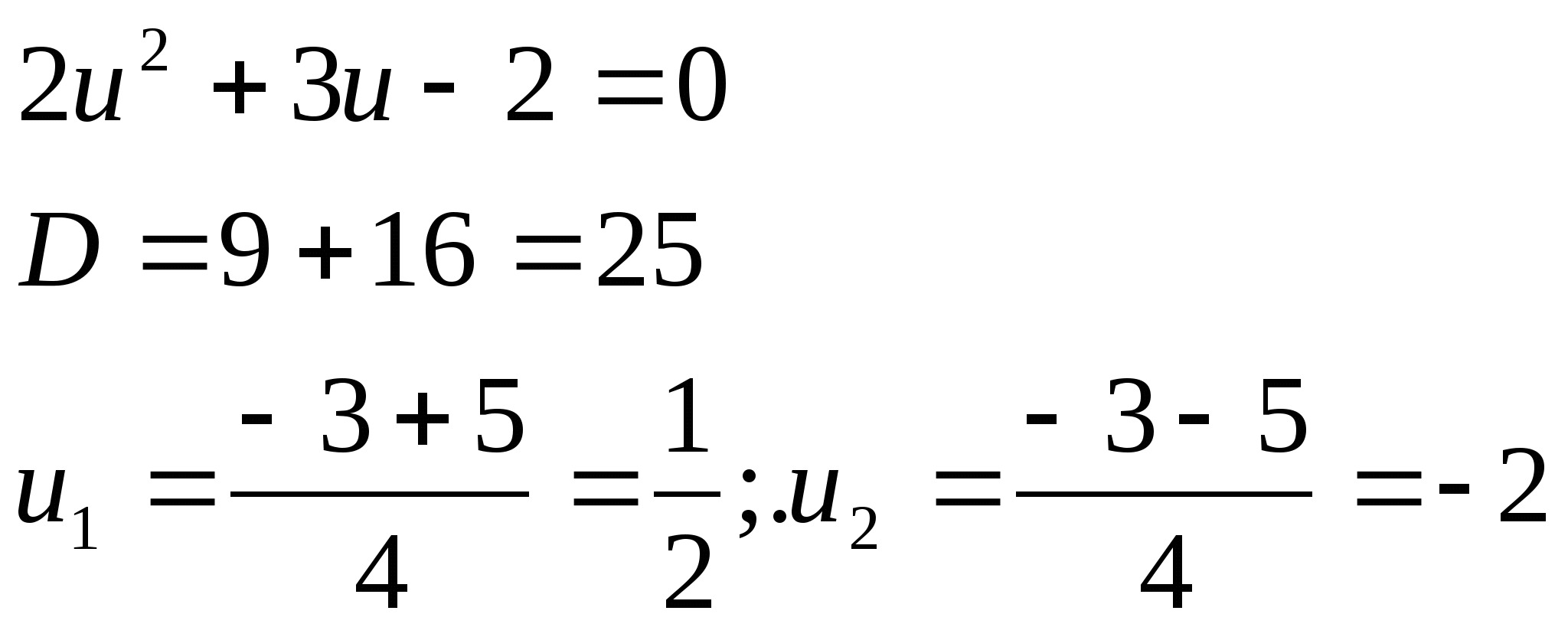
![]() шешімі
жоқ |-2|>1
шешімі
жоқ |-2|>1 ![]()
![]() nϵZ
nϵZ
№2. ![]()
![]() бойынша
бойынша
![]()
![]()
![]()
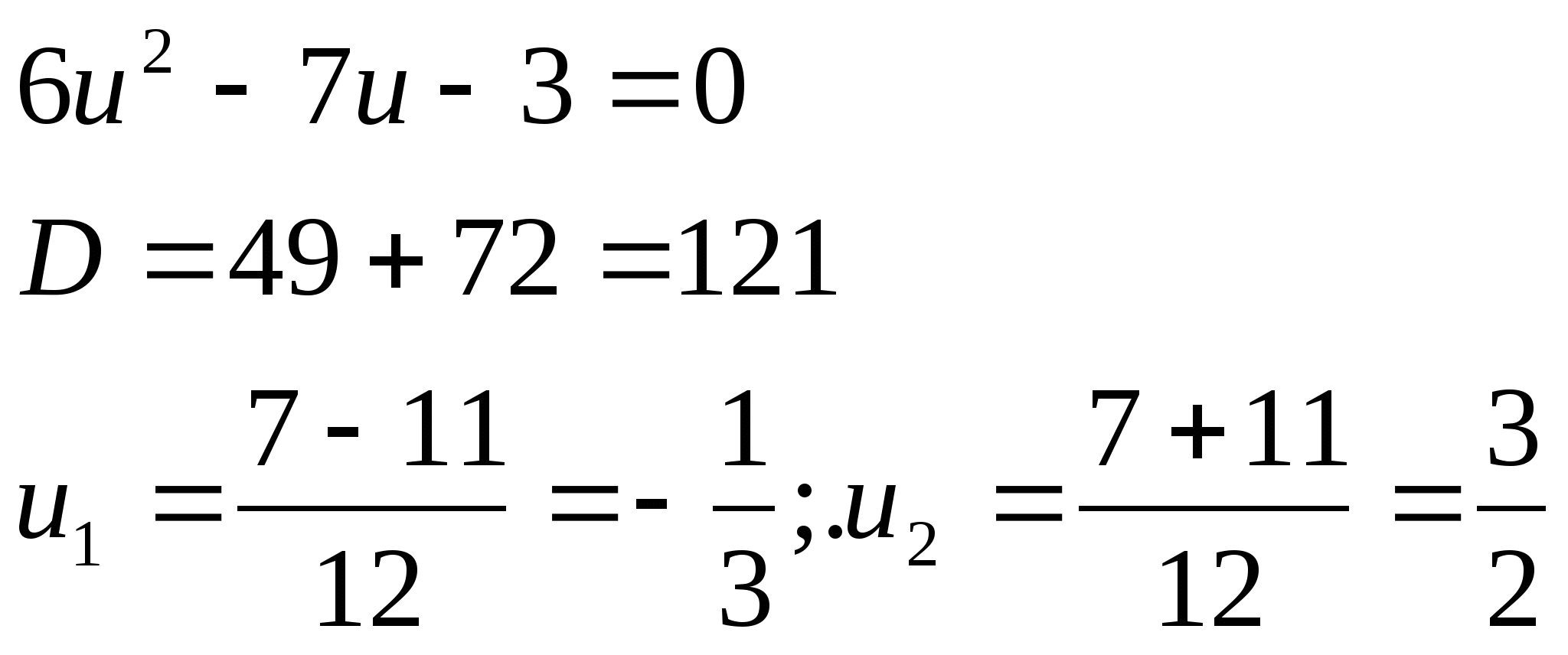
|![]() |>1
|>1
![]()
![]() nϵZ
nϵZ
№3. ![]()
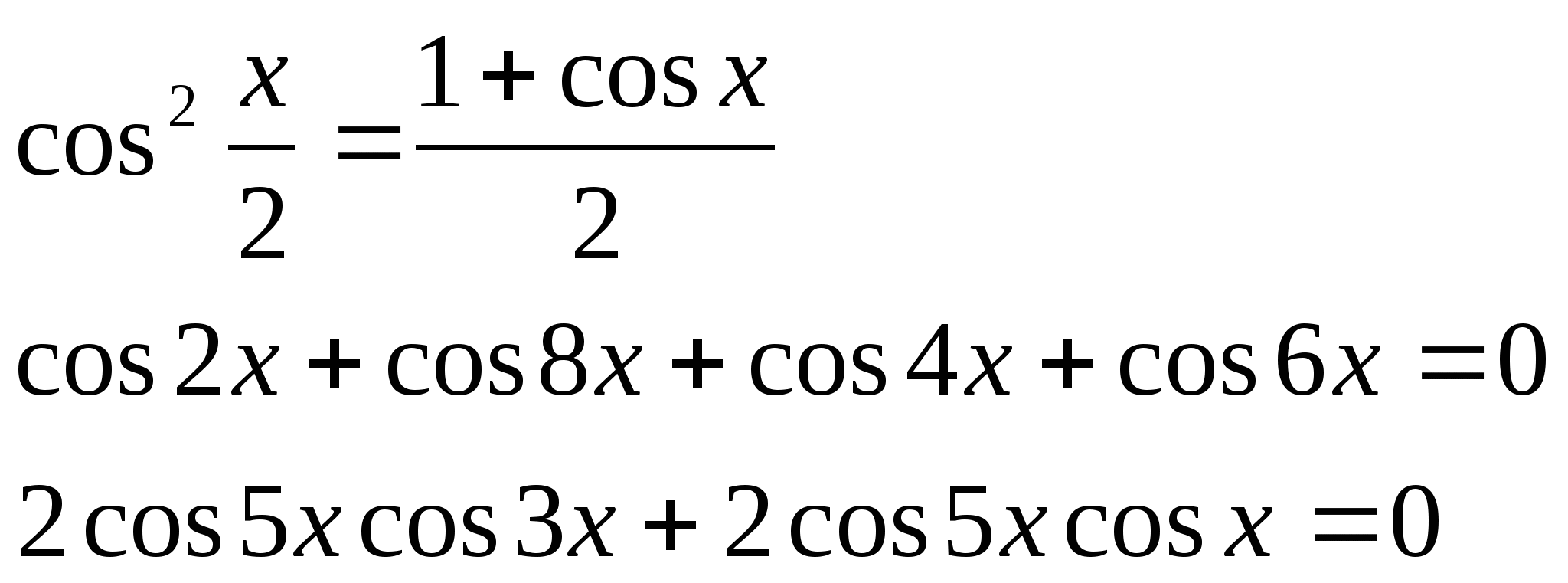
![]()
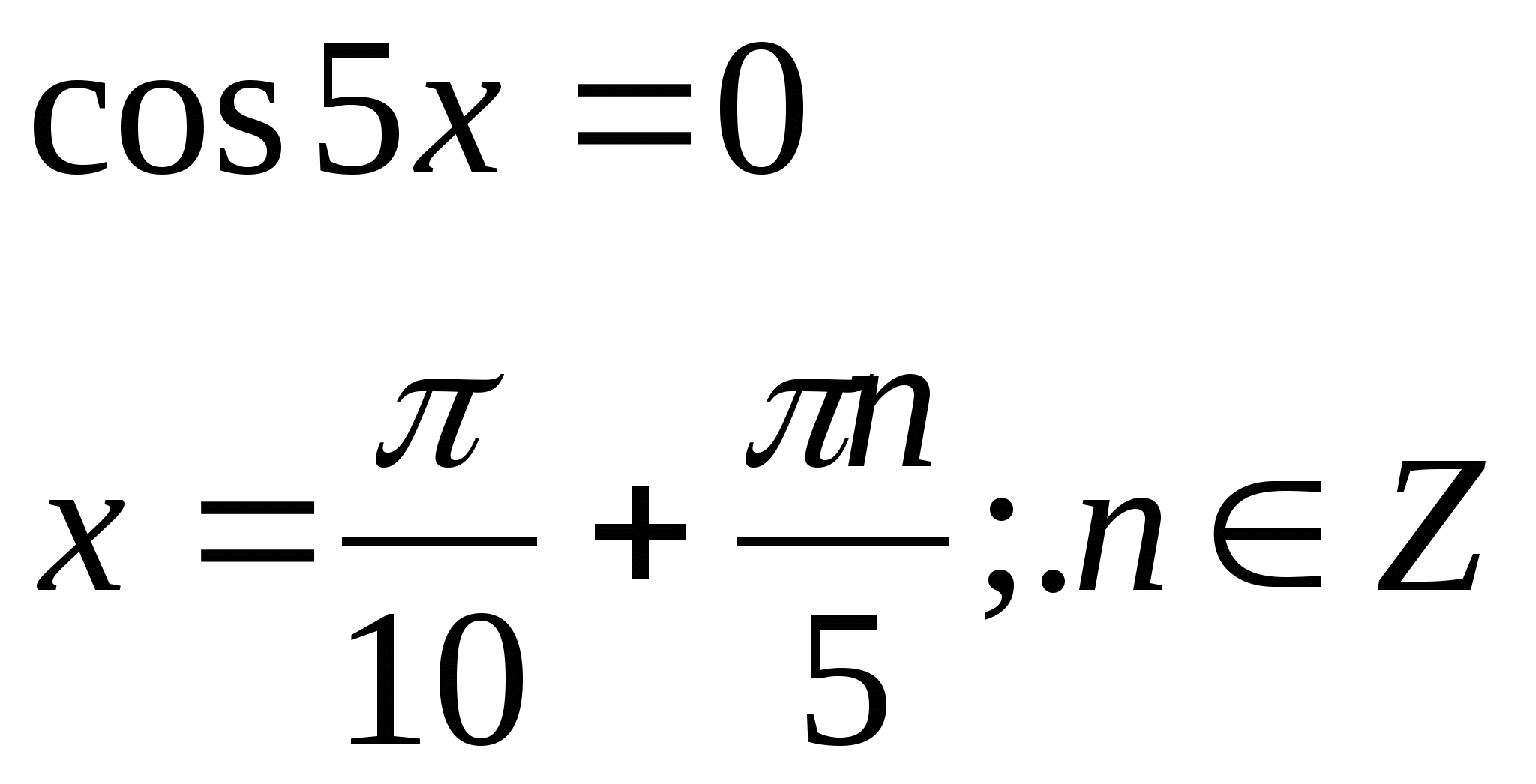
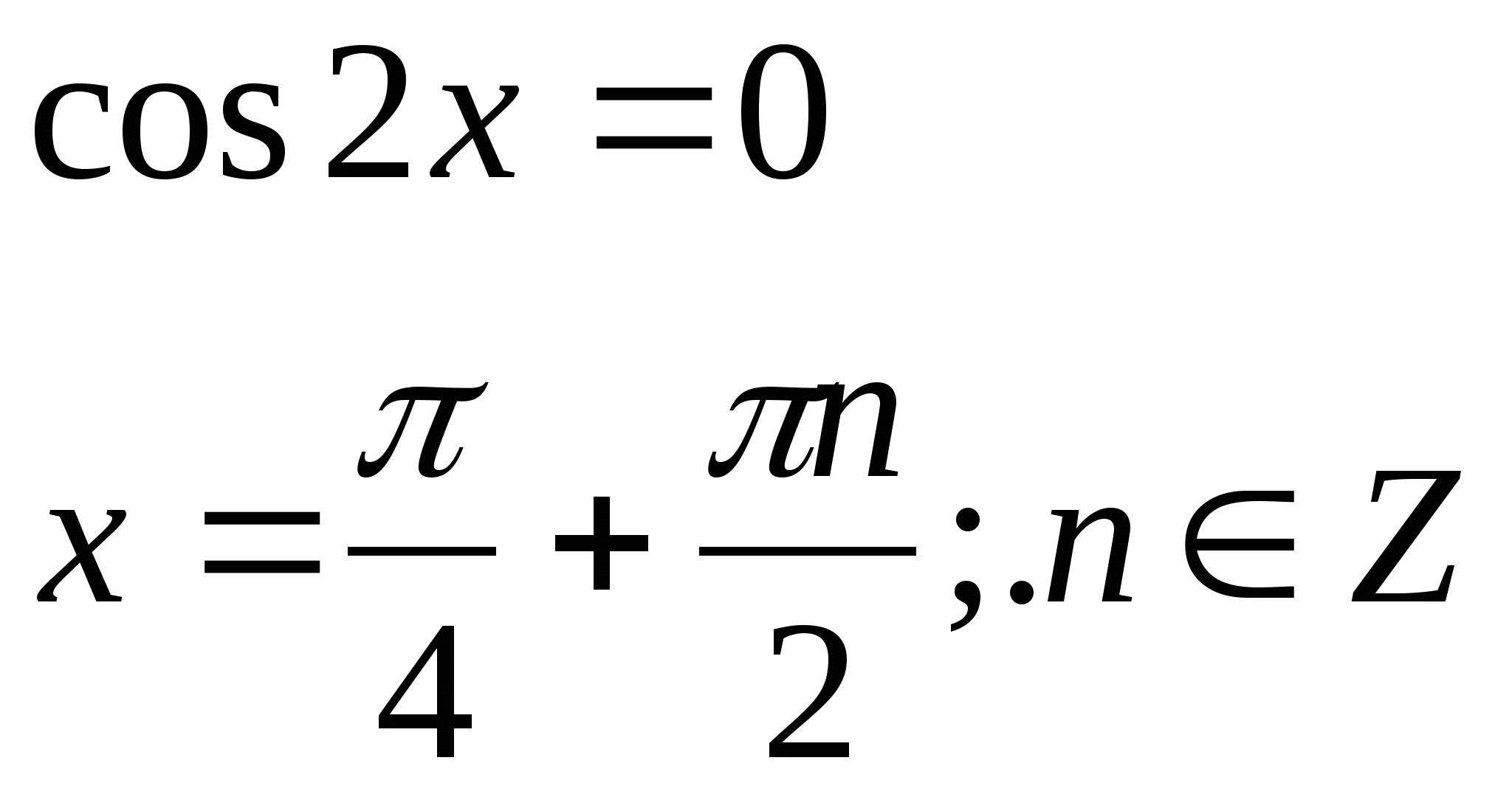
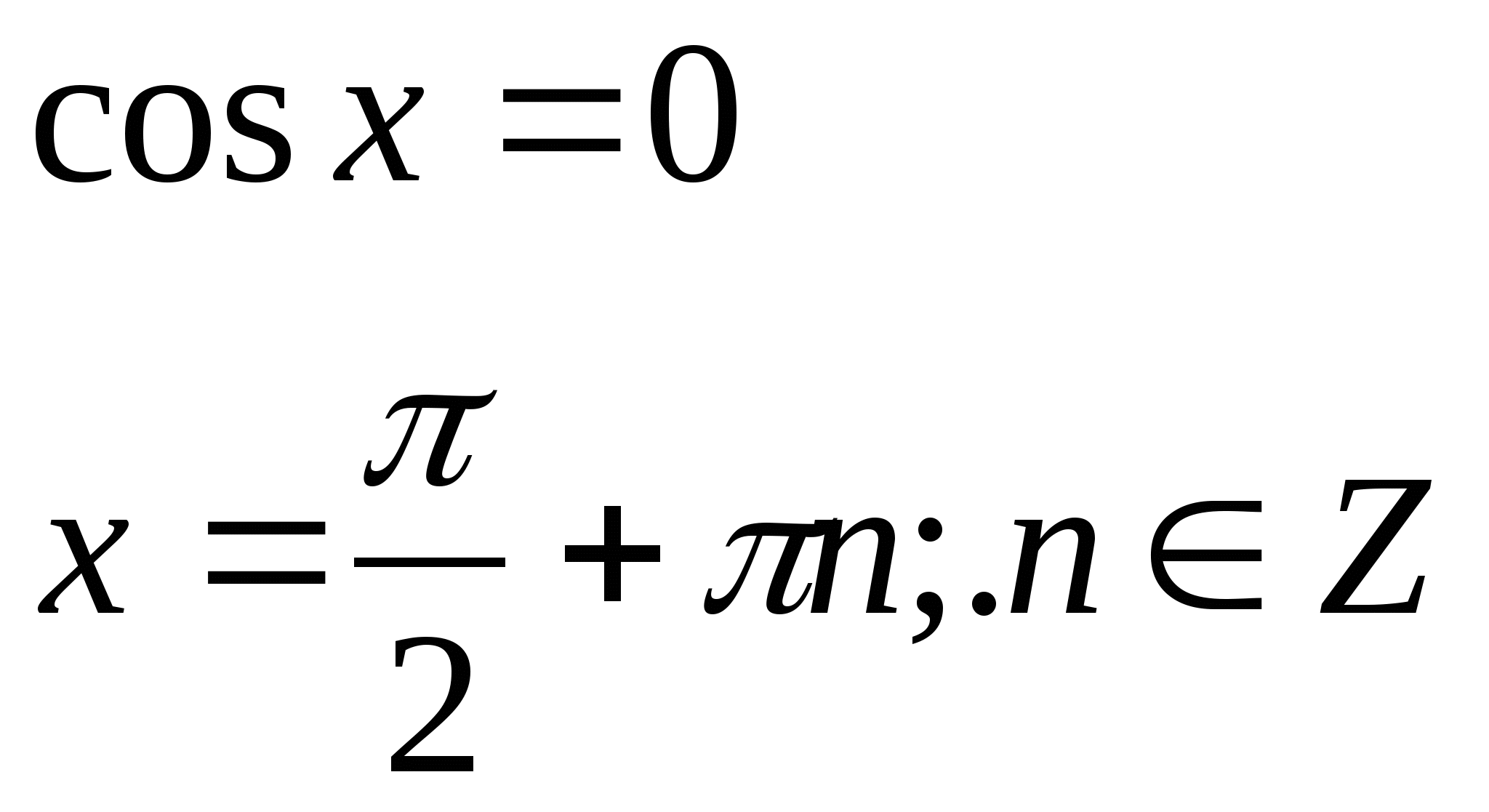
№4. ![]()
![]()
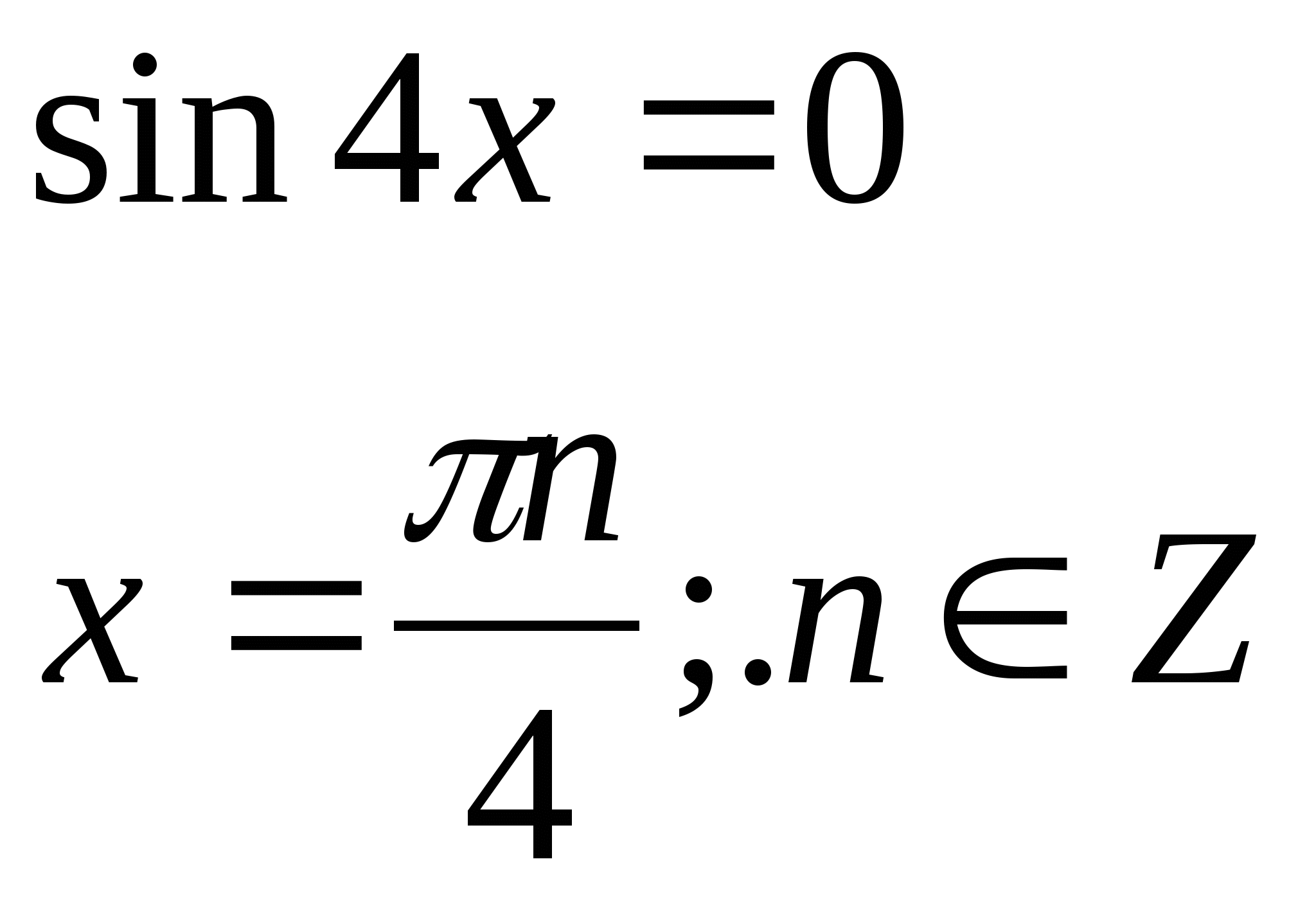
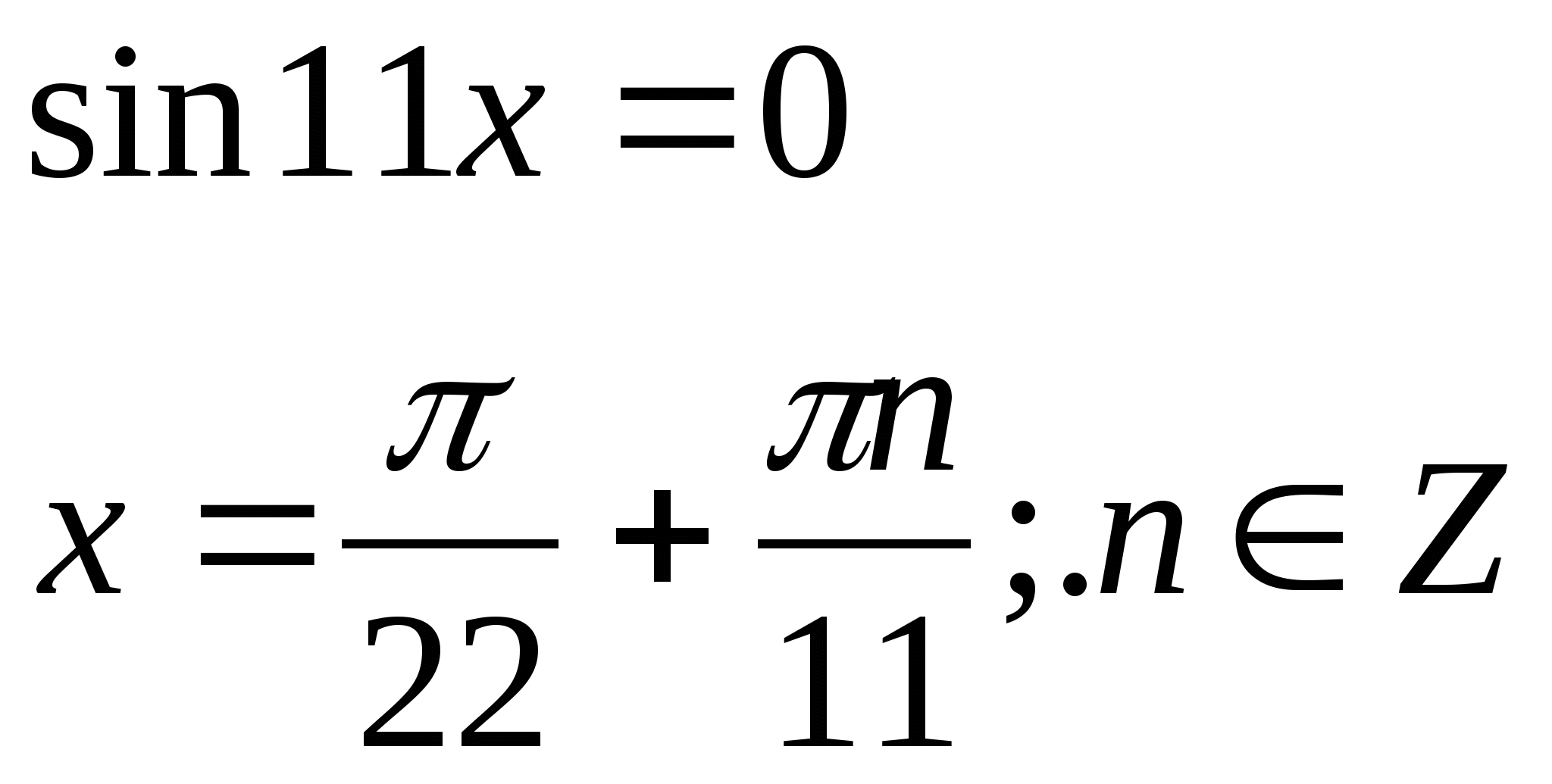
№5 .![]()
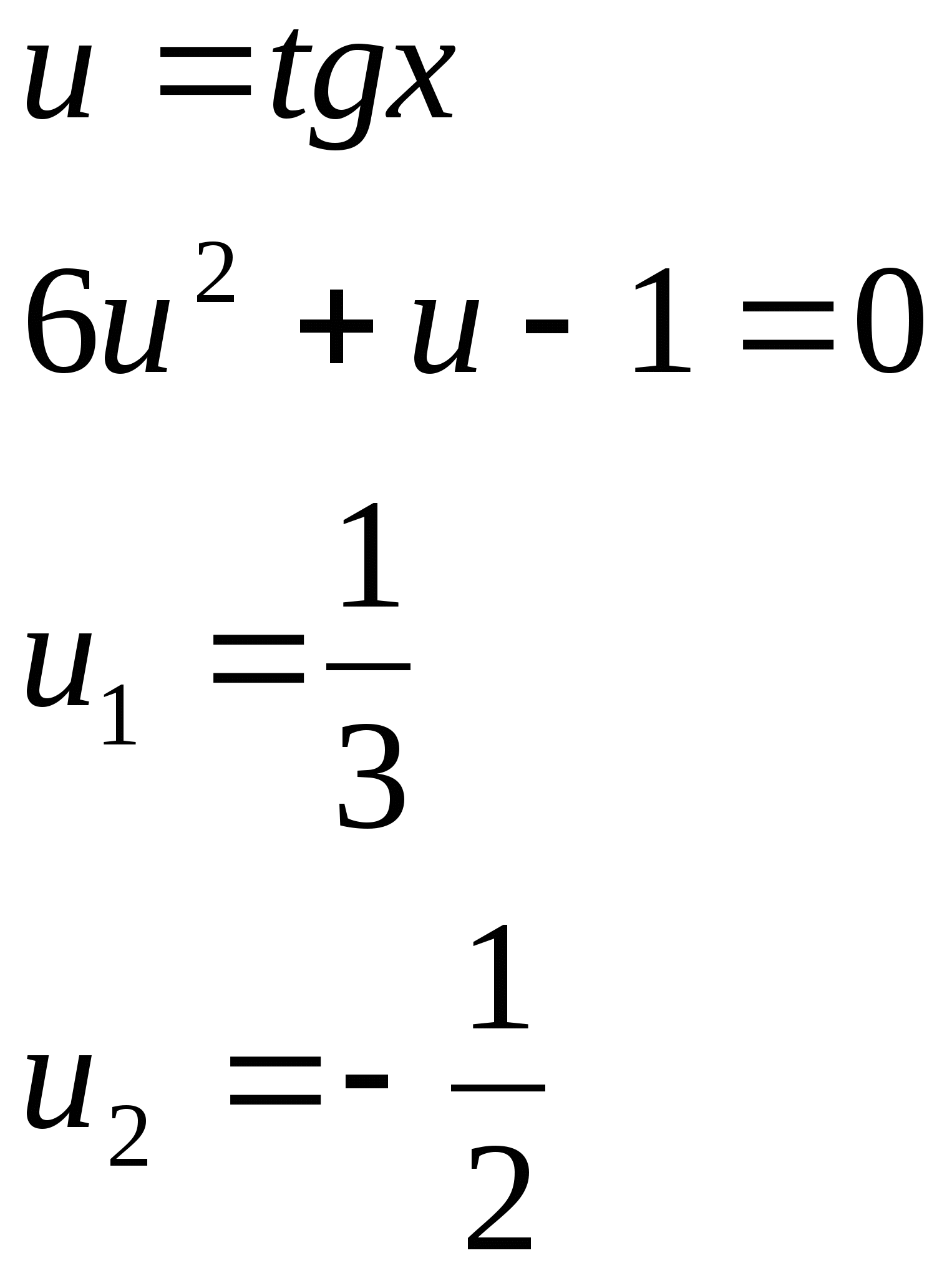
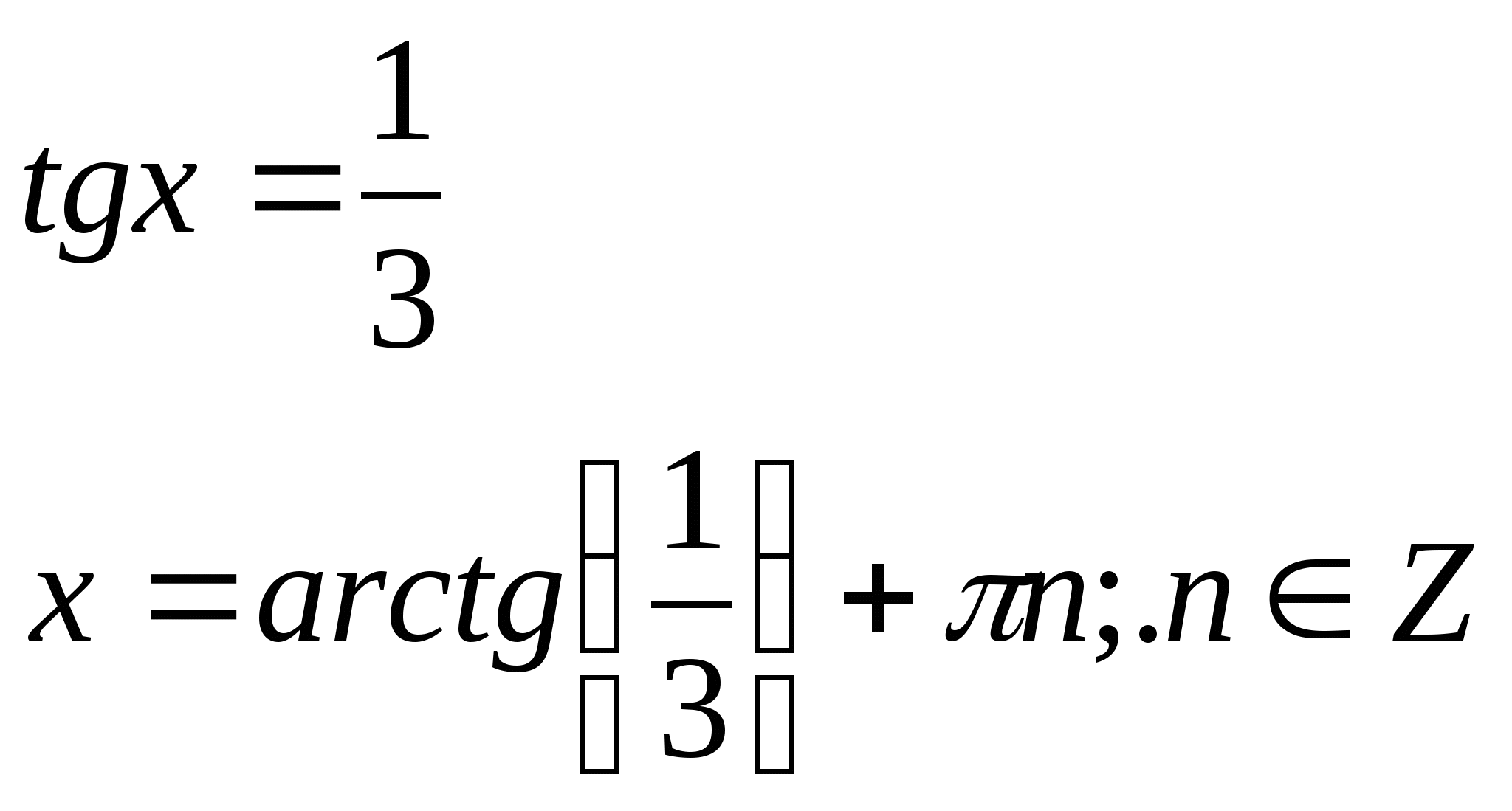
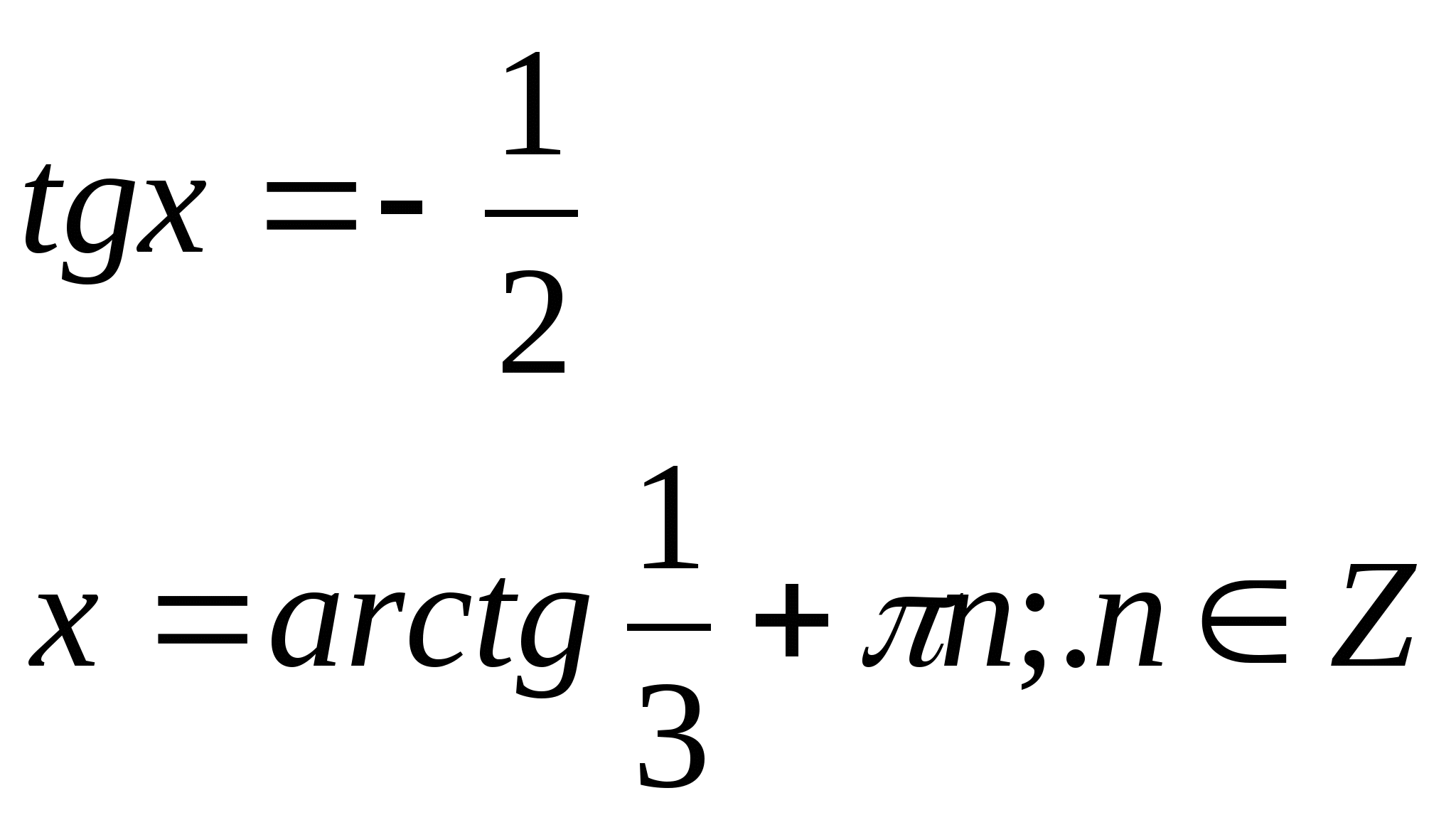
№6. ![]()
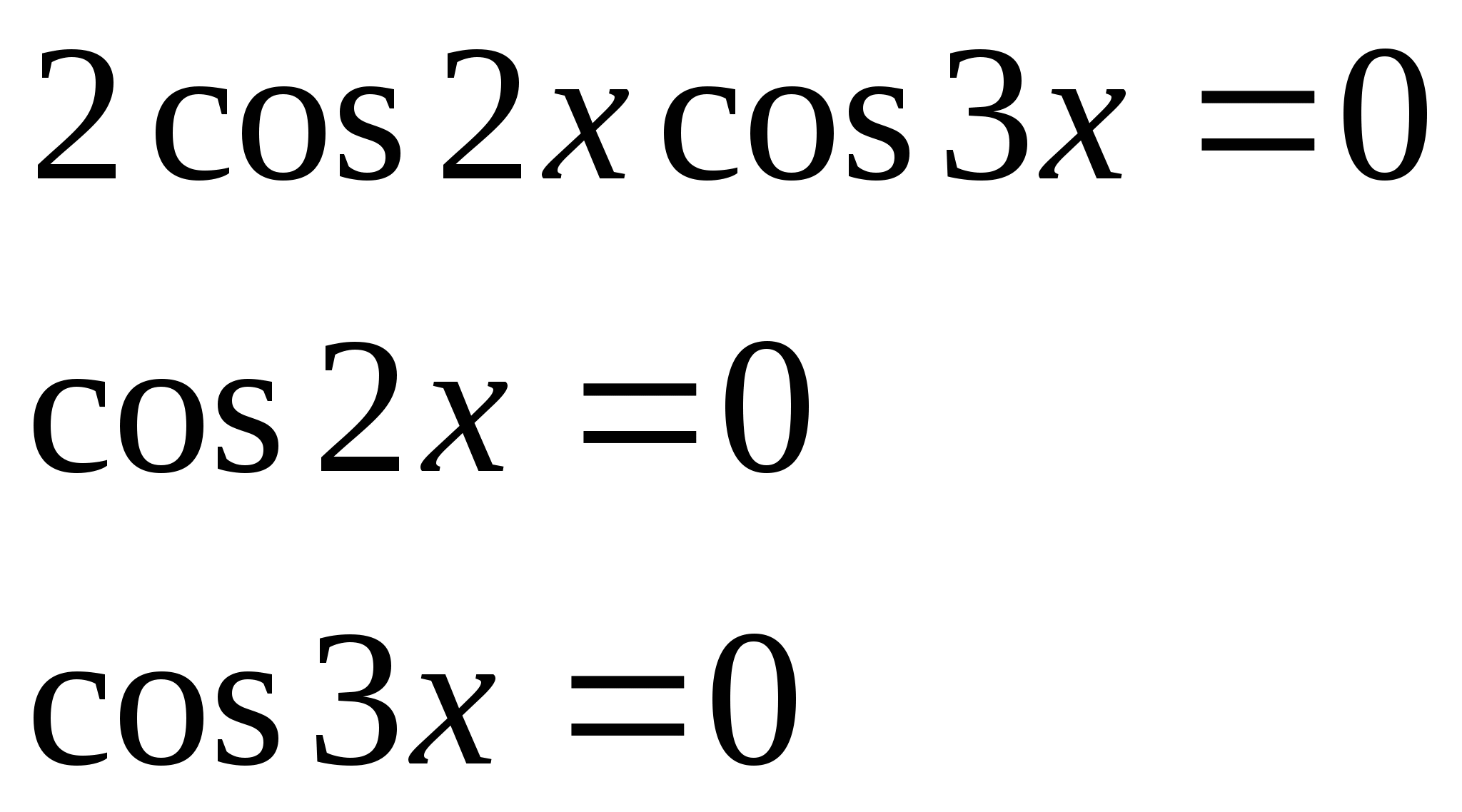
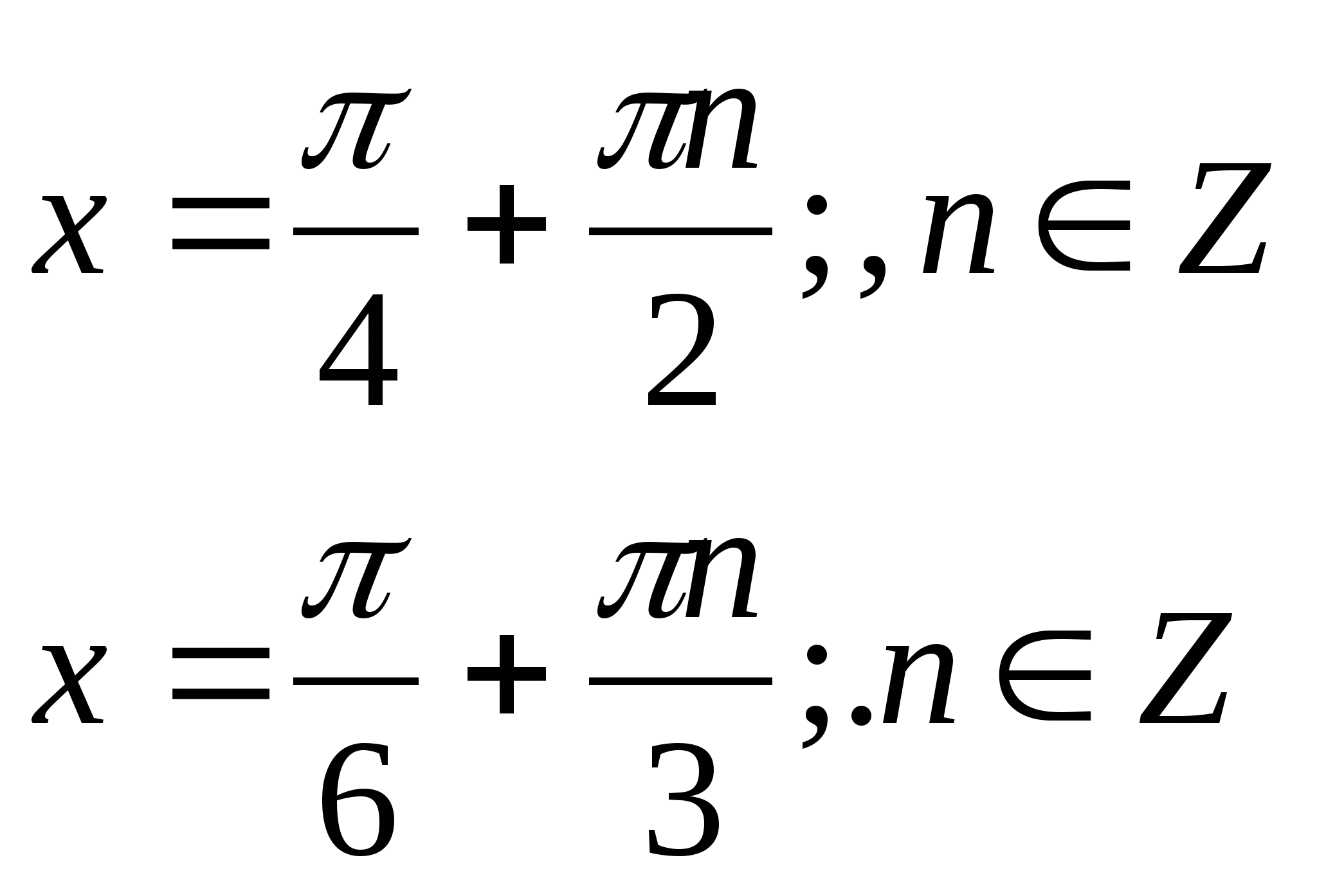
№7. ![]()
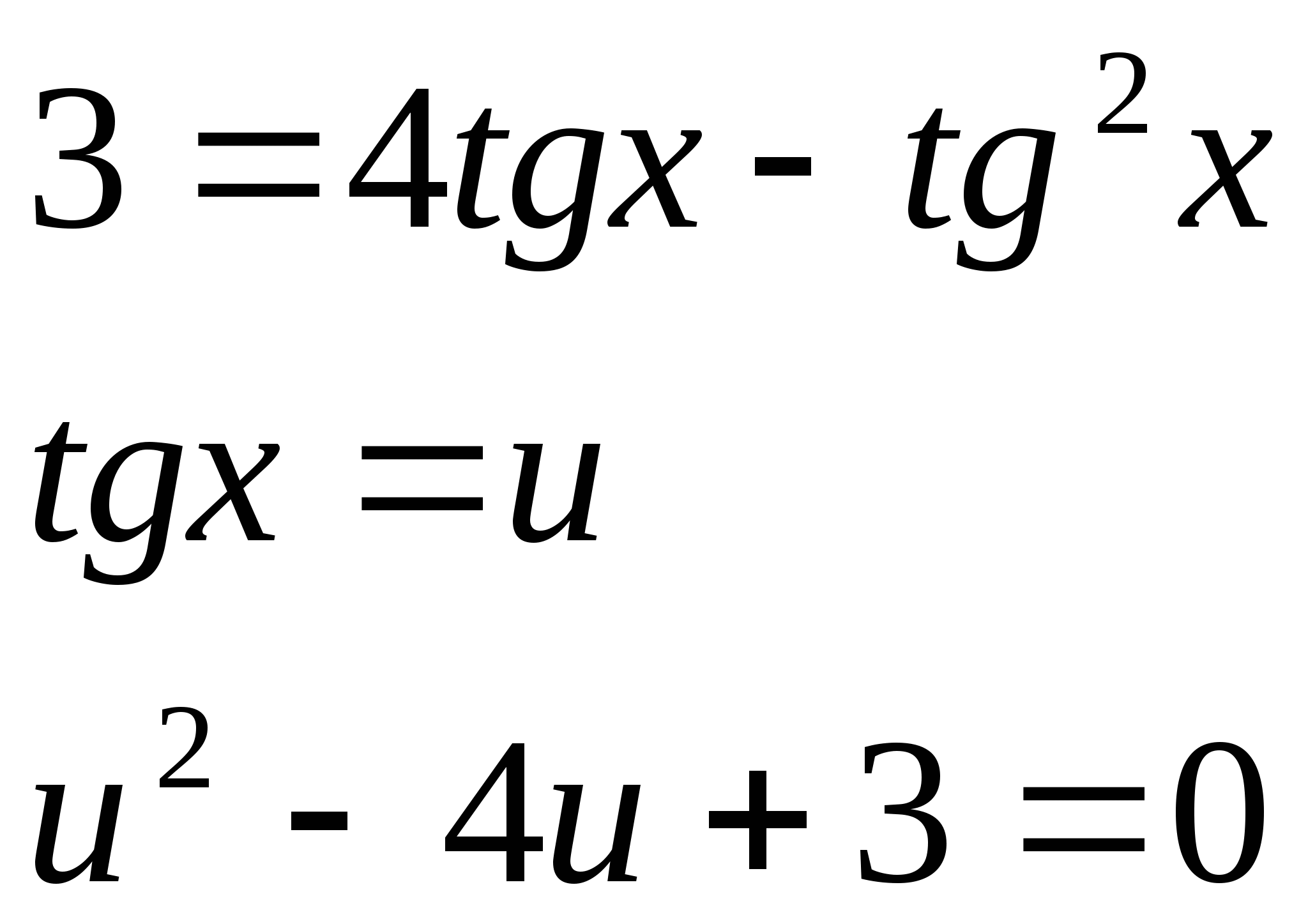
![]()
![]()
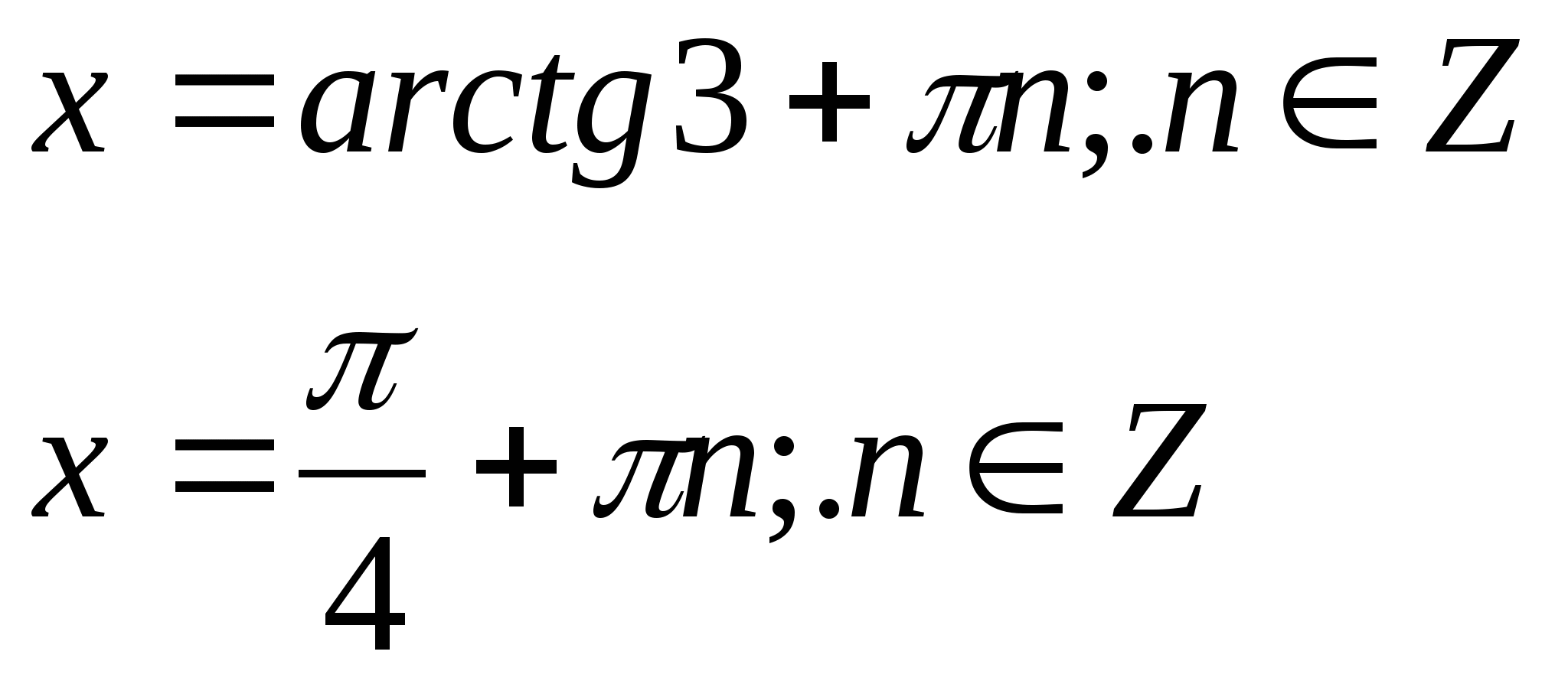 1.Теңдеулерді
шешіңдер:
1.Теңдеулерді
шешіңдер:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]() 5)
5) ![]() .
.
№8.
|
Нұсқа 1 |
Нұсқа 2 |
1 |
2 |
3 |
4 |
|
Sinx = -1∕2 |
Sinx = 1∕2 |
х = (-1)пπ∕6+πn |
х = 2πn |
х = (-1)п+1π∕6+πn |
х = +/- 2π∕3+ 2πn |
|
√3tgx-1=0 |
tg 2x-√3=0 |
х = π∕6+πn |
Шешімі жоқ |
х = +/- π∕3+ 2πn |
х = 5π∕6+2πn |
|
Sin(х-π∕3) = 1 |
Sin(х-π∕3) = -1 |
х = -5π∕6+2πn |
х = -π ∕6+2πn |
х =πn |
х = 5π∕6+2πn |
Үйге тапсырма беру: №10,№12
Қорытындылау:
1.Негізгі тригонометриялық функциялар қалай аталады?
2.Тригонометриялық функцияның негізгі қасиеттері қандай?
Сабақ: № 14-16
Бекітемін:
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Логарифмдік функциялар
Сабақтың мақсаты:
Білімділік: Оқушыларға логарифмдік теңдеулерді қалай шешу керектігі жайында мағлұмат беріп,квадрат теңсіздіктерді шешу тәсілдерін үйрету.
Дамытушылық: Оқушылардың шығармашылық ойлау қабілеттерін, танымдық белсенділіктерін арттыру.
Тәрбиелік: Әр оқушының өздігінен еңбектенуге, шапшаңдыққа, дәлдікке тәрбиелеу.
Сабақтың түрі: Аралас сабақ
Сабақтың әдісі: есептер шығару,сұраққа - жауап алу
Сабақтың көрнекілігі: тест тапсырмалары,оқулық
Сабақтың барысы:
І. Ұйымдастыру кезеңі
Оқушыларды түгендеп, сабақтың мақсатымен таныстыру.
2.Есептер шығару:
-
Теңдеуді шешіңіз:

Жауабы: -7
-
Теңдеуді шешіңіз:

Жауабы: 1
-
Теңдеуді шешіңіз:

Жауабы: ![]()
-
Теңдеуді шешіңіз:

Жауабы: -6
-
Теңдеуді шешіңіз:

Жауабы: 12
-
Теңдеуді шешіңіз:

Жауабы: 90
-
Теңдеуді шешіңіз:

Жауабы: 8
-
Теңдеуді шешіңіз:

Жауабы: -3; 1
-
Теңдеуді шешіңіз:

Жауабы: ![]()
-
Теңдеуді шешіңіз:

Жауабы: ![]()
-
Теңдеуді шешіңіз:

Жауабы: 1
-
Теңдеуді шешіңіз:

Жауабы: 1,5
-
Теңдеуді шешіңіз:

Жауабы: log23
-
Теңдеуді шешіңіз:

Жауабы: 4
-
Теңдеуді шешіңіз:

Жауабы: 0,01:100
16.Теңдеуді шешіңіз:![]()
Жауабы: 0,508
17.Теңдеуді шешіңіз:![]()
Жауабы: 6
18.Теңдеуді шешіңіз:![]()
Жауабы: -2
19.Теңдеуді шешіңіз:![]()
Жауабы: 2
20.Теңдеуді шешіңіз:![]()
Жауабы: 13
21.Теңдеуді шешіңіз:![]()
Жауабы: ![]()
22.Теңдеуді шешіңіз:![]()
Жауабы: 5
23.Теңдеуді шешіңіз:![]()
Жауабы: 1
24.Теңдеуді шешіңіз: ![]()
Жауабы: 64
25.Теңдеуді шешіңіз:![]()
Жауабы: 0,1; 1000
Үйге тапсырма: №10,№15
V. Қорытындылау:
Квадрат теңсіздік дегеніміз не?
Квадрат теңсіздіктерді шешу жолдары қандай?
Логарифмдік теңдеулерді қалай шешеді?
Бекітемін:
Сабақ: № 17-19
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Көрсеткіштік функциялар
Сабақтың мақсаты:
Білімділік: Оқушыларға көрсеткіштік теңдеулерді қалай шешу керектігі жайында мағлұмат беріп,квадрат теңсіздіктерді шешу тәсілдерін үйрету.
Дамытушылық: Оқушылардың шығармашылық ойлау қабілеттерін, танымдық белсенділіктерін арттыру.
Тәрбиелік: Әр оқушының өздігінен еңбектенуге, шапшаңдыққа, дәлдікке тәрбиелеу.
Сабақтың түрі: Аралас сабақ
Сабақтың әдісі: есептер шығару,сұраққа - жауап алу
Сабақтың көрнекілігі: тест тапсырмалары,оқулық
Сабақтың барысы:
І. Ұйымдастыру кезеңі
Оқушыларды түгендеп, сабақтың мақсатымен таныстыру.
2.Есептер шығару:
-
«Сәйкестікті тап» ойыны 27х=
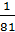
4х=16
![]() х=4
х=4
32х=16
5х+1=125
Жауаптары:х=![]() , x=2, x=4, x=
, x=2, x=4, x=![]() , x=2
, x=2
-
Деңгейлік тапсырмалар:
А деңгейі
3x + 3x+1 = 12
В деңгейі
44х - 2x -2 = 42х-3
С деңгейі
8x + 3∙4x = 12+2x+2
А деңгейі
7x+2 -7x = 336
В деңгейі
6х+1![]() =216
=216
С деңгейі
31+3х-9х=3х+2-3
3)Тест тапсырмалары:
I нұсқа
-
9x - 4∙3x -45=0
-
5 B) 2 C) -5 D) 9 E) 7
-
5x+1 + 2∙5x = 175
-
1 B)
 C) 0 D) 4 E) 2
C) 0 D) 4 E) 2
-
4x - 10∙2x-1 - 24 = 0
-
3,8 B) -3,8 C) 8 D) -3;3 E) 3
-
8x-3 = 9x-3
-
4 B) 3 C) 2 D) 1
-
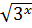 ∙
∙ 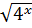 = 36
= 36
-
2 B) 4 C) 1 D) -1
-
5x-1 + 5x-2 + 5x-3 = 155
-
0 B) 2 C) 625 D) 1,24 E) 4
А)![]() ;
;![]() B)
-2;-1 C) 2;2 D) -3;3 E) (-1;1)
B)
-2;-1 C) 2;2 D) -3;3 E) (-1;1)
IIнұсқа
-
121x -2∙11x +1 = 0
-
2 B) 3 C) 1 D) 0 E) 6
-
2x+4 + 3∙2x = 76
-
2 B) 4 C) 3,5 D) 4,5 E) 3
-
4x + 2x+1 - 24 = 0
-
-2;6 B) 2 C) 2;-6 D) -4;6 E) 4;-6
-
2x-4 = 5x-4
-
4 B) 3 C) 2 D)1
-
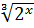 ∙
∙ 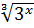 = 216
= 216
-
3 B) 9 C) 1 D) 0
-
3x + 3x+1 +3x+2 +3x+3 = 360
-
2 B) -2 C) 4 D) 1 E)3
7.![]()
-
2;6 B) -0,5 C) -1 D) 1 E) 0,5
Сабақты қорытындылау
Үйге тапсырма :№ 10-№12
Бекітемін:
Сабақ: № 20-22
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Туынды және оның қолданылуы
Сабақтың мақсаты:
Білімділік: Функцияның нүктедегі шегі,туынды тақырыптары бойынша оқушылардың білімдерінің деңгейі мен тиянақтылығын тексеру және бағалау,есептер шығару
Тәрбиелік: ұжымдастыққа, бірізділікке,сыйластыққа тәрбиелеу
Дамытушылық: оқушылардың ойлау қабілеті мен дағдыларын дамыту.
Сабақтың типі: білім мен дағдыны жүйелеу
Сабақтың әдісі: жеке, топтық, деңгейлік
Сабақтың түрі: аралас сабақ
Сабақтың көрнекілігі: оқулық
Сабақтың жүрісі:
1.Ұйымдастыру
2.Жаңа сабақты түсіндіру:
x саны x0 санына ұмтыла берсін, бірақ оған тең болмасын. Бұны x→x0 деп белгілейміз.
Мысалы мына сандар тізбегінің n-ші мүшесі, n өскен сайын нөлге ұмтылады (бірақ нөлге тең болмайды):
![]() ,…
,…
Аңықтама.
A саны y=f(x) функциясының x→x0 ұмтылғандағы шегі деп аталады, егер x0 санына ұмтылған кез келген x1, x2, x3,… сандар тізбегі үшін сәйкесінше f(x1), f(x2), f(x3),… сандар тізбегі A санына ұмтылса.
Бұны 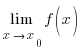 = A деп белгілейді.
= A деп белгілейді.
-
Анықтама:
![]() айырымдылық
қатынастың аргумент өсімшесі
айырымдылық
қатынастың аргумент өсімшесі ![]() нөлге ұмтылғандағы шегі бар болса, онда ол шекті y= f(x)
функциясының х нүктесіндегі өсімшесі деп атайды.
нөлге ұмтылғандағы шегі бар болса, онда ол шекті y= f(x)
функциясының х нүктесіндегі өсімшесі деп атайды.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(cos x)'=-sin x;
(sin x)'= cos x ;
(ctgx)'= 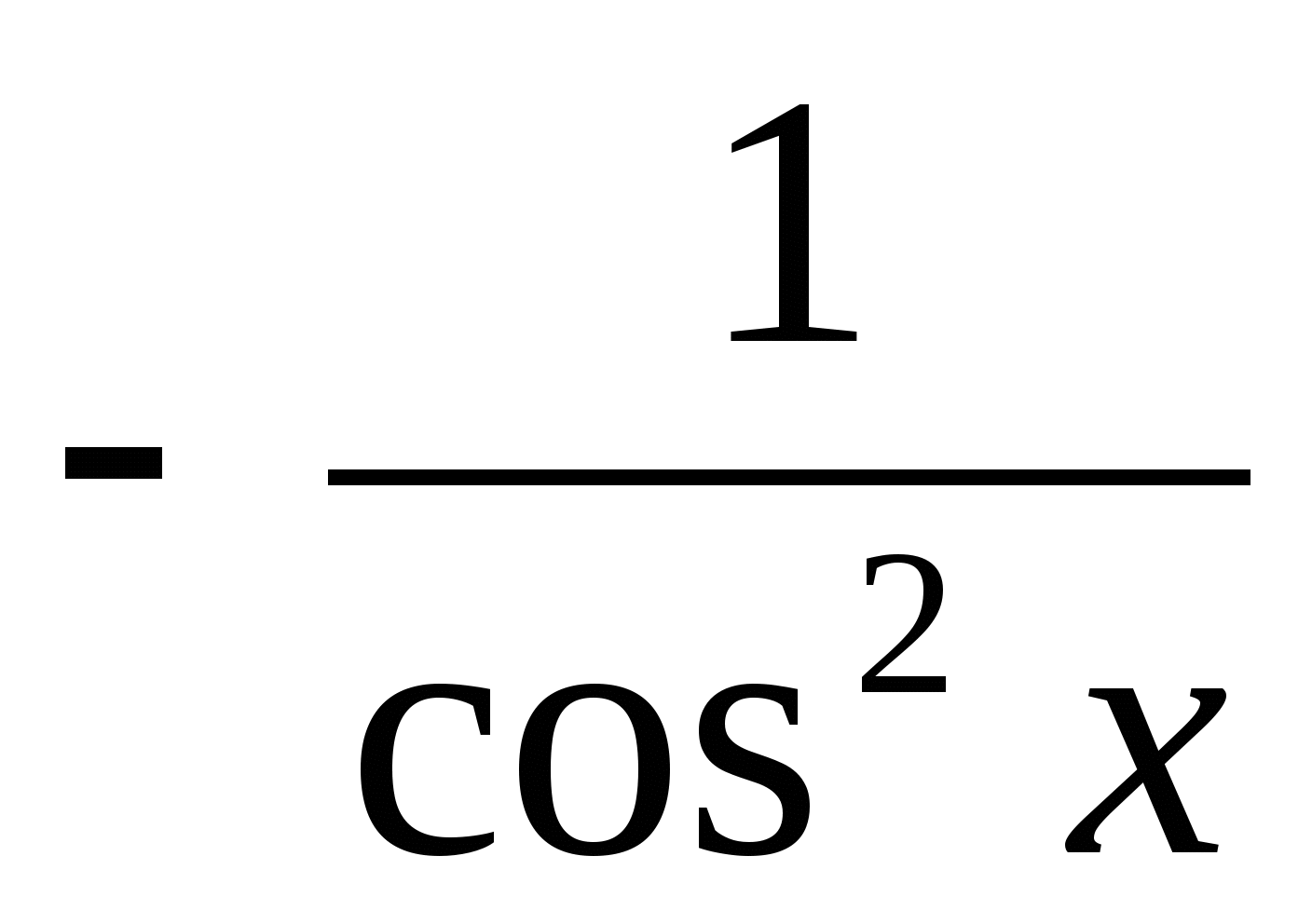
(tg x)'= ![]()
3.Есептер шығару: №1
-
Тапсырма: f'(x) функциясының туындысын тап, егер:
а) f(x)= x![]() в) f(x)=2,5x
в) f(x)=2,5x![]()
б) f(x)=![]() г) f(x)=5x
г) f(x)=5x![]()
Шешімі:
а) f(x)= x![]()
Туындыны есептеу формулаларын қолдана отырып келесідей есептеулерді аламыз:
f'(x)= (x![]()
б) f(x)=![]()
f'(x)= ![]()
в) f(x)=2,5x![]()
![]() болғандықтан
болғандықтан
f'(x)= 2,5(х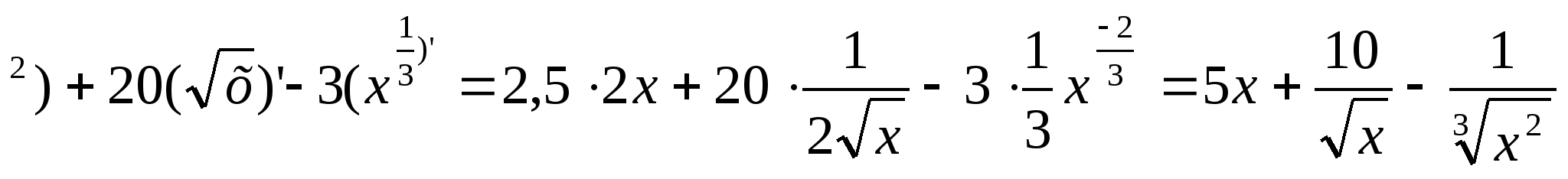
г) f(x)=5x![]()
5x![]() (
(![]() -
const, екендігін біле отырып, мынандай шешімдерін аламыз:
-
const, екендігін біле отырып, мынандай шешімдерін аламыз:
f'(x)= 5(х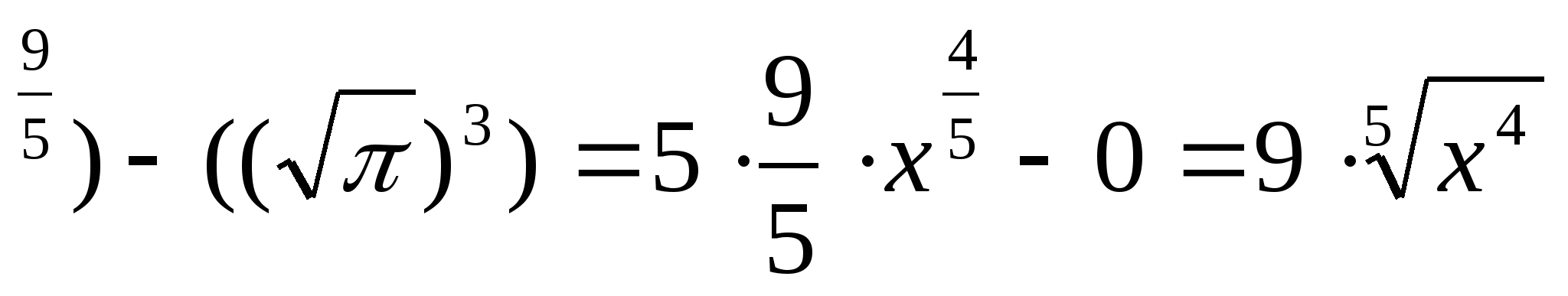
№2 Функцияның туындысын табыңдар:
а) f(х) = (х2 + )9
ә) f(х) = (х5 - )11
Үйге тапсырма: №20-№25 5 нұсқа 2014 ж тест
Бағалау және қорытындылау
Сабақ: № 23-25
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Алғашқы функция
Сабақтың мақсаты:
1. Білімділігі:Алғашқы функцияның негізгі қасиеті және алғашқы функцияны табудың ережелерін пайдаланып есептер шығару. Алғашқы функцияны және анықталмаған интегралды табу бойынша білім, білік, дағдыларын бекіту.
2. Дамытушылық: Логикалық ойлау қабілеті мен есептеу дағдыларын жетілдіру, өз бетінше еңбектену, белсенділіктерін арттыру, пәнге қызуғушылығын ояту, оқушылардыңқұзыреттерін қалыптастыру.
3.Тәрбиелік: Оқушылардыңөз ойын толық, дұрыс жеткізе білуге, тапқырлыққа, жылдамдылыққа, ептілікке, достыққарым-қатынасқа тәрбиелеу.
Сабақтың типі: білім мен дағдыны жүйелеу
Сабақтың әдісі: жеке, топтық, деңгейлік
Сабақтың түрі: аралас сабақ
Сабақтың көрнекілігі: оқулық
Сабақтың жүрісі:
1.Ұйымдастыру
2.Жаңа сабақты түсіндіру:
Анықтама:
Үзіліссіз, y=f(x), f(x)>0 функциясының графигімен, абсцисса осімен және x=a. x=b түзулерімен шектелген жазық фигура қисықсызықты трапеция деп аталады.
Ә) Қисықсызықты трапецияның ауданын есептеу формуласын қорытып шығару. (S=F(b)-F(a))
Б) Қисықсызықты трапецияның табанымен таныстыру. (қисықсызықты трапецияның табаны ретінде алынатын [a;b] кесіндісі)
В) Қисықсызықты трапецияның ауданын есептейтін алгоритімен таныстыру.
1. Бір координаталық жазықтықта берілген қисықтардың графиктерін салу;
2.Графигі жоғарыдан қисықсызықты трапецияны шектейтін функцияның алғашқы функцияларының бірін анықтау;
3.Қисықсызықты трапецияның төменгі табаны болатын кесіндінің шеткі нүктелерінің координаталарын анықтау;
4. S=F(b)-F(a) формуласы бойынша қисықсызықты трапецияның ауданын есептеу
Формулалармен таныстыру
3.Есептер шығару:Берілген қисықтармен шектелген фигураның ауданын табыңдар:
1. y=![]() және у=6х-х2 сызықмен шектелген фигураның ауданы неге
тең?
және у=6х-х2 сызықмен шектелген фигураның ауданы неге
тең?
2.y=x3,y=0,x=1,x=2 сызықтармен шектелген аудан неге тең?
3.y=sinx,y=0,x=![]() ,y=
,y=![]() сызықтармен шектелген аудан неге тең?
сызықтармен шектелген аудан неге тең?
4.y=ex,x=1,x=0,y=0 сызықтармен шектелген аудан неге тең?
5.y=x2-4x+4 жәнеy=x сызықтармен шектелген аудан неге тең?
A.2 B.5 C.12 D.![]() E.
E.![]()
Үйге тапсырма: №15-№20 5 нұсқа 2014 ж тест
Бағалау және қорытындылау:
Туынды деген не?
Алғашқы функцияны қалай табады?
Сабақ: №26,27
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Қарапайым геометриялық фигуралар (планиметрия есептері)
Сабақтың мақсаты:
Білімділік: Планиметрия есептері тақырыбы бойынша оқушылардың білімдерінің деңгейі мен тиянақтылығын тексеру және бағалау.
Тәрбиелік: ұжымдастыққа. бірізділікке. сыйластыққа тәрбиелеу
Дамытушылық: оқушылардың ойлау қабілеті мен дағдыларын дамыту.
Сабақтың типі: білім мен дағдыны жүйелеу
Сабақтың әдісі: жеке, топтық, деңгейлік
Сабақтың түрі: аралас сабақ
Сабақтың көрнекілігі: оқулық,тест тапсырмалары
Сабақтың жүрісі:
І.Ұйымдастыру
II.Планиметрия есептері жайында түсініктеме беру:
-
Көпбұрыш; Тік төртбұрыш Үшбұрыш
-
Параллелограмм Ромб
-
Трапеция Шеңбер ,дөңгелек
III.Есептер шығару:
Дөңгелектің ауданы
-
Дөңгелектің ауданынын формуласын анықта.
А) Sq =ПR2 Б) С=2ПR В)(х-а)²+(у-в)²=R²
-
Дөңгелектің ауданын 2 есе арттыру үшін R-сын неше есе арттыру керек.
А) 1 Б) 3 В) ![]()
-
Дөңгелектің R= 10 см. Ауданын тап.
А) 314 см² Б) 362 см В) 928 см²
-
Егер дөңгелектің диаметрін 2 есе үлкейтсе, онда дөңгелектің ауданын неше есе үлкейеді?
А) 2 есе Б) 3 есе В) 4 есе
-
Егер шеңбердің ұзындығы L, болса дөңгелектің ауданын тап.
А) ![]() Б)
Б) ![]() В) ПR²
В) ПR²
-
Дөңгелектің R=5 см. Ауданын тап.
А) 78,5 Б) 79,9 В) 75
-
Дөңгелектің ауданын 3 есе арттыру үшін R-сын неше есе арттыру керек.
А) ![]() Б) 6 В) 9
Б) 6 В) 9
-
Егер дөңгелектің диаметрін 6 есе үлкейтсе, онда дөңгелектің ауданы неше есе үлкейеді?
А) 12 Б) 36 В) 14
9. Дөңгелектің R=20 см. Ауданын тап.
А) 1256 Б) 120 В) 200
-
Дөңгелектің ауданын 7 есе арттыру үшін. R-сын неше есе арттыру керек.
А) 7 Б) 14 В) 49
Шеңбердің ұзындығы.
-
Шеңбердің ұзындығының теңдеуін тап.
А) С=2ПR Б) Sq=ПR² В) С=2П
-
R=7 см болатын шеңбердің ұзындығын тап.
А) 14П см Б) 49П В) 9П
-
R=2 см болатын шеңбердің ұзындығын тап.
А) 4П см Б) 5П см В) 6П см
-
Шеңбердің ұзындығы 4П болатын, R=?
А) R=2 Б) R=4 В) R=6
-
Шеңбердің ұзындығы 6П болатын, R=?
А) R=3 Б) R=8 В) R=4
-
R=5 см болатын шеңбердің ұзындығын тап.
А) 10П Б) 25П В) 15П
-
R=8 см болатын шеңбердің ұзындығын тап.
А) 16П Б) 9П В) 8П
-
Шеңбердің ұзындығы 8П болатын, R=?
А) R=4 Б) R=8 В) R=16
IV.Үйге тапсырма:
№7-№10 .Өтілген тақырыпты оқу
V.Бағалау және қорытындылау
Сабақ: №28,29
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Векторлар
Сабақтың мақсаты:
а)Вектор,кеңістіктегі векторлардың координаталары ұғымдарымен таныстыру, векторларға амалдар қолдануға есептер шығару
ә)Оқушыларға сызба салуда ұқыптылыққа, сауаттылыққа, яғни эстетикалық тәрбие беру;
б)Оқушылардың абстрактылы ойлау қабілетін дамыту;
Сабақтың типі: Жаңа сабақ
Сабақтың түрі: Жаңа білім игеру сабағы
Сабақтың көрнекілігі: оқулық
Пән аралық байланыс: Сызу
Сабақтың барысы:
1.Ұйымдастыру
А)оқушының сабаққа қатысыБ)психологиялық дайындығы, зейінін шоғырландыру
2.Жаңа тақырыпты баяндау:
-
В
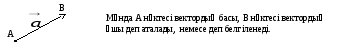 ектордың
негізгі элементтері, белгіленуі.
ектордың
негізгі элементтері, белгіленуі.
-
Вектордың координаттары.
![]() болса,
онда
болса,
онда ![]() векторының координаттары мына формуламен аныкталады:
векторының координаттары мына формуламен аныкталады: ![]()
-
Вектордың абсолют шамасы (ұзындығы):
![]() болса,
онда
болса,
онда ![]()
-
Векторларды қосу:
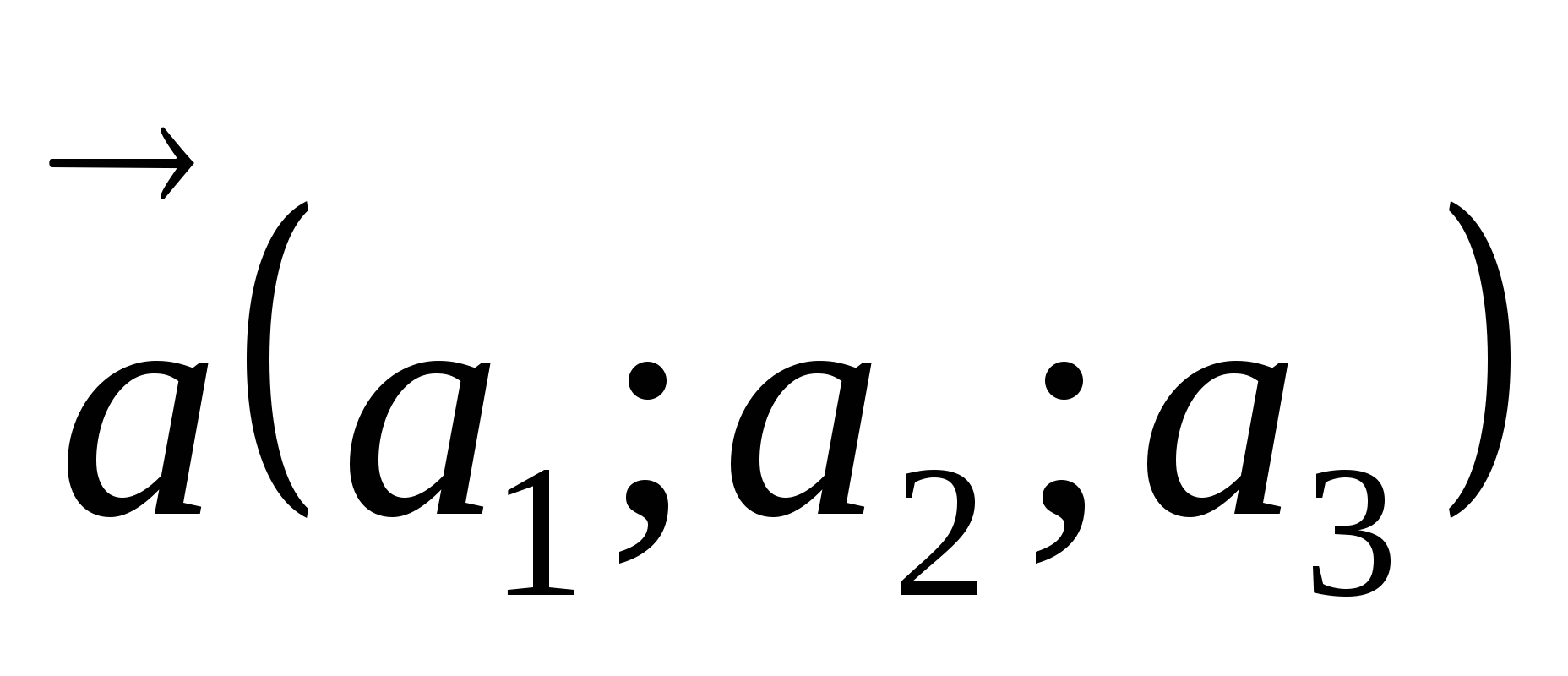 ,
, 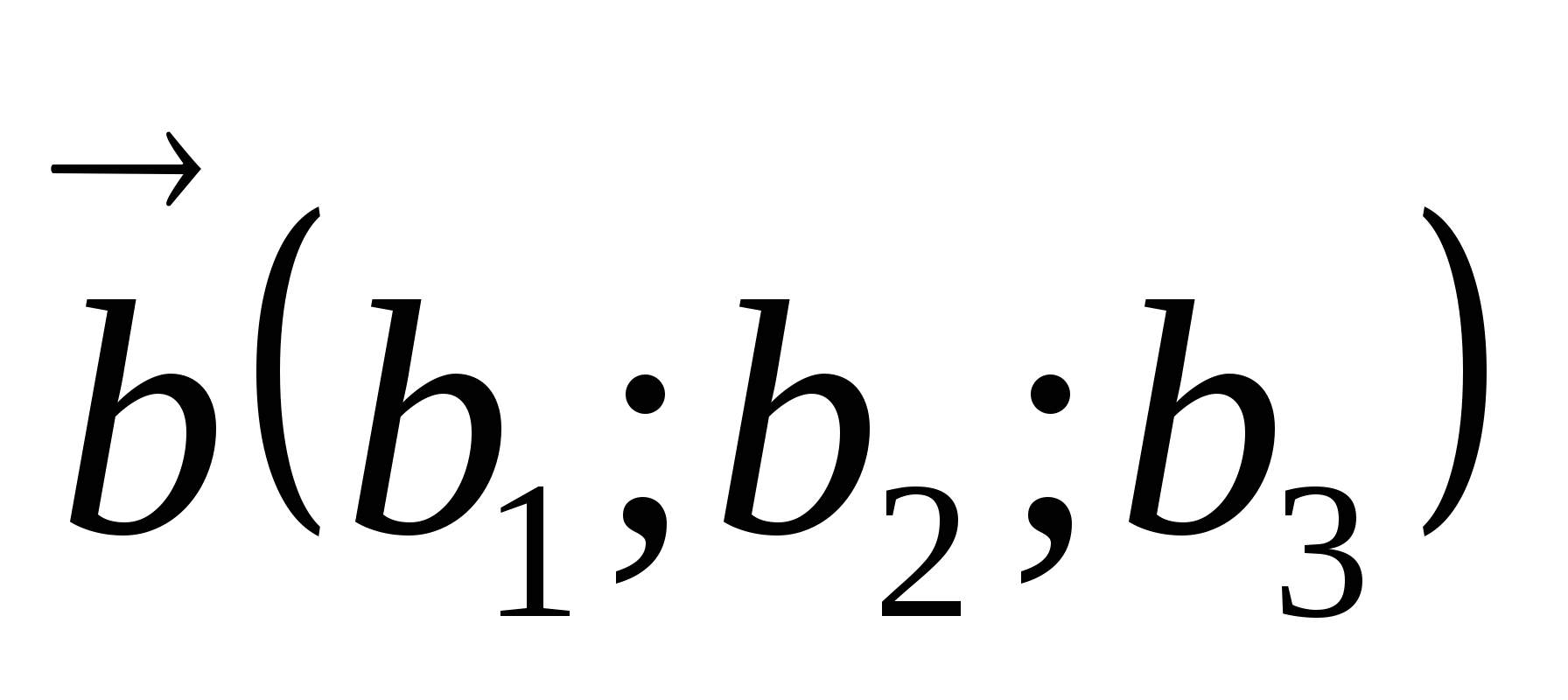 векторларының қосындысы вектор болады және оның координатасы
былай анықталады:
векторларының қосындысы вектор болады және оның координатасы
былай анықталады: 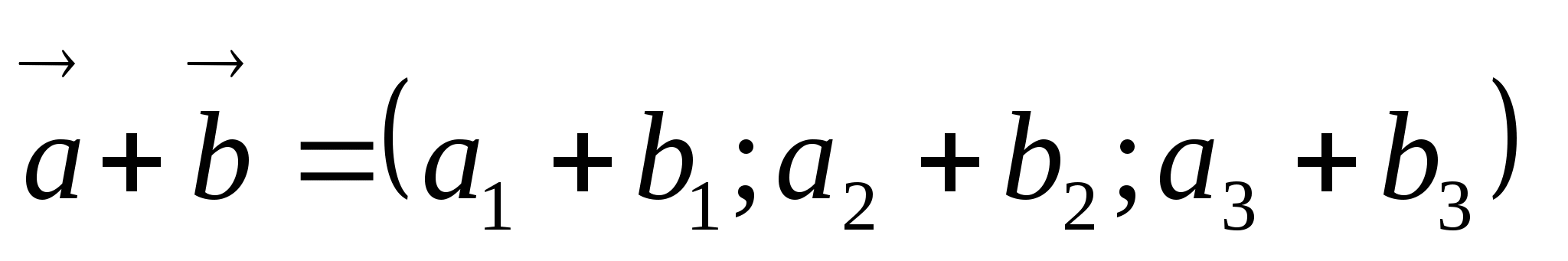
-
Векторды санға көбейту:
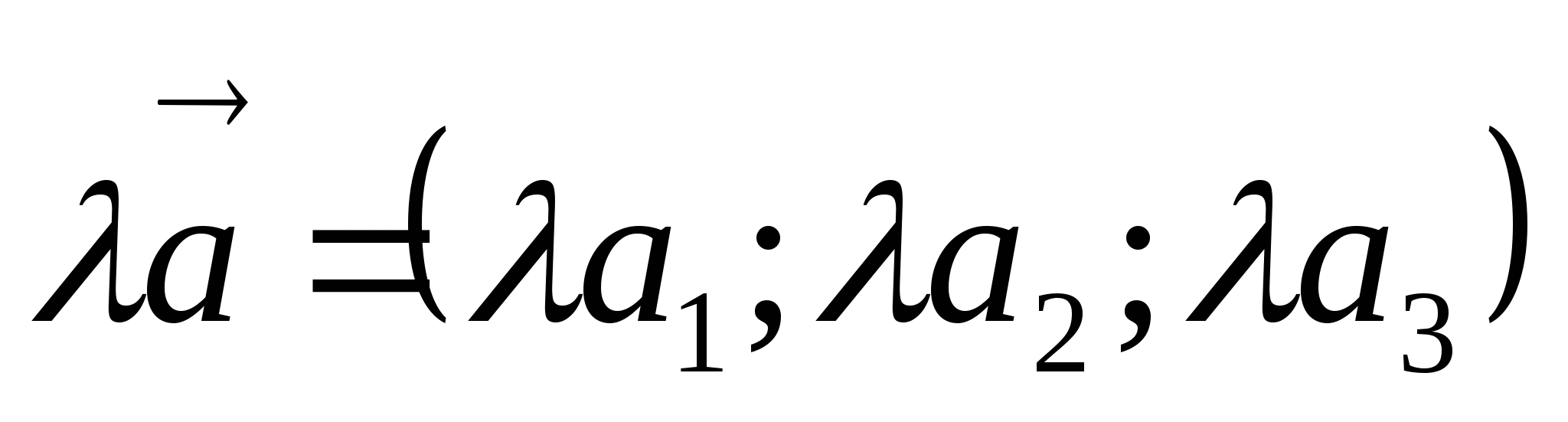
-
Коллинеар векторлардың координаталары үшін келесі теңдік орындалады:
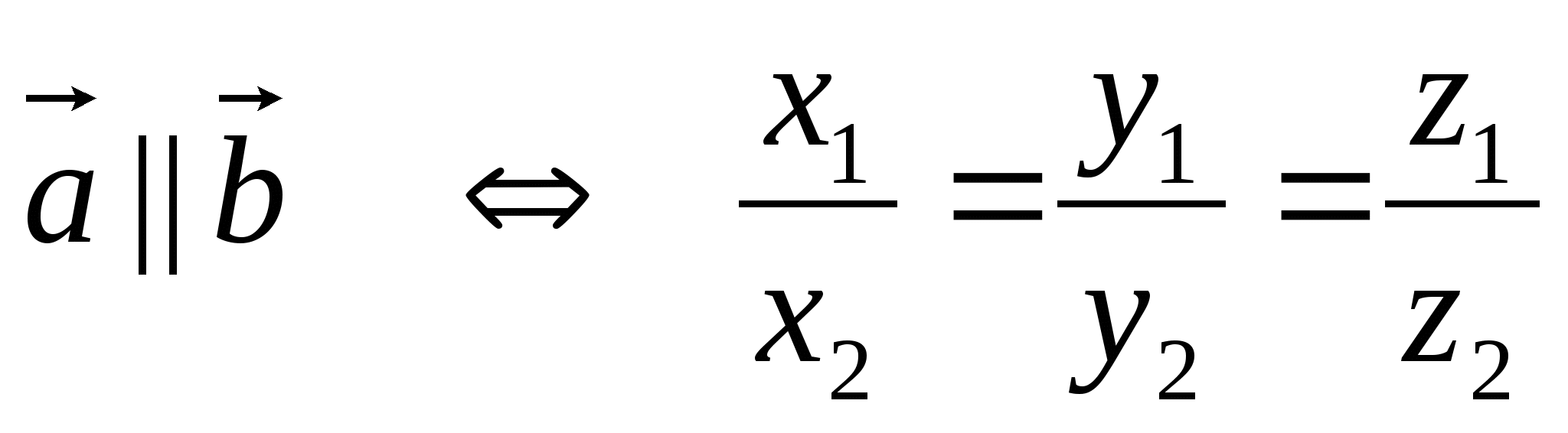 , мұнда векторлардың координаталарының ешқайсысы нөлге тең
болмау керек. Егер екі вектордың біреуінің қандай да бір
координатасы нөлге тең болған жағдайда екінші вектордың да оған
сәйкес координатасы нөлге тең болуы керек.
, мұнда векторлардың координаталарының ешқайсысы нөлге тең
болмау керек. Егер екі вектордың біреуінің қандай да бір
координатасы нөлге тең болған жағдайда екінші вектордың да оған
сәйкес координатасы нөлге тең болуы керек.
-
Векторлардың скаляр көбейтіндісі:
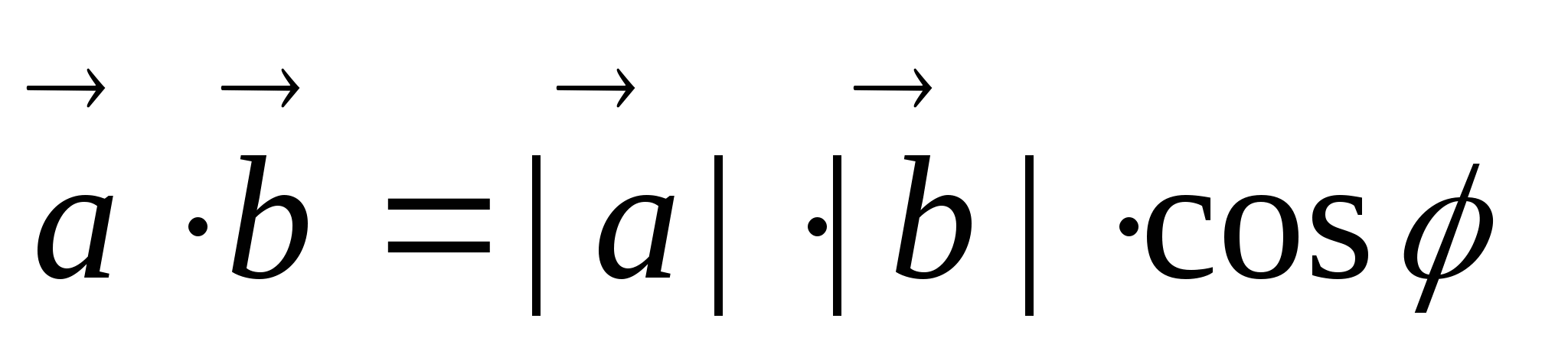 .
.
Егер ![]() ,
, ![]() болса, онда
болса, онда ![]() болады.
болады.
Векторлар арасындағы бұрыш
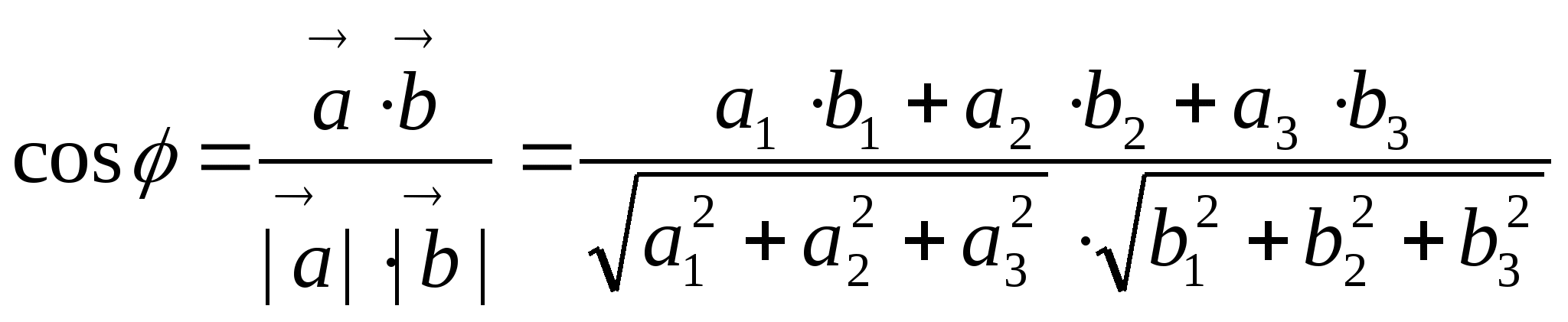
![]() - сүйір
- сүйір ![]()
![]() .
.
![]() -
доғал
-
доғал ![]()
![]() .
.
![]()
![]()
![]() .
.
.
![]()
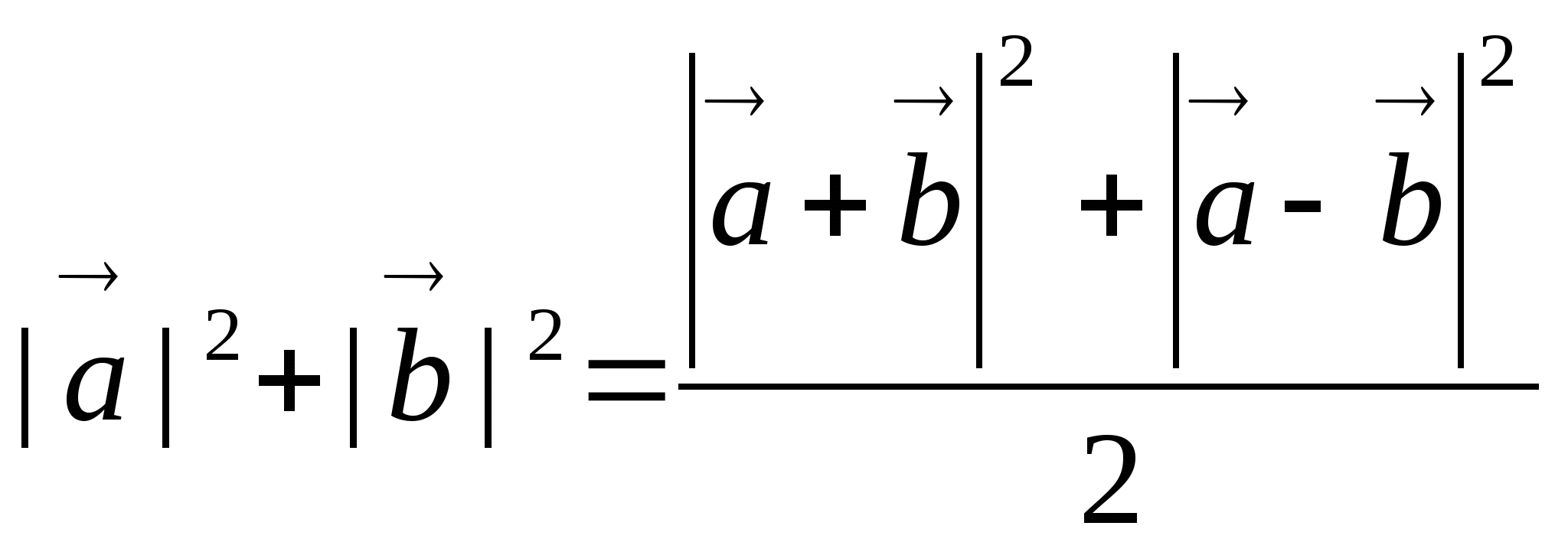 .
.
-
Параллелограмның қасиеті бойынша:

-
Ұзындығы бірге тең векторды бірлік вектор немесе орт дейміз. Кез келген векторды бірлік векторлар арқыл
-
ы жіктеуге болады.
![]()
![]()
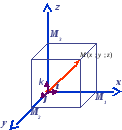
![]()
![]()
![]()
3.Есептер шығару:
1 есеп. Кеңістікте М(1; 3; 0) және N(-2; 5; 4) нүктелері берілген. МN векторын тап.
2 есеп. m (3; 2; 1) және n (-2; -1; 6) векторларының ұзындықтарын есептеңіз.
3 есеп. В (-4; 0; 2), С (-7; -4; -3) нүктелерінің ара қашықтығын табыңыз
4 есеп. а (2; 4; 0) және b. (5; -1; 2) берілген. a + b табыңыз.
5 есеп. М (6; -6; -7) нүктесі берілген. Радиус вектор ұзындығын анықтаңыз.
6 есеп. М (-3; 4; 0) және N (-5; 2; 6) нүктелерінің ара қашықтығын табыңыз
4.Үйге тапсырма: №8-№10 есеп . Векторларға амалдар қолдану тақырыбын оқу
5.Қорытындылау
Сабақ: №30,31
Бекітемін:
Сынып: Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Көпжақтар
Сабақтың мақсаты:
1. Білімділігі: Көпжақтардың периметрін,ауданын табуға есептер шығару
2. Дамытушылық: Логикалық ойлау қабілеті мен есептеу дағдыларын жетілдіру, өз бетінше еңбектену, белсенділіктерін арттыру, пәнге қызуғушылығын ояту, оқушылардыңқұзыреттерін қалыптастыру.
3.Тәрбиелік: Оқушылардыңөз ойын толық, дұрыс жеткізе білуге, тапқырлыққа, жылдамдылыққа, ептілікке, достыққарым-қатынасқа тәрбиелеу.
Сабақтың типі: білім мен дағдыны жүйелеу Сабақтың әдісі: жеке, топтық, деңгейлік
Сабақтың түрі: аралас сабақ Сабақтың көрнекілігі: оқулық
Сабақтың жүрісі:
1.Ұйымдастыру
2.Есептер шығару:
-
Параллелограммның қабырғалады 12 см және 15 см. Үлкен қабырғасына түсірілген биіктігі 8 см болса, кіші қабырғасына түсірілген биіктігін табыңыз.
А)10 см; В) 5см; С) 4см; Д)7см; Е)6см.
-
Ромбының қабырғасы 17 см және бір диагоналі 16 см. Келесі диагоналін табыңыз:
А)20см; В)30 см; С)40см; Д) 55см; Е) 23см.
-
Параллелограммның бір бұрышы 400. бұған тең емес келесі бұрышын табыңыз.
А)60![]() В)45
В)45![]() С)1400 ; Д) 120
С)1400 ; Д) 120![]() ;
Е) 65
;
Е) 65![]()
-
Параллелограммның қабырғалары 8 см және 10 см, сүйір бұрышы 600. Параллелограммның ауданын табыңыз:
А)120см![]() В) 75см
В) 75см![]() С)40
С)40![]() Д)
Д)![]() ;
Е)168см
;
Е)168см![]()
-
Параллелограммның диагоналі оның қабырғаларымен 250 және 350 бұрыш жасайды. Параллелограммның бұрыштарын табыңыз.
А) (52![]() В) (60
В) (60![]() С) (30
С) (30![]() ;
Д)(600; 1200); Е) (45
;
Д)(600; 1200); Е) (45![]()
-
Тік төртбұрыштың диагоналі оның бұрышын біреуі 200 болатындай 2 бөлікке
бөледі. Бұрыштың екінші бөлігін табыңыз.
А)60![]() В)45
В)45![]() С)1400 ; Д) 120
С)1400 ; Д) 120![]() ;
Е)800
;
Е)800
-
NPKM тік төртбұрышының NK диагоналі
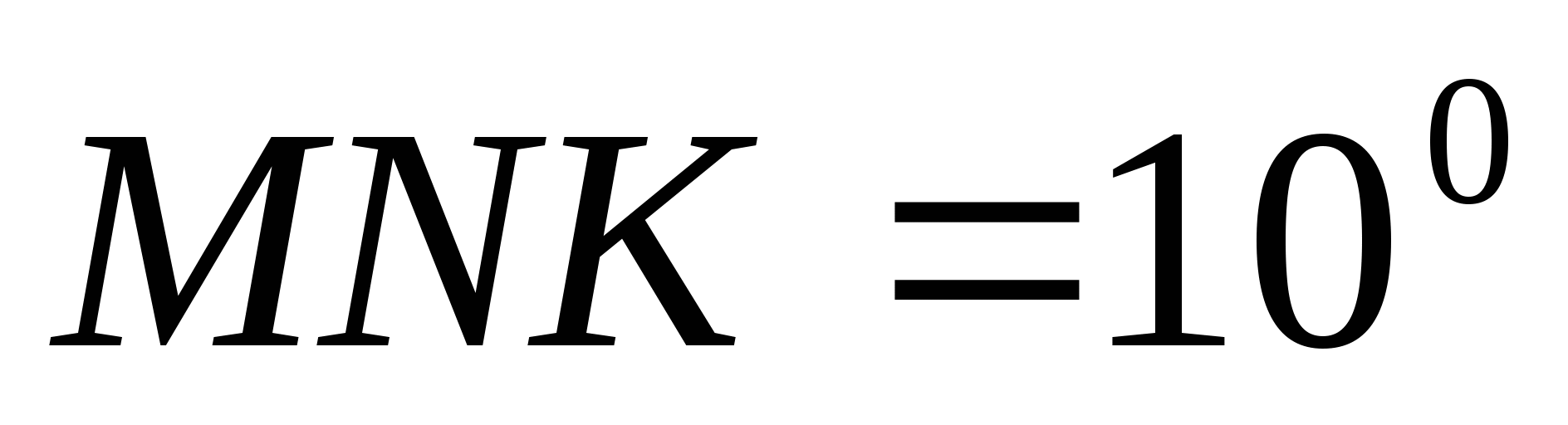 болатындай бұрыш қояды. МОК бұрышын табыңыз, егер
О-диагональдарының қиылысу нүктесі болса.
болатындай бұрыш қояды. МОК бұрышын табыңыз, егер
О-диагональдарының қиылысу нүктесі болса.
А)60![]() В)45
В)45![]() С)1400 ; Д) 120
С)1400 ; Д) 120![]() ;
Е) 200
;
Е) 200
-
Диагональдардың қиылысу нүктесінен қабырғаларына жүргізілген перпендикулярларының ұзындығы 2 дм және 4 дм екендігін ескеріп, тік төртбұрыштың периметрін табыңыз.
А)24 дм; В)30 дм; С)40дм; Д) 55дм; Е) 23дм.
-
АВСД тік төртбұрышының қабырғаларын табыңыз, егер А төбесінен ВС қабырғасына жүргізілген АМ кесіндісі
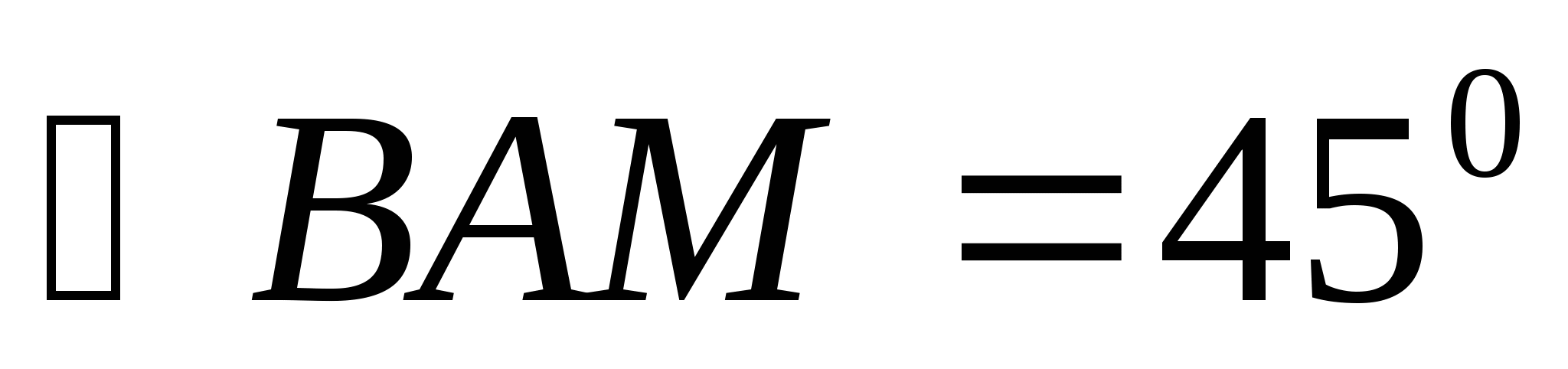 -қа тең, ал МС-МВ=3 см. Тік төртбұрыштың периметрі 24 см.
-қа тең, ал МС-МВ=3 см. Тік төртбұрыштың периметрі 24 см.
А)3 см және 9 см; В) 5см және 7см; С) 4см және 6см; Д) 7см және 8см; Е) 11см және 9см.
-
Тік төртбұрыш диагональдарының қиылысу нүктесі кіші қабырғасынан үлкен қабырғаға қарағанда 4 см алысырақ.
А) 13см; 10см; В)10 см; 18 см; С) 4см; 6см; Д) 7см;8см; Е) 11см;9см
3.Үйге тапсырма:№9,№10
4.Қорытындылау:Қарапайым геометриялық фигуралар деген не?
Сабақ: №32,33
Сынып: Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Айналу денелері
Сабақтың мақсаты:
Білімділік: Айналу денелері тақырыбы бойынша оқушылардың білімдерінің деңгейі мен тиянақтылығын тексеру және бағалау.
Тәрбиелік: ұжымдастыққа. бірізділікке. сыйластыққа тәрбиелеу
Дамытушылық: оқушылардың ойлау қабілеті мен дағдыларын дамыту.
Сабақтың типі: білім мен дағдыны жүйелеу
Сабақтың әдісі: жеке, топтық, деңгейлік
Сабақтың түрі: аралас сабақ
Сабақтың көрнекілігі: оқулық,тест тапсырмалары
Сабақтың жүрісі:
І.Ұйымдастыру бөлімі
II.Есептер шығару:
№1 есеп
Конустың жасаушысы 12 дм және табан жазықтығына 300 бұрышпен көлбеген. Конустың биіктігін табыңыз.
Sin300=H/L, 1/2= H/12 , H=6 , Жауабы: 6 (дм)
№2 есеп
Конустың биіктігі 20 см, табанының радиусы 15 см. Бүйір бетінің ауданын табыңыз.
Sк.б.б. =ПRL
L2= H2 + R2 = 400 + 225 = 625, L= 25см
Sк.б.б. =П* 15* 25 = 375 П см2, Жауабы: 375 П см2
№3 есеп
Конустың жасаушысы 5 см, табанының радиусы 4 см. Толық бетінің ауданын табыңыз.
Sк.тол.беті =ПRL + ПR2
Sк.б.б. =П * 4 *5 = 20 П,
Sтаб =П * 42= 16П
Sк.тол.беті = 20П + 16П = 36П Жауабы: 36П (см2)
№4 есеп
D=12 см Шешуі: Sт.б= 2ПRH + 2П R2
H= 3,5 см R = D/2 = 12/2 = 6см
т/к: Sт.б=? Sц.бб= 2ПRH=2П*6*3,5=42П (см2)
Sт=2П R2= 2П*62= 72П (см2)
Sт.б= 2ПRH + 2П R2= 42П + 72П = 114П см2
Жауабы: 114П см2
Үйге тапсырма: Бос ұяшықты толтырыңыздар
-
Сабақты қорытындылау: қайталау
Сабақ: № 34
Сынып:
Күні:
Пән: Таңдау курсы
Сабақтың тақырыбы: Тест тапсырмалары
Сабақтың мақсаты:
1. Білімділік: Оқушылардың өтілген тақырыптар бойынша алған білімдерін тұжырымдай отырып, берілген тапсырмаларда формулаларды тиімді қолдана білу дағдысын қалыптастыру;
2. Дамытушылық: Оқушыларды терең ойлауға және алған білімдерін тапсырмаларды орындау барысында қолдана білу әрекетін және ой-өрісін дамыту;
3. Тәрбиелік: Оқушыларды өздігінен шешім қабылдай отырып, жұмыс істеуге және тапсырманы ұқыпты орындауға, жазуға баулу.
Сабақтың барысы:
Ұйымдастыру кезеңі: оқушылармен сәлемдесу, сабаққа дайындығын, қатысуын тексеру.
Тест тапсырмаларын орындау:
1. Квадраттың қабырғалары 25%-ке ұзартылған. Квадраттың ауданы қанша процентке көбейеді?
A) 52,65%. B) 50%. C) 30%. D) 56,25%. E) 25%.
2. Теңдеуді шешіңіз: 5 - 3(x - 2(x - 2(x - 2))) = 2.
A) 3. B) 7. C) -4. D) 2,2. E) 11.
3. Бөлшектің бөліміндегі иррационалдықтан құтылыңыз:
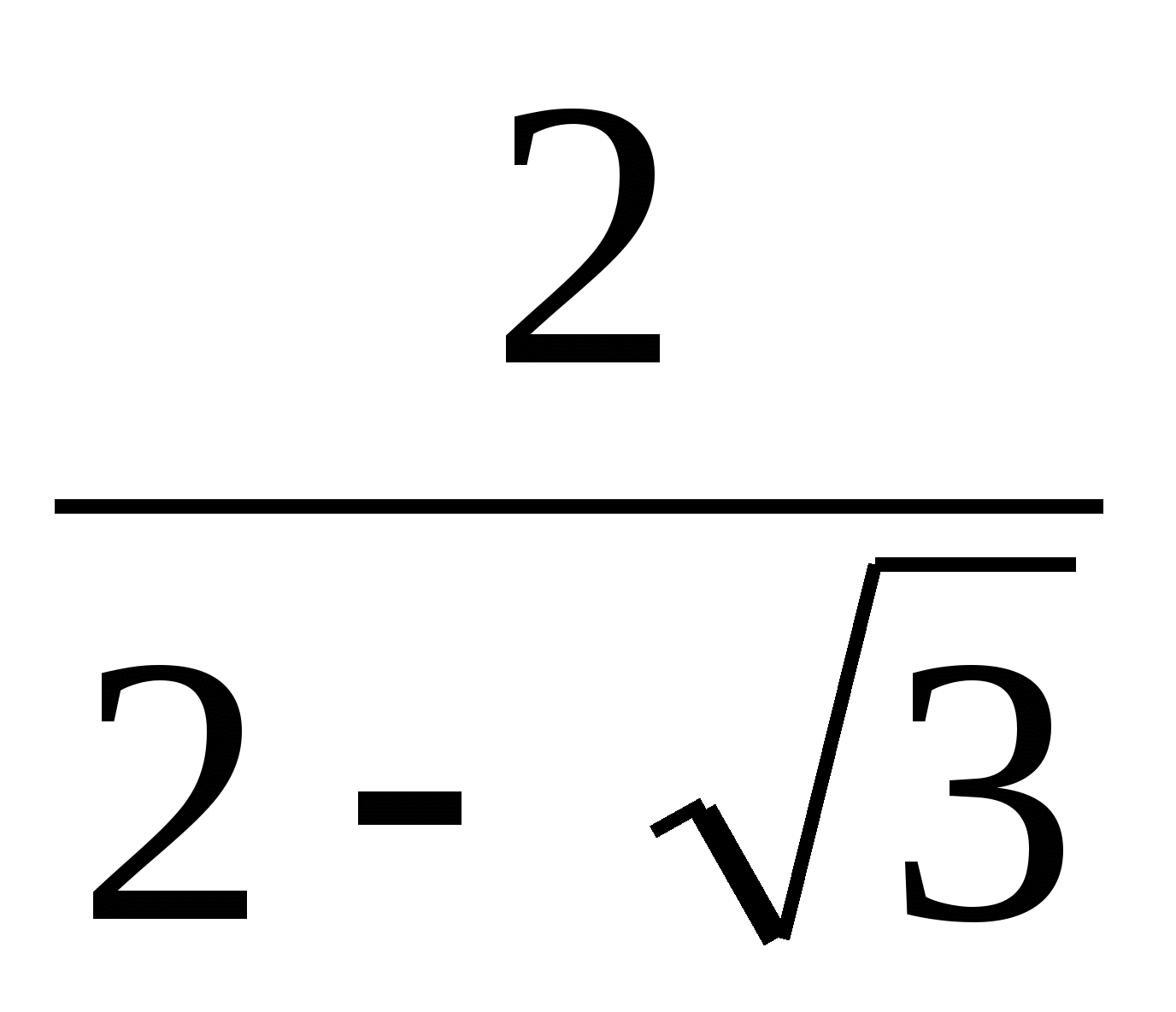 .
.
A)
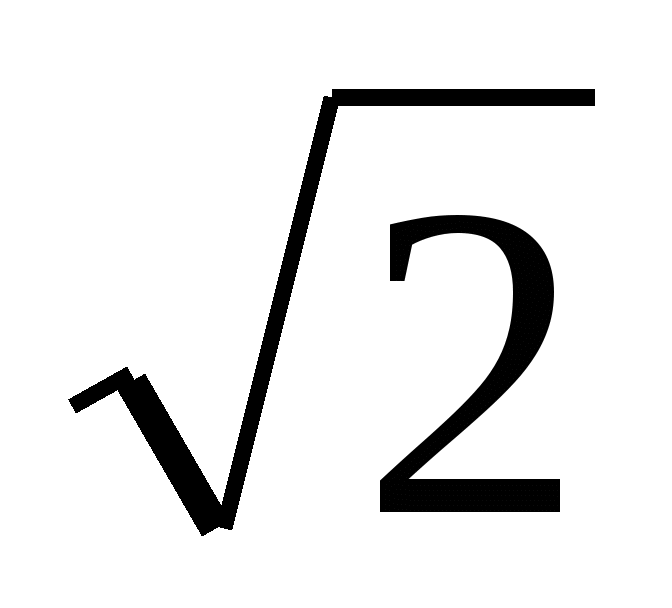 - 3. B) 2 -
- 3. B) 2 - 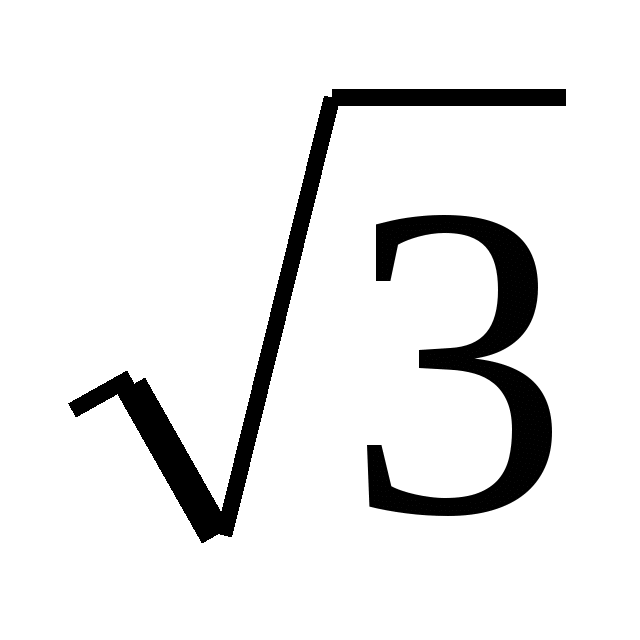 . C)
. C) 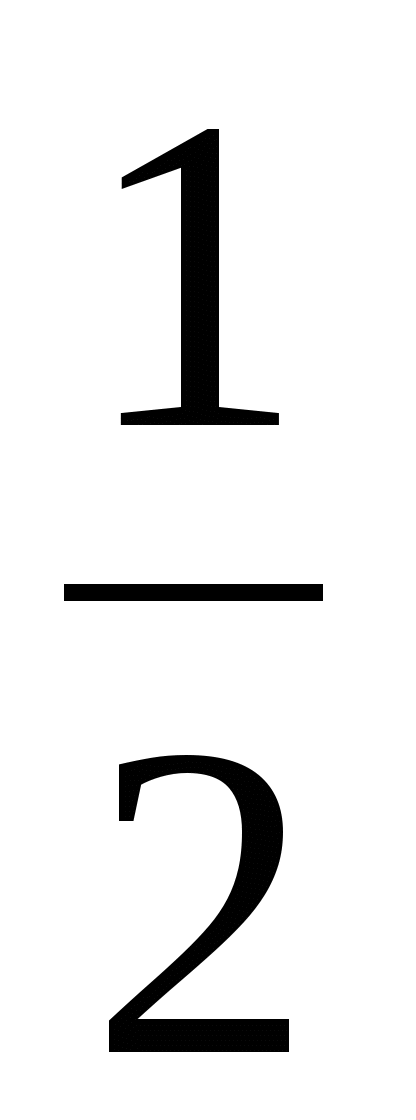 (2 +
(2 + 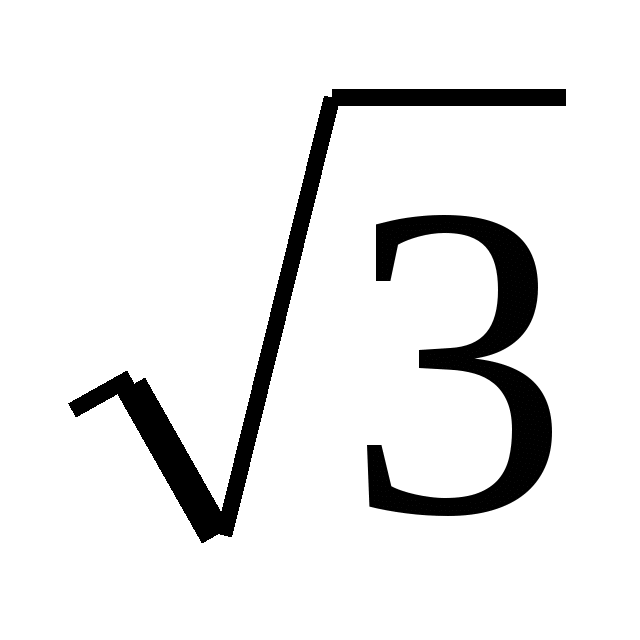 ). D) 2(2 -
). D) 2(2 - 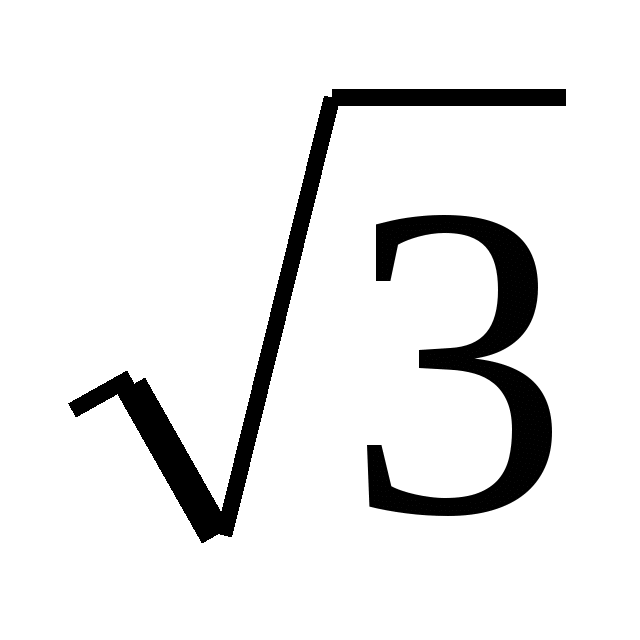 ). E) 2(2 +
). E) 2(2 + 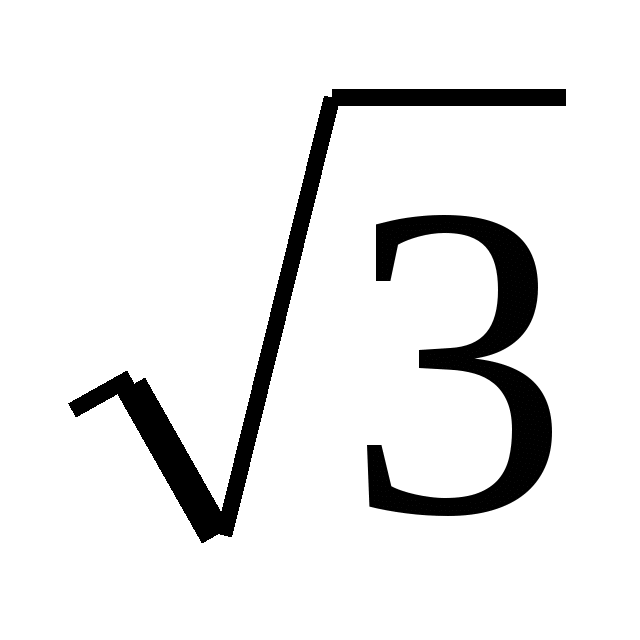 ).
).
4. Теңсіздіктер жүйесін шешіңіз:
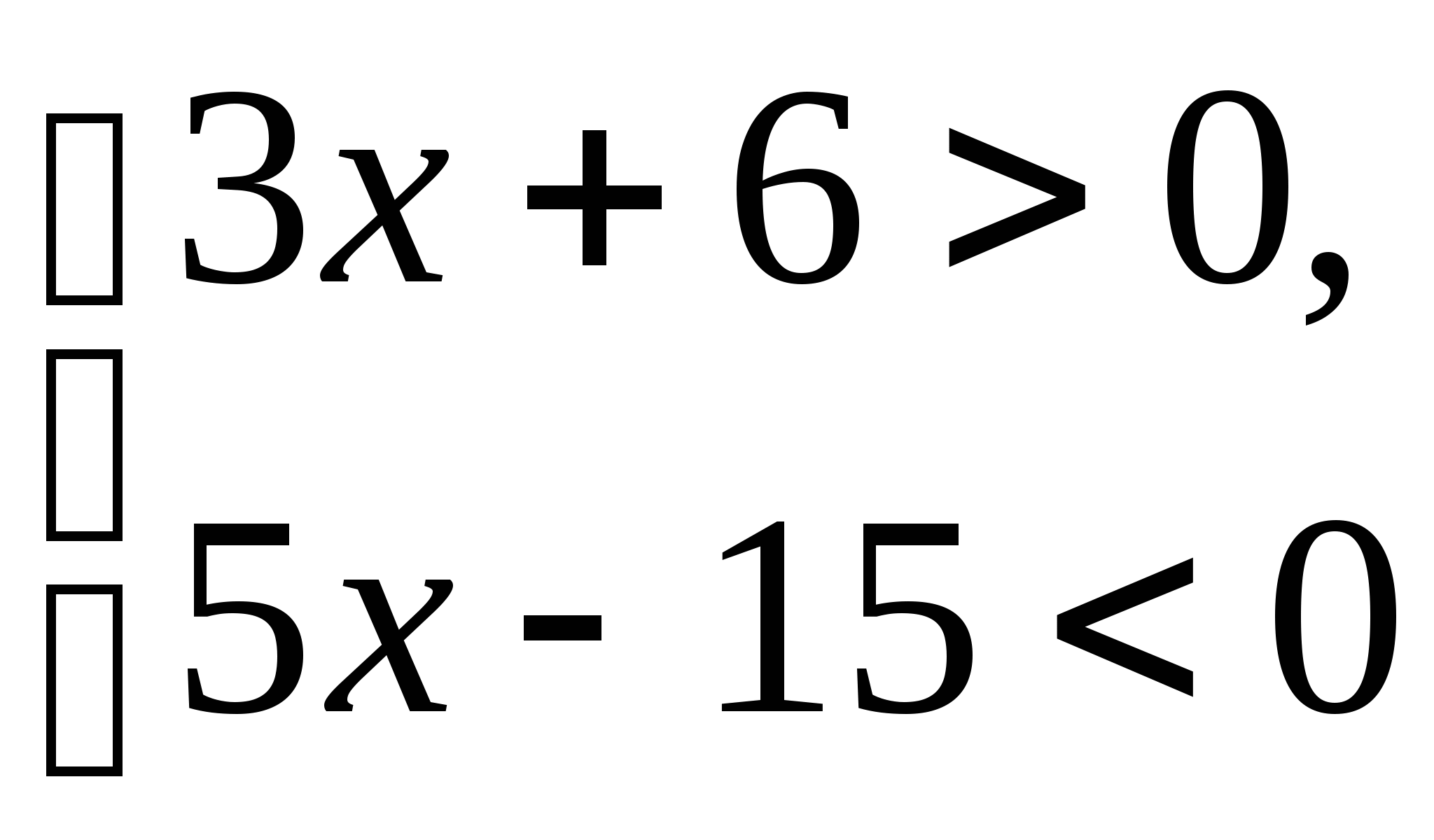
A) (-2; 3). B) [-2; +¥). C) (-¥; 3]. D) (-¥; -2). E) [-2; 3].
5. у-ті х арқылы өрнектеңіз: 2х + 5у - 16 = 0.
A) у = 2,5х - 8. B) у = -0,4х + 3,2. C) у = -2,5х + 8.
D) у = 2,75х - 8. E) у = 2,5х + 8.
6. Жазықтықта тік бұрышты үшбұрыш берілген, гипотенузасы 12 см. Кеңістікте берілген бір нүктеден үшбұрыш төбелеріне дейінгі қашықтық 10 см-ден. Үшбұрыш жазықтығынан кеңістіктегі нүктеге дейінгі қашықтықты табыңыз.
A) 4 см. B) 7 см. C) 8 см. D) 6 см. E) 5 см.
7. Квадраттың диагоналі 4см. Бұл квадраттың қабырғасы басқа квадраттың диагоналі болып табылады. Екінші квадраттың қабырғасын табыңыз:
A) 9см B) 20см C) 4см D) 2см E) 8см
8. Есептеңіз:
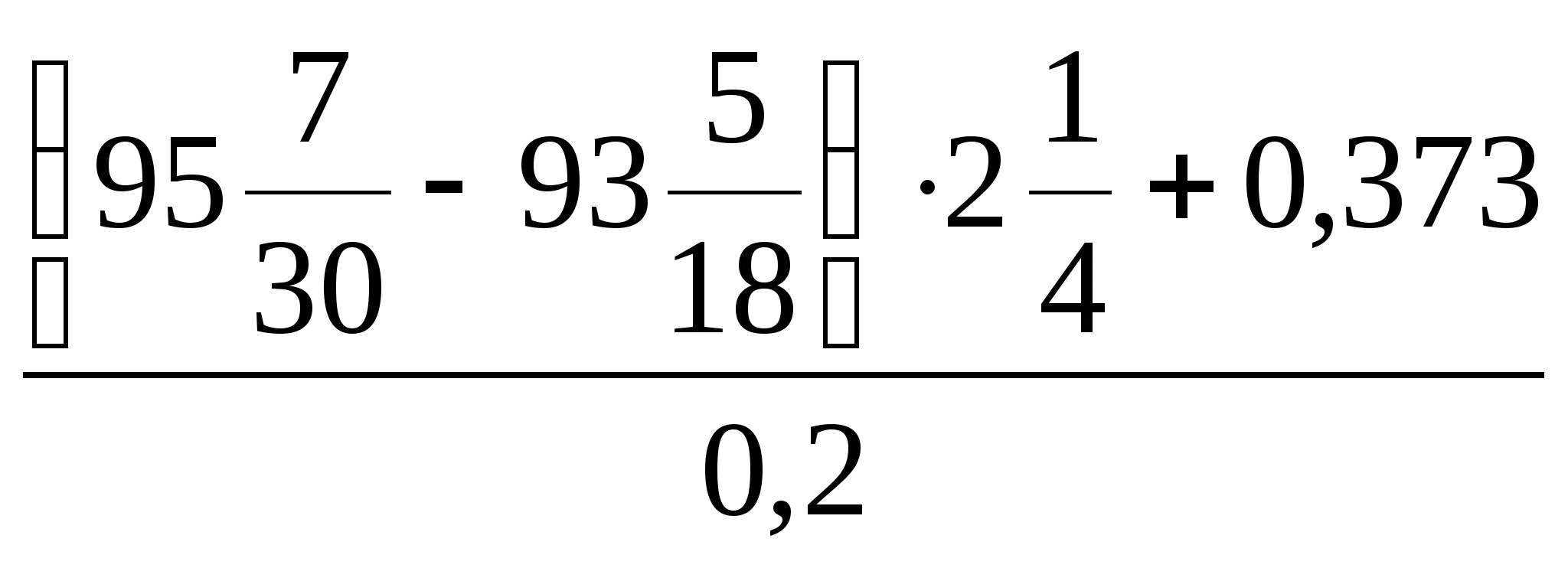
A) 23,456. B) 23,683. C) 23,865. D) 20,850. E) 14.
9. f(х) = х
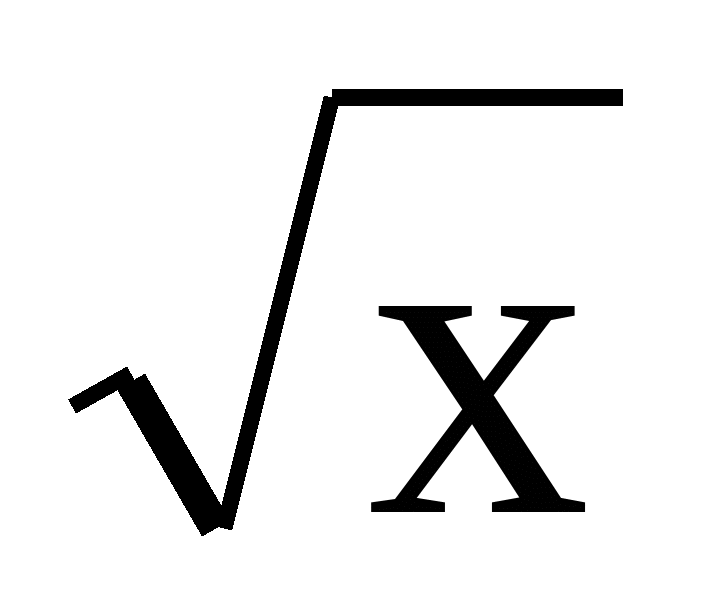 функциясының туындысын табыңыз.
функциясының туындысын табыңыз.
A)
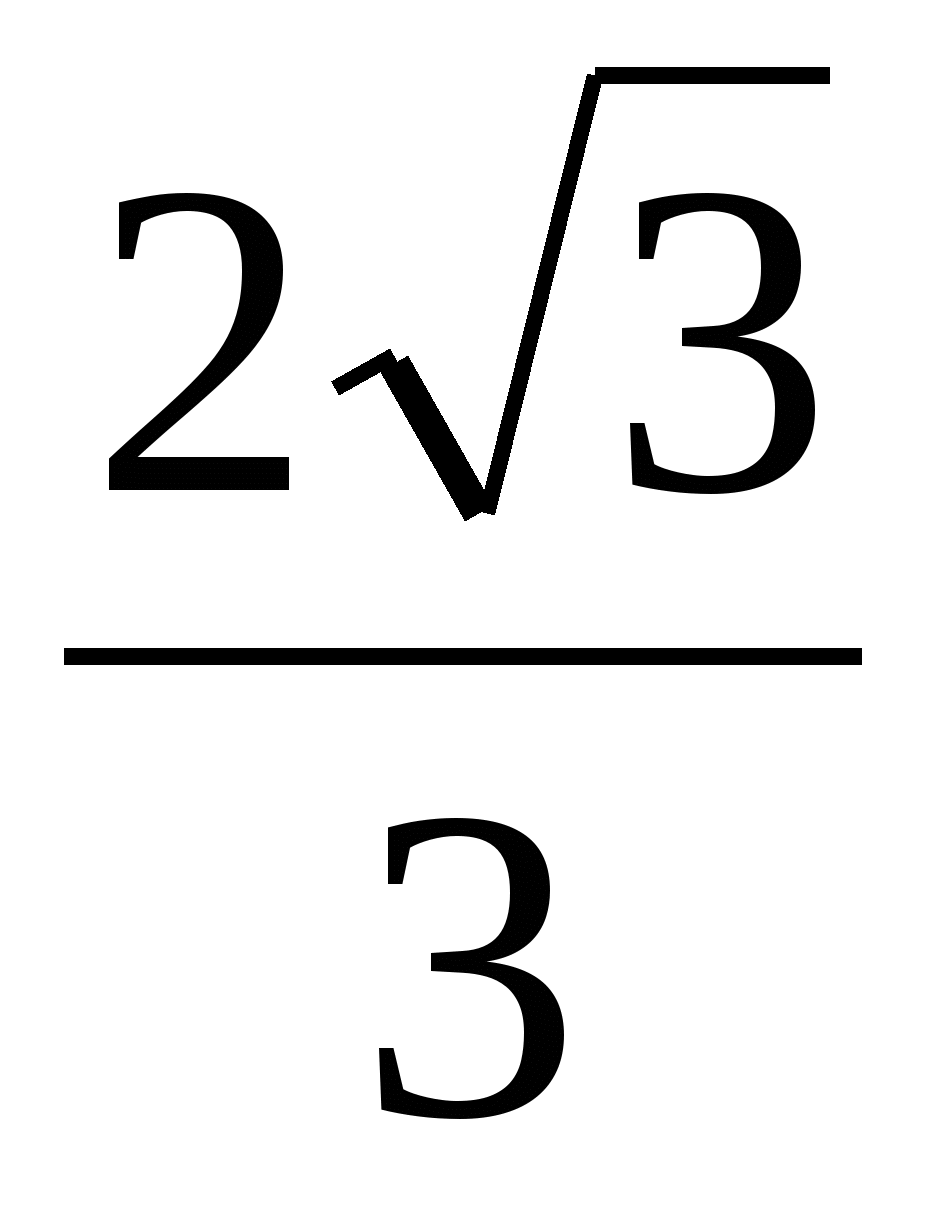 . B)
. B) 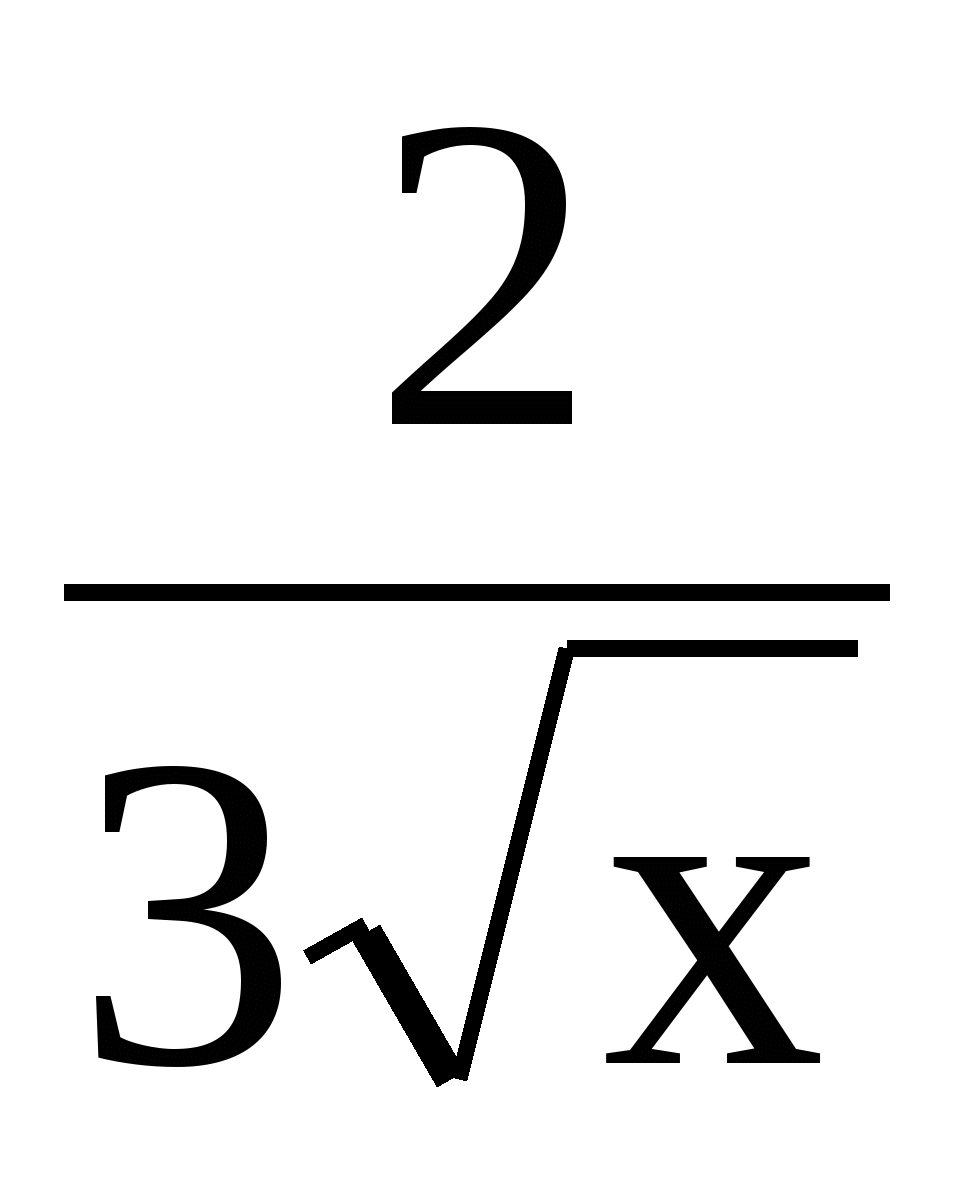 . C)
. C) 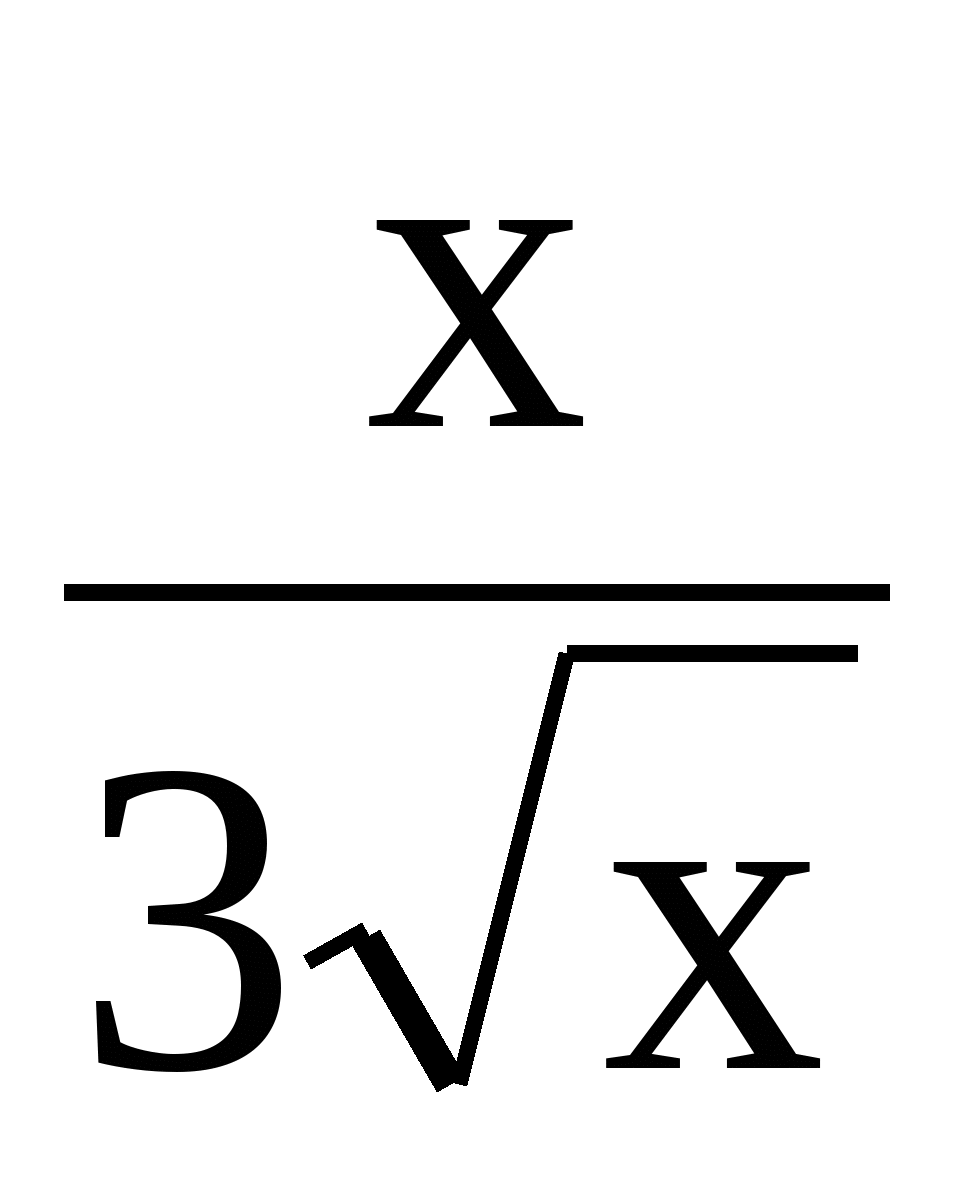 . D)
. D) 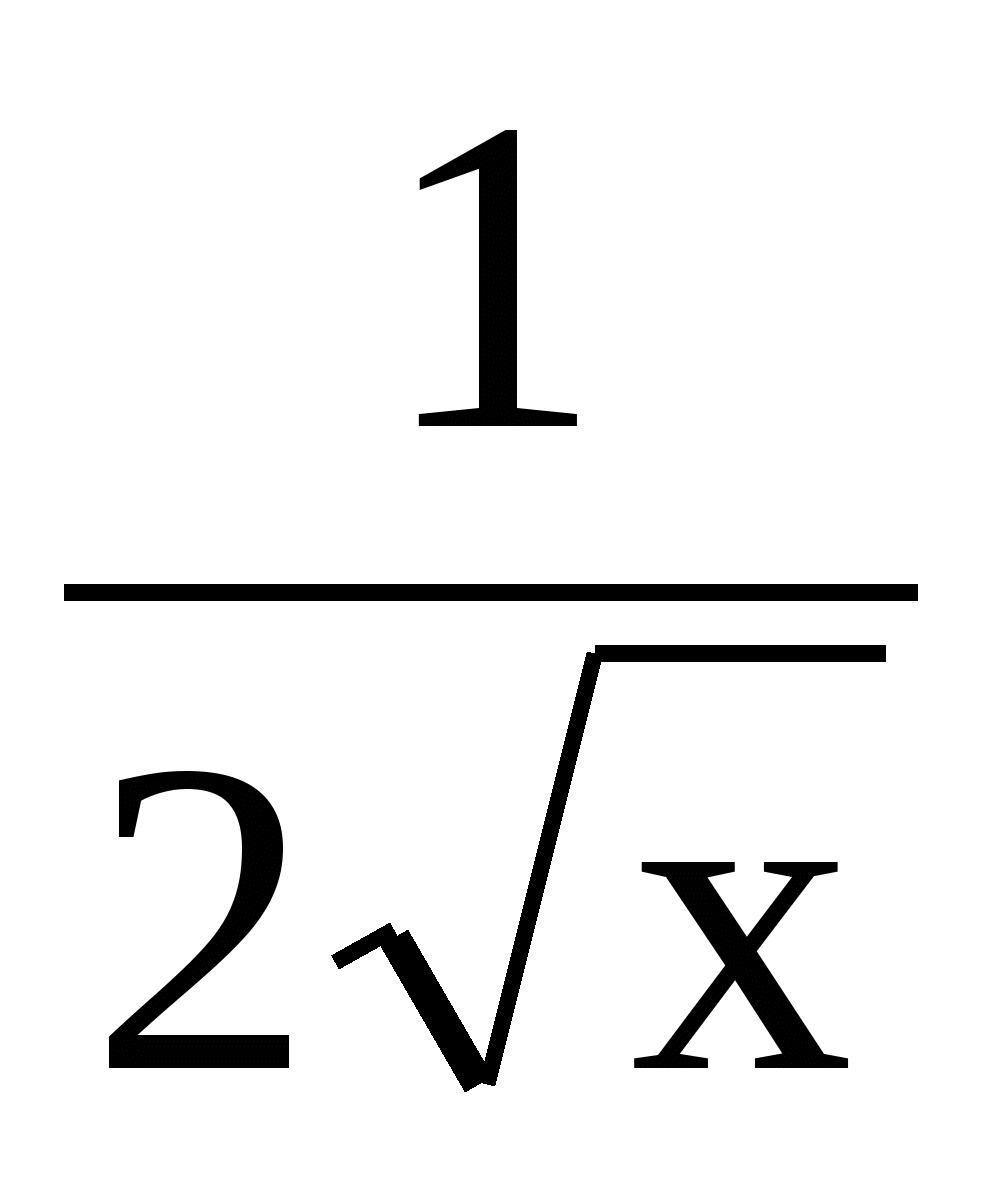 . E) 1,5
. E) 1,5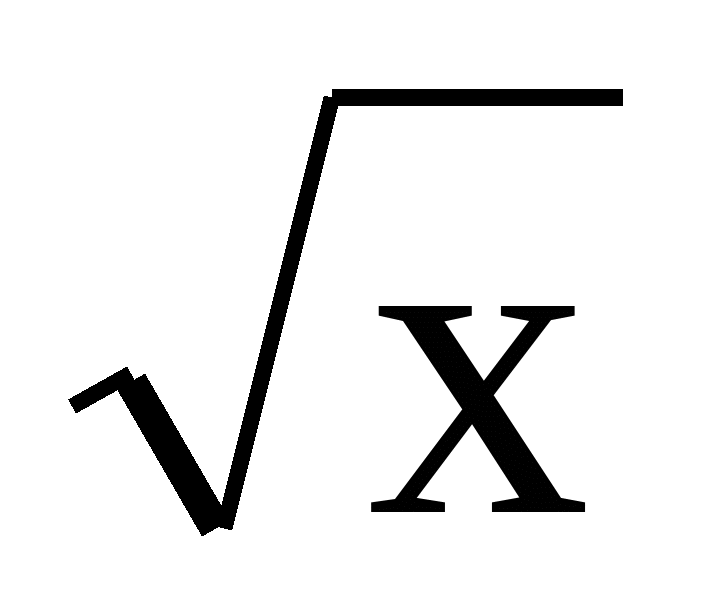 .
.
10. Теңдеуді шешіңіз: 0,35:0,6=x:0,18.
A) 0,105. B) 105. C) 10,5. D) 1,05. E) 0,15.
11. Сөйлемді толықтырыңыз:
"Сызықтық функцияның графигі ... болады".
A) кесінді B) сәуле C) гипербола D) түзу сызық E) парабола
12. ABC үшбұрышының A және B төбелеріндегі сыртқы бұрыштардың қосындысы (әрбір төбеден бір-бірден алынған) қосындысы 2400-қа тең. Үшбұрыштың C бұрышын табыңыз.
A) 900 B) 600 C) 450 D) 300 E) 1800
13. Параллелограмның бір бұрышы екіншісінен 50°-қа үлкен болса, оның бұрыштары неге тең?
A) 95°; 85°. B) 145°; 35°. C) 85°; 35°. D) 60°; 120°. E) 65°; 115°.
14. Тік төртбұрыштың периметрі 80см, ал қабырғаларының қатынасы 2:3 қатынасындай. Тік төртбұрыштың ауданын табыңдар.
A) 325 см2. B) 684см2. C) 384см2. D) 144см2. E) 524см2 .
15. Теңдеуді шешіңіз: (7
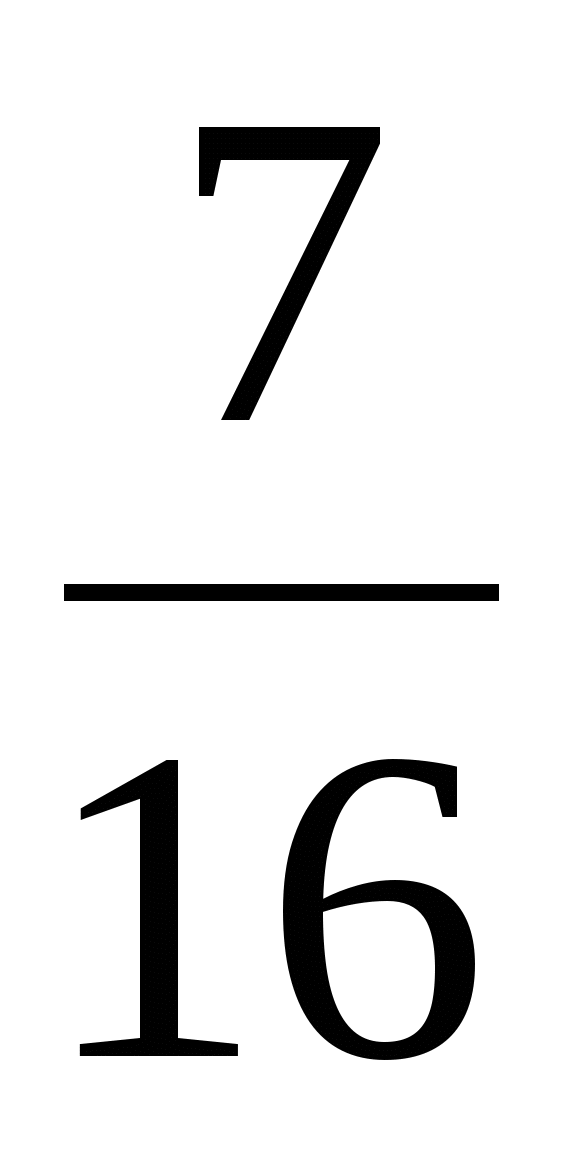 - 6
- 6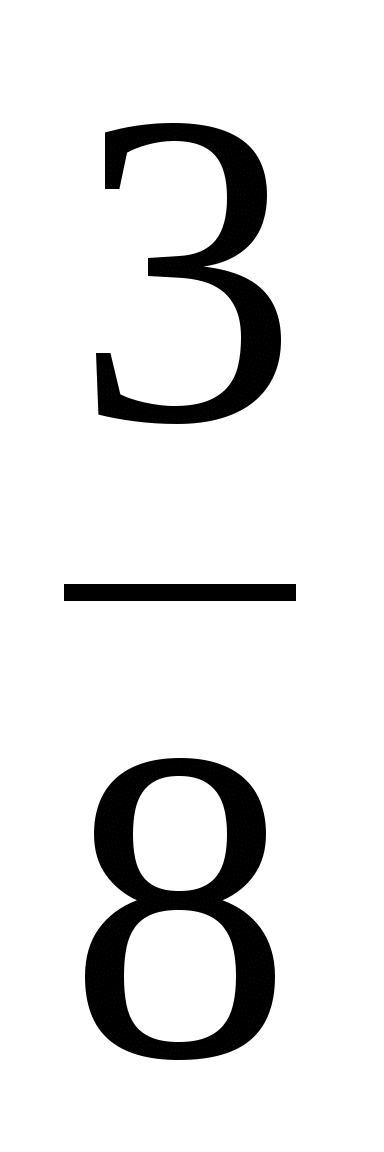 )
y=8
)
y=8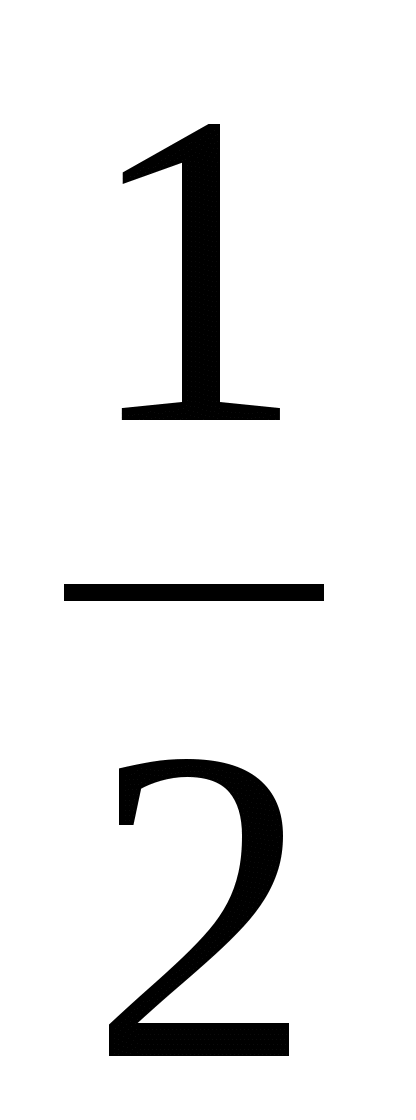
A) 8 B) 5
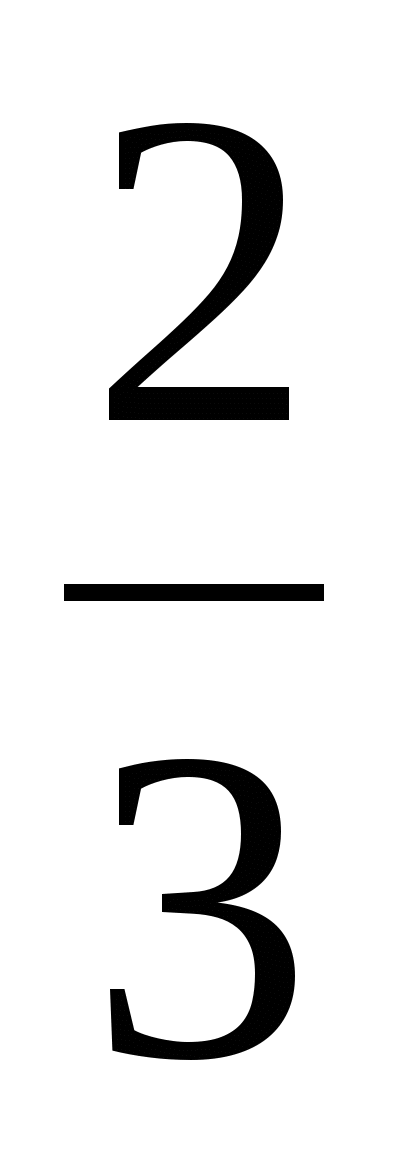 C) 9
C) 9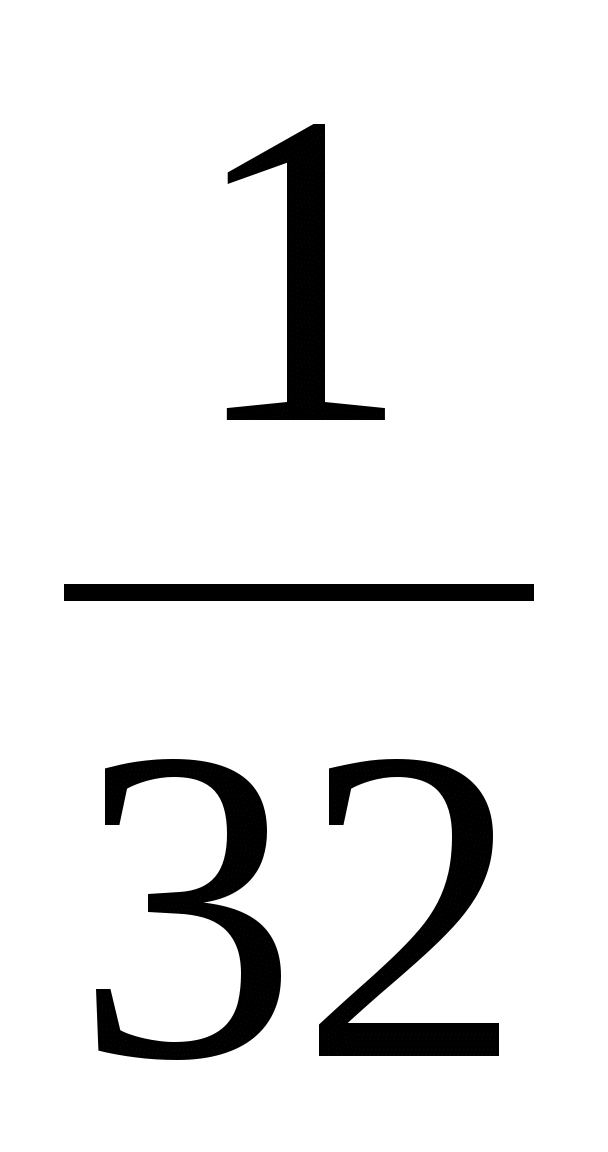 D)
D) 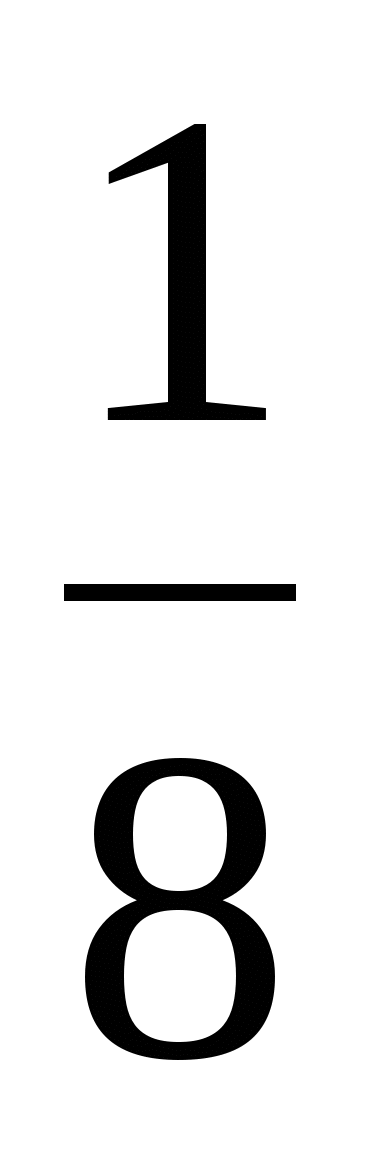 E) 4
E) 4
16. Түбірлері бойынша квадрат теңдеу құрыңыз: х1=
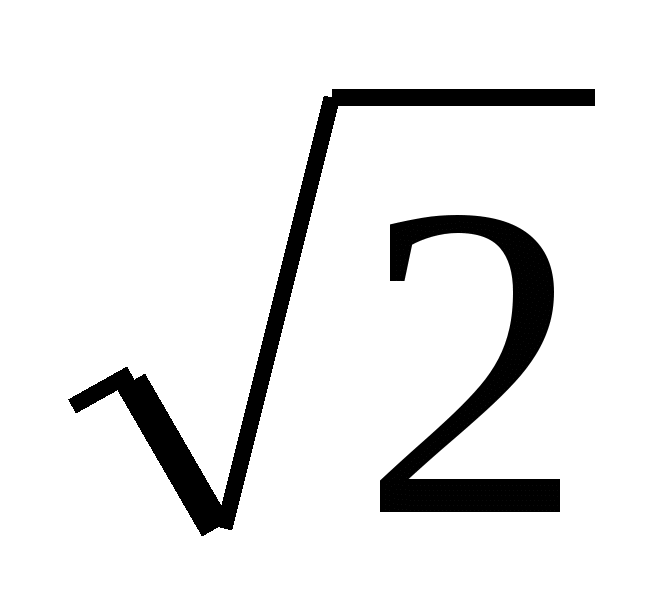 ,
х2 = -
,
х2 = -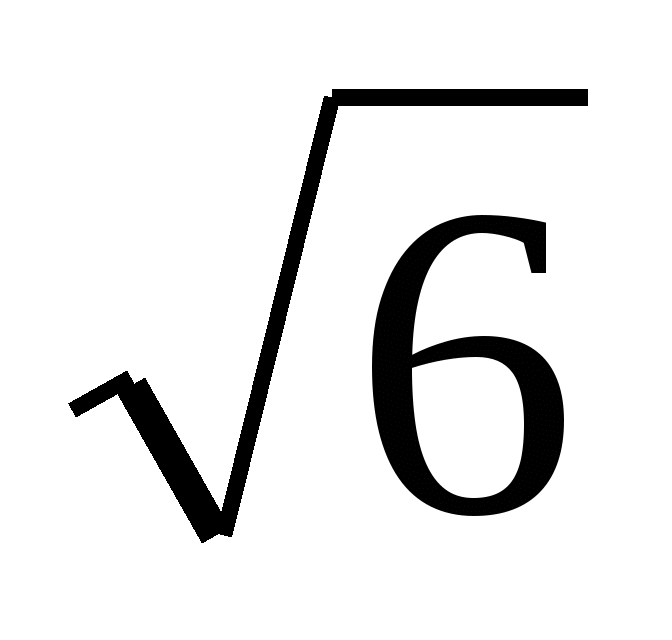 .
.
A) x2 +
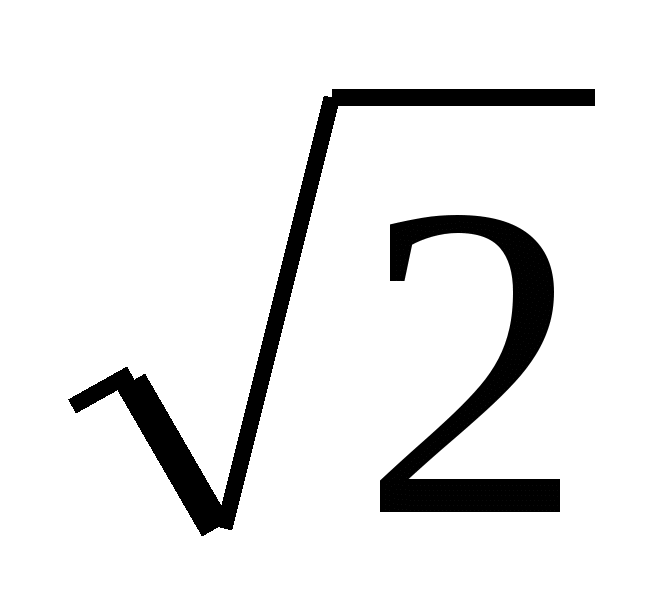 х -
х - 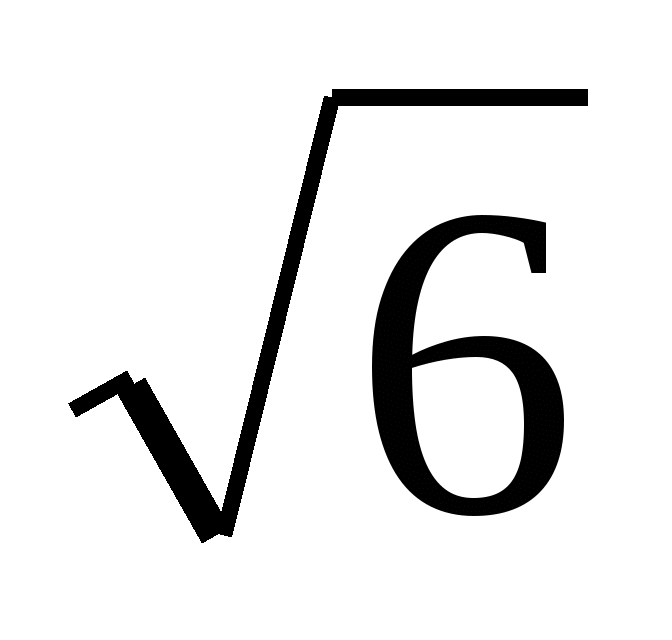 = 0. B) x2 + (
= 0. B) x2 + (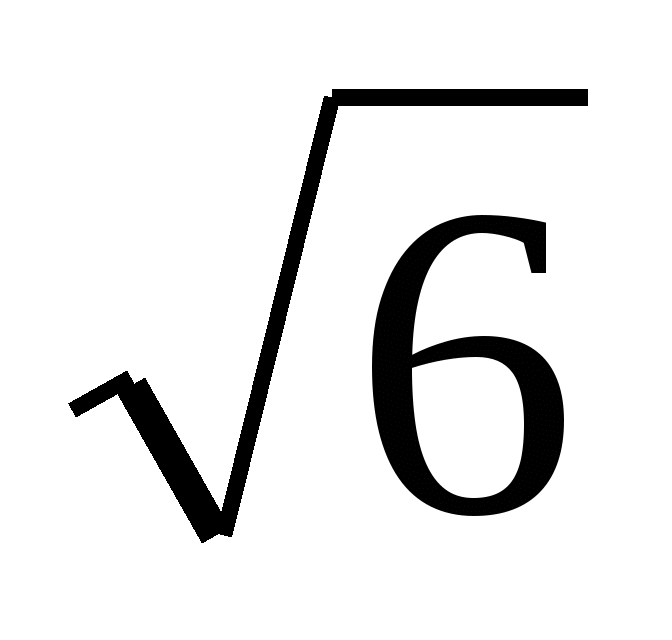 -
- 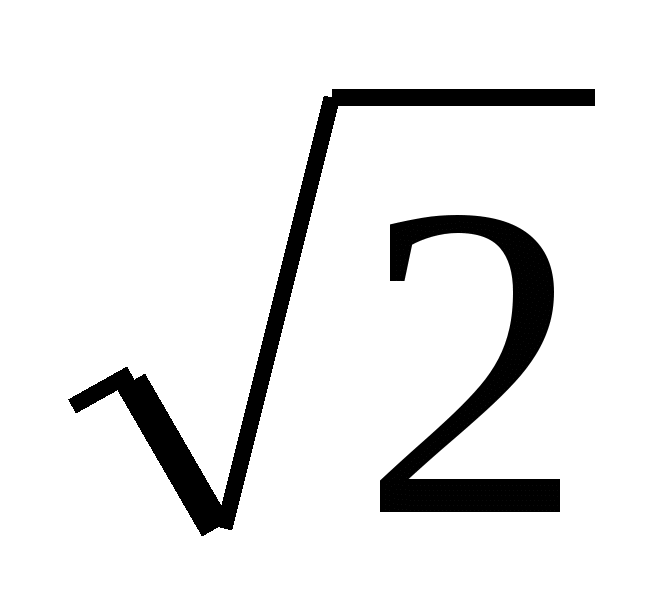 )х - 2
)х - 2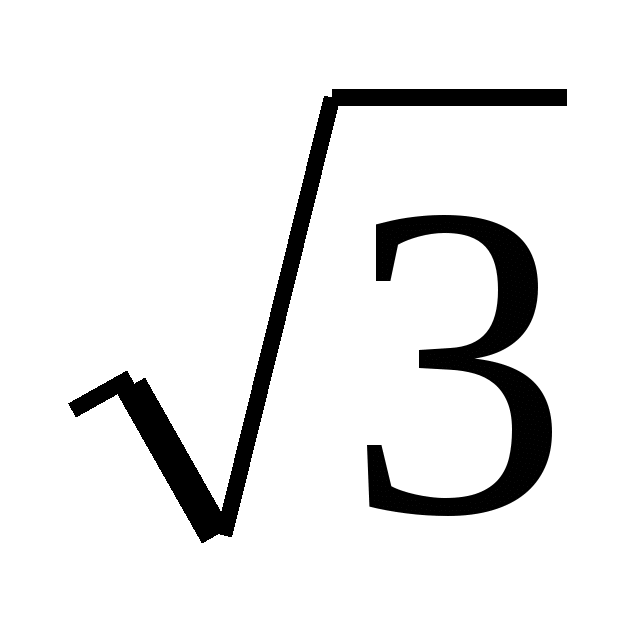 = 0.
= 0.
C) x2 - 5х + 6 = 0. D) x2 +
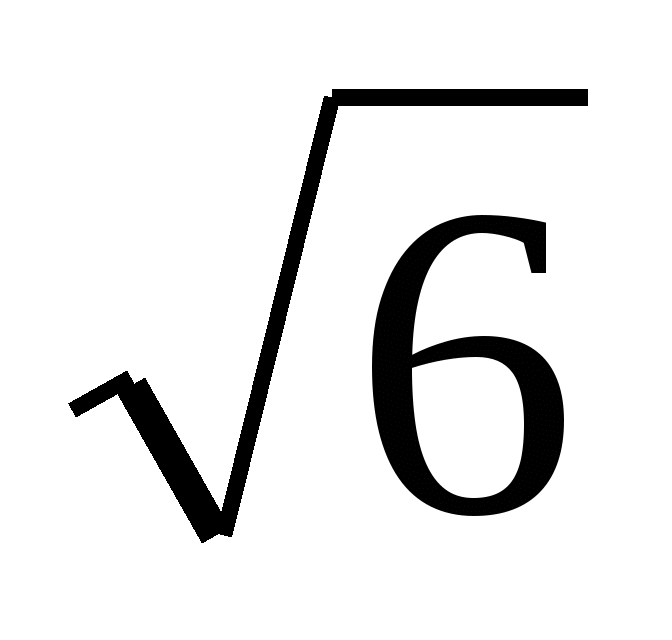 х -
х - 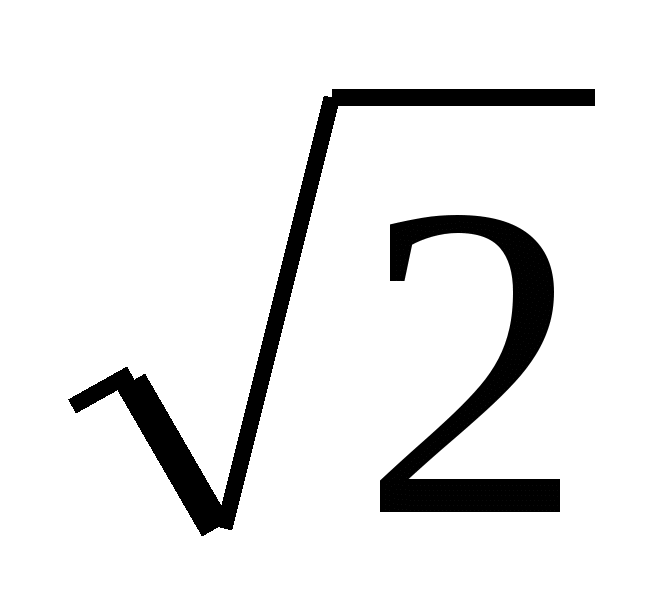 = 0. E) x2 + (
= 0. E) x2 + (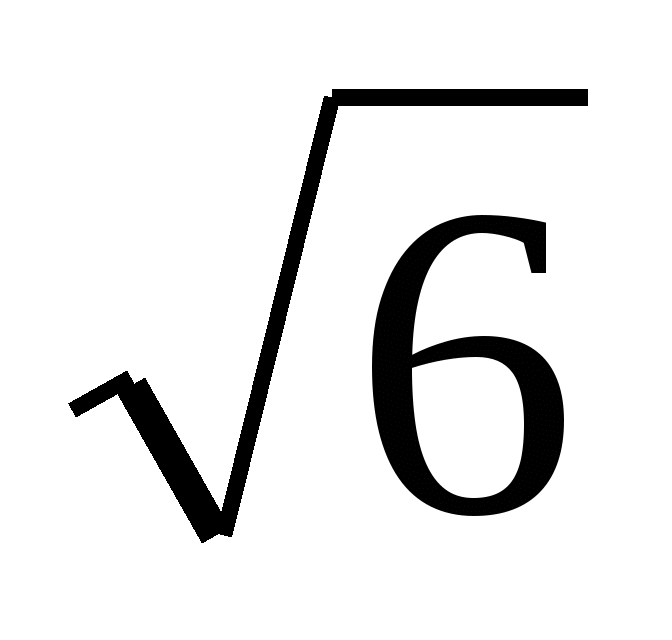 -
- 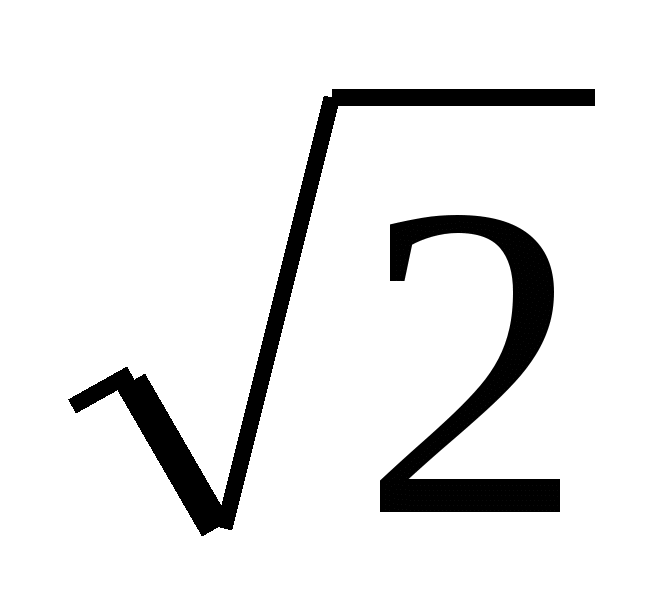 )х + 2
)х + 2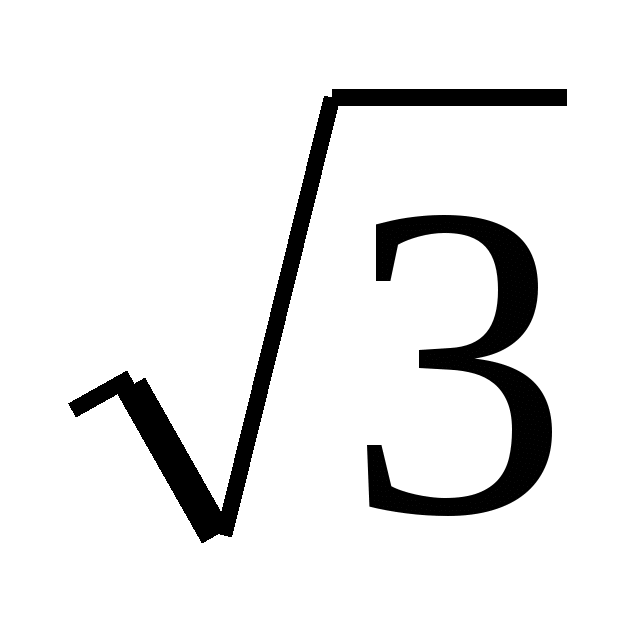 = 0.
= 0.
17. Өрнекті ықшамдаңыздар: (2x + 1 -
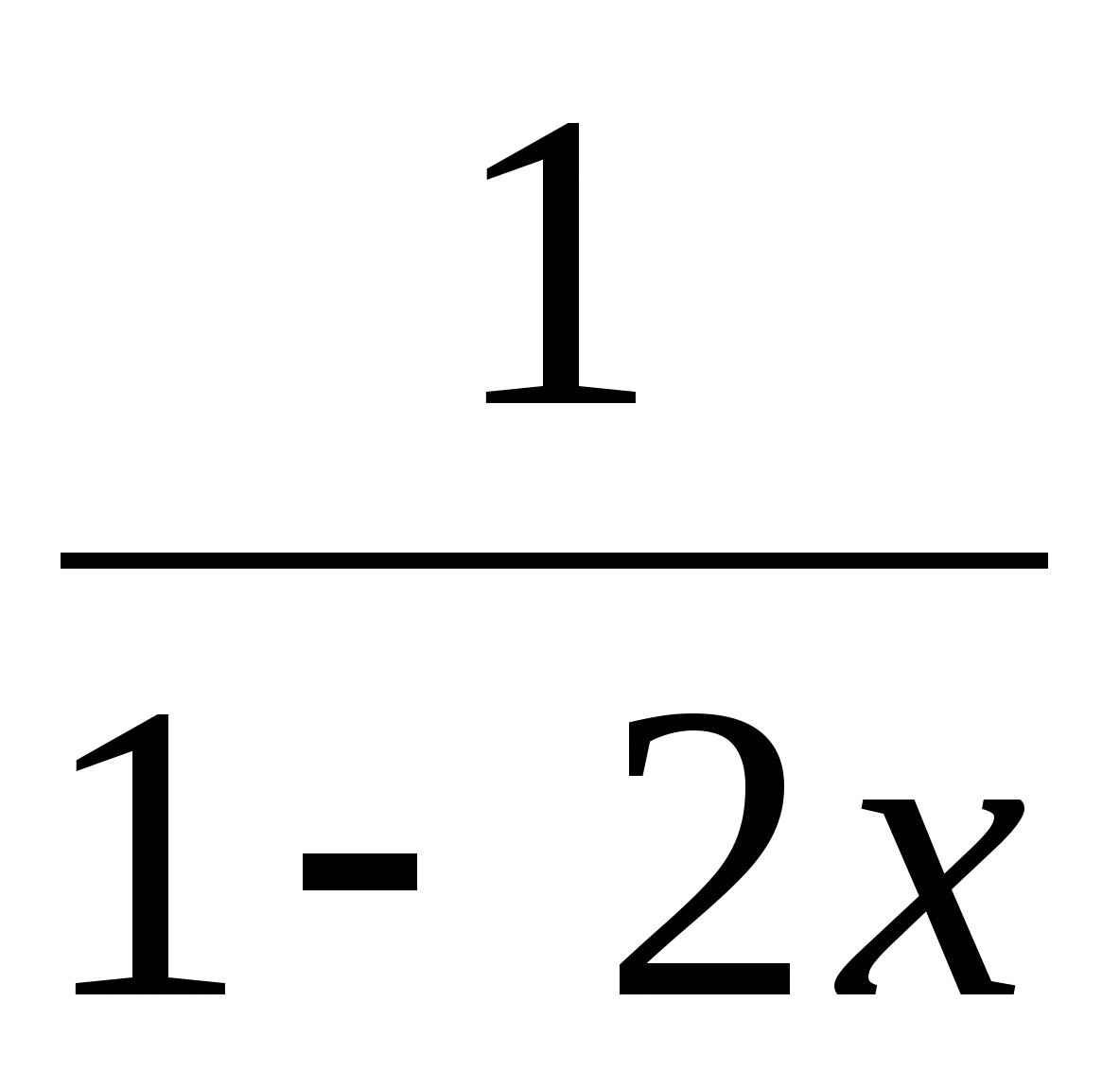 ) : (2x -
) : (2x - 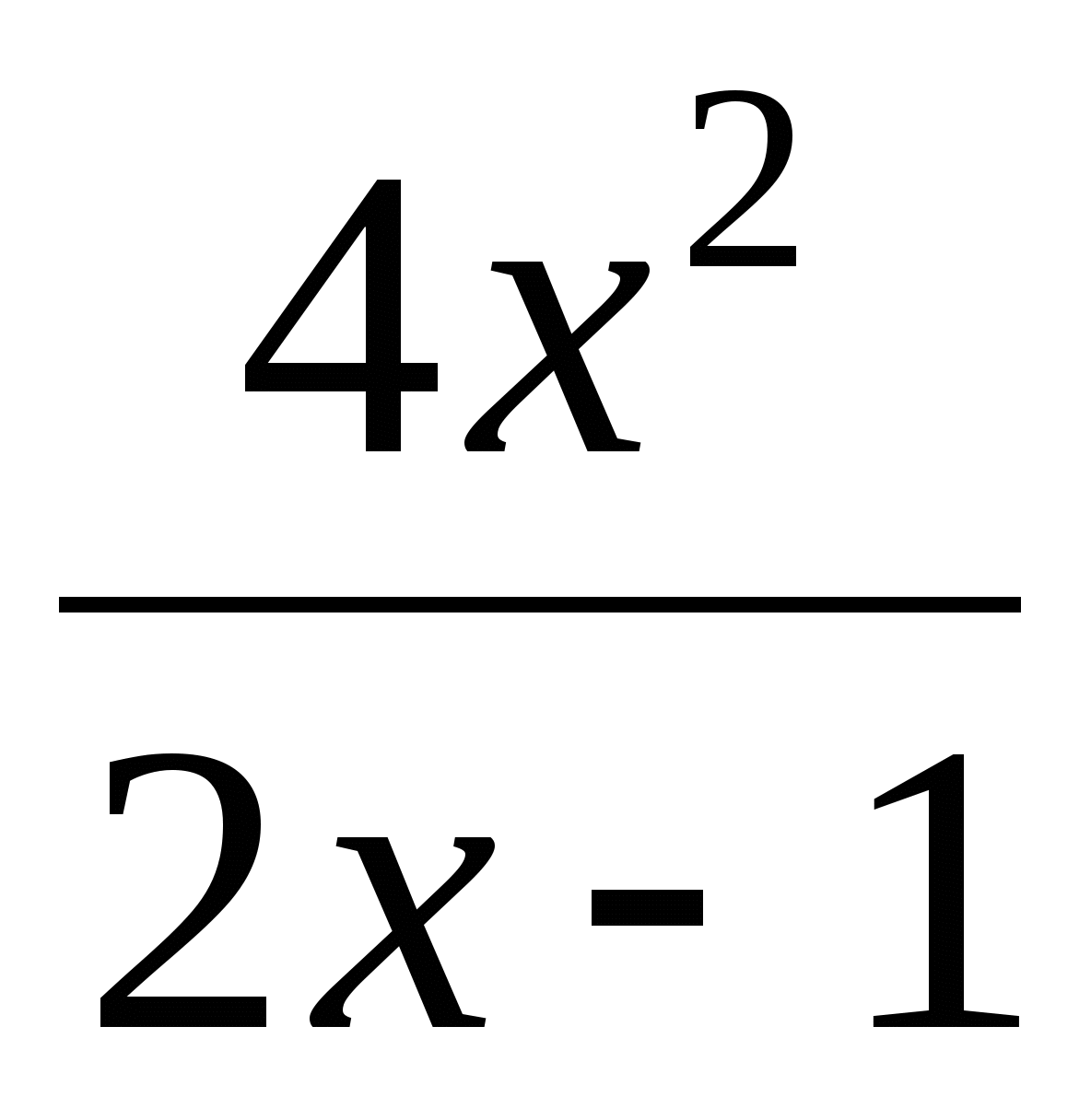 )
)
A) 2x. B) -2x. C) 2x - 1. D) 1 - 2x. E) 5.
18. Көбейткіштерге жіктеңіз: (x2 - x - 1)(y + 2) + (1 + x - x2)(z + 12).
A) (x2 - x - 1)(y + z + 10). B) (x2 + x - 1)(y + z - 10).
C) (x2 - x)(y - z + 9). D) (x2 - x - 1)(y - z - 10).
E) (x2 - x + 1)(y - z - 10).
19. Теңдеулер жүйесін шешіңіз:
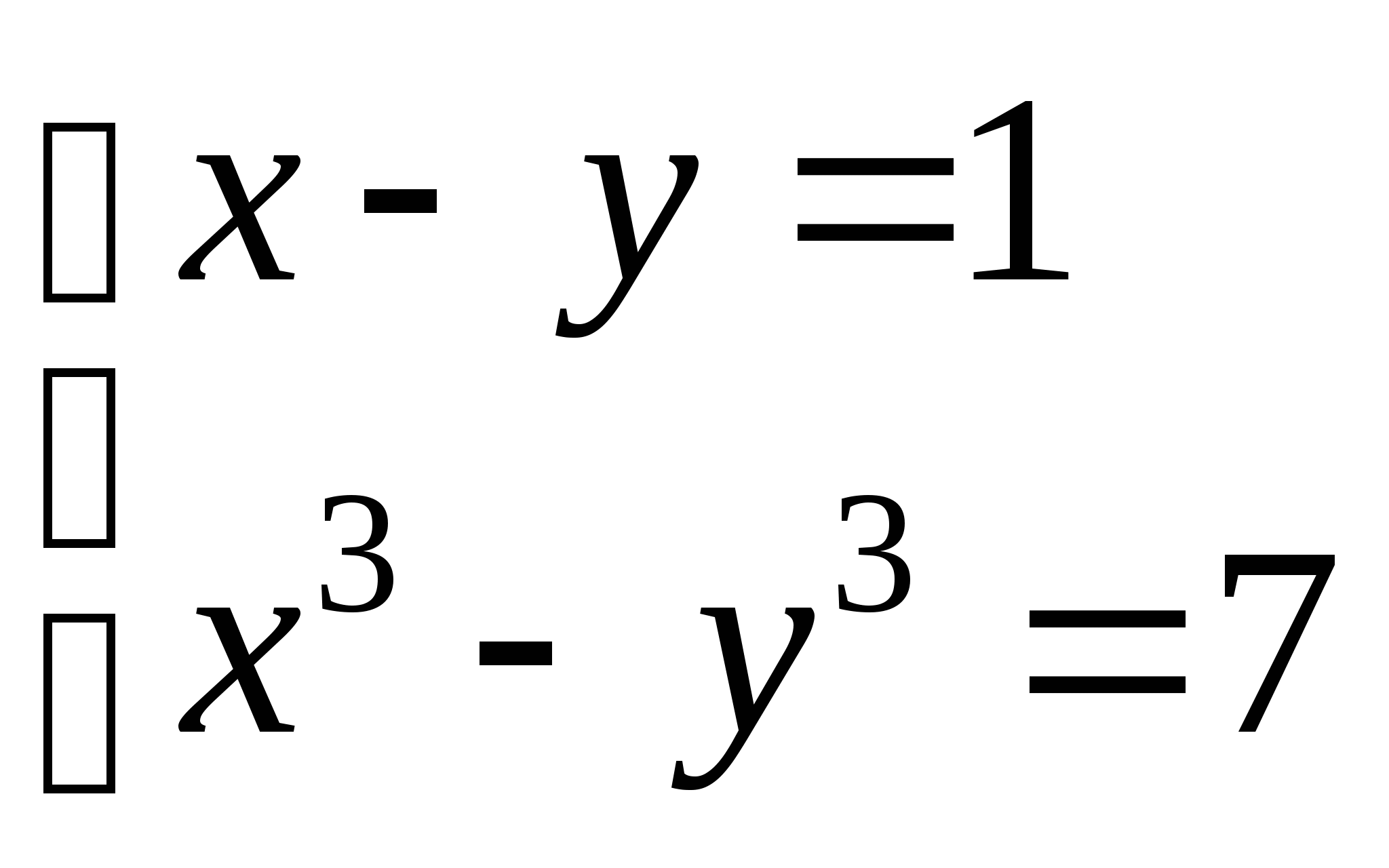 .
.
A) (2; 1), (-1; -2). B) (-2; 1), (-1; 2). C) (-1; 2), (2; -1).
D) (2; -1), (-1; 1). E) (-1; 3), (1; -1).
20. Теңдеулер жүйесін шешіңіз:
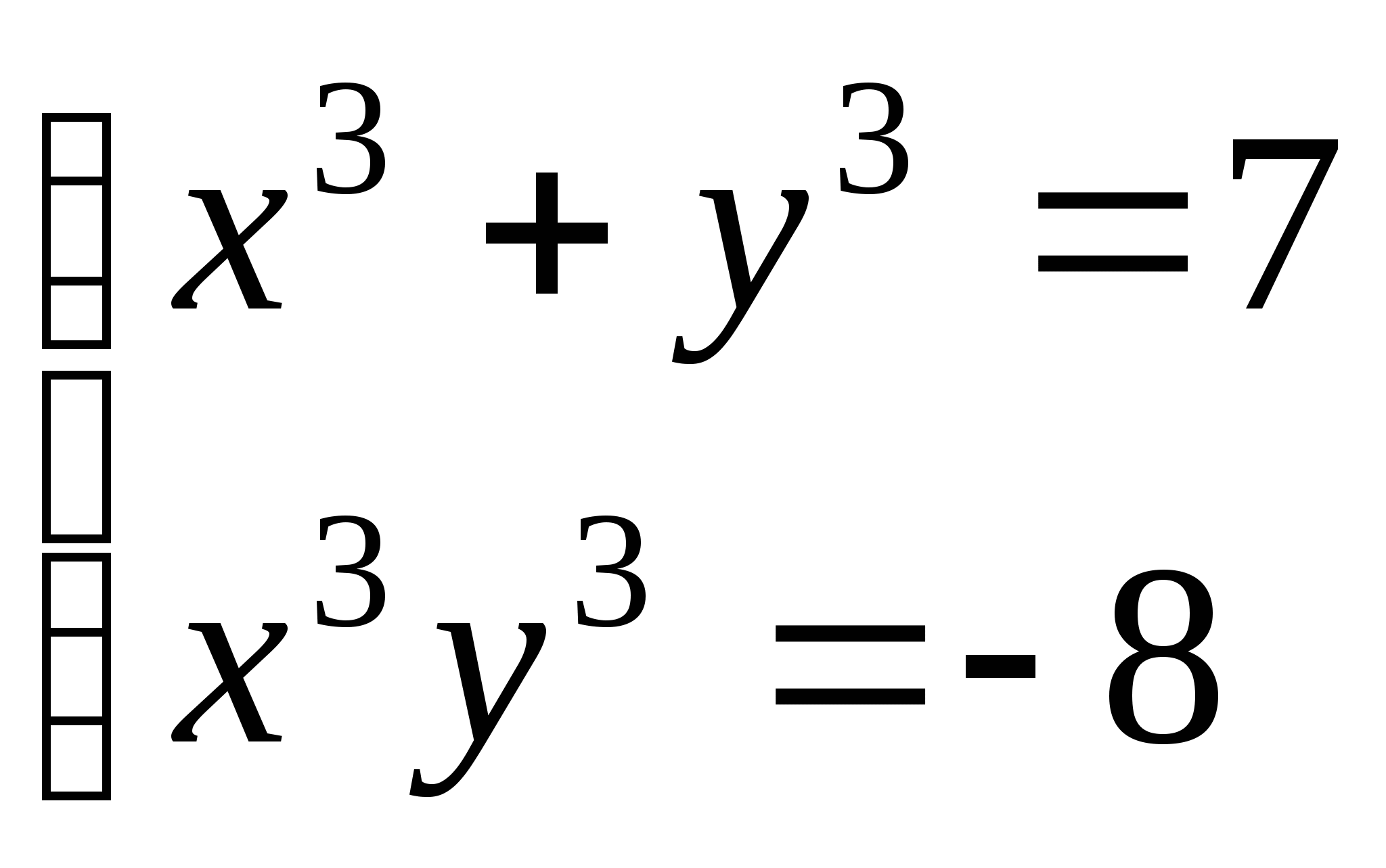
A) (-1; 3), (1; -1) B) (-2; 1), (-1; 2) C) (-1; 2), (2; -1)
D) (2; 1), (-1; -2) E) (2; -1), (-1; 1)
Үйге тапсырма: №20-№25 Қайталау.Өтілген тақырыптарды оқу
Сабақты қорытындылау:
Тригонметриялық функциялар,графигі
Функцияның ең үлкен және ең кіші мәндерін қалай табады?
Экстремум нүктелер дегеніміз не?
Т Ү Й І Н Д Е М Е
 Аты-жөні:
Ескалиева Гулнур Бакытбековна
Аты-жөні:
Ескалиева Гулнур Бакытбековна
Е-mail: eskaliev.erbol@mail.ru</</p>
Жалпы ақпарат:
Туған жылы: 1984 жылғы 7 сәуір
Ұлты: қазақ
Жынысы: әйел
Азаматтығы: Қазақстан Республикасы
Мекен-жайы: Қызылорда облысы, Әйтеке би кенті,С.Аманов көшесі №21 үй
Білімі: Жоғары
2001-2005 ж.ж Қорқыт ата атындағы Қызылорда мемлекеттік университеті
Мамандығы: математика пәні мұғалімі
Жұмыс орны: №266 мектеп-лицей
Қызметі: математика пәнінің мұғалімі
Санаты: екінші
Жалпы еңбек өтілі: 10 жыл
Білім жетілдіру курсынан өткен жылдары, тақырыбы:
2012 ж. Қашықтықтан оқыту курсы «Введение в математику». / Сертификат № 00218087 /- 72сағат
2013 ж. Қызылорда облысы бойынша педогог қызметкерлердің біліктілігін арттыру институтында «Оқу
мен жазу арқылы сын тұрғысынан ойлау технологиясы» - 86 сағат Сертификат №037886
2014 ж. Қызылорда облысы бойынша педогог қызметкерлердің біліктілігін арттыру институты
«Жаратылыстану-математикалық бағытта бейіндік сыныптарда математиканы оқытудың
мазмұны және ұйымдастыру жолдары» - 72 сағат Сертификат №0083611
Мұғалім жетістіктері:
2012 ж. Қарағанды экономикалық Университетінен «Алғыс хат»
2012 ж. Республикалық «45 минут» және «Білімділер» сайтына сабақтарымның электронды нұсқалары
жарияланғаны үшін «Сертификат»
2012 ж. «Сертификат» III,IV Бүкілресейлік қашықтық олимпиадасына оқушылар қатыстырғаным үшін
2014 ж. «Сертификат» VI,VII, VIII Бүкілресейлік қашықтық олимпиадасына оқушылар қатыстырғаным үшін
2014 ж. «Сертификат» «Үздік нәтиже» Қазақстандық интернет олимпиада
2014 ж. «Алғыс хат» мектепшілік
Оқушылардың жетістіктері:
2012 ж. IV Бүкілресейлік қашықтық олимпиадасында 5 сыныптағы 16 оқушым математика пәні бойынша
«III дәрежелі дипломмен» марапатталды
2012 ж. Мектепшілік пән олимпиадасында 5 «В» сынып оқушысы Құрманбай Ержан III орын иеленді
2013 ж. IX Халықаралық олимпиадасында 5 сыныптағы 16 оқушым математика пәні бойынша «I дәрежелі
дипломмен» марапатталды. 11 оқушы «Алтын медаль» иеленді.
2014 ж. Мектепшілік пән олимпиадасында 9 «Г» сынып оқушысы Қаратай Жансая III орын иеленді
2014 ж. VI Бүкілресейлік қашықтық олимпиадасында 6 сыныптағы 3 оқушым математика пәні бойынша
«I дәрежелі дипломмен» марапатталды
2014 ж. Қазақстандық интернет олимпиадаға 10 оқушым қатысып, «Сертификат» иеленді
2014 ж. «Үздік нәтиже» «Сертификат» Қазақстандық интернет олимпиададан 9 «Г» сынып оқушысы
Сайлаубай Назерке иеленді
2014 ж. . «II дәрежелі диплом» «Күміс жүлдеге сай» сертификатымен Қазақстандық интернет
олимпиададан 6 «В» сынып оқушысы Қожаберген Ғазиз марапатталды
2014 ж. VII Бүкілресейлік қашықтық олимпиадасында 6 «В» сынып оқушысы Серикпай Асылзат
математика пәні бойынша «II дәрежелі дипломмен» марапатталды
2014 ж. Мектепшілік пән олимпиадасында 5 «Г» сынып оқушысы Нұрғабылова Мерей II орын, 7 «Д» сынып
оқушысы Тоғымова Әсел I орын, 10 «Г» сынып оқушысы Рахман Мұхтар I орын иеленді.
2014 ж. «Ақбота» интеллектуалдық марафонына 5 «Г» сыныбының 6 оқушысы қатысып, «Сертификат»иеленді
2014 ж. XI Халықаралық олимпиадасы I турынан 5 «Г» сынып оқушысы Нұрғабылова М «Сертификат»иеленді
Баспасөзге жарияланған мақалалары:
2012 ж. Республикалық «Математика Қазақстан мектебінде» ғылыми-әдістемелік журналына «Пәнаралық
есептер және оларға қойылатын талаптар» атты мақалам жарияланды. №5(41 )-2012ж.28 бет
2012 ж. «Ұрпақ тәрбиесі және Интернет мүмкіндігімен Ұстаздардың білімін жетілдіру жолдары»
тақырыбында өткізілген семинарда баяндамам жинаққа енді.
Баяндамалар жинағы,26бет,Қызылорда қаласы
Тілді білуі: Қазақша - ана тілі, орысша - еркін, ағылшынша-сөздікпен
Жеке қасиеттері: Жан-жақтылық, ұйымдастырушылық, көпшілдік.
Құштарлығым: Көркем әдебиет оқу
Білім жетілдіру курсынан өткен жылдары, тақырыбы:
2012 ж. Қашықтықтан оқыту курсы «Введение в математику». / Сертификат № 00218087 /- 72сағат
2013 ж. Қызылорда облысы бойынша педогог қызметкерлердің біліктілігін арттыру институтында «Оқу
мен жазу арқылы сын тұрғысынан ойлау технологиясы» - 86 сағат Сертификат №037886
2014 ж. Қызылорда облысы бойынша педогог қызметкерлердің біліктілігін арттыру институты
«Жаратылыстану-математикалық бағытта бейіндік сыныптарда математиканы оқытудың
мазмұны және ұйымдастыру жолдары» - 72 сағат Сертификат №0083611
2013 жылы
«Оқу мен жазу арқылы сын тұрғы-
сынан ойлау технологиясы»
72 сағат
2014 ж.жылы
«Жаратылыстану-математикалық
бағытта бейіндік сыныптарда
математиканы оқытудың мазмұны
және ұйымдастыру жолдары»
- 72 сағат Сертификат №0083611
Мұғалім жетістіктері:
2012 ж. Қарағанды экономикалық Университетінен «Алғыс хат»
2012 ж. Республикалық «45 минут» және «Білімділер» сайтына сабақтарымның электронды нұсқалары
жарияланғаны үшін «Сертификат»
2012 ж. «Сертификат» III,IV Бүкілресейлік қашықтық олимпиадасына оқушылар қатыстырғаным үшін
2014 ж. «Сертификат» VI,VII, VIII Бүкілресейлік қашықтық олимпиадасына оқушылар қатыстырғаным үшін
2014 ж. «Сертификат» «Үздік нәтиже» Қазақстандық интернет олимпиада
2014 ж. «Алғыс хат» мектепшілік
Баспасөзге жарияланған мақалалары:
2012 ж. Республикалық «Математика Қазақстан мектебінде» ғылыми-әдістемелік журналына «Пәнаралық
есептер және оларға қойылатын талаптар» атты мақалам жарияланды. №5(41 )-2012ж.28 бет
2012 ж. «Ұрпақ тәрбиесі және Интернет мүмкіндігімен Ұстаздардың білімін жетілдіру жолдары»
тақырыбында өткізілген семинарда баяндамам жинаққа енді.
Баяндамалар жинағы,26бет,Қызылорда қаласы
Оқушылардың
жетістіктері:
2012 ж. IV Бүкілресейлік қашықтық олимпиадасында 5 сыныптағы 16 оқушым математика пәні бойынша
«III дәрежелі дипломмен» марапатталды
2012 ж. Мектепшілік пән олимпиадасында 5 «В» сынып оқушысы Құрманбай Ержан III орын иеленді
2013 ж. IX Халықаралық олимпиадасында 5 сыныптағы 16 оқушым математика пәні бойынша «I дәрежелі
дипломмен» марапатталды. 11 оқушы «Алтын медаль» иеленді.
2014 ж. Мектепшілік пән олимпиадасында 9 «Г» сынып оқушысы Қаратай Жансая III орын иеленді
2014 ж. VI Бүкілресейлік қашықтық олимпиадасында 6 сыныптағы 3 оқушым математика пәні бойынша
«I дәрежелі дипломмен» марапатталды
2014 ж. Қазақстандық интернет олимпиадаға 10 оқушым қатысып, «Сертификат» иеленді
2014 ж. «Үздік нәтиже» «Сертификат» Қазақстандық интернет олимпиададан 9 «Г» сынып оқушысы
Сайлаубай Назерке иеленді
2014 ж. . «II дәрежелі диплом» «Күміс жүлдеге сай» сертификатымен Қазақстандық интернет
олимпиададан 6 «В» сынып оқушысы Қожаберген Ғазиз марапатталды
2014 ж. VII Бүкілресейлік қашықтық олимпиадасында 6 «В» сынып оқушысы Серикпай Асылзат
математика пәні бойынша «II дәрежелі дипломмен» марапатталды
2014 ж. Мектепшілік пән олимпиадасында 5 «Г» сынып оқушысы Нұрғабылова Мерей II орын, 7 «Д» сынып
оқушысы Тоғымова Әсел I орын, 10 «Г» сынып оқушысы Рахман Мұхтар I орын иеленді.
2014 ж. «Ақбота» интеллектуалдық марафонына 5 «Г» сыныбының 6 оқушысы қатысып, «Сертификат»иеленді
2014 ж. XI Халықаралық олимпиадасы I турынан 5 «Г» сынып оқушысы Нұрғабылова М «Сертификат»иеленді