Нестандартные задачи по математике с решениями. 7-9 класс. Часть 2.

Интерес к математике и математические способности учащихся проявляются в довольно раннем возрасте. Значительную роль в их развитии играет систематическое решение задач, которые могли бы заинтересовать юных математиков и способствовали бы стремлению к самостоятельным исследованиям.

Именно такие задачи содержит данный сборник. Он предназначен для внеклассных занятий с учащимися 7-9 классов.

В сборнике приведены подробные решения 20 нестандартных задач. Многие из них предлагались на математических олимпиадах.

Данный сборник может служить пособием для подготовки учащихся к олимпиадам по математике.

Задача № 1

Доказать равенство

Решение:

Задача № 2

Доказать, что выражение не равно нулю, если a, b, c - попарно не равные между собой числа.

Решение:

=

т.к. a.

Задача № 3

Доказать, что делится на 6 при любом натуральном n.

Решение:

это произведение трех последовательных чисел, поэтому делится на 1.

12n делится на 6 очевидно. Следовательно, делится на 6, поэтому делится на 6.

Задача № 4

Доказать, что число делится на 3 при любом натуральном n.

Решение:

- три последовательных числа, значит делится на 3.

также делится на3. Следовательно, делится на 3, поэтому делится на 3.

Задача № 5

Доказать, что если n - натуральное число и n , то составное число.

Решение:

Так как n - натуральное, то - целые числа, не равные 1. Значит, - составное число.

Задача № 6

Доказать равенство:

Решение:

Задача № 7

Доказать равенство:

Решение:

=

Задача № 8

Доказать равенство:

Решение:

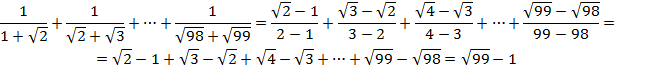
Задача № 9

Доказать равенство:

Решение:

Задача № 10

Доказать равенство:

Решение:

Задача № 11

Доказать, что число является квадратом некоторого натурального числа x, и найти x.

Решение:

Пусть 1980

Значит, x =

Задача № 12

Упростить выражение:

Решение:

Задача № 13

Упростить выражение:

Решение:

Задача № 14

Упростить выражение: ,если

Решение:

Если , то B=

Задача № 15

Упростить выражение: , если , где

Решение:

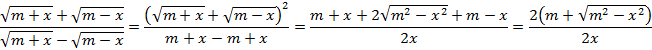
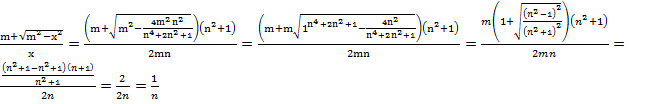Если , то при

Задача № 16

Найти все значения r, при которых уравнение имеет:

1) равные корни;

2) корни, модули которых равны, а знаки противоположны.

Решение:

1) Уравнение будет иметь равные корни при D=0.

2) Уравнение будет иметь корни, модули которых равны, а знаки противоположны, если второй коэффициент будет равен 0 и это уравнение станет неполным. Значит, при r=0 уравнение примет вид .

Задача № 17

Доказать что если , то квадратное уравнение . Имеет действительные корни. При каких значениях оба корня этого уравнения отрицательные?

Решение:

1) Докажем ,что данное уравнение имеет действительные корни при

Уравнение будет иметь действительные корни, если . Но данный дискриминант будет равен нулю при , а по условию , значит, этот дискриминант должен быть строго больше нуля. Он больше нуля, т.к.. Значит, уравнениеимеет действительные корни.

2) Чтобы уравнение имело два отрицательных корня, свободный коэффициент должен быть с положительным знаком, т.к. , а их сумма равна отрицательному числу.

Решим систему неравенств:

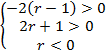
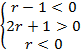
Ответ:

Задача № 18

Каким условиям удовлетворяют числа a и b ,если биквадратное уравнение имеет четыре различных действительных корня?

Решение:

Так как уравнение имеет 4 различных корня, то k и -положительны, т.к. ,. Уравнение будет иметь положительные корни при и при положительном дискриминанте.

Сумма двух чисел будет положительна, только если эти оба числа будут положительны, значит

Ответ:

Задача № 19

Какой цифрой оканчивается число

Решение:

оканчивается цифрой 2.

оканчивается цифрой 4.

оканчивается цифрой 8.

оканчивается цифрой 6.

оканчивается цифрой 2.

оканчивается цифрой 4.

………………………………………..

Т.е. через каждые четыре показателя числа будут оканчиваться теми же цифрами. Так как при делении 1982 на 4 получаем в остатке 2, то число оканчивается той же цифрой, что , т.е. цифрой 4.

Задача № 20

Пусть . Доказать что .

Решение: