Муниципальное образовательное учреждение

Новоилимская общеобразовательная школа имени Н.И. Черных

Рабочая программа составлена основе следующих нормативно - правовых документов:

1. Федеральный компонент государственного стандарта (основного общего образования) по математике, утвержден приказом Минообразования России от 05.03.2004 г. № 1089

2. Федеральный государственный стандарт основного общего образования, утвержден приказом Министерства образования и науки Российской Федерации от 17 декабря 2010 г. № 1897.

3. Закон Российской Федерации «Об образовании» (статья 7).

4. Региональный учебный план для образовательных учреждений Иркутской области, реализующих программы начального общего, основного общего и среднего (полного) общего образования (далее РУП) на 2011-2012, 2012-2013, учебные годы от 12.08.2011г. № 920-мр;

5. Учебный план ОУ «Новоилимская средняя общеобразовательная школа имени Н.И. Черных» на 2016-2017 учебный год;

6. Программы для общеобразовательных школ, гимназий, лицеев: Математика 5-11 кл./ Сост. Г.М. Кузнецова, Н.Г. Миндюк; 4-е изд. - 2004 г.

7. Письмо службы по контролю и надзору в сфере образования Иркутской области от 15.04.2011 № 75-37-0541/11.

Пояснительная записка.

Общая характеристика учебного предмета.

Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.

Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.

Алгебра Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышле­ния, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.

Геометрия - один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, фор­мирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математи­ческой культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.

Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности - умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.

При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации, и закладываются основы вероятностного мышления.

Таким образом, в ходе освоения содержания курса учащиеся получают возможность:

развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;

получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;

развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

В курсе алгебры 9 класса вырабатывается умение раскладывать квадратный трехчлен на множители; умение строить график функции у = ах² + bх + с, умение указывать координаты вершины параболы, оси симметрии, направление ветвей; умение находить по графику промежутки возрастания и убывания функции, промежутки, в которых функция сохраняет знак; умение решать неравенства вида ах² + bх + с>0 или ах² + bх + с<0, где а0; умение решать целые и дробно рациональные уравнения с одной переменной; умение решать простейшие системы, содержащие уравнение второй степени с двумя переменными, и текстовые задачи с помощью составления таких систем; вырабатывается умение использовать индексное обозначение, которое используется при изучении арифметической и геометрической прогрессии; умение использовать комбинаторное правила умножения, которое используется при выводе формул для подсчета числа перестановок, размещений и сочетаний, умение определять, о каком виде комбинаций идет речь в задаче.

Цель изучения курса:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;

• развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники), усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников. В ходе изучения курса учащиеся овладевают приёмами вычислений на калькуляторе.

Задачи курса:

-ввести понятия квадратного трехчлена, корня квадратного трехчлена, изучить формулу разложения квадратного трехчлена на множители;

- расширить сведения о свойствах функций, познакомить со свойствами и графиком квадратичной функции и степенной функции;

- систематизировать и обобщить сведения о решении целых и дробных рациональных уравнений с одной переменной ;

- научить решать квадратичные неравенства;

- завершается изучение систем уравнений с двумя переменными;

- вводится понятие неравенства с двумя переменными и системы неравенств с двумя переменными;

- вводится понятие последовательности, изучается арифметическая и геометрическая прогрессии;

- ввести элементы комбинаторики и теории вероятностей.

Место предмета в учебном плане

Согласно Федеральному базисному учебному плану на изучение математики в 9 классе отводится не менее 170 часов из расчета 5 ч в неделю, при этом разделение часов на изучение алгебры и геометрии следующее: 3 часа в неделю алгебры, итого 102 часа; 2 часа в неделю геометрии, итого 68 часов.

Используемые технологии, методы и формы работы.

При реализации данной программы используются элементы следующих технологий: личностно ориентированное обучение, дифференцированное обучение.

Методы обучения

1. Классификация по источнику знаний:

   • Словесные

   • Наглядные

   • Практические

2. Классификация по характеру УПД

   • Объяснительно-иллюстративный

   • Проблемное изложение знаний

   • Частично-поисковый (эвристический)

   • Исследовательский

   • Репродуктивный

3. Классификация по логике

   • Индуктивный

   • Дедуктивный

   • Аналогии

Для продуктивной работы по данной программе следует сочетать многообразие методов обучения.

Формы работы

К наиболее приемлемым формам организации учебных занятий по математике можно отнести:

Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи.

Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, практическое применение различных методов решения задач. Комбинированный урок предполагает выполнение работ и заданий разного вида.

Урок-игра. На основе игровой деятельности учащиеся познают новое, закрепляют изученное, отрабатывают различные учебные навыки.

Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке.

Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня обученности учащихся, тренировки технике тестирования.

Урок - самостоятельная работа. Предлагаются разные виды самостоятельных работ.

Урок - контрольная работа. Контроль знаний по пройденной теме

Требования к уровню подготовки обучающихся в 9 классе.

В ходе преподавания алгебры в 9 классе, работы над формированием у обучающихся перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:

планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;

решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;

ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;

проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;

поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

В результате изучения курса алгебры обучающиеся должны:

знать/понимать¹

• существо понятия математического доказательства; примеры доказательств;

• существо понятия алгоритма; примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов,;

• каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

Арифметика

уметь

• выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;

• переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты - в виде дроби и дробь - в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;

• выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;

• округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;

• пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;

• решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;

• устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;

• интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;

Алгебра

уметь

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

• применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;

• решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;

• решать линейные и квадратные неравенства с одной переменной и их системы;

• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• изображать числа точками на координатной прямой;

• определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;

• распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;

• описывать свойства изученных функций (у=кх, где к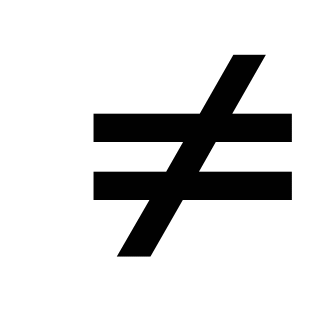0, у=кх+b, у=х², у=х³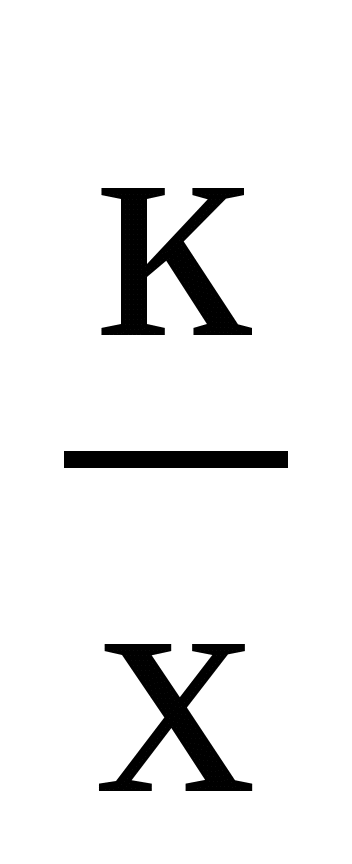, у =, у=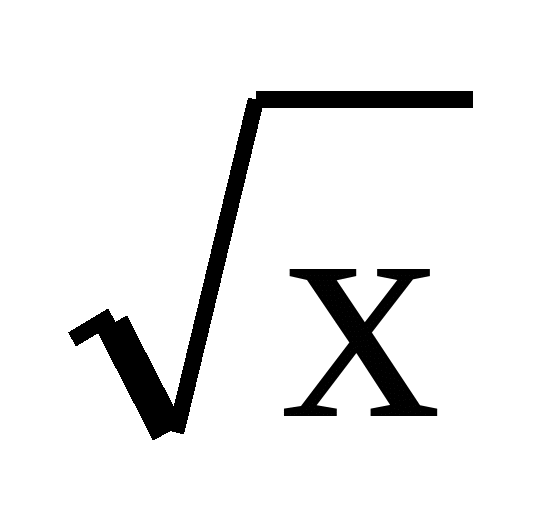), строить их графики;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;

• описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между величинами.

Элементы логики, комбинаторики,

статистики и теории вероятностей

уметь

• проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;

• извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;

• решать комбинаторные задачи путем систематического перебора возможных вариантов, вычислять средние значения результатов измерений;

• находить частоту события, используя собственные наблюдения и готовые статистические данные;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выстраивания аргументации при доказательстве (в форме монолога и диалога);

• распознавания логически некорректных рассуждений;

• записи математических утверждений, доказательств;

• анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;

• решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;

• решения учебных и практических задач, требующих систематического перебора вариантов;

• понимания статистических утверждений.

Содержание обучения:

Глава 1. Свойства функций. Квадратичная функция (22 часа)

Функция. Свойства функций. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Функция у = ах² + bх + с, её свойства и график. Степенная функция.

Цель: расширить сведения о свойствах функций, ознакомить обучающихся со свойствами и графиком квадратичной функции.

В начале темы систематизируются сведения о функциях. Повторяются основные понятия: функция, аргумент, область определения функции, график. Даются понятия о возрастании и убывании функции, промежутках знакопостоянства. Тем самым создается база для усвоения свойств квадратичной и степенной функций, а также для дальнейшего углубления функциональных представлений при изучении курса алгебры и начал анализа.

Подготовительным шагом к изучению свойств квадратичной функции является также рассмотрение вопроса о квадратном трехчлене и его корнях, выделении квадрата двучлена из квад­ратного трехчлена, разложении квадратного трехчлена на множители.

Изучение квадратичной функции начинается с рассмотрения функции у=ах², её свойств и особенностей графика, а также других частных видов квадратичной функции - функции у=ах²+n, у=а(х-m)². Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы обучающиеся поняли, что график функции у = ах² + bх + с может быть получен из графика функции у = ах² с помощью двух параллельных переносов. Приёмы построения графика функции у = ах² + bх + с отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у обучающихся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы.

При изучении этой темы дальнейшее развитие получает умение находить по графику промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет знак.

Учащиеся знакомятся со свойствами степенной функции у=хⁿ при четном и нечетном натуральном показателе n.. Вводится понятие корня n-й степени. Обучающиеся должны понимать смысл записей вида , . Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.

Глава 2. Уравнения и системы уравнений (14 часов)

Целые уравнения. Дробные рациональные уравнения. Неравенства второй степени с одной переменной. Метод интервалов.

Цель: систематизировать и обобщить сведения о решении целых и дробных рациональных уравнений с одной переменной, сформировать умение решать неравенства вида ах² + bх + с>0 или ах² + bх + с<0, где а0.

В этой теме завершается изучение рациональных уравнений с одной переменной. В связи с этим проводится некоторое обобщение и углубление сведений об уравнениях. Вводятся понятия целого рационального уравнения и его степени. Учащиеся знакомятся с решением уравнений третьей степени и четвертой степени с помощью разложения на множители и введения вспомогательной переменной. Метод решения уравнений путем введения вспомогательных переменных будет широко использоваться дальнейшем при решении тригонометрических, логарифмических и других видов уравнений.

Расширяются сведения о решении дробных рациональных уравнений. Учащиеся знакомятся с некоторыми специальными приемами решения таких уравнений.

Формирование умений решать неравенства вида ах² + bх + с>0 или ах² + bх + с<0, где а0, осуществляется с опорой на сведения о графике квадратичной функции (направление ветвей, ее расположение относительно оси Ох).

Учащиеся знакомятся с методом интервалов, с помощью которого решаются несложные рациональные неравенства.

Глава 3. Уравнения и неравенства с двумя переменными. (17часов).

Уравнение с двумя переменными и его график. Системы уравнений второй степени. Решение задач с помощью систем уравнений второй степени. Неравенства с двумя переменными и их системы.

Цель: вырабатывать умение решать простейшие системы, содержащие уравнение второй степени с двумя переменными, и текстовые задачи с помощью составления таких систем.

В данной теме завершаемся изучение систем уравнений с двумя. переменными. Основное внимание уделяется системам, в которых одно из уравнений первой степени, а другое второй. Известный учащимся способ подстановки находит здесь дальнейшее применение и позволяет сводить решение таких систем к решению квадратного уравнения.

Ознакомление обучающихся с примерами систем уравнений с двумя переменными, в которых оба уравнения второй степени, должно осуществляться с достаточной осторожностью и ограни­чиваться простейшими примерами.

Привлечение известных обучающимся графиков позволяет привести примеры графического решения систем уравнений. С помощью графических представлений можно наглядно показать обучающимся, что системы двух уравнений с двумя переменными второй степени могут иметь одно, два, три, четыре решения или не иметь решений.

Разработанный математический аппарат позволяет существенно расширить класс содержательных текстовых задач, решаемых с помощью систем уравнений.

Изучение темы завершается введением понятия неравенства и системы неравенств с двумя переменными. Сведения о графиках уравнений с двумя переменными используется при иллюстрации множеств решений некоторых простейших неравенств с двумя переменными и их систем.

Глава 4. Арифметическая и геометрическая прогрессии (15 часов)

Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы первых n членов прогрессии. Бесконечно убывающая геометрическая прогрессия.

Цель: дать понятия об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.

При изучении темы вводится понятие последовательности, разъясняется смысл термина «n-й член последовательности», вырабатывается умение использовать индексное обозначение. Эти сведения носят вспомогательный характер и используются для изучения арифметической и геометрической прогрессий.

Работа с формулами n-го члена и суммы первых n членов прогрессий, помимо своего основного назначения, позволяет неоднократно возвращаться к вычислениям, тождественным преобразованиям, решению уравнений, неравенств, систем.

Рассматриваются характеристические свойства арифметической и геометрической прогрессий, что позволяет расширить круг предлагаемых задач.

Глава 5. Элементы комбинаторики и теории вероятностей (13 часов)

Комбинаторное правило умножения. Перестановки, размеще­ния, сочетания. Относительная частота и вероятность случайного события.

Цель: ознакомить учащихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчета их числа; ввести понятия относительной частоты и вероятности случайного события.

Изучение темы начинается с решения задач, в которых требуется составить те или иные комбинации элементов и. подсчитатьих число. Разъясняется комбинаторное правило умножения, которое исполнятся в дальнейшем при выводе формул для подсчёта числа перестановок, размещений и сочетаний.

При изучении данного материала необходимо обратить внимание обучающихся на различие понятий «размещение» и «сочетание», сформировать у них умение определять, о каком виде комбинаций идет речь в задаче.

В данной теме учащиеся знакомятся с начальными сведениями из теории вероятностей. Вводятся понятия «случайное событие», «относительная частота», «вероятность случайного события». Рассматриваются статистический и классический подходы к определению вероятности случайного события. Важно обратить внимание обучающихся на то, что классическое определение вероятности можно применять только к таким моделям реальных событий, в которых все исходы являются равновозможными.

6. Повторение(27 часов)

Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры основной общеобразовательной школы.

Учебно-тематическое планирование.

По алгебре

Класс 9

Учитель С.Н. Сенюшкина

Количество часов

3 часа в неделю алгебры, итого 102 часа

Плановых контрольных уроков 10

Планирование составлено на основе программы по математике.5-6 классы. Авт. - сост. И.И,Зубарева, А.Г.Мордкович. -М. : Мнемозина, 2007.

Учебник: Алгебра 9. / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова. Под редакцией С.А. Теляковского. / М.: Просвещение, 2008

Отличительные особенности рабочей программы по сравнению с примерной:

В программу внесены изменения: уменьшено или увеличено количество часов на изучение некоторых тем. Сравнительная таблица приведена ниже.

22

22

2. Уравнения и неравенства с одной переменной

14

14

3. Уравнения и неравенства с двумя переменными

17

17

4. Прогрессии

15

15

5. Элементы комбинаторики и теории вероятностей

13

13

6. Повторение

21

21

2

1

Функция. Область определения функции и область значений функции.

2

3

4

2

Свойства функций

2

5

6

3

Квадратный трехчлен и его корни

2

7

8

9

4

Разложение квадратного трехчлена на множители

3

10

Контрольная работа № 1

1

11

12

5

Функция у=ах², ее график и свойства

2

13

14

6

Графики функций у=ах²+n

и у=а(х-m)²

2

15

16

17

18

7

Построение графика квадратичной функции

4

19

8

Функция у=хⁿ

1

20

21

9

Корень n-ой степени

2

22

Контрольная работа № 2

1

Уравнения и неравенства с одной переменной

14

23

24

25

26

12

Целое уравнение и его корни

4

27

28

29

30

13

Дробные рациональные уравнения

4

31

32

14

Решение неравенств второй степени с одной переменной

2

33

34

35

15

Решение неравенств методом интервалов

3

36

Контрольная работа № 3

1

Уравнения и неравенства с двумя переменными

17

37

38

17

Уравнение с двумя переменными и его график

2

39

40

18

Графический способ решения систем уравнений

2

41

42

43

44

19

Решение систем уравнений второй степени

4

45

46

47

48

20

Решение задач с помощью систем уравнений второй степени

4

49

50

21

Неравенства с двумя переменными

2

51

52

22

Системы неравенств с двумя переменными

2

53

Контрольная работа № 4

1

Арифметическая и геометрическая прогрессии

15

54

24

Последовательности

1

55

56

57

25

Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии.

3

58

59

60

26

Формула суммы n первых членов арифметической прогрессии

3

61

Контрольная работа № 5

1

62

63

27

Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии.

2

64

65

66

28

Формула суммы n первых членов геометрической прогрессии

3

67

Контрольная работа № 6

1

Элементы комбинаторики и теории вероятностей

13

68

69

30

Примеры комбинаторных задач

2

70

71

31

Перестановки

2

72

73

32

Размещения

2

74

75

76

33

Сочетания

3

77

34

Относительная частота случайного события

1

78

79

35

Вероятность равновозможных событий

2

80

Контрольная работа № 7

1

Итоговое повторение курса алгебры 7-9 классов

21

81

Числа

1

82

Буквенные выражения

1

83

84

Преобразование выражений

2

85

Проверочная работа №1

1

86

87

Уравнения

2

88

89

Неравенства

2

90

91

Решение задач

2

92

Проверочная работа №2

1

93

94

Последовательности и прогрессии

2

95

96

Функции

2

97

98

99

Решение вариантов экзаменационной работы

3

100

101

Итоговая контрольная работа

2

102

Анализ контрольной работы

2

Уметь (владеть способами познавательной деятельности)

Тема: Свойства функций. Квадратичная функция

- определение функции;

- свойства функций: возрастание, убывание, промежутки знакопостоянства;

- определение квадратного трехчлена;

- корень квадратного трехчлена;

- разложение квадратного трехчлена на множители;

- функция у = ах² + bх + с, её свойства и график;

- степенная функция и ее свойства.

- уметь находить корни квадратного трехчлена;

- уметь раскладывать квадратный трехчлен на множители;

- уметь строить график функции у = ах² + bх + с, указывать координаты вершины параболы, ось симметрии, направление ветвей;

- уметь находить по графику промежутки возрастания и убывания функции, промежутки, в которых функция сохраняет знак;

- уметь находить корни n-й степени.

Тема: Уравнения и неравенства с одной переменной

- определение целого уравнения и его корни;

- степень уравнения;

- определение дробного рационального уравнении и его корни;

- определение неравенства второй степени с одной переменной и методы его решения;

- метод интервалов

- уметь решать целые уравнения с одной переменной с помощью разложения на множители;

- уметь решать целые уравнения с одной переменной с помощью введения вспомогательной переменной;

- решать дробно рациональные уравнения;

- уметь решать неравенства вида ах² + bх + с>0 или ах² + bх + с<0, где а0 с опорой на график квадратичной функции;

- уметь решать неравенства методом интервалов.

Тема: Уравнения и неравенства с двумя переменными

- определение уравнения с двумя переменными и его график;

- определение системы уравнений второй степени;

- решение задач с помощью систем уравнений второй степени;

-определение неравенства с двумя переменными и их системы.

- уметь решать простейшие системы, содержащие уравнение второй степени с двумя переменными способом подстановки;

- уметь решать простейшие системы, содержащие уравнение второй степени с двумя переменными графически;

- решать текстовые задачи с помощью составления систем уравнений второй степени;

- решать графически простейшие неравенства с двумя переменными и их системы.

Тема: Прогрессии

- понятие последовательности;

- определение арифметической прогрессии;

- формулы n-го члена арифметической прогрессии;

- формула суммы первых n членов арифметической прогрессии;

- определение геометрической прогрессии;

- формулы n-го члена геометрической

прогрессии;

- формула суммы первых n членов геометрической прогрессии;

- Бесконечно убывающая геометрическая прогрессия

- уметь находить члены последовательности, заданной формулой;

- уметь находить члены последовательности, заданной реккурентно;

- находить n-й член арифметической прогрессии по формуле;

- находить сумму первых n членов арифметической прогрессии по формуле;

- находить n-й член геометрической прогрессии по формуле;

- находить сумму первых n членов геометрической прогрессии по формуле;

- находить сумму членов бесконечно убывающей геометрической прогрессии

. Тема: Элементы комбинаторики и теории вероятностей

- Комбинаторное правило умножения.

- понятия перестановки, размеще­ния, сочетания.

- понятия относительная частота и вероятность случайного события

- решать простейшие комбинаторные задачи;

- применять комбинаторное правило умножения при решении задач; -

- находить по формуле число перестановок;

- находить по формуле число размещений;

- находить по формуле число

- уметь определять, о каком виде комбинаций идет речь в задаче;

- решать задачи на нахождение вероятности случайного события.

Повторение

Повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры основной общеобразовательной школы.

Организация текущего и промежуточного контроля знаний.

Квадратичная функция.

Урок 10

Контрольная работа № 2 «Квадратичная функция и ее график»

Урок 22

Контрольная работа № 3 «Уравнения и неравенства с одной переменной»

Уравнения и неравенства с одной переменной

Урок 36

Контрольная работа № 4 «Уравнения и неравенства с одной переменной»

Уравнения и неравенства с двумя переменными

Урок 53

Контрольная работа № 5 «Арифметическая прогрессия»

Арифметическая и геометрическая прогрессии

Урок 61

Контрольная работа № 6 «Геометрическая прогрессия»

Урок 67

Контрольная работа № 7 «Элементы комбинаторики и теории вероятностей»

Элементы комбинаторики и теории вероятностей

Урок 80

Итоговая контрольная работа

Повторение

Урок 100, 101

Критерии и нормы оценки знаний, умений и навыков обучающихся по математике.

1. Оценка письменных контрольных работ обучающихся по математике.

Ответ оценивается отметкой «5», если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

• допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

• работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

2.Оценка устных ответов обучающихся по математике

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

• продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

• отвечал самостоятельно, без наводящих вопросов учителя;

• возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

• допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

• неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);

• имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится, если:

• ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.

Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

Грубыми считаются ошибки:

• незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

• незнание наименований единиц измерения;

• неумение выделить в ответе главное;

• неумение применять знания, алгоритмы для решения задач;

• неумение делать выводы и обобщения;

• неумение читать и строить графики;

• неумение пользоваться первоисточниками, учебником и справочниками;

• потеря корня или сохранение постороннего корня;

• отбрасывание без объяснений одного из них;

• равнозначные им ошибки;

• вычислительные ошибки, если они не являются опиской;

• логические ошибки.

К негрубым ошибкам следует отнести:

• неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

• неточность графика;

• нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

• нерациональные методы работы со справочной и другой литературой;

• неумение решать задачи, выполнять задания в общем виде.

Недочетами являются:

• нерациональные приемы вычислений и преобразований;

• небрежное выполнение записей, чертежей, схем, графиков.

Учебно-методические средства обучения.

1. Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Алгебра 9 класс Москва Просвещение 2006, 2009

2. Макарычев Ю.Н., Миндюк Н.Г.под ред. Теляковского С.А.Алгебра: элементы статистики и теории вероятностей: уч. пособие для учащихся 7-9кл. Москва. Просвещение. 2006г.

3. Макарычев Ю.Н., Миндюк Н. Г., Короткова Л. М. Дидактические материалы по алгебре для 9 класса Москва Просвещение 2006

4. Мордкович А. Г. , Тульчинская Е. Е. Алгебра 7-9. Тесты. Москва Мнемозина. 2002

5. Дорофеев Г.В и др. Оценка качества подготовки выпускников основной школы по математике. Москва. Дрофа.2000г.

6. Кузнецова Г.М .Программно-методические материалы. Математика.5-11кл. Сборник нормативных документов. Москва. Дрофа.2001г.

Кузнецова Г.М., Миндюк Н.Г. Программы для общеобразовательных школ, гимназий, лицеев. Математика.5-11кл. Москва. Дрофа.2000г.

Для проведения государственной (итоговой) аттестации по математике

Кочагина М. Н, Кочагин В. В. ГИА 2009. Математика. Сборник заданий. Москва Эксмо 2009

Кузнецова Л.В. Суворова С.Б. Бунимович Е.А. и др. Государственная итоговая аттестация выпускников 9классов в новой форме. Алгебра. 2009. Москва. Интеллект-Центр.2009г.

Кузнецова Л. В, Суворова С. Б, Бунимович Е. А. Алгебра. Сборник заданий к итоговой аттестации в 9 классе. Москва Просвещение 2008

Кузнецова Л. В, Суворова С. Б, Бунимович Е.А. ГИА выпускников 9 классов в новой форме. Алгебра 2010. Москва Интеллект-Центр 2010

Кузнецова Л. В, Суворова С. Б, Бунимович Е.А. ГИА 2010. 9 класс.Тематические тренировочные задания. Москва Эксмо 2010

Лаппо Л. Д, Попов М. А. ГИА. Математика: сборник заданий. Москва "Экзамен"

Лаппо Л. Д, Попов М. А. ГИА. Алгебра Практикум Москва "Экзамен"

1</ Помимо указанных в данном разделе знаний, в требования к уровню подготовки включаются также знания, необходимые для освоения перечисленных ниже умений.