Конспект к уроку Основные способы преобразования графиков11 класс

Муниципальное общеобразовательное учреждение

«Ново-Девяткинская СОШ №1»

«Основные способы преобразования графиков функций»

(для учащихся 11 класса)

Тип урока: комбинированный урок

Автор разработки

Учитель математики

высшей категории

Бабаченко Наталья Алексеевна

2015 год

Тема урока: «Основные способы преобразования графиков функций».

Цель урока - организация продуктивной деятельности школьников, направленной на достижение ими:

1. Предметных результатов:

закрепление умений преобразовывать графики функций элементарными способами - симметрия, сдвиг, сжатие-растяжение; понимание значимости умения построить график для исследования свойств функции; отработка умения оперировать математическими терминами, уверенно их употреблять в письменной и устной работе;

умение читать, различать и строить графики функций и по графику определять свойства функций;

овладение опытом исследовательской деятельности при нахождении нового для учащихся вида преобразования графиков.

2. Метапредметных результатов:

освоение способов деятельности:

познавательной

исследование несложных практических ситуаций, выдвижение предложений, понимание необходимости их проверки на практике;

умение мотивированно отказаться от образца, искать оригинальное решение;

умение классифицировать объекты по определённым признакам;

информационно-коммуникативной

умение вступать в речевое общение, принимать и понимать точку зрения собеседника, признавать право на иное мнение;

умение перефразировать мысль (объяснить «иными» словами);

рефлексивной

поиск и устранение причин возникших трудностей; оценивание своих учебных достижений.

3. Личностных результатов:

стимулировать способность иметь собственное мнение;

умение учиться самостоятельно;

умение хорошо говорить и легко выражать свои мысли;

учиться применять полученные знания и навыки к решению новых проблем;

умение уверенно и легко выполнять математические операции.

</

Используемая литература и оборудование.

Алгебра и начала анализа.10-11 кл.:Учеб.-метод. пособие/ М.И.Башмаков и др. - М.:Дрофа,2001.

Устные занятия по математике в ст. классах/ пособие для учителя, Кононов А.Я. - М.: АО «Столетие»,1997

УМК: Алгебра и начала анализа: учеб. для 11 кл. общеобразоват. учреждений: базовый и профил. уровни /С.М.Никольский и др. - М.:Просвещение,2007.

Пособие для учителя «Рабочие программы В.Зыкина»

Компьютер + интерактивная доска+мультимедиапроектор+МФУ.

Лист самоконтроля.

Ход урока.

1.Организационный момент (1 мин.)

Учитель: Добрый день, ребята! Мне приятно снова видеть Вас! Надеюсь вместе с вами, что скоро наступит «бабье лето», у всех хорошее настроение, и мы готовы приступить к работе. Поприветствуем наших гостей.

Тема нашего урока «Основные способы преобразования графиков».

СЛАЙД 1

Сегодня в течение урока вы будете заполнять лист самоконтроля, в котором будут отражены результаты вашей работы. В конце урока вы подсчитаете количество заработанных вами баллов и выставите себе отметку за урок.

2.Постановка цели. (3 мин.)

СЛАЙД 2

Учитель: Сегодняшний урок мне хочется начать с отрывка из одной известной сказки.

« В нескольких шагах от неё сидел Чеширский Кот.

Скажите, пожалуйста, куда мне отсюда идти?

- Это во многом зависит от того, куда ты хочешь прийти, - ответил Кот.

- Да мне почти все равно, - начала Алиса.

- Тогда все равно, куда идти, - сказал Кот.

- Лишь бы попасть куда-нибудь, - пояснила Алиса.

• Не беспокойся, куда-нибудь ты обязательно попадешь, - сказал Кот, - конечно, если не остановишься на полпути.

Учитель : Ребята, как называется сказка, кто её написал?

Учащиеся: Это отрывок из сказки «Алиса в стране чудес». Её написал Льюис Кэрролл.

Учитель: Так что же хотел сказать Алисе Кот?

Учащиеся: Перед тем, как что-то делать, надо поставить цель.

Учитель: Каждый из вас сегодня поставит перед собой личную цель. Выберите из предложенных и запишите ее на листе самоконтроля. Обратите внимание, что все эти цели важны, но вы должны выбрать одну цель, по которой в конце урока вы сможете судить о пользе вашей деятельности на уроке.

СЛАЙД 3

Представлены цели для выбора:

1. - учиться иметь и высказывать собственное мнение;

2. - развивать умение учиться самостоятельно

3. - узнать что-то новое о графиках; мне это интересно;

4. - узнать что-то новое, потому что мне это пригодится в дальнейшей учебе;

5. - отрабатывать умение выполнять известные мне математические операции.

(учащиеся выбирают одну цель из представленного им списка целей и в лист самоконтроля записывают ее.)

3. Актуализация знаний учащихся. Фронтальный опрос. (4-5 мин.)

Учитель: На дом было задано вспомнить все известные вам способы преобразования графиков функций, воспользовавшись учебником п.1.6. Качество выполнения вами д/з мы сейчас проверим фронтальным опросом.

СЛАЙДЫ 4-6

1. Назовите номера лишних рисунков, на которых изображены графики функций. Почему вы считаете их лишними? Дайте определение функции.

2. Пользуясь графиком, назовите свойства функции по предложенному плану.

Используется демонстрационный материал из «Рабочие программы В.Зыкина» - 10 кл. ДМ -14

(Отметим, что график функции лишь иллюстрирует свойства функции, но не доказывает их. Это одно из элементарных средств исследования функции.)

3. Назовите исходную функцию и способ преобразования, которым получен данный график.

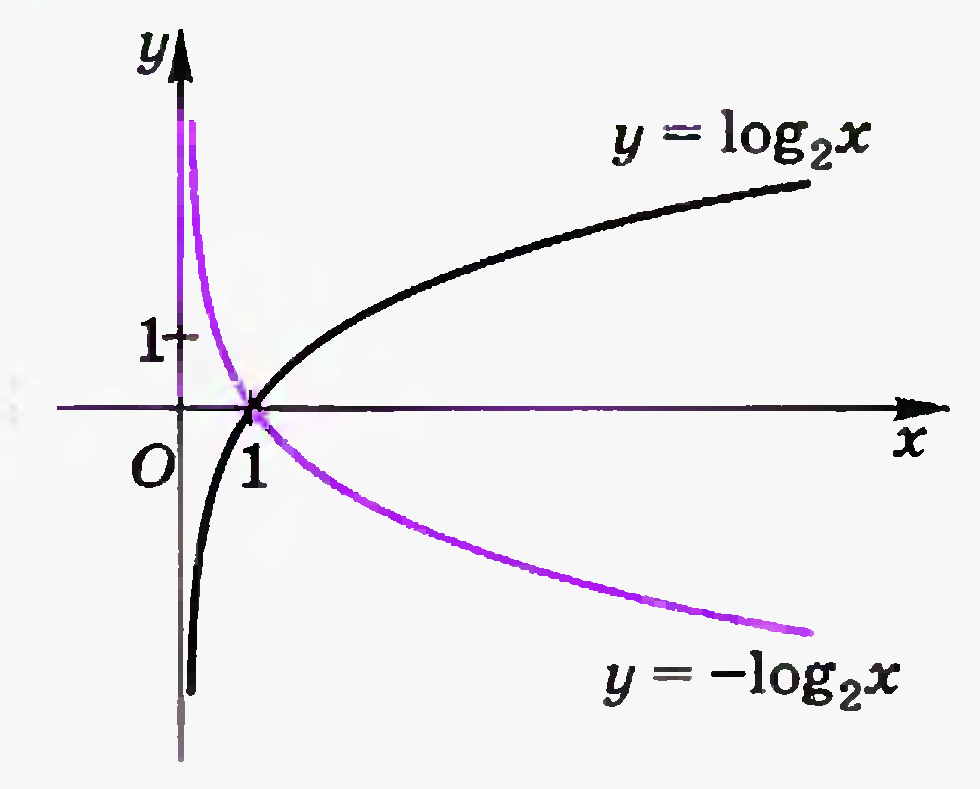
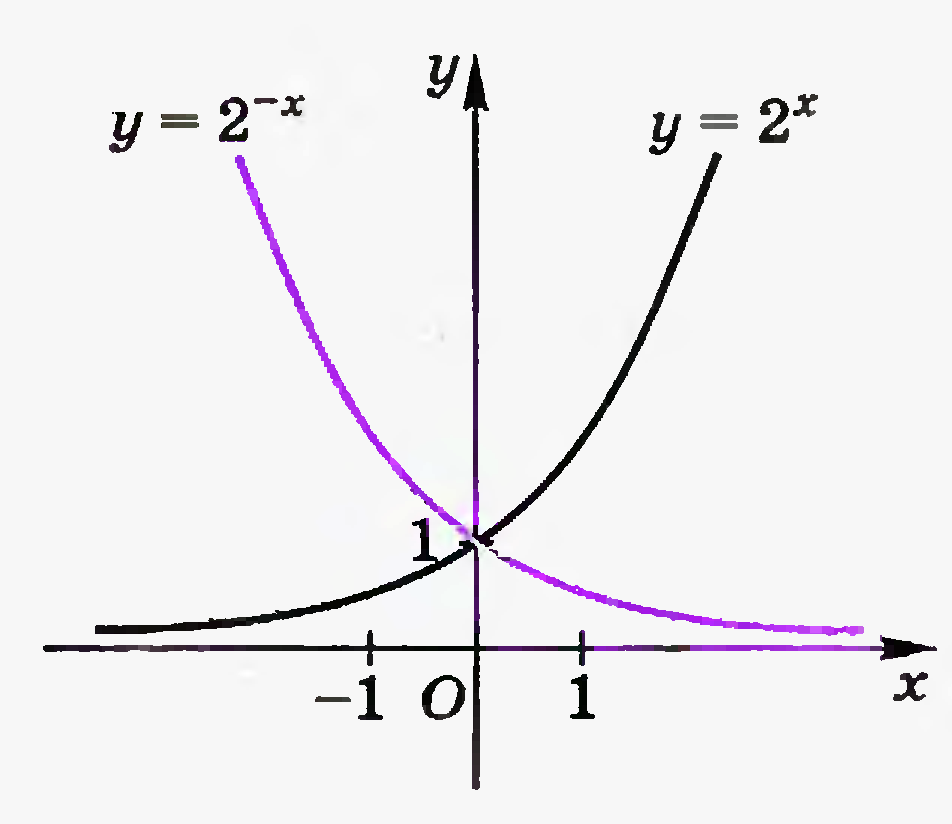
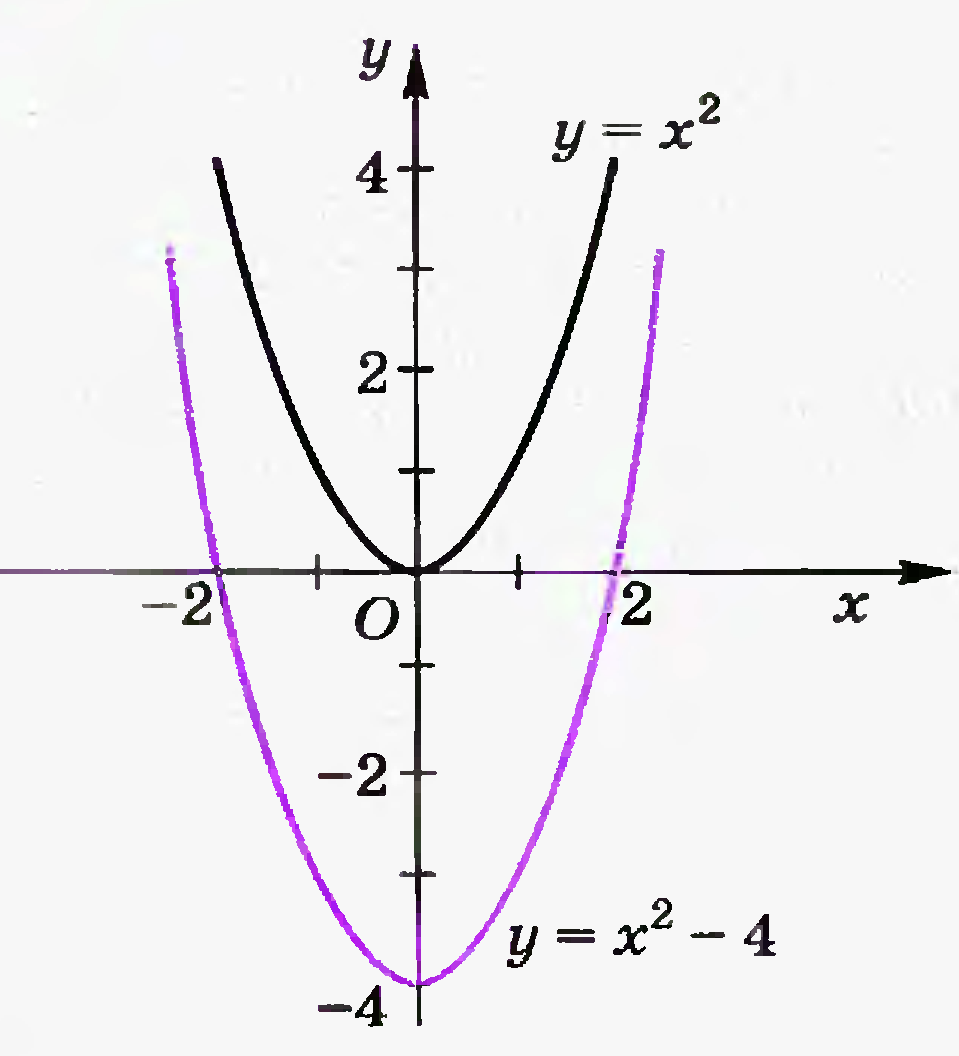
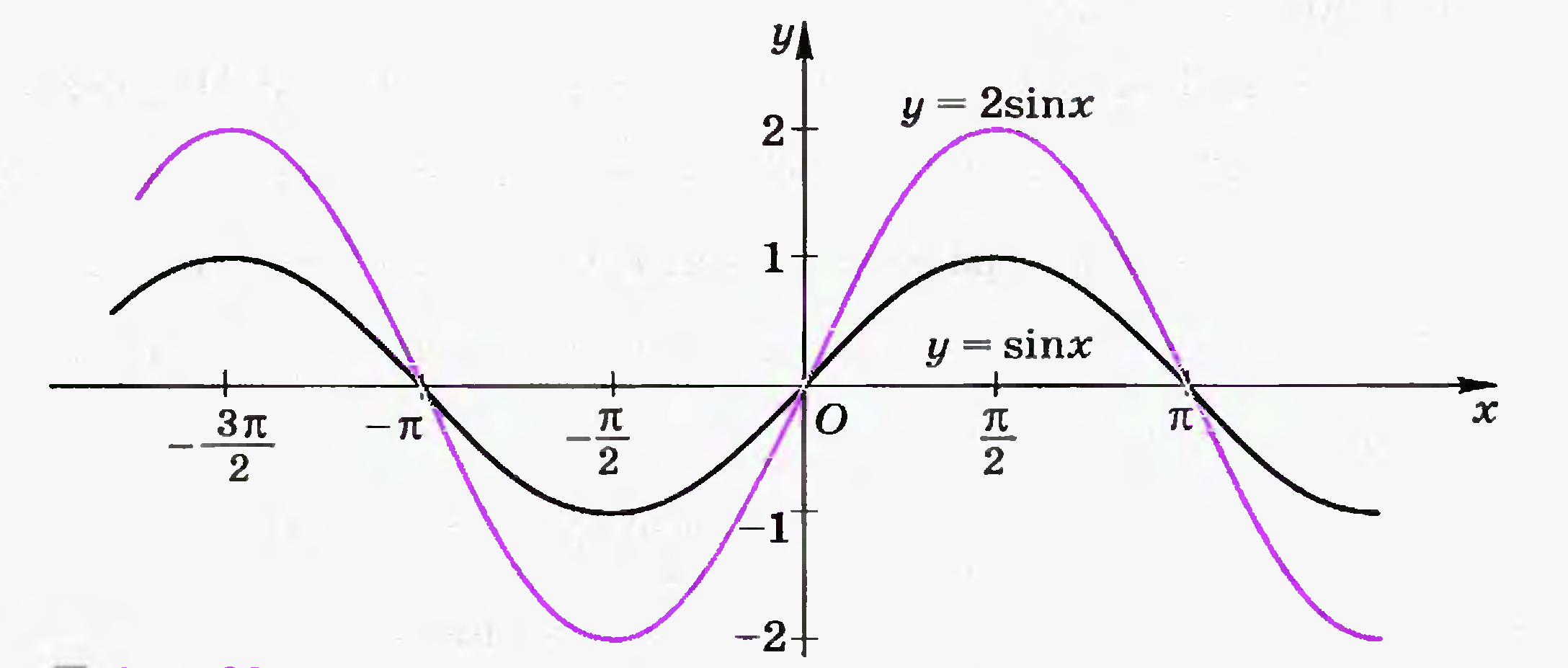
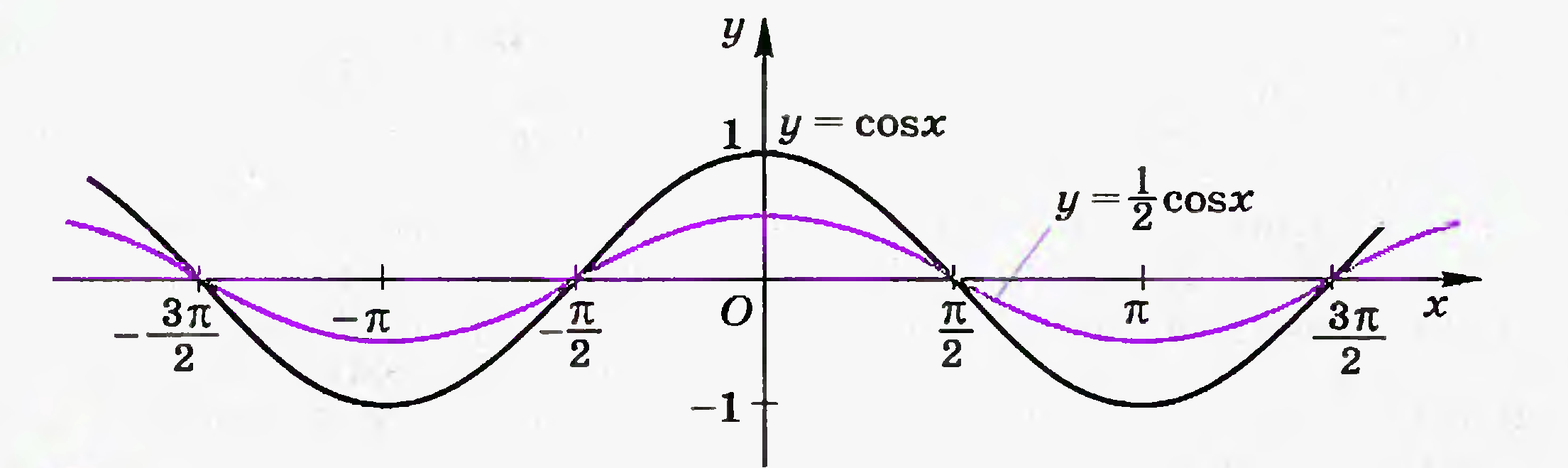
4. Математический диктант.(5-6 мин.)

Учитель: Ответы на математический диктант прошу записать в лист самоконтроля под соответствующим номером. Будьте внимательны. Исправления не допускаются и будут считаться ошибкой.

СЛАЙДЫ 7-8

Какое наименьшее значение принимает функция y=x²-2x+1? (0)

Какой знак имеет функция y=cos2? (отрицательный)

При каких значениях x функция y= x²-5x-6 обращается в нуль? (6; -1)

Найдите область определения функции (x≠πk, kϵZ)

Преобразования графиков. (по уровням)

Вариант А1 Вариант Б1

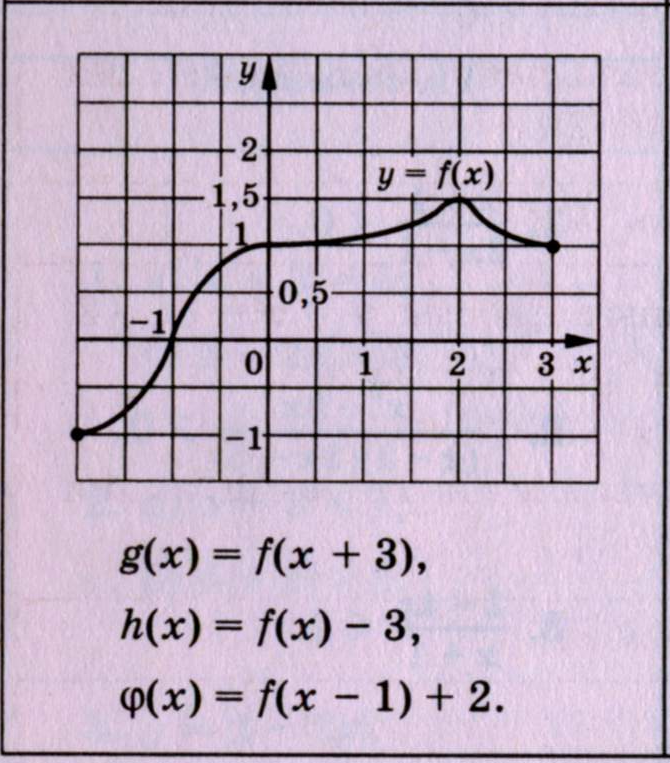
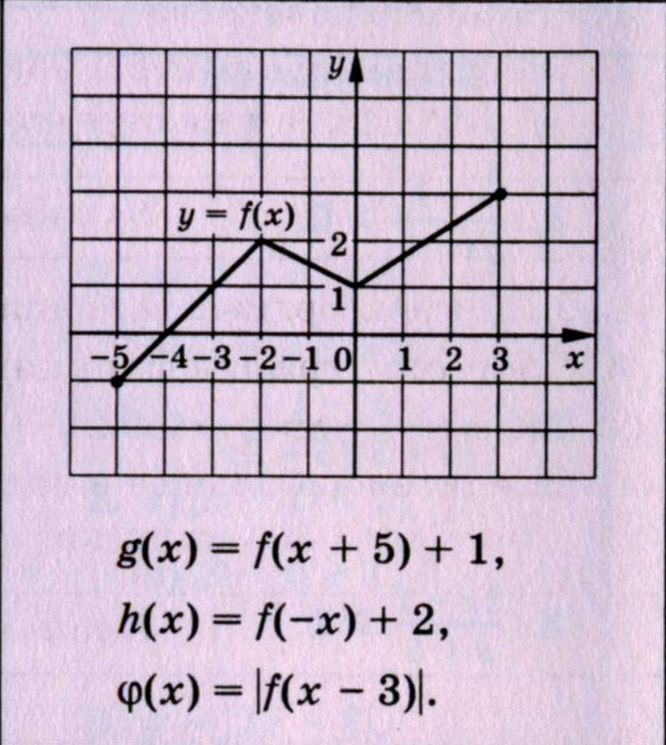
5. Взаимопроверка математического диктанта по предложенным правильным ответам.

СЛАЙДЫ 9-10

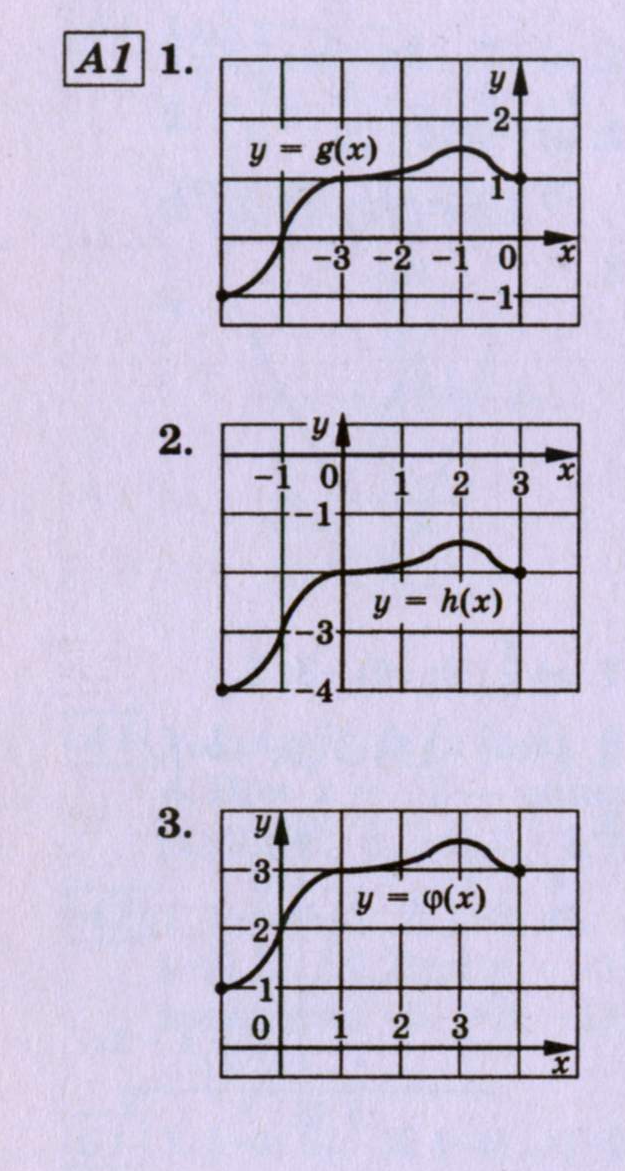
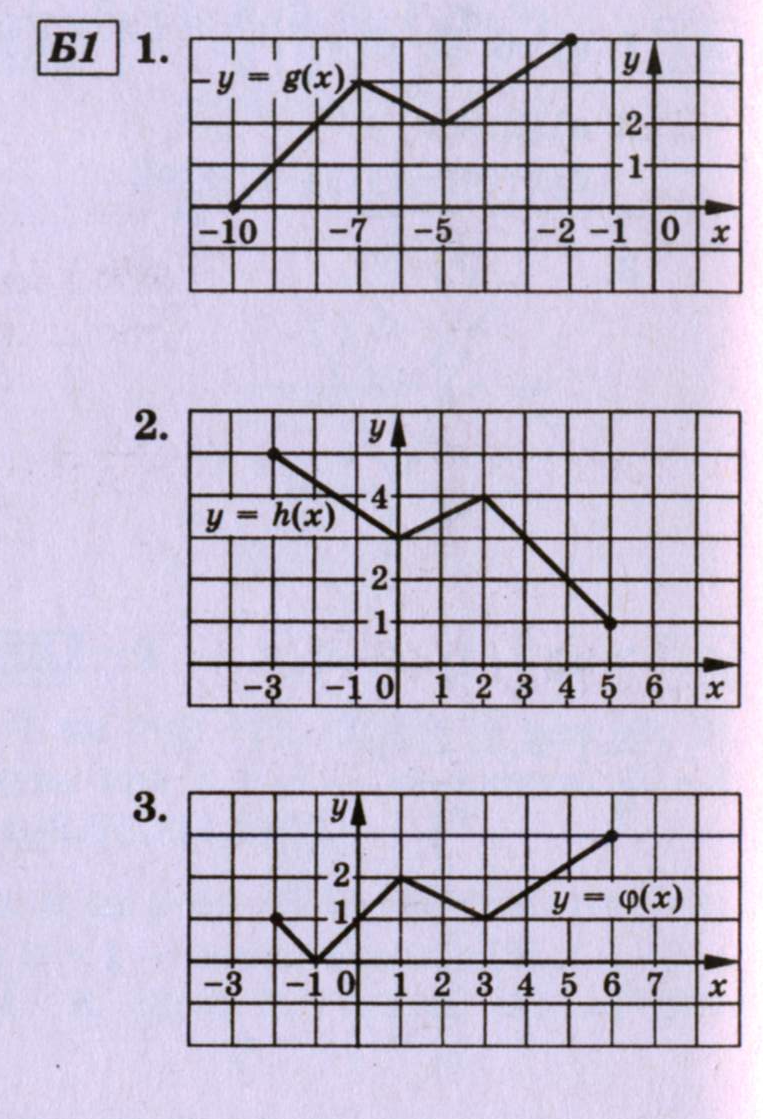
Выставление в лист самоконтроля заработанных баллов.

6. Исследовательская работа по добыванию нового материала.

Учитель: Постройте график функции x=2y. Чем отличается эта функция от ранее изученных? Какая переменная является зависимой? Назовите функцию.

Как можно выполнить построение, используя наши умения и навыки?

Учащиеся: 1) преобразовать формулу в вид

2) строить по точкам, используя таблицу: y - аргумент; x- функция.

Учитель: Предлагаю разделиться и по вариантам проверить оба предложенных способа. 1 вариант преобразует формулу и построит получившуюся функцию.

2 вариант будет строить по таблице. Будьте внимательны при построении точек по координатам.

Учитель: Ребята, посмотрите в тетрадь к соседу. Сделайте вывод о полученном результате.

Учащиеся: Получилась одна и та же линейная функция. Результат не зависит от способа построения.

Учитель: Постройте на этой же координатной плоскости график похожей функции y=2x.

Сравните формулы, чем похожи? Чем отличаются?

Учащиеся: похожи на линейную функцию, отличаются тем, что аргумент и функцию «поменяли местами».

СЛАЙД 11

Учитель: Постройте график функции x=2^y . Теперь 1 вариант строит по этой формуле, используя таблицу значений аргумента и функции, а 2 вариант преобразует формулу в привычный вид, где функция - это y. Какую формулу вы получили?

Учащиеся: y=log₂x

Учитель: Сверьтесь с соседом и убедитесь, что получили одинаковые графики.

Постройте на этой же координатной плоскости график функции y=2^x

Сравните формулы, чем похожи? Чем отличаются?

Учащиеся: похожи на показательную функцию, отличаются тем, что аргумент и функцию «поменяли местами».

СЛАЙД 12

Учитель: Ребята, мы уже встречались с математическими объектами, которые отличались друг от друга порядком расположения «составляющих».

Например, числа 2/9 и 9/2. Что общего у них с парами наших графиков.

Как называются такие числа?

Учащиеся: Числитель и знаменатель меняются местами. Это взаимно обратные числа.

(Хорошо бы еще вспомнить из геометрии свойства и признаки, например, равнобедренного треугольника или параллельных прямых)

Такие функции мы назовем обратными.

7. Закрепление нового материала.

Посмотрите на графики, построенные нами и найдите способ преобразования, которым можно из одной функции получить ей обратную.

СЛАЙД 13

Учитель: Графики обратных функций симметричны относительно прямой y=x

СЛАЙД 14

Учитель: Итак, мы узнали еще один способ преобразования, которым можно получить график неявно заданной функции. Это симметричное отображение относительно прямой y=x.

Давайте потренируемся в узнавании таких функций и попытаемся по графику задать функцию формулой.

СЛАЙД 15

Решение, а) На рисунке 20, а изображена парабола у = ах², проходящая через точку (1; 2). Так как 2 = а • 1² при а = 2, то это парабола у = 2х².

б) На рисунке 20, б изображена парабола у = ах², проходящая через точку (1; -2). Так как - 2 = а • 1² при а = -2, то это парабола у =-2х².

в) На рисунке 20, в изображена парабола х = ay²,

проходящая через точку (2; 1). Так как 2 = а • 1² при а = 2, то это парабола х = 2у².

г) На рисунке 20, г изображена парабола у = ах², проходящая через точку (-2; 1). Так как -2 = а • 1² при а = -2, то это парабола x=-2y²

д) На рисунке 20, д изображена парабола у = а (х - 1)² + 1, так как ее вершина (х₀; у₀) имеет координаты (1; 1). Парабола проходит через точку (0; 3), поэтому из равенства 3 = а (0 - 1)² + 1 следует, что а = 2. Итак, это парабола y=2(х-1)² + 1.

е) На рисунке 20, е изображена парабола у = а (х - 1)² + 2, так как ее вершина (х₀; у₀) имеет координаты (1; 2). Парабола проходит через точку (0; 0), поэтому из равенства 0 = а (0 - 1)² + 2 следует, что а = -2. Итак, это парабола у = -2 (х - 1)² + 2.

8. Закрепление нового материала. Самостоятельная работа.

СЛАЙД 16

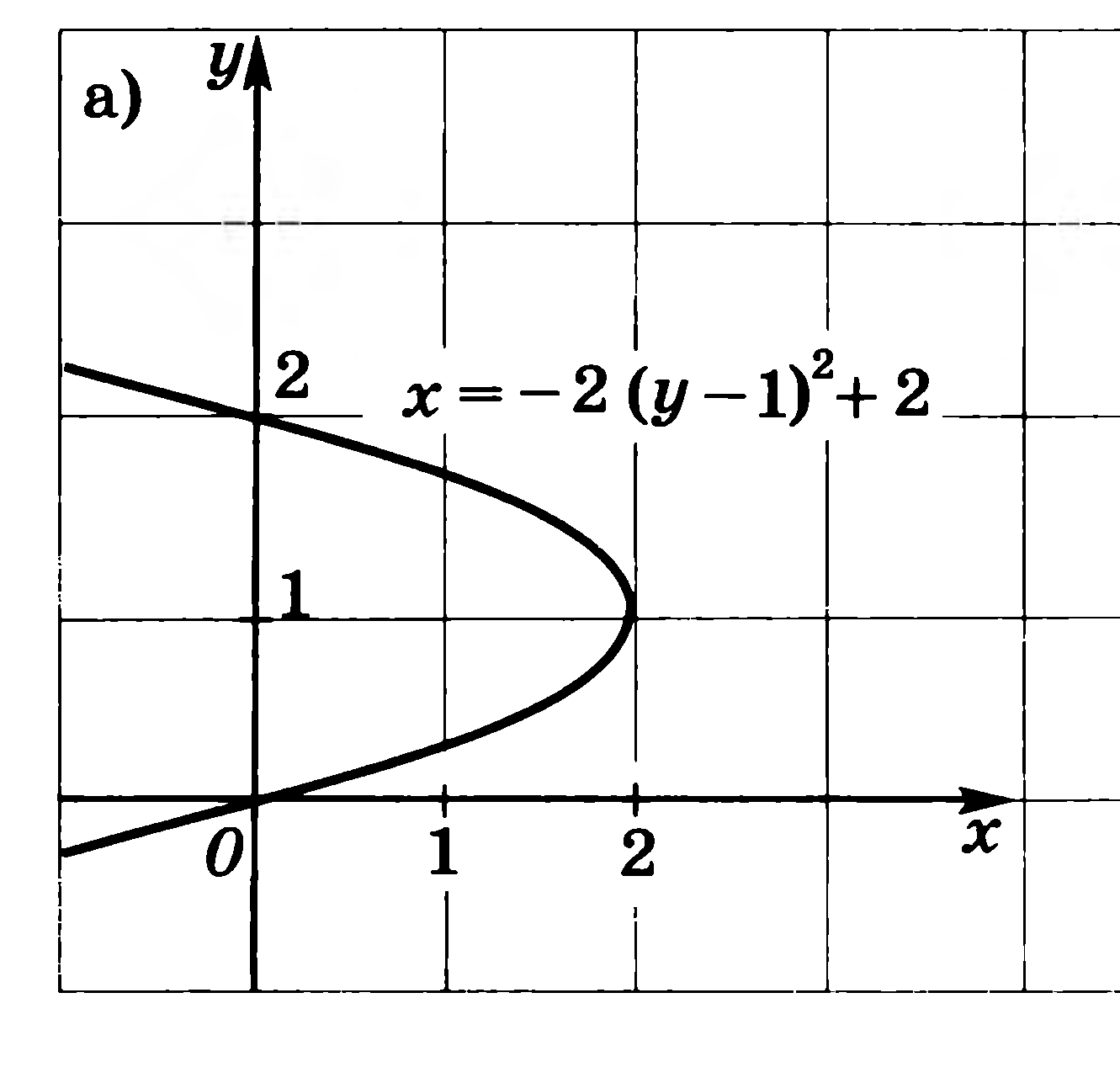
Выполните необходимые преобразования и задайте формулой функцию изображенного на рисунке графика.

Последовательность выполнения:

1) Построить симметрию

2) Задать формулой получившийся график

3) Сделать замену в формуле и получить формулу данной функции

9. Проверка самостоятельной работы.

СЛАЙД 17

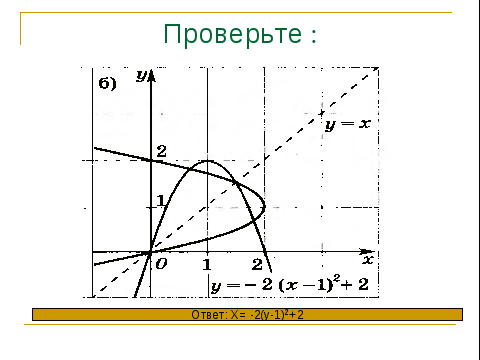
10.Подведение итогов урока.ЭТАП УРОКА

ЗАРАБОТАННЫЕ БАЛЛЫ

БАЛЛ

1. Фронтальная работа

Дополнительный балл

2. Математический диктант

7 6 5 4 3 2 1

3. Исследовательская работа

Дополнительный балл

4. Самостоятельная работа

3 2 1

ИТОГ МОЕЙ РАБОТЫ

10-12 баллов - «5»

7 -9 баллов - «4»

4-6 баллов - «3»

Менее 4 баллов - «2»

БАЛЛЫ

ОТМЕТКА

Сейчас вы оцените свою работу на уроке. Внесите в лист самоконтроля заработанные вами баллы. Подведите итог и выставьте отметку согласно шкале перевода баллов в отметку.

Что нового вы узнали на уроке?

Посмотрите на свою личную цель на листе самоконтроля и скажите, достигли ли вы ее?

11. Домашнее задание.

СЛАЙД 19

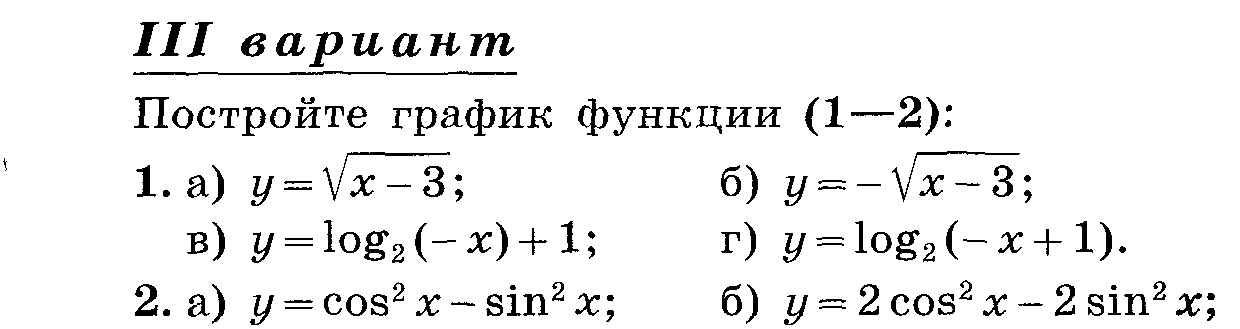
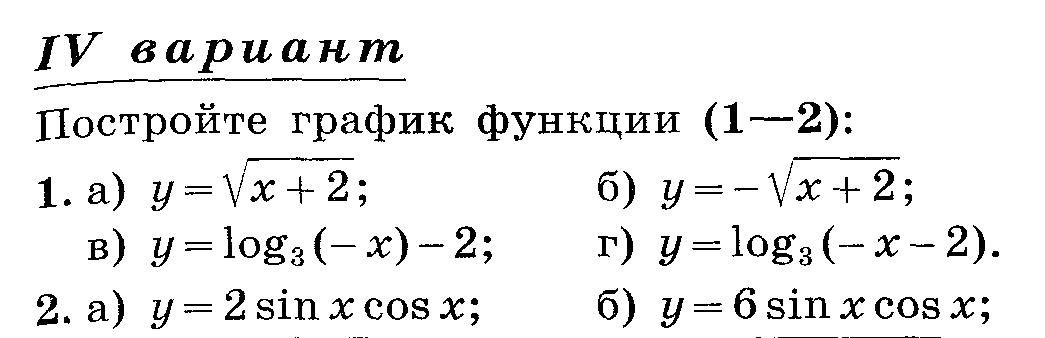
Используйте изученные способы преобразования графиков для построения.

Укажите последовательность преобразований.

Прошу сдать листы самоконтроля.

Урок окончен. До свидания.