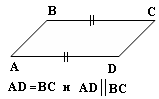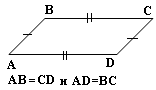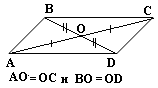- Учителю
- Опорный конспект по теме параллелограмм.
Опорный конспект по теме параллелограмм.
|
Классная работа. Тема «Параллелограмм». Обобщаем все знания о параллелограмме. | |||||
|
| ||||
|
2. Свойства сторон параллелограмма. 1) У параллелограмма противоположные стороны параллельны. 2)У параллелограмма противоположные стороны попарно равны. |
1) то АВIIDС, ADIIBC (по определению) | ||||
|
2 то АВ=DС, AD=BC (по свойству сторон) | |||||
|
3. Свойства углов параллелограмма 1) У параллелограмма противоположные углы попарно равны.
2) Сумма соседних углов параллелограмма равна 1800. |
то ∟А=∟С, ∟D=∟B (по свойству углов) 2) | ||||
|
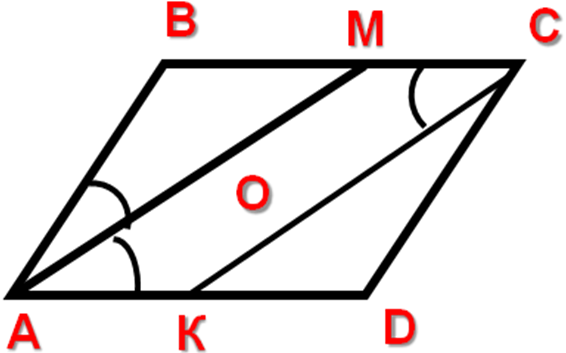
4. Свойства биссектрис параллелограмма 1)Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. 2)Биссектрисы соседних углов параллелограмма перпендикулярны. 3)Биссектрисы противоположных углов параллелограмма параллельны. |
1) 2) |
|
3) |
| |
|
|
|
| |||
|
5. Свойство диагоналей параллелограмма 1)Диагонали параллелограмма точкой пересечения делятся пополам. 2)Диагональ делит параллелограмм на два равных треугольника.
|
1)
2) |
| |||
|
5. Признаки параллелограмма 1 признак Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник - параллелограмм.
2 признак Если в четырёхугольнике противоположные стороны равны, то этот четырёхугольник - параллелограмм.
3 признак Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм. |
1)
|
| |||
|
2)
|
| ||||
|
3) |
| ||||
Если АВСD -
параллелограмм,
Если АВСD -
параллелограмм,
Тема «Параллелограмм». Лист опроса. Ф. И.
1. Определение.
2. Свойства сторон параллелограмма.
1)
2)
1)
2)
3. Свойства углов параллелограмма
1)
2)
1)
2)
4. Свойства биссектрис параллелограмма
1)
2)
3)
1)
2)
3)
4. Свойство диагоналей параллелограмма
1)
2)
1)
2)
5. Признаки параллелограмма
1 признак
2 признак
3 признак
1)
2)
3)