- Учителю
- Сборник задач по теме Решение уравнений в 8 классе
Сборник задач по теме Решение уравнений в 8 классе
Мугудайская средняя общеобразовательная школа им. Д.Д.Красильникова
СБОРНИК ЗАДАЧ ПО ТЕМЕ «РЕШЕНИЕ УРАВНЕНИЙ» В 8 КЛАССЕ
2011г.
СОДЕРЖАНИЕ
Пояснительная записка…………………………………………………………...
Календарно-тематическое планирование………………………………………..3
-
КВАДРАТНЫЕ УРАВНЕНИЯ…………………………………4
-
Задачи для предварительного контроля………………….…….4
-
Задачи для текущего контроля………………………………….9
-
Задачи для итогового контроля..……………………………….15
-
ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ………………..
-
Задачи для предварительного контроля………………….…….4
-
Задачи для текущего контроля………………………………….9
-
Задачи для итогового контроля..…………………………. Приложение………………………………………………………………28
Ответы
Пояснительная записка
Изучение материала линии уравнений имеет основной учебной целью овладение учащимися на том или ином уровне приемами решения (алгебраического и графического) уравнений как математического аппарата решения задач из математики, смежных областей знаний и практики. Содержание этого материала также позволяет продолжить развитие у учащихся познавательных процессов, речи и умения учиться, алгоритмического и обобщенного мышления, элементов творческой деятельности при решении всех основных типов задач алгебраическим методом.
Данный сборник задач ставит своей целью помочь учителям средних классов в подборе задач для контроля знаний учащихся 8 класса по темам «Квадратные уравнения» и «Дробно-рациональные уравнения». По каждой теме приводятся задачи к 3 видам контроля: предварительный, текущий и итоговый.
В данном сборнике собраны задачи по теме «Решение уравнений» путем соотнесения видов контроля знаний учащихся по математике с требованиями к знаниям и умениям учащихся. Сборник может быть использован в виде методического пособия при изучении тем «Квадратные уравнения» и «Дробно-рациональные уравнения».
Общее количество заданий 625, контрольных работ 2, самостоятельных работ 10, которые входят в приложении и ответы к задачам.
Квадратные уравнения.
Предварительный контроль знаний.
-
Найдите корень уравнения разными способами:
-
5х=-60
-
-10х=8
-
7х=9
-
6х=-50
-
-9х=-3
-
0,5х=1,2
-
0,7х=0
-
-1,5=6
-
42х=13
-
5х-150=0
-
48-3х=0
-
-1,5-9=0
-
12х-1=35
-
-х+4=0
-
1,3х=54+х
-
7=6 - 02,х
-
0,15х+6=51
-
-0,7+2=65
-
(у+4)-(у-1)=6у
-
3р-1- (р+3)=1
-
6х-(7х-12)=101
-
20х=19-(3+12х)
-
(13х-15)-(9+6х)=-3
-
12-(4х-18)=(36+4х)+(18-6х)
-
1,6х-(х-2,8)=(0,2+1,5)-0,7
-
(0,5х+1,2)-(3,6-4,5х)=(4,8-0,3х)+(10,5х+0,6)
-
Решите линейное уравнения:
-
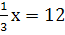
-
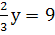
-
-4х=

-
5у=-

-
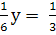
-
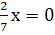
-
3х=75
-
9х=0
-
5-2(х-6)=4
-
х-0,3(1-2х)=2,9
-
1-2х=15
-
(х-0,3)-(2х+0,7)=3
-
2х+9=13-х
-
14-у=19 -11у
-
0,5а+11=4-3а
-
1,2к+1=1-к
-
1,7-0,3р=2+1,7р
-
0,8х+14=2-1,6х
-
х=-х
-
5у=6у
-
5х+(3х-3)=6х+11
-
3а-(10+5а)=54
-
(х-7)-(2х+9)=-13
-
0,6+(0,5у-1)=у+0,5
-
2х+5=2(х+1)+11
-
5(2у-4)=2(5у-10)
-
3у-(у-19)=2у
-
6х=1-(4-6х)
-
15(х+2)-30=12х
-
6(1+5х)=5(1+6х)
-
3у+(у-2)=2(2у-1)
-
6у-(у-1)=4+5у
-
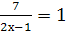
-
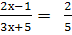
-
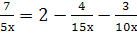
-
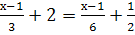
-
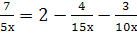
-
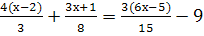
-
Найдите значение арифметического квадратного корня:
4. Вычислите:
-
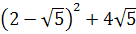
-
(5 +
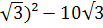
-
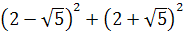
-
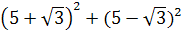
-
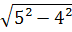
-
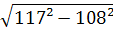
-
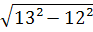
-
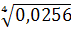
-
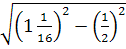
-
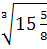
-
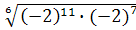
-
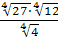
-
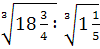
-
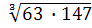
-
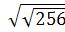
-
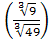
5. Найдите значение выражения:
-
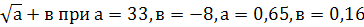
-
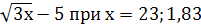
-
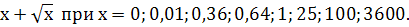
-
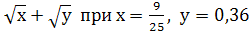
-
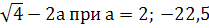
-
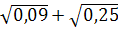
-
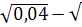 0,01
0,01
-
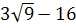
-
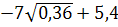
-
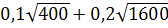
-
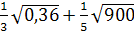
-
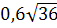
-
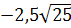
-
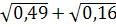
-
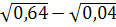
-
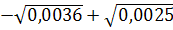
-
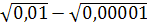
-
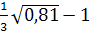
-
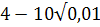
-
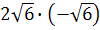
-
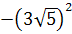
-
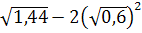
-
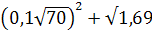
6. Найдите значение переменной х, при котором:
-
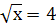
-
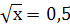
-
2
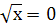
-
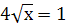
-
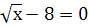
-
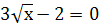
7. При каком значении переменной х, верно равенство:
8. Покажите пример уравнений:
-
полных
-
неполных
-
приведенных
9. При каком значении переменной:
-
Значение выражения 8в - 27 равно -11
-
Значение выражения 3-5с на 1 меньше значения выражения 1-с
-
Значения выражений 2m-13 и m+3 равны
-
Значение выражения 2х+1 на 20 больше значения выражения 8х+5
-
Значение х в 3 раза меньше значения выражения 45-10х
-
Значение выражения 9-у в 2 раза больше значения у.
10. При каком значении у:
-
Значения выражений 5у+3 и 36-у равны
-
Значение выражения 7у-2 больше значения выражения 2у на 10
-
Значение выражения 1,7у+37 меньше значения выражения 9,3у-25 на 14.
Текущий контроль знаний.
-
Выберите из данных примеров квадратные уравнения:
-
3,7х²-5х+1=0
-
48х²-х³-9=0
-
2,1х²+2х -
 =0
=0
-
1-12х=0
-
7х²-13=0
-
-х²=0
-
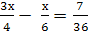
-
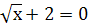
-
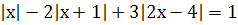
-
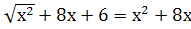
-
5-2(х-6)=4
-
х³
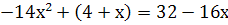
-
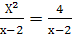
-
45х-18=5(2-5х)²
-
-6(2х+9)=102
2.Напишите коэффициенты квадратных уравнений:
-
х²+3х-10=0
-
-х²-8х+1=0
-
х²+5х=0
-
6х²-30=0
-
9х²=0
-
7х²-8х-2=0
-
8х-х²=0
-
х²-11=0
-
3х²-х=0
-
15х-4х²+7=0
-
-х²+х-5=0
-
9-х²+х=0
-
4х²-7х+3=0
-
х²+2х+
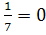
-
3х-4=х²
-
4+х+х²=0
-
6х²-5х=2
-
15-3х²=5х
-
4х²+5х+7=0
-
8х²-3х+4=0
-
-3х²+х-5=0
-
х²-4=0
-
3х²-х=0
-
13х²=0
-
4х²-5+х=0
-
5-6х+х²=0
-
4-2х²-х=0
-
2х²+3х+1=0
-
5х²-9х+4=0
-
х²+5х-6=0
3. Вычислите дискриминант квадратного уравнения:
-
2х²+3х+1=0
-
2х²+х+2=0
-
9х² +6х+1=0
-
х²+5х-6=0
-
3х²-7х+4=0
-
5х²-8х+3=0
-
3х²-13х+14=0
-
2у²-9у+10=0
-
5у²-6у+1=0
-
4х²+х-33=0
-
у²-10у-24=0
-
р²+р-90=0
-
8х²-14х+5=0
-
12х²+16х-3=0
-
4х²+4х+1=0
-
х²-8х-84=0
-
х²+6х-19=0
-
5х²+26х-24=0
-
х²-34х+289=0
-
3х²+32х+80=0
-
Решить уравнения:
-
(х-5)²=16
-
(х-1)²=1
-
3х²-7х=0
-
(х+2)²=9
-
х²-5х=0
-
4х²-9=0
-
х²-25=0
-
(х+2)²=0
-
-3х²+15=0
-
4х²+3=0
-
-х²+6х+1,4=0
-
8х²-7х=0
-
х²-
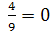
-
4х²+9х=0
-
3х²-4х=0
-
-5х²+6х=0
-
10х²+7х=0
-
4а²
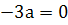
-
6z²-z=0
-
2y+y²=0
-
2x²+3x=0
-
3x²-2=0
-
5u²-4u=0
-
7a-14a²=0
-
1-4y²=0
-
2x²-6=0
-
3x²+32x+80=0
-
2x²-5x-3=0
-
3x²-8x+5=0
-
5x²+9x+4=0
-
36y²-12y+1=0
-
3t²-3t+1=0
-
x²+9x-22=0
-
4x²-3x+7=2x²+x+7
-
-5y²+8y+8=8y+3
-
10-3x²=x²+10-x
-
1-2y+3y²=y²-2y+1
-
x²-5=(x+5)(2x-1)
-
2x-(x+1)²=3x²-6
-
6a²-(a+2)²=-4(a-4)
-
(5y+2)(y-3)=-13(2+y)
-
4x²-7x+3=0
-
4x²+12x+9=0
-
x²+4x+7=0
-
-2x²+12=0
-
3x²+7x=0
-
x²+6x+8=0
-
7x²-2x-329=0
-
5x²-8x+3=0
-
2x²-3x-2=0
-
3x²-13x+14=0
-
y²-10y-24=0
-
5x²=6x-1,75
-
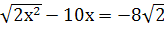
-
25y²+1=10y
-
r²-28r=r-100
-
m²+5m+4=-6-2m
-
(x-1)(x-2)-(x-2)(x-3)=2(x-2)(x-4)
-
11x²+7x -
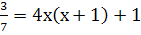
-
5x²-4x=0
-
1-4x²=0
-
2+3x²=0
-
4a²+3a=0
-
2y²-6=0
-
(x+3)(x-4)=-12
-
(3y-1)²-1=0
-
(a-1)(a+1)=2(a²-3)
-
x²-5=(x+5)(2x-1)
-
(2y+3)(3y+1)=11y+30
-
7х²-6х-1=0
-
12х²+7х+1=0
-
х²-12х+36=0
-
7х²-25х+23=0
-
9х²-14х+5=0
-
2х²+3х+1=0
-
2х²+х+2=0
-
9х²+6х+1=0
-
х²+5х-6=0
-
3х²-7х+4=0
-
5х²-8х+3=0
-
3х²-13х+14=0
-
2у²-9у+10=0
-
5у²-6у+1=0
-
4х²+х-33=0
-
у²-10у-24=0
-
р²+р-90=0
-
14х²-5х-1=0
-
-у²+3у+5=0
-
2х²+х+67=0
-
1-18р+81р²=0
-
-11у+у²-152=0
-
18+3х²-х=0
-
3х
 -14х+16=0
-14х+16=0
-
5х²-16х+3=0
-
х²+2х-80=0
-
х²-22х-23=0
-
4х²-36х+77=0
-
15к²-22к-37=0
-
7z²-20z+14=0
-
y²-10y-25=0
-
8x²-14x+5=0
-
12x²+16x-3=0
-
4x²+4x+1=0
-
x²-8x-84=0
-
x²+6x-19=0
-
5x²+26x-24=0
-
x²-34x+289=0
-
100x²-160x+63=0
-
5x²=9x+2
-
-x²=5x-14
-
6x+9=x²
-
z-5=z²-25=0
-
y²=52y-576
-
15y²-30=22y+7
-
25p²=10p-1
-
299x²+100x=500-101x²
-
25=26x-x²
-
3x²=10-29x
-
y²=4y+96
-
3p²+3=10p
-
x²-20x=20x+100
-
25x²-13x=10x²-7
-
(x+4)²=3x+40
-
(2x-3)²=11x-19
-
(x+1)²=7918-2x
-
(x+2)²=3131-2x
-
0,7x²=1,3x+2
-
7=0,4y+0,2y²
-
x²-1,6x-0,36=0
-
z²-2z+2,91=0
-
0,2y²-10y+125=0
-
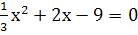
-
x²-5x+6=0
-
y²-12y+32=0
-
Найдите корни уравнения:
-
4x²-9=0
-
-x²+3=0
-
-0.1x²+10=0
-
y²-
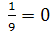
-
6v²+24=0
-
3m²-1=0
-
(x+1)²=(2x-1)²
-
(x-2)²+48=(2-3x)²
-
5x²-x-1=0
-
2x²+7x+4=0
-
3(y²-2)-y=0
-
y²+8(y-1)=3
-
x²-8x+9=0
-
2y²-8y+5=0
-
(x+3)(x-4)=-12
-
1
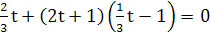
-
3x(2x+3)=2x(x+4,5)+2
-
(x-1)(x+2)=2(x²-3)
-
5x²-11x+2=0
-
2p²+7p-30=0
-
9y²-30y+25=0
-
35x²+2x-1=0
-
2y²-y-5=0
-
16x²-8x+1=0
-
(2x-3)(5x+1)=2x+
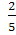
-
(3x-1)(x+3)=(1+6x)
-
(x-1)(x+1)=2(5x-10
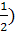
-
-x(x+7)=(x-2)(x+2)
-
3(x+4)²=10x+32
-
15x²+17=15(x+1)²
-
Решите уравнение и укажите приближенные значения корней с точностью до 0,1:
-
2х²-17=0
-
3к²-7,2=0
-
-р²+12,6=0
-
Какое из данных неполных квадратных уравнений не имеет корней:
-
х²-19=0
-
х²+19=0
-
х²-19х=0
-
х²+19х=0
-
Приведите уравнение к виду ах²+вх+с=0:
-
4х²-2х+5=7+2х
-
7х²-6х-3=х²+5х+1
-
(х-3)(2х+4)=-10
-
(8х-1)(4х+2)=(7х+4)(3х-8)
-
(х+12)(3х-5)=(6х-4)(х+7)
-
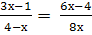
-
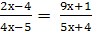
-
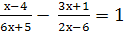
-
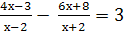
-
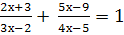
-
В уравнении…
-
х²+рх+18=0 один из корней равен 3. Найти другой корень и коэффициент р.
-
х²-7х+q=0 один из корней равен 9. Найти другой корень и коэффициенты q.
-
Один из корней уравнения…
-
2х²+вх-18=0 равен 2. Найти другой корень и коэффициент в.
-
3х²+14х+с=0 равен -4. Найти другой корень и коэффициент с.
-
Разность корней уравнения…
-
х²+13х+р=0 равна 5. Найти коэффициент р.
-
х²-14х+р=0 равна 4. Найти коэффициент р.
Итоговый контроль знаний.
Контрольная работа.
Вариант 1.
-
Имеет ли корни уравнение:
-
4х²-х+1=0
-
х²-10х+25=0
-
Решите уравнение:
-
х²-5х=0
-
х²+7х+12=0
-
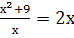
-
Найдите значение х, при которых равны значения выражений (х²+1)²-15 и 2х²+2.
-
Один из корней уравнения х²+
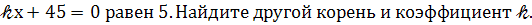
-
Площадь квадрата на 8 см² меньше площади прямоугольника. Сторона квадрата в три раза меньше одной стороны прямоугольника и на 2 см больше второй его стороны. Найдите длину стороны квадрата.
Вариант 2.
-
Имеет ли корни уравнение:
-
х²+5х+3=0
-
3х²-2х+5=0
-
Решите уравнение:
-
2х²+3х=0
-
х²-4х-5=0
-
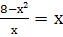
-
Найдите значение х, при которых равны значения выражений (х²-1)²+6 и 16-2х².
-
Один из корней уравнения х²-26
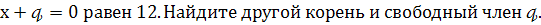
-
Периметр прямоугольника равен 32 см, а его площадь равна 60 см² . Найти длину меньшей стороны прямоугольника.
Вариант 3.
-
Имеет ли корни уравнение:
-
х²-2х+2=0
-
4х²-4х+1=0
-
Решите уравнение:
-
3х-х²=0
-
х²+5х+6=0
-
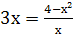
-
Найдите значение х, при которых равны значения выражений (х²-2)²+3 и 11-х².
-
Один из корней уравнения х²+
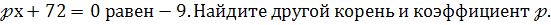
-
Площадь прямоугольника равен 21 см² больше площади квадрата. Одна сторона прямоугольника в 2 раза больше стороны квадрата, а вторая на 1 см меньше первой. Найдите длину стороны квадрата.
Вариант 4.
-
Имеет ли корни уравнение:
-
2х²+5х+3=0
-
х²-3х+4=0
-
Решите уравнение:
-
2х²+5х=0
-
х²-8х+7=0
-
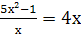
-
Найдите значение х, при которых равны значения выражений 3х²+9 и (х²+3)²-4.
-
Один из корней уравнения х²+11
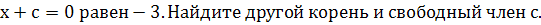
-
Периметр прямоугольника равен 28 см, а его площадь равна 48 см² . Найти длину большей стороны прямоугольника.
Дробно рациональные уравнения.
Предварительный контроль знаний.
-
Сократите дробь:
-
Найти наименьший общий знаменатель для дробей:
-
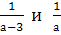
-
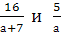
-
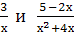
-
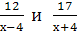
-
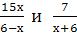
-
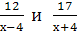
-
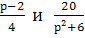
-
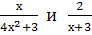
-
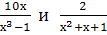
-
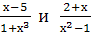
-
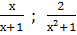 и
и
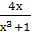
-
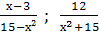 и
и
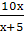
-
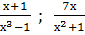 и
и
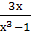
-
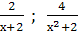 и
и
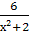
-
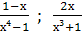 и
и
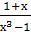
-
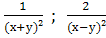 и
и
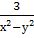
-
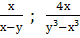 и
и
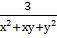
-
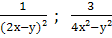 и
и
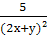
-
Выполните действия:
-
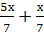
-
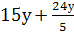
-
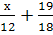
-
8z+8
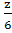
-
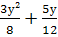
-
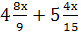
-
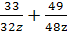
-
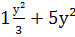
-
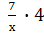
-
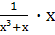
-
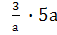
-
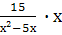
-
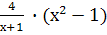
-
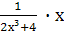
-
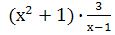
-
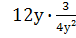
-
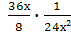
-
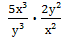
-
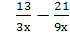
-
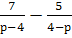
-
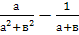
-
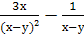
-
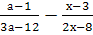
-

-
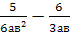
-
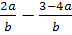
-
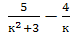
-
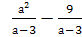
-
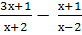
-
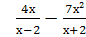
-
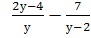
-
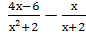
-
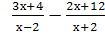
-
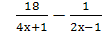
-
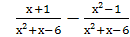
-
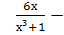
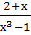
-
Представьте в виде дроби:
-
Упростите выражение:
-
Найдите область допустимых значений уравнений:
-
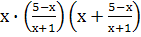 =6
=6
-
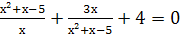
-
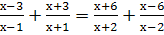
-
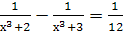
-
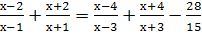
-
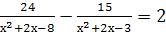
-
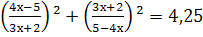
-
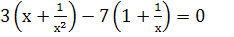
-
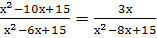
-
х² - 7х + 14 -
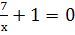
Текущий контроль знаний.
-
Решить уравнение:
-
Найти корни уравнения:
-
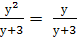
-
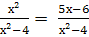
-
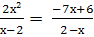
-
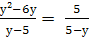
-
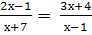
-
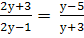
-
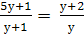
-
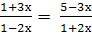
-
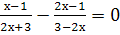
-
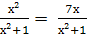
-
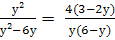
-
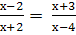
-
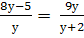
-
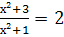
-
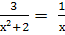
-
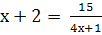
-
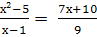
-
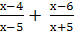 =2
=2
-
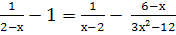
-
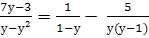
-
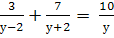
-
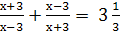
-
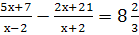
-
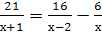
-
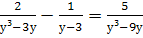
-
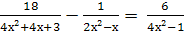
-
При каком значении х:
-
значение функции у =
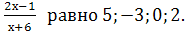
-
значение функции у =
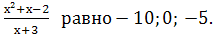
4. Найдите значение переменной у, при котором:
-
Сумма дробей
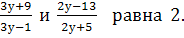
-
Разность дробей
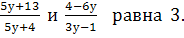
-
Сумма дробей
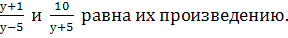
-
Разность дробей
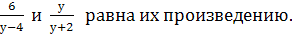
5. Приведите к наименьшему общему знаменателю:
Итоговый контроль знаний.
Контрольная работа №2.
Вариант 1.
-
Найти корни уравнения:
2. Найти наименьший общий знаменатель дробей:
3. Решить уравнение:
Вариант 2.
-
Найти корни уравнения:
2. Найти наименьший общий знаменатель дробей:
3. Решить уравнение:
ПРИЛОЖЕНИЕ
Самостоятельная работа №1.
Вариант 1.
-
Приведите уравнение (2х-4)(х+1)=3х+2 к виду ах²+вх+с=0 и выпишите его коэффициенты.
-
Составьте квадратное уравнение, зная его коэффициенты а = 2, в =
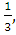 с =
-
с =
-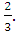
-
Докажите, что число
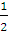 является
корнем этого уравнения.
является
корнем этого уравнения.
-
Решите неполное квадратное уравнение:
-
х²- 7х=0
-
х²-121=0
-
3х²=0
Вариант 2.
-
Приведите уравнение (3-2х)(х-1)=х-2 к виду ах²+вх+с=0 и выпишите его коэффициенты.
-
Составьте квадратное уравнение, зная его коэффициенты а =
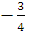 , в
=
, в
=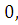 с
= 3
с
= 3
-
Докажите, что число
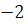 является
корнем этого уравнения.
является
корнем этого уравнения.
-
Решите неполное квадратное уравнение:
х²- 196=0
2х²- 3х=0
х²+1=0
Вариант 3.
-
Приведите уравнение (5х+3)(4-х)=х²- 7 к виду ах²+вх+с=0 и выпишите его коэффициенты.
-
Составьте квадратное уравнение, зная его коэффициенты а =
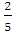 , в
=
, в
=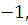 с
= 0
с
= 0
-
Докажите, что число
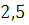 является
корнем этого уравнения.
является
корнем этого уравнения.
-
Решите неполное квадратное уравнение:
-0,5х²=0
2х²+ 7=0
3х²+х=0
Вариант 4.
-
Приведите уравнение (4х+5)(3-х)=х²-2х к виду ах²+вх+с=0 и выпишите его коэффициенты.
-
Составьте квадратное уравнение, зная его коэффициенты а =
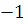 , в
=
, в
=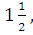 с
= 2,5
с
= 2,5
-
Докажите, что число
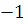 является
корнем этого уравнения.
является
корнем этого уравнения.
-
Решите неполное квадратное уравнение:
х²- 12=0
5х²+2х=0
![]() х²=0
х²=0
Самостоятельная работа №2.
Вариант 1.
-
Решите уравнение:
-
х²+5х-24=0
-
25х²-10х+1=0
-
-4х²+19х-12=0
-
3х²-5х+3=0
-
При каких значениях параметра р уравнение 2х²+рх+6=0 имеет один корень?
Вариант 2.
-
Решите уравнение:
-
х²+х-42=0
-
7х²+х+1=0
-
-5х²+23х+10=0
-
16х+8х+1=0
-
При каких значениях параметра р уравнение 5х²+рх+4=0 имеет один корень?
Вариант 3.
-
Решите уравнение:
-
х²+2х-63=0
-
25х²-30х+9=0
-
-7х²-46х+21=0
-
2х²+3х+5=0
-
При каких значениях параметра р уравнение 3х²+рх-р=0 имеет один корень?
Вариант 4.
-
Решите уравнение:
-
х²+3х-28=0
-
3х²-х+1=0
-
-6х²+37х-6=0
-
9х²+24х+16=0
-
При каких значениях параметра р уравнение -4х²+рх-р=0 имеет один корень?
Самостоятельная работа №3.
Вариант 1.
-
Решите задачу. Один катет прямоугольного треугольника на 7 дм больше другого. Найти длину каждого катета и площадь треугольника, если длина гипотенузы равна 17 дм.
-
Решите уравнение:
![]()
Вариант 2.
-
Решите задачу. Один катет прямоугольного треугольника на 14 см меньше другого. Найти длины сторон прямоугольного треугольника, если его площадь равна 120 см².
-
Решите уравнение:
![]()
Вариант 3.
-
Решите задачу. Диагональ прямоугольника на 1 см больше одной стороны и на 8 см больше другой стороны прямоугольника. Найти стороны прямоугольника и его площадь.
-
Решите уравнение:
![]()
Вариант 4.
-
Решите задачу. Гипотенуза прямоугольного треугольника на 8 дм больше одного катета и на 9 дм больше другого. Найти стороны этого треугольника.
-
Решите уравнение:
![]()
Самостоятельная работа №4.
Вариант 1.
-
Решите уравнение:
-
Решите уравнение методом введения новой переменной:
-
4х⁴-17х²+4=0
-
(х²-2х)²+(х²-2х)=12
Вариант 2.
-
Решите уравнение:
-
Решите уравнение методом введения новой переменной:
-
9х⁴-13х²+4=0
-
(х²-8)²+3(х²-8)=4
Вариант 3.
-
Решите уравнение:
-
Решите уравнение методом введения новой переменной:
-
9х⁴-37х²+4=0
-
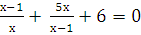
Вариант 4.
-
Решите уравнение:
-
Решите уравнение методом введения новой переменной:
-
9х⁴-10х²+1=0
-
(х²+4х-4)(х²+4х+1)=6
Самостоятельная работа №5.
Вариант 1.
-
Решите уравнение:
-
х²+8х+15=0
-
х²-2х-2=0
-
5х²-8х+3=0
-
Решите задачу. Произведение двух натуральных чисел, одно из которых на 4 больше другого, равно 96. Найти эти числа.
Вариант 2.
-
Решите уравнение:
-
х²-2х-24=0
-
х²+6х+4=0
-
3х²+8х-3=0
-
Решите задачу. Одна из сторон прямоугольника на 6 см больше другой, а его площадь равна 216 см². Найти стороны прямоугольника.
Вариант 3.
-
Решите уравнение:
-
х²+4х-21=0
-
2х²-2х-1=0
-
7х²-4х-3=0
-
Решите задачу. 48 км против течения реки катер проплывает на 48 мин. дольше, чем 56 км по течению реки. Найти скорость течения реки, если собственная скорость катера 12 км/ч.
Вариант 4.
-
Решите уравнение:
-
х²-6х-16=0
-
9х²-6х-1=0
-
7х²-16х-15=0
-
Решите задачу. Поезд был задержан с отправлением на 16 мин. Поэтому, чтобы прибыть в пункт назначения вовремя, он увеличил скорость на 10 км/ч. С какой скоростью двигался поезд, если пройденное им расстояние равно 80 км?
Самостоятельная работа №6.
А 3х²-2х-5=0
Д х²=5
И 7х²+14х=0
Н х²+5х+4=0
О х²+4х+4=0
Т х²-4=0
Ф 2х²-11х+5=0
Е х²+2х=х²+6
Вопросы:
-
Какое уравнение можно решить извлечением квадратных корней?
-
Какое уравнение решается вынесением общего множителя за скобки?
-
Какое уравнение можно решить, представляя в виде квадрата двучлена?
-
В каком уравнении надо применять общую формулу корней?
-
Какое уравнение решается по формуле, используя четный второй коэффициент?
-
Какое уравнение удобно решить по теореме Виета?
-
Какое уравнение можно решить разложением разности квадратов?
Ответы: ДИОФАНТ
Самостоятельная работа №7.
Вариант 1.
-
Выполнить действия:
-
Вычислить:
Вариант 2.
-
Выполнить действия:
-
Вычислить:
Самостоятельная работа №8.
Вариант 1.
-
Сократить дробь:
2. Представьте в виде дроби:
3. Найти значение выражения:
5у² - ![]()
4. Упростить выражение:
![]()
Вариант 2.
-
Сократить дробь:
2. Представьте в виде дроби:
3. Найти значение выражения:
7а² - ![]()
4. Упростить выражение:
![]()
Самостоятельная работа №9.
Вариант 1.
1. Сократить дробь: ![]()
2. Упростить выражение:
3. Найти наименьший общий знаменатель дробей:
4. Указать порядок выполнения действий:
(3,4-1,9)![]() 33,8+3
33,8+3![]()
Вариант 2.
-
Сократить дробь:
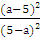
2. Упростить выражение:
3. Найти наименьший общий знаменатель дробей:
4. Указать порядок выполнения действий:
![]() 0,78+1,352
:
0,78+1,352
: ![]()