Конспект урока на тему: СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ (10 класс)

Урок на тему:

СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ

Цель: доказать признак скрещивающихся прямых, теорему о проведении через одну из скрещивающихся прямых плоскости, параллельной другой прямой.

Ход урока

I. Работа над ошибками.

II. Объяснение нового материала. Вспомнить различные случаи взаимного расположения прямых в пространстве.

Рассмотреть различные пары скрещивающихся прямых на моделях многоугольников, наблюдая факт, зафиксированный в признаке скрещивающихся прямых.Например, ABCDA₁B₁C₁D₁ - куб. АА₁ и DC - скрещивающиеся ребра. В каких плоскостях лежит прямая CD? Как располагается прямая АА₁ по отношению к этим плоскостям?

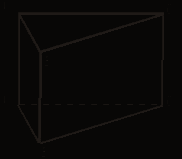
ABCA₁B₁C₁ - призма. ВВ₁ и А₁С₁ - скрещивающиеся ребра. В каких плоскостях лежит прямая ВВ₁? Как располагается прямая А₁С₁ по отношению к этим плоскостям?

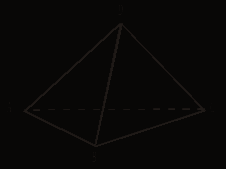
АBCD - пирамида. Рассуждаем аналогично. Наблюдаем: прямые являются скрещивающимися, если одна прямая лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой.

Если учащиеся упустили выделенный в формулировке факт, то привести контрпример - пересекающиеся прямые.

Доказать признак скрещивающихся прямых.

Для «открытия» учащимися факта второй теоремы опять обратиться к рассмотрению моделей, каждый раз отвечая на вопросы: назовите плоскость, проходящую через одну из скрещивающихся прямых параллельно другой прямой? Сколько таких плоскостей?

При рассмотрении третьей модели должна возникнуть проблема - можно ли через одну из скрещивающихся прямых построить плоскость, параллельную другой прямой? Учащимся предлагается построить такую плоскость.Дано: ABCD.

Построить α : АВ α, СD || α.

Анализ

Предположим, что плоскость α построена. Тогда в ней найдется какая-либо прямая MN, параллельная прямой CD. Прямые АВ и MN пересекаются и однозначно определяют плоскость α.

Построение

1. Построить MN AB, MN || CD.

2. (MN, AB) ≡ α.

3. α - единственная.

Таким образом, мы доказали теорему, что через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

III. Решение задач.

№ 34 (решать устно, требовать, чтобы учащиеся проговаривали формулировки признаков).

№ 36.Дано: a || b, c a, c b.

Доказать, что bc.

Чтобы утверждать, что b и c - скрещивающиеся прямые, что надо доказать? (Что одна из них лежит в некоторой плоскости, а другая пересекает эту плоскость.)

Через какие прямые мы можем провести плоскость? (Через пересекающиеся, через параллельные.)

Если мы проведем плоскость α через пересекающиеся прямые а и с, то прямая b, будет параллельна плоскости α. То есть нужно провести плоскость α через параллельные прямые а и b.

1. (a, b) ≡ α.

2.

3. (по признаку).

Домашнее задание: теория (п. 7), № 35 (воспользуйтесь методом от противного), № 37.