Урок алгебры в 9 классе Алгебраические способы решения мудрых задач

Тема: Алгебраические способы решения мудрых старинных задач.

Цели: закрепить знания и умения геометрической прогрессии, применять знания геометрической прогрессии при решении старинных задач, через которые мы учимся быть добрыми, щедрыми, заботливыми.

1. Организационный момент.

Здравствуйте ребята! Здравствуйте наши гости! Давайте, ребята начнём урок с обмена хорошего настроения. Подарим улыбку друг другу и подарим улыбку нашим гостям. Пусть сегодня у всех будет хорошее настроение.

2. Эпиграф: Когда по склонам вечной суеты

Бежать от неудач устанешь люто,

Направь шаги Тропою Доброты

И радость помоги найти кому - то.

И. Романов.

Начать наш необычный урок, я хочу словами:

«Делать людям добро - добреть самому».

Как вы ребята понимаете эти слова? Надо быть хорошим человеком, делать то, что нравится, оставлять добрый след.

Сегодня мы с вами закрепим геометрическую прогрессию и по решаем старинные задачи - посмотрим чему учат эти задачи.

3. Актуализация знаний и умений учащихся:

1) Дать определение геометрической прогрессии

Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число

2) Что нужно знать, чтобы задать геометрическую прогрессию?

Достаточно указать в1 и знаменатель q.

1

Раздать карточки слабым учащимся

3) «Кто быстрее»

По периметру класса развешаны карточки с формулами. По команде «Вперёд» - учащиеся должны найти формулы, относящиеся к геометрической прогрессии.

Подводится итог, правильно или нет, собраны формулы.

4. Применение практическое.

1) Найдите q и в1 геометрической прогрессии, если в5 = 64; в3 = 4

в5:в3 = (в1 * q4):(в1 *q2) = q2; 64:4=16; q2=16; q=4;

в3=в1*q2; 4 = в1 * 16;

в1 = 4 / 16 = 1 /4

2) Для геометрической прогрессии вn = 4 * 2n - 1. Найдите в2 и в5

в2 = 4 * 22-1 = 4 * 2 =8; в5 = 4 * 25-1 = 4 * 24 = 4 * 16 = 64

3) Известно в2 = 1, в4 = 9. Найдите в3, в1.

в4:в2 = (в1 * q3):(в1 * q) = q2; 9:1 = 9; q2 = 9; q = 3;

в2 = в1 * q; в1 = 1 / 3; в3 = в1 * q2 = 1/3 * 9 = 3.

Y. Сообщение учащегося «числа Фибоначчи»

Мы мало знаем о великих математиках, учёных. Которые внесли большую лепту в развитие математики. Оля Качина познакомит нас с сообщением «числа Фибоначчи», кто это за учёный и что он сделал для математики.

YI. Решение задач.

В стариной «Арифметике» Магницкого (которой в 2003г. Исполнилось 300 лет) приведена следующая задача:

1) Некто продал лошадь за 156 рублей. Но покупатель, приобретая лошадь, раздумал её покупать и возвратил продавцу, говоря:

- Нет мне расчета, покупать за эту цену лошадь, которая таких денег не стоит.

2

Тогда продавец предложил другие условия:

- Если, по - твоему, цена лошади высока, то купи только её подковные гвозди, лошадь же тогда получишь в придачу бесплатно. Гвоздей в подкове шесть. За первый гвоздь дай мне всего 1/4 копейки, за второй 1/2 копейки, за третий 1 копейку и т. д.

Покупатель, соблазненный низкой ценой и желая даром получить лошадь, принял условия продавца, рассчитывая, что за гвозди придётся уплатить не более 10 рублей. Так ли это?

Составим последовательность из 24 чисел:

1/4; 1/2; 1; 2; 22; 23;…;221.

Данная последовательность является геометрической прогрессией.

В1 = 1/4; в2 = 1/2; q = 2

Чтобы узнать заплаченную цену, надо найти сумму чисел.

Вывод: скупой платит дважды. Жадность, алчность сыграли злую шутку с покупателем.

3

Зарядка для глаз: вдаль «т» и себе на нос…

2) «легенда о создателе шахмат»:

По преданию, индийский принц Серам восхищённый игрой, призвал к себе её создателя, учёного Сету, и сказал:

- Я желаю достойно наградить тебя за прекрасную игру. Я достаточно богат, чтобы исполнить любое твоё желание.

Сета попросил принца положить на первую клетку шахматной доски 1 зерно, на вторую 2 зерна, на третью 4 зерна и т. д.

Смог ли принц Серам выполнить желание Сеты?

Решение:

1; 2; 4; …

В1 = 1; в2 = 2; q = 2. Всё ли вам нравится? Нет ли здесь подвоха? «Найди ошибку»

(18 квинтиллионов 446 квадриллионов 744 триллиона

73 миллиарда 709 миллионов 551 тысяча 615 зерен)

Ответ: больше триллиона тонн

Вывод: не обещай того, что не сможешь выполнить. Не будь заносчивым, самоуверенным. Бедный, но умный.

3) Задача на убывающую геометрическую прогрессию.

Дан квадрат, сторона которого равна 4 см. Середины его сторон являются вершинами второго квадрата, середины сторон второго квадрата являются вершинами третьего квадрата и т. д.

4

Найти сумму площадей всех квадратов.

Решение:

Ясно, что площадь каждого следующего квадрата равна половине площади предыдущего. Значит, последовательность площадей квадратов является геометрической прогрессией.

Первый член, которой равен 16, второй член равен 8, знаменатель равен 1/2.

Найдём сумму этой геометрической прогрессии

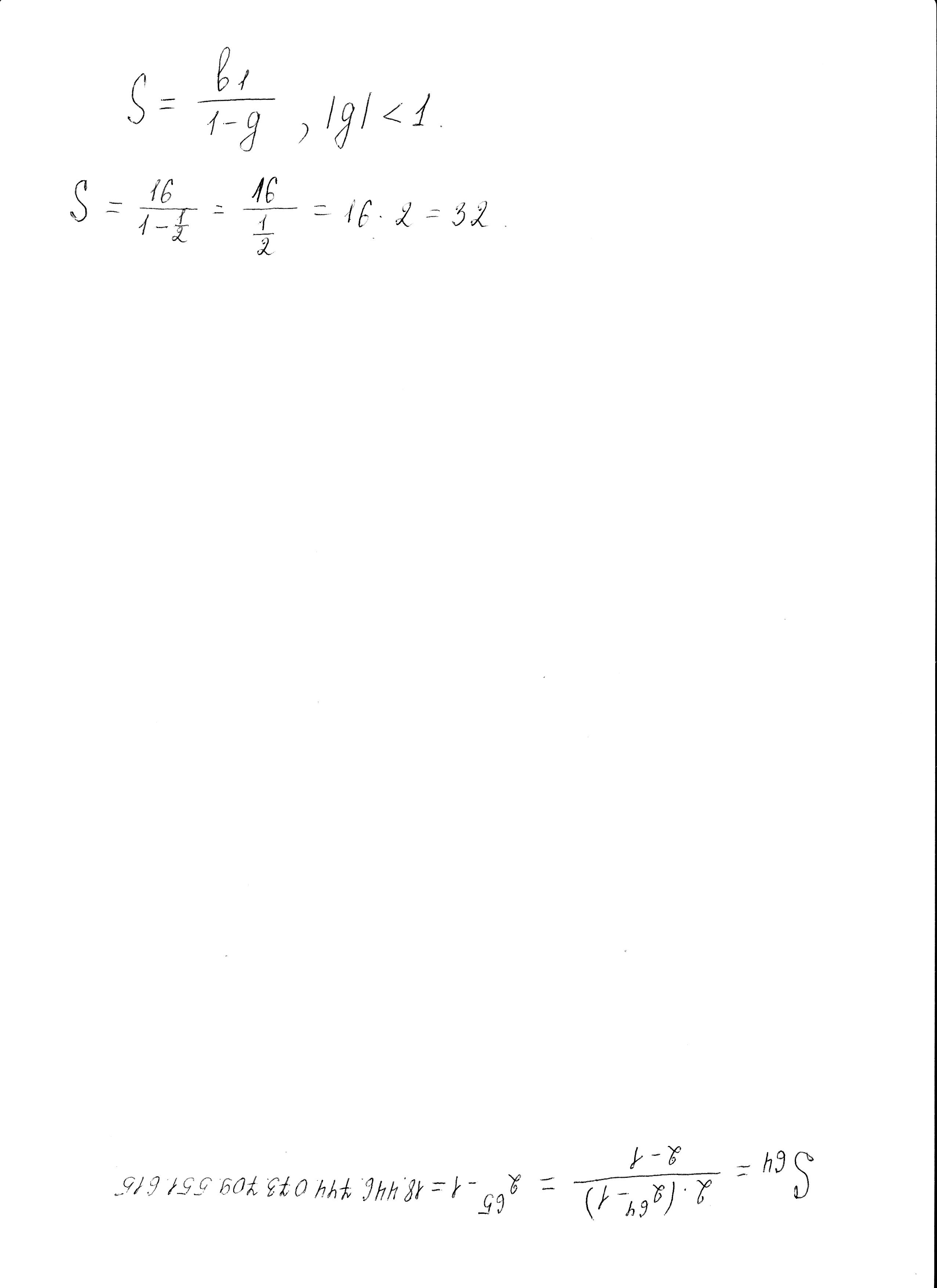
Ответ: сумма геометрической прогрессии равна 32 см².

YII. Диктант.

Вариант 1.

Вариант 2.

1. У геометрической прогрессии первый член равен 8, второй член 4. Найти знаменатель q.

1. У геометрической прогрессии первый член равен 9, второй член 3. Найти знаменатель q

2. У геометрической прогрессии первый член равен 9, второй член 3. Найти b3

2. У геометрической прогрессии первый член равен 8, второй член 4. Найти b3

3. Найдите четвёртый член геометрической прогрессии, если её первый член равен 1, а знаменатель q = -2.

3. Найдите шестой член геометрической прогрессии, если её первый член равен 1, а знаменатель q = -2.

Ответ:

Вариант 1.

Вариант 2.

1. b1=8, b2=4

q=4/8=1/2

1. b1=9, b2=3

q=3/9=1/3

2. b1=9, b2=3, b3=?

q=3/9=1/3

b3=b1*q2=9*(1/3)2=1

2. b1=8, b2=4, b3=?

q=4/8=1/2 b3=b1*q2=8*(1/2)2=2

3. b1=1, q=-2, b4=?

b4=b1*q3 =1*(-2)3=-8

3. b1=1, q=-2, b6=?

b6=b1*q5 =1*(-2)5=-32

YIII. Итог урока:

Сегодня мы увидели, как в жизненных ситуациях, всегда оставаться порядочными людьми: добрыми, правдивыми, искренними …

Любая старинная задача учит не только математике, но и смыслу жизни.

Понравился урок? Как настроение? Кому за урок скажем спасибо?

Я вас тоже благодарю.

Спасибо всем!

6