- Учителю
- Рабочая программа геометрия 9 класс по учебнику А.В. Погорелова
Рабочая программа геометрия 9 класс по учебнику А.В. Погорелова
МКОУ Стрелковская средняя общеобразовательная школа
п. Стрелка-Чуня
Эвенкийского района
на методическом совете
«_31__» _августа__ 2016 г.
УТВЕРЖДАЮ
Директор школы
Шипицын В.П.
Приказ №__________ от «____» _________ 2016 г.
Рабочая программа
по геометрии
9 класс
Составил: учитель математики А.В. Тарасенко
2016- 2017 учебный год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Нормативные правовые документы, на основании которых разработана рабочая программа:
-
Федеральный компонент государственного образовательного стандарта, утвержденный Приказом Минобразования РФ № 1089 от 05.03.2004;
-
Примерные программы, созданные на основе федерального компонента государственного образовательного стандарта, рекомендованные Министерством образования и науки РФ приказ № 03-1263 от 07.07.2005.
-
Базисный учебный план общеобразовательных учреждений Российской Федерации, утвержденный приказом Минобразования РФ № 1312 от 09.03.2004;
Данная рабочая программа разработана на основе типовой государственной программы для общеобразовательных школ, гимназий, лицеев. Математика. Составители: Г.М. Кузнецова, Н.Г. Миндюк. Рекомендовано Департаментом образовательных программ и стандартов общего образования Министерства образования Российской Федерации, 2001 год. Использовалась программа общеобразовательных учреждений ГЕОМЕТРИЯ 7-9 классы. Составитель: Т.А. Бурмистрова. Москва «Просвещение», 2009 год.
Типовая государственная программа по математике в 9 классе рассчитана на 5 часов в неделю, 170 часов в год. В соответствии с Учебным планом МКОУ Стрелковская СОШ на изучение математики в 9 классе выделено 5 часов в неделю, 170 часа в год (3 часа в неделю - алгебра, 2 часа в неделю - геометрия).
Место предмета в федеральном базисном плане:
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики на ступени основного общего образования отводится не менее 875 ч. из расчета 5 ч. в неделю с 5 по 9 класс.
Приведено тематическое планирование по II варианту: 2 часа в неделю, всего 68 чаcов..
Промежуточная аттестация проводится в форме самостоятельных, проверочных работ в конце логически законченных блоков учебного материала. Итоговая аттестация предусмотрена в виде контрольных работ.
Уровень обучения - базовый.
Программа соответствует учебнику «Геометрия 7-9 класс» / А.В. Погорелов - Москва: «Просвещение» 2014 г.
Количество часов в год: 68
Уровень рабочей программы: базовый
Цели и задачи рабочей программы
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Целью изучения курса геометрии в 7-9 классах является систематическое изучение свойств геометрических фигур на плоскости, формирование пространственных представлений развитие логического мышления и подготовка аппарата, необходимого для изучения смежных дисциплин (физика, черчение и др.) и курса стереометрии в старших классах.
Курс характеризуется рациональным сочетанием логической строгости и геометрической наглядности. Увеличивается теоретическая значимость изучаемого материала, расширяются внутренние логические связи курса, повышается роль дедукции, степень абстрактности изучаемого материала. Учащиеся овладевают приёмами аналитико-синтетической деятельности при доказательстве теорем и решении задач. Систематическое изложение курса позволяет начать работу по формированию представлений учащихся о строении математической теории, обеспечивает развитие логического мышления школьников. Изложение материала характеризуется постоянным обращением к наглядности, использованием рисунков и чертежей на всех этапах обучения и развитием геометрической интуиции на этой основе. Целенаправленное обращение к примерам из практики развивает умения учащихся вычленять геометрические факты, формы и отношения в предметах и явлениях действительности, использовать язык геометрии для их описания.
В результате изучения геометрии ученик должен
знать/понимать:
-
существо понятия математического доказательства; приводить примеры доказательств;
-
существо понятия алгоритма; приводить примеры алгоритмов;
-
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
-
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
уметь:
-
пользоваться геометрическим языком для описания предметов окружающего мира;
-
распознавать геометрические фигуры, различать их взаимное расположение;
-
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
-
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
-
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
-
вычислять значения геометрических величин (длин, углов, площадей, объемов); в том числе определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
-
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
-
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
-
решать простейшие планиметрические задачи в пространстве;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
описания реальных ситуаций на языке геометрии;
-
расчетов, включающих простейшие тригонометрические формулы;
-
решения геометрических задач с использованием тригонометрии;
-
решения практических задач, связанных с нахождением геометрических величин
-
( используя при необходимости справочники и технические средства );
построение геометрическими инструментами ( линейка, угольник, циркуль, транспортир).
Представленная программа выполняет две основные функции.
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся 9 класса средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Литература:
-
Погорелов А.В. «Геометрия 7-9». Учебник для 7-9 классов общеобразовательных учреждений- М., Просвещение, 2004;
-
«Методические рекомендации к курсу геометрии 6-8 классов», Москва: «Просвещение», 1987г.
-
А.И. Медяник «Контрольные и проверочные работы по геометрии 7-11 классы», Москва: Дрофа 2002 г.
-
А.И. Азевич «Задачи по геометрии 7-9 классы. Дидактические материалы и контрольные работы», Москва: «Школьная Пресса», 2003г.
-
Б.Г. Зив, В.М. Мейлер, А.Г. Баханский «Задачи по геометрии для 7-11 классов», Москва: «Просвещение», 1991г.
-
CD - Дидактический и раздаточный материал «Геометрия 7-9 классы», Издательство «Учитель»
-
Периодические издания (учебно-методическая газета «математика» - издательство «1 сентября», научно-методический журнал «Математика в школе» - издательство ООО «Школьная Пресса», научно-методический журнал «Математика. Все для учителя» - издательская группа «Основа»);
-
Геометрия: Задачи на готовых чертежах. 7-9 классы./ Составитель: М.Р. Рыбникова. -Луганск. «Учебная книга», 2007г.
СОДЕРЖАНИЕ ТЕМ УЧЕБНОГО КУРСА
-
Подобие фигур
Понятие о гомотетии и подобии фигур. Подобие треугольников. Признаки подобия треугольников. Подобие прямоугольных треугольников. Центральные и вписанные углы и их свойства.
Основная цель. - усвоить признаки подобия треугольников и отработать навыки их применения.
-
Решение треугольников.
Теорема синусов и косинусов. Решение треугольников.
Основная цель - познакомить учащихся с основными алгоритмами решения произвольных треугольников.
-
Многоугольники.
Ломаная. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Правильные многоугольники. Окружность, вписанная в правильный многоугольник. Окружность, описанная около правильного многоугольника. Длина окружности. Длина дуги окружности. Радианная мера угла.
Основная цель - расширить, систематизировать сведения о многоугольниках и окружностях.
-
Площади фигур.
Площадь и ее свойства. Площади прямоугольника, треугольника, параллелограмма, трапеции. Площадь круга и его частей.
Основная цель - сформировать у учащихся общее представление о площади и умение вычислять площади фигур.
-
Элементы стереометрии.
Аксиомы стереометрии. Параллельность и перпендикулярность прямых и плоскостей в пространстве. Многогранники. Тела вращения.
Основная цель - дать начальное представление о телах и поверхностях в пространстве, о расположении прямых и плоскостей в пространстве.
-
Обобщающее повторение курса планиметрии.
Содержание тем учебного курса
68
68
5
|
1 |
2 |
3 |
4 |
5 |
6 |
|
дата |
Кол-во часов |
Тема урока |
Ученик должен знать: |
Ученик должен уметь: |
Вид контроля |
|
Подобие фигур - 15 ч. | |||||
|
|
1 |
Понятие гомотетии и подобии фигур |
- определение гомотетии, подобия, коэффициентов гомотетии и подобия; - определение подобных фигур; - формулировки признаков подобия треугольников; - определение центрального угла; - определение угла, вписанного в окружность. |
- доказывать свойство о сохранении углов при преобразованиях подобия; - воспроизводить доказательства признаков подобия; - применять признаки подобия при решении задач; - доказывать теорему о вписанном угле; - доказывать свойства отрезков хорд и секущих окружности; - решать задачи на применение свойства вписанного угла. |
|
|
|
1 |
Свойства преобразования |
Текущий | ||
|
|
2 |
I признак подобия треугольников |
Текущий, индивидуальный | ||
|
|
2 |
II признак подобия треугольников |
Текущий, индивидуальный | ||
|
|
2 |
III признак подобия треугольников |
Текущий, индивидуальный | ||
|
|
2 |
Подобие прямоугольных треугольников |
Текущий, индивидуальный | ||
|
|
1 |
Углы, вписанные в окружность. |
Текущий, индивидуальный | ||
|
|
2 |
Пропорциональность отрезков, хорд и секущих. |
Текущий, индивидуальный | ||
|
|
1 |
Урок - зачет |
|
|
Тестирование |
|
|
1 |
Контрольная работа №1 |
|
|
Индивидуальный |
|
Решение треугольников - 11 ч. | |||||
|
|
2 |
Теорема косинусов. |
- формулировку теоремы косинусов и следствия из нее; Утверждения о свойствах диагоналей параллелограмма; - формулировки теоремы синусов и следствия из нее о соотношении между сторонами и углами треугольника; - что значит решить треугольник; - четыре типа задач: по данной стороне и двум углам; по двум сторонам и углу между ними; по двум сторонам и углу, противолежащему одной из них; по трем сторонам. |
- доказывать теорему косинусов; - записывать в виде равенства теорему косинусов применительно к данному треугольнику; - применять теорему косинусов; - доказывать теорему синусов; - записывать ее формулировку к любому треугольнику; - составлять пропорции для сторон и углов данного треугольника; - применять ее при решении задач; - решать задачи четырех типов; - для каждой из трех основных задач проводить решение в общем виде и для конкретных треугольников. |
Текущий, индивидуальный |
|
|
3 |
Теорема синусов. |
Текущий, индивидуальный | ||
|
|
4 |
Решение треугольников. |
Текущий, самостоятельная работа | ||
|
|
1 |
Урок -зачет |
|
|
Тестирование |
|
|
1 |
Контрольная работа №2 |
|
|
Индивидуальный |
|
Многоугольники - 13ч. | |||||
|
|
1 |
Ломаная. |
- что длина ломаной не меньше длины отрезка, соединяющего его концы; - сумма углов выпуклого n - угольника равна 1800(n-2), а сумма внешних углов - 3600; - для каждого правильного многоугольника существует окружность, вписанная в него, и окружность, описанная около него; - существуют формулы, связывающие радиус описанной окружности и радиус вписанной окружности со стороной a правильного n - угольника для n=3. n=4. n=6; - периметры правильных n - угольников
относятся как радиусы описанных (вписанных) окружностей,
|
- изображать ломаную, называть по рисунку ее элементы, проводить доказательство теоремы; - чертить многоугольник (выпуклый), строить его диагонали, внешние углы, уметь доказывать теорему о сумме углов выпуклого многоугольника; - выводить формулу
- применять формулу длины окружности для решения задач. |
Текущий |
|
|
1 |
Выпуклые многоугольники. |
Текущий | ||
|
|
1 |
Правильные многоугольники. |
Текущий | ||
|
|
3 |
Формулы для радиусов вписанных и описанных окружностей. |
Текущий, индивидуальный | ||
|
|
1 |
Построение правильных выпуклых многоугольников. |
Текущий | ||
|
|
1 |
Подобие правильных выпуклых многоугольников. |
Текущий, индивидуальный | ||
|
|
3 |
Длина окружности. Радианная мера угла. |
Текущий, индивидуальный, самостоятельная работа | ||
|
|
1 |
Урок -зачет |
|
|
Тестирование |
|
|
1 |
Контрольная работа №3 |
|
|
Индивидуальный |
|
Площади - 15ч. | |||||
|
|
2 |
Понятие площади. Площадь прямоугольника. |
- свойства площади; - формулу площади прямоугольника, треугольника, параллелограмма, трапеции; - формулы, связывающие площадь треугольника и радиусы вписанных и описанных окружностей; - что площади подобных фигур относятся как квадраты линейных размеров; - определение круга, кругового сегмента, кругового сектора; - формулу площади круга, кругового сектора, кругового сегмента. |
- выводить формулу площади прямоугольника; - проводить доказательство справедливости формул площадей; - находить отношение площадей подобных фигур по известным длинам пары соответствующих элементов этих фигур; - находить площадь круга, распознавать и изображать круговой сектор и круговой сегмент, вычислять их площади; - применять все известные формулы при решении задач. |
Текущий, индивидуальный |
|
|
2 |
Площадь параллелограмма. |
Текущий, индивидуальный | ||
|
|
2 |
Площадь треугольника. |
Текущий, индивидуальный | ||
|
|
2 |
Площадь трапеции. |
Текущий, индивидуальный | ||
|
|
2 |
Формулы для радиусов вписанной и описанной окружностей треугольника. |
Текущий, индивидуальный | ||
|
|
1 |
Площади подобных фигур. |
Текущий, индивидуальный | ||
|
|
2 |
Площадь круга и его частей. |
Текущий, индивидуальный | ||
|
|
1 |
Урок -зачет |
|
|
Тестирование |
|
|
1 |
Контрольная работа №4 |
|
|
Индивидуальный |
|
Обобщающее повторение курса планиметрии - 9 ч. | |||||
|
|
1 |
Углы. Параллельные прямые. Перпендикулярные прямые. |
|
|
|
|
|
2 |
Треугольники. |
|
|
|
|
|
2 |
Четырехугольники. |
|
|
|
|
|
1 |
Многоугольники. Окружность. Круг. |
|
|
|
|
|
1 |
Преобразование фигур. |
|
|
|
|
|
1 |
Векторы на плоскости. |
|
|
|
|
|
1 |
Итоговая контрольная работа |
|
|
Индивидуальный |
|
Введение в стереометрию - 5ч. | |||||
|
|
2 |
Строение геометрии. Аксиомы стереометрии. |
|
|
|
|
|
1 |
Многогранники. |
| ||
|
|
1 |
Тела вращения. |
| ||
|
|
1 |
Итоговый урок |
|
|
|
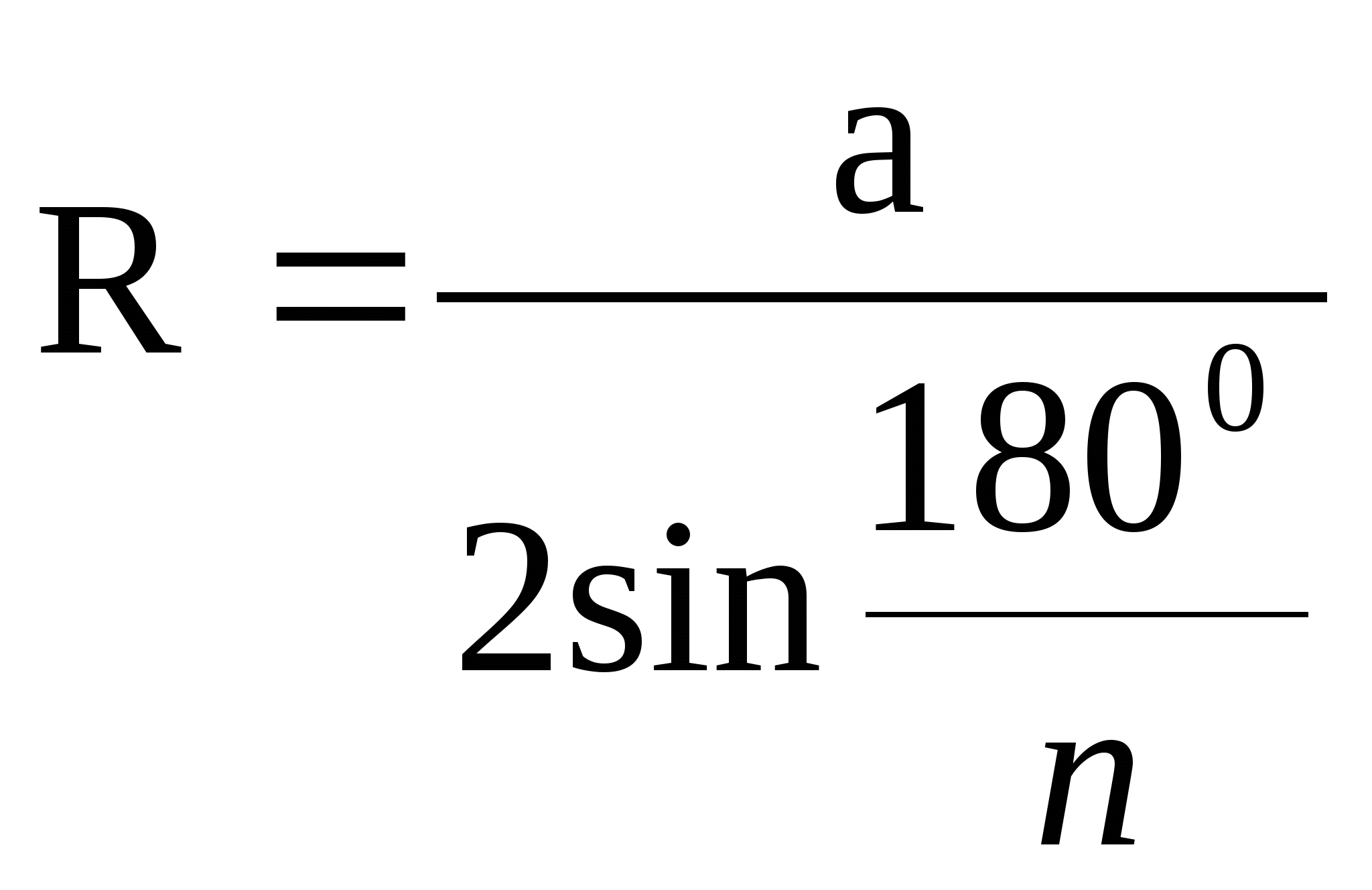 ,
n =
,
n = 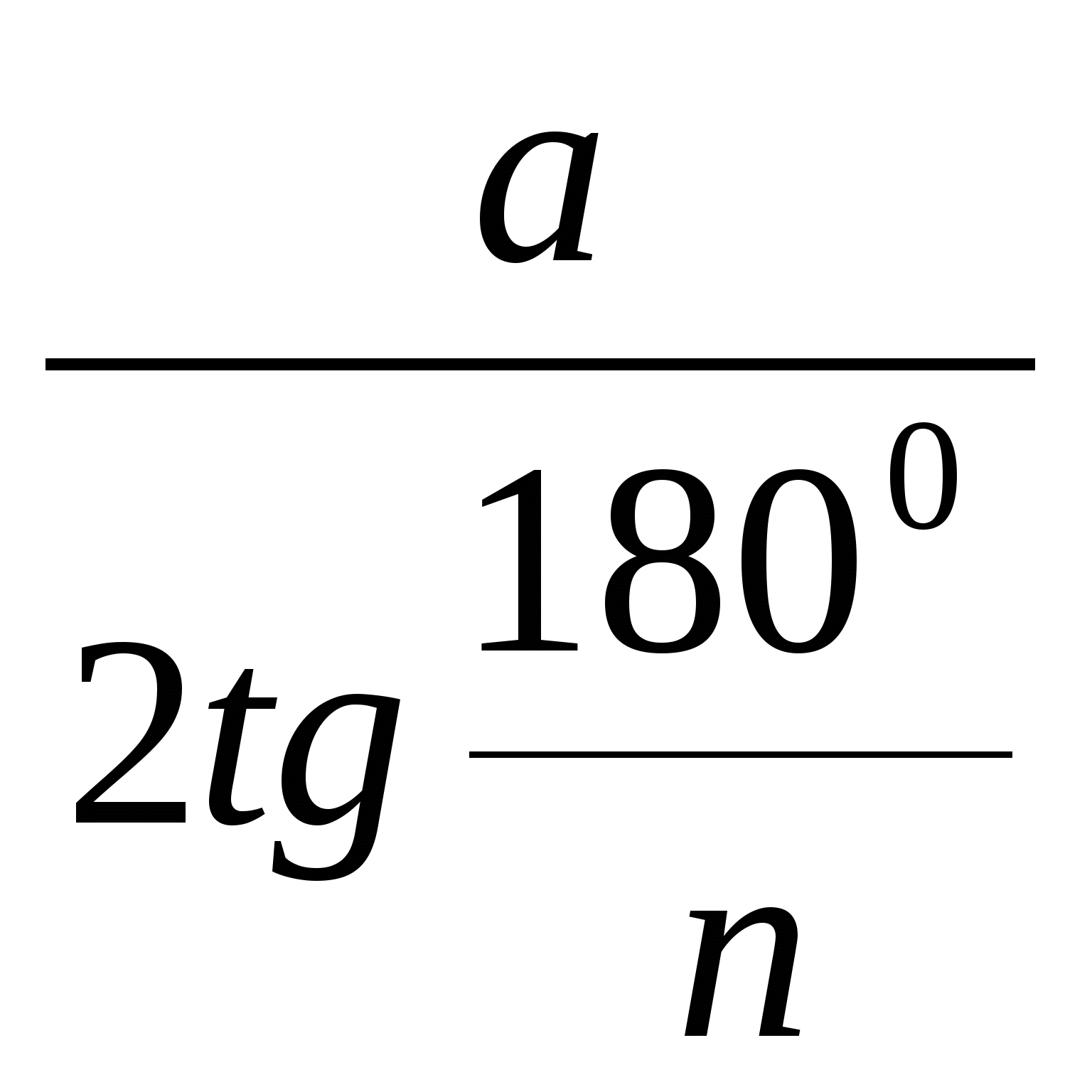 ;
;