- Учителю
- Разработка урока внеурочной деятельности Мозаика
Разработка урока внеурочной деятельности Мозаика
Урок № 53 - 55
Логика 5 класс
Тема: «Знакомство с математической мозаикой. Математическая мозаика».
Целеполагания:
-
познакомить ребят с понятиями математическая мозаика и мозаика;
-
научить их решать такие задачи;
-
научить их составлять математические мозаики;
-
способствовать развитию умений анализировать, сравнивать, обобщать, выделять главное; развивать осознанную математическую речь; развитие познавательного интереса учащихся;
-
содействовать воспитанию таких качеств как: самостоятельность, целеустремленность, настойчивость, целенаправленность, трудолюбие, аккуратность, ответственность
Задачи:
- Продолжить формирование навыков контроля результатов деятельности.
- Способствовать развитию коммуникативных навыков. Развивать умение анализировать, обобщать материал, выступать перед аудиторией, развивать интеллектуальные, творческие и исследовательские способности, активизировать интерес к учебным предметам.
- Формирование логического, абстрактного, эвристического, системного мышления.
Оборудование: проектор, экран, компьютер, презентации
План.
-
Организационные моменты.
Сообщение темы и целей урока.
-
Что такое математическая мозаика и ее виды.
Математическое искусство М.К. Эшера
Голландский художник Мориц Корнилис Эшер, родившийся в 1898 году в Леувардене создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей.
Когда он учился в школе, родители планировали, что он станет архитектором, но плохое здоровье не позволило Морицу закончить образование, и он стал художником. До начала 50-х годов он не был широко известен, но после ряда выставок и статей в американских журналах (Time и др.) он получает мировую известность. Среди его восторженных поклонников были и математики, которые видели в его работах оригинальную визуальную интерпретацию некоторых математических законов. Это более интересно тем, что сам Эшер не имел специального математического образования.
В процессе своей работы он черпал идеи из математических статьей, в которых рассказывалось о мозаичном разбиении плоскости, проецировании трехмерных фигур на плоскость и неевклидовой геометрии, о чем будет рассказываться ниже. Он был очарован всевозможными парадоксами и в том числе "невозможными фигурами". Парадоксальные идеи Роджера Пенроуза были использованы во многих работах Эшера. Наиболее интересными для изучения идеями Эшера являются всевозможные разбиения плоскости и логика трехмерного пространства.
Мозаики
Эскиз из Альгамбры
Регулярное разбиение плоскости, называемое "мозаикой" - это набор замкнутых фигур, которыми можно замостить плоскость без пересечений фигур и щелей между ними. Обычно в качестве фигуры для составления мозаики используют простые многоугольники, например, квадраты или прямоугольники. Но Эшер интересовался всеми видами мозаик - регулярными и нерегулярными (прим. перев. нерегулярные мозаики образуют неповоряющиеся узоры) - а также ввел собственный вид, который назвал "метаморфозами", где фигуры изменяются и взаимодействуют друг с другом, а иногда изменяют и саму плоскость.
Интересоваться мозаиками Эшер начал в 1936 году во время путешествия по Испании. Он провел много времени в Альгамбре, зарисовывая арабские мозаики, и впоследствии сказал, что это было для него "богатейшим источником вдохновения". Позже в 1957 году в своем эссе о мозаиках Эшер написал:
В математических работах регулярное разбиение плоскости рассматривается теоретически... Значит ли это, что данный вопрос является сугубо математическим? Математики открыли дверь ведущую в другой мир, но сами войти в этот мир не решились. Их больше интересует путь, на котором стоит дверь, чем сад, лежащий за ней.
Математики доказали, что для регулярного разбиения плоскости подходят только три правильных многоугольника: треугольник, квадрат и шестиугольник. (Нерегулярных вариантов разбиения плоскости гораздо больше. В частности в мозаиках иногда используются нерегулярные мозаики, в основу которых положен правильный пятиугольник.) Эшер использовал базовые образцы мозаик, применяя к ним трансформации, которые в геометрии называются симметрией, отражение, смещение и др. Также он исказил базовые фигуры, превратив их в животных, птиц, ящериц и проч. Эти искаженные образцы мозаик имели трех-, четырех- и шестинаправленную симметрию, таким образом сохраняя свойство заполнения плоскости без перекрытий и щелей.
Регулярное разбиение
плоскости птицами

Рептилии

Цикл

Эволюция 1
В гравюре "Рептилии" маленькие крокодилы играючи вырываются из тюрьмы двухмерного пространства стола, проходят кругом, чтобы снова превратиться в двухмерные фигуры. Мозаику рептилий Эшер использовал во многих своих работах. В "Эволюции 1" можно проследить развитие искажения квадратной мозаики в центральную фигуру из четырех ящериц.
Многогранники
Четыре правильных
многогранника
Правильные геометрические тела - многогранники - имели особое
очарование для Эшера. Во его многих работах многогранники являются
главной фигурой и в еще большем количестве работ они встречаются в
качестве вспомогательных элементов. Существует лишь пять правильных
многогранников, то есть таких тел, все грани которых состоят из
одинаковых правильных многоугольников. Они еще называются телами
Платона. Это - тетраэдр, гранями которого являются четыре
правильных треугольника, куб с шестью квадратными гранями, октаэдр,
имеющий восемь треугольных граней, додекаэдр, гранями которого
являются двенадцать правильных пятиугольников, и икосаэдр с
двадцатью треугольными гранями. На гравюре "Четыре тела" Эшер
изобразил пересечение основных правильных многогранников,
расположенных на одной оси симметрии, кроме этого многогранники
выглядят полупрозрачными, и сквозь любой из них можно увидеть
остальные.
Порядок и хаос
Большое количество различных многогранников может быть получено
объединением правильных многогранников, а также превращением
многогранника в звезду. Для преобразования многогранника в звезду
необходимо заменить каждую его грань пирамидой, основанием которой
является грань многогранника. Изящный пример звездчатого додекаэдра
можно найти в работе "Порядок и хаос". В данном случае звездчатый
многогранник помещен внутрь стеклянной сферы. Аскетичная красота
этой конструкции контрастирует с беспорядочно разбросанным по столу
мусором. Заметим также, что анализируя картину можно догадаться о
природе источника света для всей композиции - это окно, которое
отражается левой верхней части сферы.
Звезды
Фигуры, полученные объединением правильных многогранников, можно встретить во многих работах Эшера. Наиболее интересной среди них является гравюра "Звезды", на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры. Таким образом нам необходимо отвлечься от привычного восприятия картины и попытаться взглянуть на нее свежим взором, чтобы представить ее целиком. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством Эшера.
-
Математические мозаики: придумываем паркет
Урок № 1.
Сегодня поделюсь интересной математической «игрой-уроком-исследованием». Люблю такие математические штуки, про которые нельзя однозначно сказать, что это такое: похоже на игру, потому что весело и интересно; похоже на исследование, потому что любопытно и вначале не ясно что же получится; похоже на урок, потому что находишь новые знания.
Вот и эта тема из такой серии. «Что такое паркет?» Самые частые ответы: пол, там, где танцуют или выступают, покрытие пола. Оказывается, понятие паркета есть и в геометрии - это замощение плоскости одинаковыми многоугольниками без пробелов и перекрытий.

Складыванием паркетов, а самое главное их придумыванием мы и буднм заниматься.
Что интересненького можно придумать?
![]() Начать надо с
рассматривания разных паркетов. Самыми необычные паркетные узоры -
это паркеты Мориса Эшера. В интернете таких картинок очень много,
вот хотя бы несколько:
Начать надо с
рассматривания разных паркетов. Самыми необычные паркетные узоры -
это паркеты Мориса Эшера. В интернете таких картинок очень много,
вот хотя бы несколько:

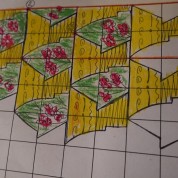
![]() Раскрашиванием
паркета Эшера.
Раскрашиванием
паркета Эшера. 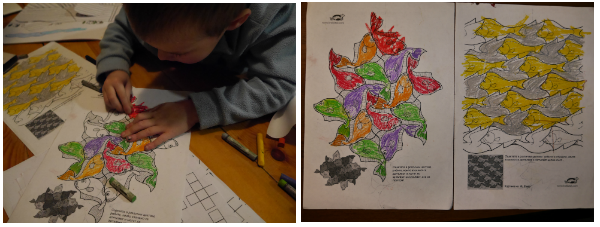
![]() Складывание по
рисунку и без. Здесь основная сложность вырезать много одинаковых
фигурок из картона… Дело можно упростить, если напечатать рисунок
на бумаге, заламинировать и потом вырезать.
Складывание по
рисунку и без. Здесь основная сложность вырезать много одинаковых
фигурок из картона… Дело можно упростить, если напечатать рисунок
на бумаге, заламинировать и потом вырезать. 
Благодаря этому, в короткий срок у меня было много разных качественных мозаик.
Школьники уже могут догадаться, как сложить паркет без схемы. Это непростая задача: найти одинаковые выступы и выемки.
Урок № 2.
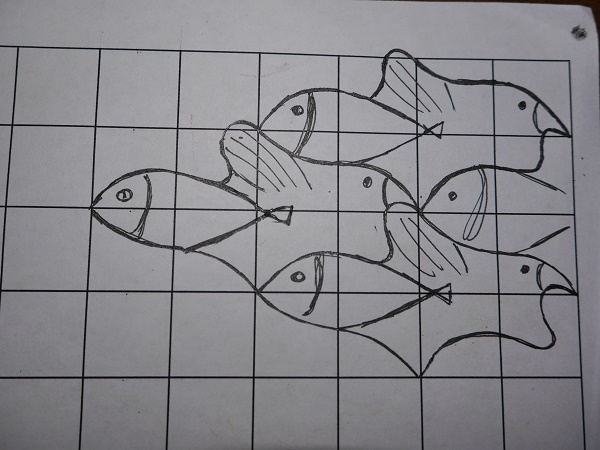
![]() Придумывание и
рисование собственного паркета. Это, пожалуй, самое захватывающее
занятие.
Придумывание и
рисование собственного паркета. Это, пожалуй, самое захватывающее
занятие.
Создание паркета по следующим правилам:
Находим лист в клеточку. Для первой работы, я настоятельно рекомендую распечатать вот эти крупные клетки</<font face="Georgia, serif">. Можно работать и на обычной, мелкой клетке, но тогда надо разделять большие квадратно-прямоугольные области и создавать свою крупную клетку. Примерно так:
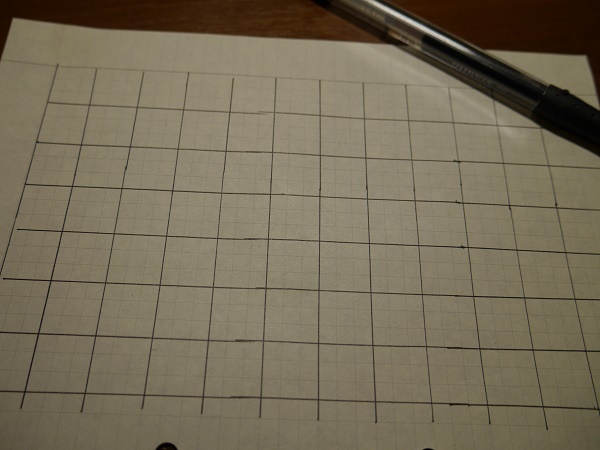 Выбираем любой
правильный контур. Конечно, это могут быть и ромбики, и
шестиугольники - любая правильная фигура из которой уже
складывается простейший паркет. Но мы берем самое простое: квадрат
или прямоугольник.
Выбираем любой
правильный контур. Конечно, это могут быть и ромбики, и
шестиугольники - любая правильная фигура из которой уже
складывается простейший паркет. Но мы берем самое простое: квадрат
или прямоугольник.


Обозначаем 4 точки в вершинах нашей фигуры.
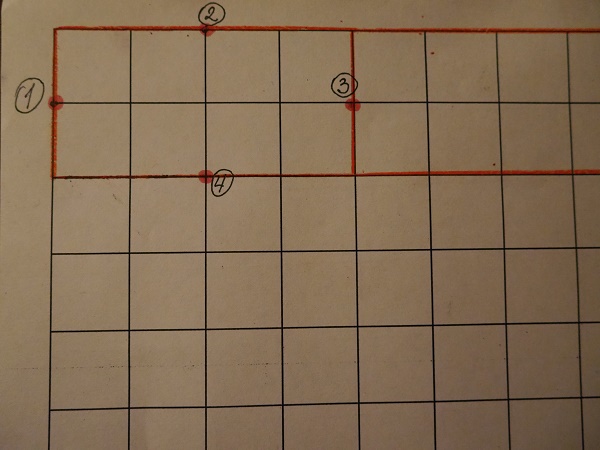
Соединяем точки 1 и 2 любой линией. Делаем параллельный перенос и
соединяем точки 3 и 4 такой же линией. Обращаю внимание: именно
параллельный перенос, а не симметричное отражение.
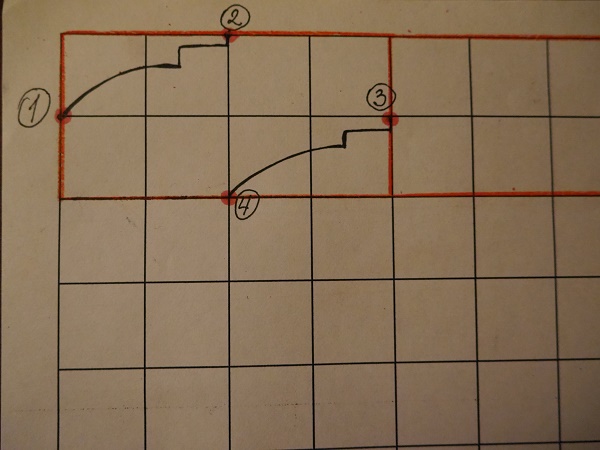
То же самое проделываем с точками 2 и 3. Затем переносим линию
между точками 1 и 4.
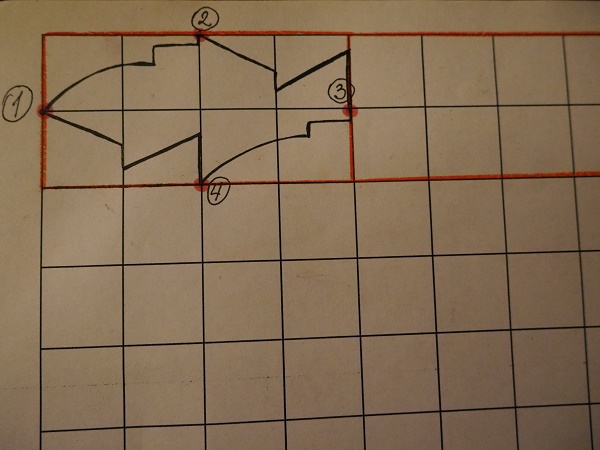
Повторяем работы на соседних клетках.
Придумываем на что похожа наша фигура и создаем образ.
* Небольшая подсказка: нашу фигуру можно разделить на две (3, 4, 5
фигур) произвольным образом. Тогда паркет будет выкладываться из
нескольких разных форм.
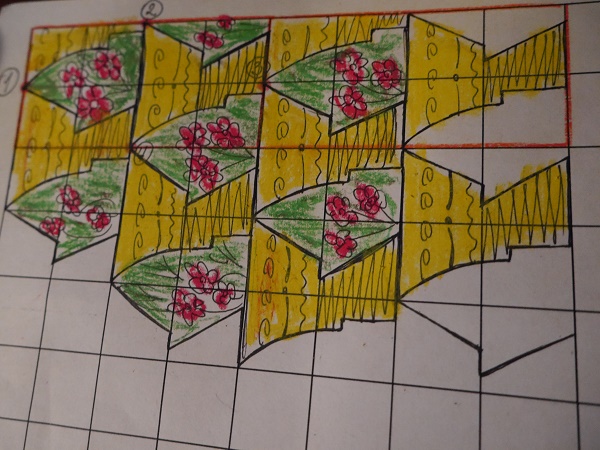
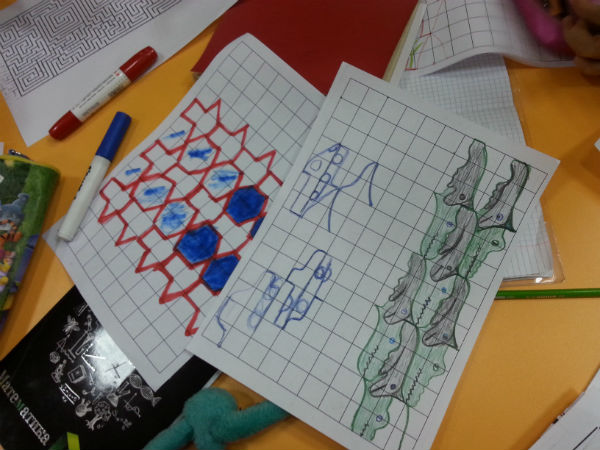
Вот и, всё!
Попробуйте: создание паркетов - одно из интереснейших занятий в котором переплетается математика и творчество, строгость и произвольность, гармония и красота.
Урок № 3. Продолжить создание своего паркета.
-
Итоги урока
Подобная динамика работы с задачами, основанная на идеях укрупнения дидактических единиц, раскрывает и приводит в действие большие резервы человеческого мозга, развивает интеллектуальную сферу ученика.
Очень важно подобрать посильные для обучающихся задания, соответствующие их возможностям, развитию. Ведь часто бывает, что даже смышленый обучающийся не хочет просто прочитать задачу, не то что решать ее, а поэтому целесообразно использовать внешнюю занимательность текстов. Цель может быть достигнута, если условие задачи будет похоже на сказку.
14