- Учителю
- Разработка урока по теме Свойства степени с целым показателем. Урок второй
Разработка урока по теме Свойства степени с целым показателем. Урок второй
Урок № 89
</ Тема: «Свойства степени с целым показателем».
Цели:
-
Продолжить формировать умения применять свойства степени с целым показателем;
-
Повторение:
-
Подготовка к ГИА;
-
Развивать память, внимание, логическое мышление обучающихся;
-
Вырабатывать трудолюбие и целеустремленность обучающихся.
Ход урока.
-
Организационный момент.
Сообщение темы и целей урока.
-
Актуализация знаний и умений обучающихся.
-
Проверка выполнения домашнего задания. (Разбор нерешенных заданий).
-
Повторение - Функция , её график и свойства.
Заметить, что в данной формуле величины
находятся в обратно пропорциональной зависимости, поэтому функцию y
= 
называют обратной пропорциональностью.
На доску выносится з а п и с ь:
.
Подробно остановиться на вопросе построения
графика функции
y = 
. По этому графику описать некоторые свойства функции. Затем
построить график функции y = 
и сопоставить его с графиком функции y =
.
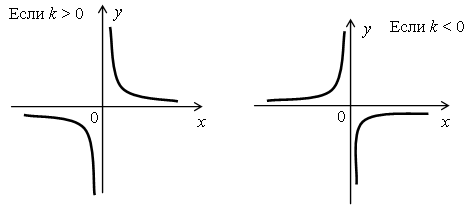
После этого полезно сделать вывод о расположении гиперболы в зависимости от коэффициента k, то есть выполнить № 192. После его выполнения желательно, чтобы обучающиеся занесли в тетрадь следующую иллюстрацию:
Функция y =
График - гипербола
№ 257 (а, д).
Р е ш е н и е
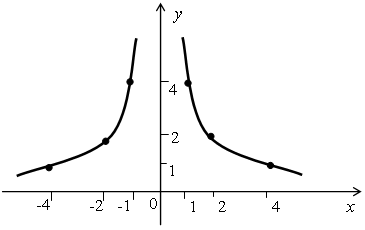
а) Для построения графика функции y = 
необходимо рассмотреть два случая. При х > 0 данная функция
совпадает с функцией y = 
, а при х < 0 - с функцией y = 
. Поэтому получим график:
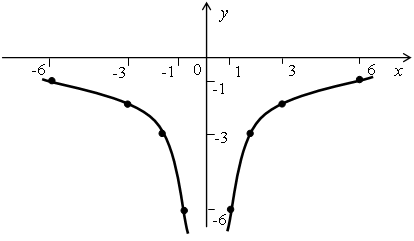
д) y = 
.
Рассуждая аналогично, получим график:
-
Проверочная работа.
В а р и а н т 1
1. Вычислите:
а) 7 · 14-1; б) -5 · 2-3; в) 3-2 + 6-1;
г) 5-1 - 10-1; д) 9 +
; е) 137 - 0,1-2.
2. Представьте в виде дроби:
а) х-1 + у-1; б) ab-2 - a2b; в) (m - n)-3.
В а р и а н т 2
1. Вычислите:
а) 3-2 · 72; б) -2 · 5-3; в) 8-1 + 2-2;
г) 4-1 - 12-1; д) -3 +
; е) 0,01-1 - 165.
2. Представьте в виде дроби:
а) х-2 + у-2; б) х-1у + ху-1; в) (х - у)-2.
-
Формирование умений и навыков.
На этом уроке формироватья умение выполнять преобразования и упрощать выражения, содержащие степень с целым показателем.
1. № 996 - устно, № 997, № 998 (б, г).
Р е ш е н и е
№ 997.
а) а12 = а4 · 3 = (а4)3; б) а12 = а-6 · (-2) = (а-6)-2.
№ 998.
б) х0 : х -5 = х0 - (-5) = х5; б) х6 : х п + 2 = х6 - (п + 2) = х4 - п.
2. № 999, № 1000.
Р е ш е н и е
№ 999.
а) 
;
б) 
;
в) 
;
г) 
;
д) 
;
е) 
.
№ 1000.
а) 
;
при а = -0,125, b = 8 ab = (-0,125) · 8 = -1.
б) 
;
при 
.
3. № 1002, № 1004 (б, г).
Р е ш е н и е
№ 1002.
а) 
;
б) 
;
в) 
;
г) 
;
д) 
;
е) 
.
4. № 1005 (б, г), № 1007 (б, г), № 1008 (б, г).
Перед выполнением этих упражнений следует повторить правило умножения дробей.
Р е ш е н и е
№ 1005.
б) 
;
г) 
.
№ 1007.
б) 
=
;
г) 
.
№ 1008.
б) 
.
г) 
.
5. Сильным в учебе обучающимся предложить для решения задание повышенной трудности.
№ 1009.
Р е ш е н и е
По теореме Виета, 
и 
.
.
Подставляем в уравнение соответствующие значения и получаем:
.
О т в е т: 1.
-
Итоги урока.
Вопросы обучающимся:
- Сформулируйте правила умножения и деления степеней с одинаковым основанием.
- Сформулируйте правила возведения в целую степень произведения и дроби.
- Сформулируйте правило возведения степени в целую степень.
-
Домашнее задание: выполнить № 1001, № 1003, № 1004 (а, в), № 1006, № 1007 (а, в).
.
7