Учителю
Разработка урока по геометрии на тему 'Теорема Пифагора' (8 класс)

Разработка урока по геометрии на тему 'Теорема Пифагора' (8 класс)

Автор публикации: Жунусова Д.М.

Дата публикации: 15.12.2014

Краткое описание: Данный урок направлен на привитие умений учащимся применять знания Теремы Пифагора при решении как стандартных, так и нестандартных задач. Важным в ходе урока является умение учащихся работать с дополнительной литературой: ученики самостоятельно искали другие доказат

предварительный просмотр материала

Геомерия, 8 класс.

Тема урока: Теорема Пифагора.

Тип урока: Закрепление изученного материала.

Цель урока:

Ученики знают теорему Пифагора и умеют ее доказывать;
Ученики умеют применять теорему Пифагора при решении стандартных и нестандартных задач;
Ученики умеют ясно выражать собственные мысли;
Ученики умеют работать самостоятельно с дополнительной литературой;
Ученики умеют самооценивать собственную деятельность.

Воспитание настойчивости и трудолюбия.

КУ учеников:

Я знаю теорему Пифагора и умею ее доказывать;
Я умею применять теорему Пифагора при решении задач.

Метод обучения: наглядный, самостоятельный, групповой.

Оборудование: интерактивная доска, веревка с 2 узлами, иллюстрации к историческим задачам.

ХОД УРОКА.

І. Организационный этап. Постановка цели урока.

Деятельность учителя

Деятельность учащихся

Сообщает тему и цели урока.

Ученики формулируют критерии успешности урока.

Приводит схему построения урока:

Исторические сведения.
Различные доказательства теоремы Пифагора.
Решение задач по готовым чертежам.
Найти ошибку.
Решение исторических задач.
Найдите верные и неверные утверждения.

Читают план урока.

ІІ. Исторические сведения.

На слайде портрет Пифагора:

Кто изображен на слайде и что можете о нем рассказать?

Отвечают на вопрос учителя:

В Древней Греции жил ученый Пифагор (род. ок. 580 г. до н.э., а умер в 500 г. до н.э.). О жизни этого ученого известно немного, зато с его именем связано много легенд. Рассказывают, что он много путешествовал, был в Египте, Вавилоне, Индии изучал древнюю культуру и достижения науки разных стран. Вернувшись на родину, Пифагор организовал кружок молодежи из представителей аристократии. В кружок принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учение основателя. Так на юге Италии возникла пифагорейская школа. Пифагорейцы занимались математикой, философией, естественными науками. Ими было сделано много важнейших открытий в арифметике и геометрии. В школе существовал обычай, по которому авторство всех математических работ приписывалось Пифагору. Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили имя своего учителя множеством легенд. Поэтому установить правду о Пифагоре невозможно.

ІІІ. Различные доказательства теоремы Пифагора.

Предлагает ученикам сформулировать и доказать теорему Пифагора.

Ученик формулирует и доказывает теорему Пифагора.

Ученик оценивает свой ответ.

ІV. Решение задач по готовым чертежам.

В это время учитель раздает ученикам наборы задач с готовыми чертежами.

Остальные учащиеся решают задачи, ответы проверяют по ключу и выставляют самооценки. (За каждый правильный ответ - 1 балл)

ІІІ. Различные доказательства теоремы Пифагора.

В настоящее время имеется более ста различных доказательств теоремы Пифагора. На прошлом уроке я просила вас найти другие доказательства теоремы.

Ученики формулируют и приводят другие доказательства теоремы Пифагора, отличные от учебника.

Ученики оценивают свои ответы.

V. Найти ошибки и закончить решеине.

На слайде задачи и начала решений. Предлагает ученика найти ошибки и закончить решения.

Задача 1. Одна из диагоналей параллелограмма является его высотой. Найдите эту диагональ, если периметр параллелограмма равен 50 см, а разность смежных сторон - 1 см.

Дано.

ABCD - параллелограмм

BD┴AD

P_ABCD = 50 см

AB - CD = 1 см

Найти BD

Решение.

ΔABD - прямоугольный, где .ADB = 90°, соответственно AD и BD - катеты, AB - гипотенуза.

По теореме Пифагора BD² = AD² + AB². Для того чтобы найти AD и AB решим систему уравнений

Задача 2. Основания равнобедренной трапеции равны 11 и 23 дм, а боковая сторона - 10 дм. Вычислите высоту трапеции.

Дано.

ABCD - трапеция

AB = CD = 10 дм

BC = 11 дм

AD = 23 дм

BЕ┴AD

Найти BЕ

Решение.

ΔABЕ - прямоугольный, где .ADЕ = 90°, соответственно AЕ и BЕ - катеты, AB - гипотенуза.

По теореме Пифагора АЕ² = ВЕ² + AB². AЕ = AD - BC.

Ученики должны найти ошибки и закончить решения.

AB²= AD² + BD²

BD² = AB² - AD²

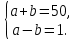
a = 13

b = 12

BD² = 13² - 12²

BD = 5 см

Ответ: BD = 5 см.

AB² = ВЕ² + АЕ²,

AЕ = (AD - BC)/2

AЕ =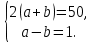 = 6

AB² = ВЕ² + АЕ²,

ВЕ² = AB² - АЕ²

ВЕ² = 10² - 6²

ВЕ = 8 см.

Ответ: BЕ = 8 см.

Ученики оценивают свою работу.

V. Групповая работа. Решение исторических задач.

Задача индийского математика ХII в. Бхаскары, записанная в стихотворной форме (раздает иллюстрации к задаче).

«На берегу реки рос тополь одинокий. Вдруг порыв ветра его ствол надломил. Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки. Осталось три фута всего от ствола. Прошу тебя, скоро мне скажи: У тополя как велика высота?».

Землемеры Древнего Египта для построения прямого угла использовали бечевку, разделенную узлами на 12 равных частей. Покажите, как они это делали.

Указание. В углах должны были узлы.

Ученики в группе совместно ищут решение задачи.

А D

Дано.

ΔACD - прямоугольный

AC = 3 фута

AD = 4 фута

Найти AВ

Решение.

AВ = AС + CD, ВС = CD

По теореме Пифагора CD² = AС² + AD²

CD² = 3² + 4², CD² = 25, CD = 5 (Ф)

AВ = 3 + 5 = 8 (Ф).

1 фут (1 Ф) ≈ 30,5 см.

Ответ: 8 футов или ≈ 244 см.

Пытаются с помощью веревки с узлами построить прямой угол.

Ученики оценивают работу друг друга.

VI. Задание на дом.

Учитель дает домашнее задание № 158,160.

Подводит итоги урока:

Назовите, верно ли утверждение:

Любой катет прямоугольного треугольника больше гипотенузы.
Сумма острых углов треугольника больше 90°.
Косинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Произведение котангенса и тангенса острого угла больше 1.
Катет, лежащий против угла в 30°, равен половине гипотенузы.

Ученики записывают домашнее задание.

Ученики определяют истинно или ложно утверждение.

VII. Оценивание и комментирование оценок учащихся.

№

Этапы урока

Самооценка

Взаимооценка

Исторические сведения.

Различные доказательства теоремы Пифагора.

Решение задач по готовым чертежам.

Найти ошибку.

Решение исторических задач.

Найдите верные и неверные утверждения.

ИТОГО

Приложение 1.

ЛИСТ ОЦЕНИВАНИЯ

ФИ учащегося_____________________________________________

№

Этапы урока

Самооценка

Взаимооценка

Исторические сведения.

Различные доказательства теоремы Пифагора.

Решение задач по готовым чертежам.

Найти ошибку.

Решение исторических задач.

Найдите верные и неверные утверждения.

ИТОГО

---------------------------------------------------------------------------------------------------------------------

Используемая литература.

Остренкова Г.//Математика, 2005 г., №4, стр. 13-15.

⇧

⇩