Тема: «Решение линейных уравнений и неравенств с параметрами»

Цель: Повторить, закрепить и привести в систему знания и умения решать линейные уравнения и неравенства с параметрами, полученные в 9 классе;

Развивать логическое мышление, математическую речь, интерес к изучению математики;

Воспитывать аккуратность, взаимопонимание.

Формы работы: фронтальная беседа, .

Метод работы: Методы организации учебно-познавательной деятельности: наглядные, практические, исследовательские.

Методы стимулирования и мотивации учебно-познавательной деятельности: учебная дискуссия, эмоциональное воздействие.

Методы контроля: письменный, самопроверка.

Оборудование:

интерактивная доска

Литература: Алгебра и математический анализ. Учебник. 10 класс Виленкин Н. Я. - изд. Мнемозина, 2006 г.

Ход урока

Оргмомент

Актуализация знаний

Обычно в уравнении или неравенстве буквами обозначаются переменные. Решить уравнение или неравенство - означает найти множество значений неизвестных, удовлетворяющих этому уравнению или неравенству. Иногда уравнения или неравенства, кроме букв, обозначающих неизвестные, содержат другие буквы, называемые параметрами. Предавая параметрам разные числовые значения, получаем различные уравнения или неравенства. Например, в линейном уравнении ах+b=0 или неравенстве ах+b>0, x - переменная, a, b- параметры.

При решении уравнений или неравенств надо сначала найти множество допустимых значений параметров, а затем разбить это множество на части, в каждом из которых ответ выражается функцией через параметры.

О₁. Множество значений параметра, при каждом из которых f(a,x) или существуют в области действительных чисел, называют областью допустимых значений параметра а.(слайд2)

Пр₁ .

Данное соотношение имеет смысл при .

Пр₂ - имеет смысл при a≥3

О₂ Число х₀ называют допустимым значением переменной х, если числа f(a, x₀) и действительны при каждом допустимом значении параметра.

О₃ Областью определения неравенства (уравнения) множества всех допустимых значений х, при которых уравнение (неравенство) имеет смысл.

Пр₁:

Пр₂: хR

Вспомним решение линейных уравнений и неравенств с параметрами a, b.

ax=b

xR

1. Если a≠0, b Є R, то х=b/a - единственный корень.

2. Если а=0, b=0, то 0х=0, уравнение имеет множество корней.

3. Если a=0, b≠0, то 0x=и уравнение корней не имеет.

ax

xR

1. Если a=0, b Є R, то 0x<b. Если b>0, то неравенство имеет множество решений. Если b<0, то неравенство решений не имеет.

2. Если a<0, b≠0, то x>b/a.

3. Если a>0, b≠0, то x

Закрепление теоретических навыков

Рассмотрим решение линейных уравнений и неравенств.

1. 3(2а - х)=ах+1

а Є R, х Є R.

6а-3х=ах+1

-3х-ах=1-6а

х(3+а)=6а-1

а) а=-3, уравнение корней не имеет;

б) а≠-3, то х =

Ответ: а) а=-3, уравнение корней не имеет;

б) а≠-3, то х =

2. 3(2а - х) < ах+1

а Є R, х Є R.

х(3+а) > 6а-1

а) а=-3, то 0х > -19, неравенство имеет множество решений;

б) а > -3, то х > ;

в) а < -3, то х < ;

Для самостоятельного решения с последующей проверкой ответов.

1. ах-3 =х+2. Ответ : а=1, нет корней; а≠1, х=.

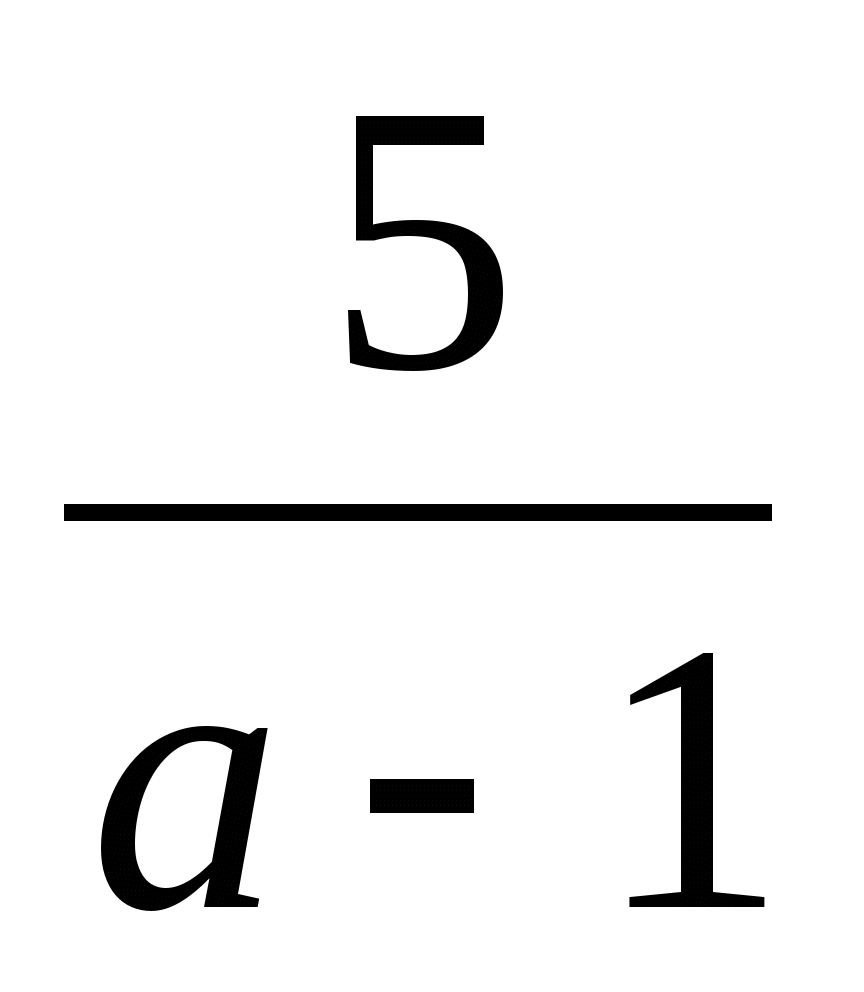2. ах-3 > х+2. Ответ : а=1, нет решений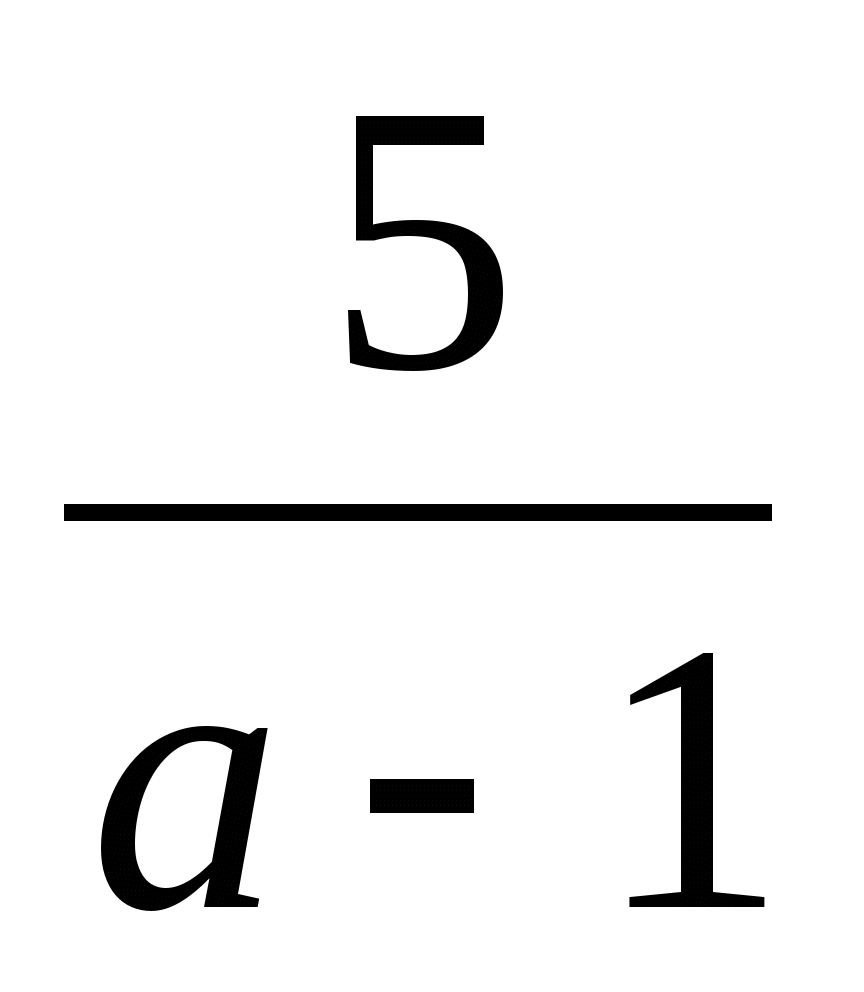; а>1, х>; а<1, х<.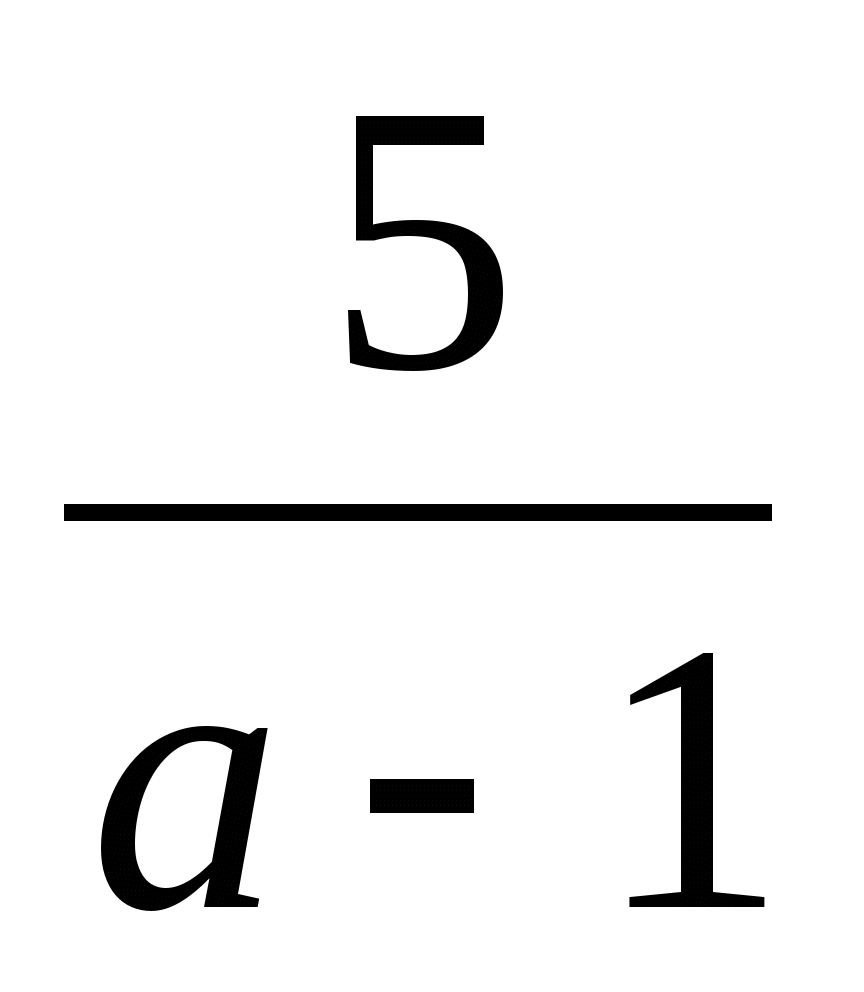

И следовательская деятельность

Решите уравнение с параметром:

а=1, уравнение корней не имеет;

а≠1; 3(а+2)х -2(а-1)=(2х-1)(3а-3)

х(12-3а)=1-а

а) а=4, то 0х=-3, уравнение корней не имеет;

б) а≠4, то х =.

Ответ: а=1, а=4, уравнение корней не имеет;

а≠1, а≠4, то х =.

Рассмотрим неравенство с параметром:

а) при а=1 неравенство смысла не имеет;

б) при а=4 неравенство решений не имеет;

в) если а-1>0, т.е. а>1

3(4-a)x+(a-1)<0

3(4-a)x<(a-1)

а) 1<a<4, то х <;

б) a>4, то х >.

г) если а-1<0, т.е. а<1

3(4-a)x+(a-1)>0

3(4-a)x>(a-1)

а) a<1, а>4, то х >;

б) aЄǾ не имеет смысла.

Ответ: 1) а=1, а=4 неравенство смысла не имеет;

2) 1то х <;</</span>

3) a<1, а>4, то х >.

Задания для самостоятельного решения:

Итог

На следующем занятии мы будем рассматривать решение квадратных уравнений и неравенств с параметрами, поэтому вспомните решение квадратных уравнений.

Домашнее задание

1. (а+6)х - 8х + а=0;

2.