Тема урока Выполнение действий над действительными числами. Степень с целым показателем и ее свойства. Тождественные преобразования рациональных выражений.».

, ГУ « Средняя общеобразовательная школа №5» отдела образования акимата г. Костаная

ПЛАН-КОСПЕКТ УРОКА

ФИО (полностью) Пластун Сергей Владимирович

Предмет алгебра

Класс 9А, 9Б-1, 9Б-2, 9В

Дата 04.05.16

Источники

Базовый учебникОҚУЛЫҚ: АЛГЕБРА, АЛМАТЫ «МЕКТЕП», 2013

Авторлары: Абылкасымова А.Е., Корчевский В.Е., Жумагулова З.А.

УЧЕБНИК:АЛГЕБРА, АЛМАТЫ «МЕКТЕП», 2013

Авторы: Абылкасымова А.Е., Корчевский В.Е., Жумагулова З.А.

Дополнительная литература ОҚУЛЫҚ: АЛГЕБРА, ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ, АЛМАТЫ «МЕКТЕП», 2013

Авторлары:Шыныбеков А.Н.

УЧЕБНИК: АЛГЕБРА, ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ, АЛМАТЫ «МЕКТЕП», 2013

Авторы:Шыныбеков А.Н.

Тема урока: Выполнение действий над действительными числами. Степень с целым показателем и ее свойства. Тождественные преобразования рациональных выражений.».

Цели урока: повторение темы, обобщение темы, подготовка к итоговой аттестации в 9 классе. Написать краткий конспект, в котором содержатся все основные понятия и утверждения заданной темы, провести отбор основных сведений, обобщить полученные знания по теме.

Подготовка к уроку: урок проходит после изучения главы «Алгебраические дроби». Составление схемы-конспекта - это обобщение всего ранее изученного теоретического материала, записанного в удобной форме для зачета по теме.

Класс разбит на четыре группы (I группа - слабая подготовка учащихся; II и IV группы - среднего уровня подготовки; III группа - более высокий уровень подготовки).

Рассматривается 6 тем:

1. Основные понятия алгебраической дроби;

2. Основное свойство алгебраической дроби;

3. Сложение и вычитание дробей с одинаковыми знаменателями;

4. Сложение и вычитание дробей с разными знаменателями;

5. Умножение, деление, возведение в степень дробей;

6. Преобразование выражений.

Воспитательные:

• Развитие самостоятельности.

• Способствовать формированию у учащихся чувства коллективизма, ответственности за общее дело в ходе групповой работы.

Тип урока: повторение материала

СТРУКТУРА И ХОД УРОКА

Этап урока

Деятельность учителя

(например,

иллюстрация, демонстрация и т. д.)

Деятельность ученика

Время

(в мин.)

1

2

3

4

5

1

Организационный момент

1 мин

2

Мотивационное начало урока.

Вводная беседа

2 мин

3

Проверка домашнего задания

2 мин

4

Повторение пройденного материала

Работа в тетрадях

33 мин

5

Физ. минутка

2 мин

6

Первичный контроль

0 мин

7

Подведение итогов, постановка домашнего задания

5 мин

Ход урока:

1. Организационный момент. Взаимное приветствие учителя и учащихся. Определение отсутствующих, проверка подготовленности учащихся к уроку, организация внимания учащихся

2. Проверка домашнего задания: Выявления уровня знаний учащимися заданного на дом материала; определение типичных недостатков в знаниях и причин их появления; ликвидация обнаруженных недочетов.

3. Всесторонняя проверка знаний: Стимулировать опрашиваемых и весь класс к овладения рациональными приемами умения и самообразования

4. Постановка цели: Подготовка учащихся к активному и сознательному усвоению знаний. Сообщение темы, цели и задачи изученного материала. Постановка перед учащимися цели урока.

1. Организационный момент и проверка домашнего задания (тетради сдаются учителю на оценку и получают вторые тетради).

2. Повторение темы «Выполнение действий над действительными числами. Степень с целым показателем и ее свойства. Тождественные преобразования рациональных выражений.».

Весь класс заполняет блок схему.Тема: Алгебраические дроби

Определение:- алгебраическая дробь, где числитель дроби P(a,b), а знаменатель дроби Q(a,b).

P(a,b) и Q(a,b) - многочлены от переменных a, b, которые принимают лишь допустимые значения, т.е. такие, что Q(a,b)

Основное свойство дроби

M

M

Используется при приведении к общему знаменателю.

Используется при сокращении дробей.

Правила изменения знака

а)

б)

Действия с дробями

рациональное уравнение, где P(x) и Q(x) - многочлены.

Решение рациональных уравнений:

Пусть P(a,b), Q(a,b), C(a,b), D(a,b) - многочлены.

- рациональное выражение, где - дробное выражение. С - целое выражение.

3. Решение практических задач с использованием блок - схемы.

1 Сократите дроби:

а)

б) .

2 Найдите значение выражения:

при х = -2.

=, если х = -2, то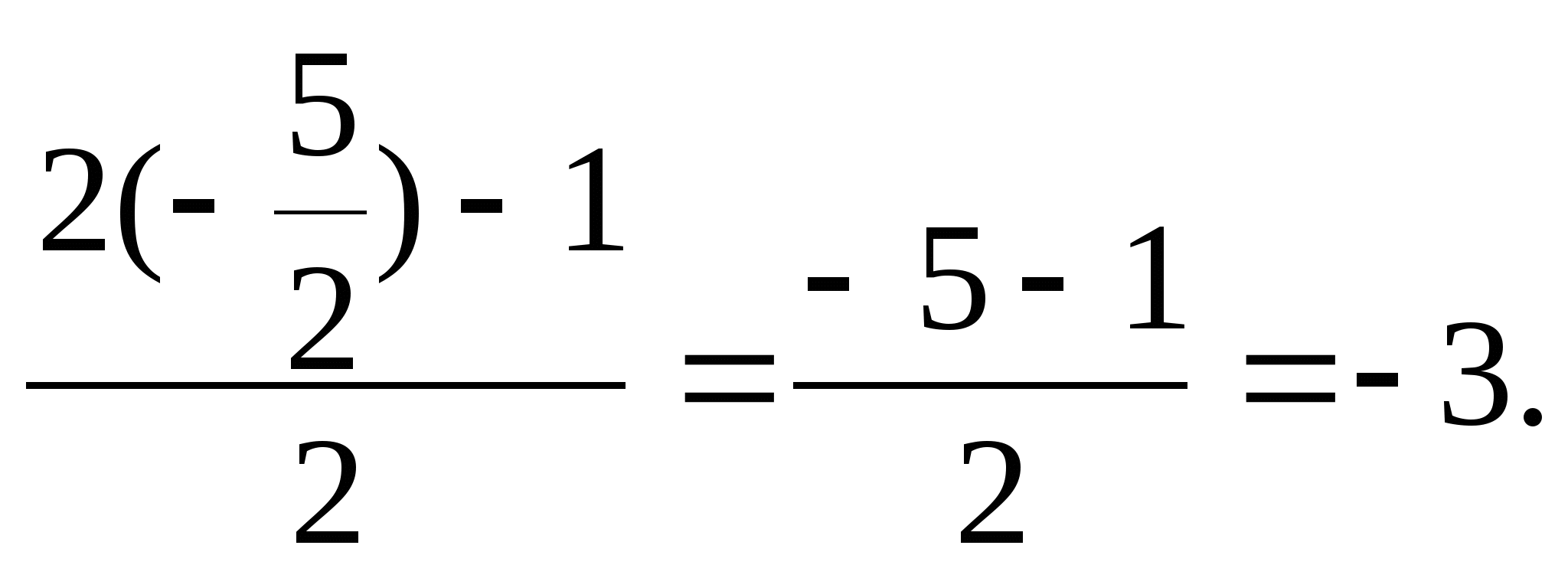

3 Укажите допустимые значения переменной m:

Область допустимых значений:

2m+9

2m

m.

4 Представьте в виде дроби выражения:

а) ;

б) .

5 Упростите выражения:

а) ;

б) .

6 Представьте в виде дроби:

а) ;

б) .

7 Упростите выражения:

а) ;

б) mx.

8 Упростите выражения:

а)

=.

в) .

4. Работа по группам.

III группа - работает самостоятельно по карточкам на оценку (по четырем темам).

1 Сократите дроби:

а) ; б) .

2 Представьте в виде дроби выражения:

а) ; б) .

3 Упростите выражения:

а) ; б) .

4 Выполните действия:

а) ; б) .

I группа - работает с учителем у доски.

1 Сократите дробь:

а) ; б) .

2 Представьте в виде дроби выражения:

а) ; б) .

3 Представьте в виде дроби:

а) ; б) .

4 Упростите выражения:

а) ; б) .

II группа - работают по одному представителю у доски, консультируясь с учителем.

1 Сократите дробь:

а) ; б) .

2 Представьте в виде дроби выражения:

а) ; б) .

3 Представьте в виде дроби:

а) ; б) .

4 Упростите выражения:

а) ; б) .

IV группа.

1 Сократите дробь:

а) ; б) .

2 Представьте в виде дроби выражения:

а) ; б) .

3 Представьте в виде дроби:

а) ; б) .

4 Выполните действия:

а) ; б) .

В конце первого урока 10 человек проходят тестирование через Мобильный класс, Остальные работают с учителем или делают дополнительные задания. Затем следующие 10 человек. Тестирование проводится с использованием тестов ,которые находятся на диске , в конце каждой темы.

5. Домашнее задание.

I группа

1 Придумайте примеры алгебраических дробей, которые имели бы смысл при:

а) х; б) у

2 Найдите значение алгебраической дроби:

а) , при с= -2, d=1; б) , при х=3, у=4.

3 Сократите дробь:

а) ; б) .

4 Приведите к новому знаменателю:

а) ; б) .

5 Выполните действия:

а) ; б) .

6 Упростите выражения:

а) ; б) -.

7 Выполните действия:

а) ; б) .

II и IV группы.

1 Докажите, что при любых значениях переменной:

а) значение дроби отрицательное.

б) значение дроби неотрицательное.

2 При каких значениях переменой не имеет смысла алгебраическая дробь:

а) ; б) .

3 Привести дроби к общему знаменателю:

а) ; б) .

4 Вычислите:

а) ; б) .

5 Упростите выражения:

а) ; б) .

6 Упростите выражения:

а) ; б) .

7 Выполните действия:

а) ; б) .

8 Упростите выражения:

а) ; б) .

III группа.

1 Найдите значение дроби:

а) , если ; б) , если .

2 Найдите значение выражения:

а) , если ; б) , если а+2b=7b/

3 Найдите значение дроби:

а) , х=0,5; у=0,25; б) , а= -2,4; b=0,2.

4 Найдите значение выражения:

а) , при а=3; б) , при а=4,5.

5 Вместо «*» запишите такие выражения, чтобы получились верные равенства:

а) ; б) .

6 Выполнить действия:

а) 1-; б) .

Устно повторить тему: «Арифметический квадратный корень и его свойства».

6. Дополнительное задание.

10 баллов.

20 баллов.

30 баллов.

а) Существует ли такое значение d, при котором разность дробей равна 1?

б) Докажите, что значение выражения не зависит от значений входящих в него переменных.