Контрольно измерительные материалы для учащихся 9 класса по алгебре

ЧАСТНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ОРГАНИЗАЦИЯ

«школа АЗЪ БУКИ ВЕДИ»

«Рассмотрено»

Председатель МО

___________Устинова Ю.Д. Протокол № 1 от «____»_________2016 г

«Согласовано»

Заместитель директора по УВР

_____________Безнищенко Е.Н. «____»__________2016 г.

«Утверждено»

Директор

________Чаркина Е.Г.

Приказ № _____ от

«____»_______2016 г.

РАБОЧАЯ ПРОГРАММА

ПО МАТЕМАТИКЕ

9 КЛАСС

БАЗОВЫЙ УРОВЕНЬ

170 ЧАСОВ

(контрольно измерительные материалы)

Составитель: Михайлевская Т.Г.,

учитель математики

высшей квалификационной категории

Симферополь, 2016

Алгебра

Контрольная работа №1 по теме

«Квадратичная функция»

Вариант 1

1. Дана функция f(x) = 1,3 х - 3,9. Найдите f(x) = 0, f(-2), f(10).

2. Разложите на множители квадратный трехчлены:

а) х ² - 12 х + 35;

б) 7у ² + 19у -6.

3. Сократите дробь .

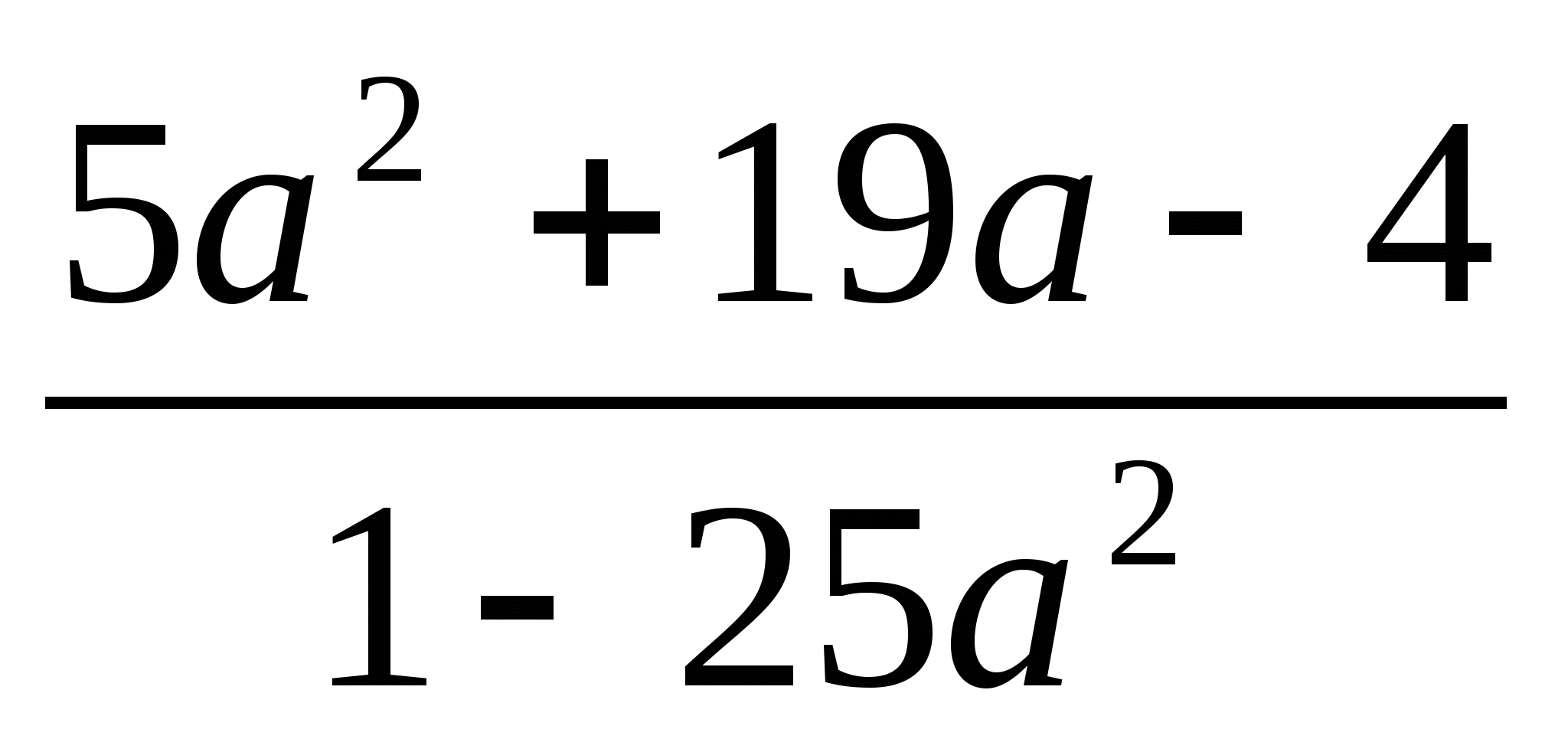4. Найдите область определения функции f(x) = .

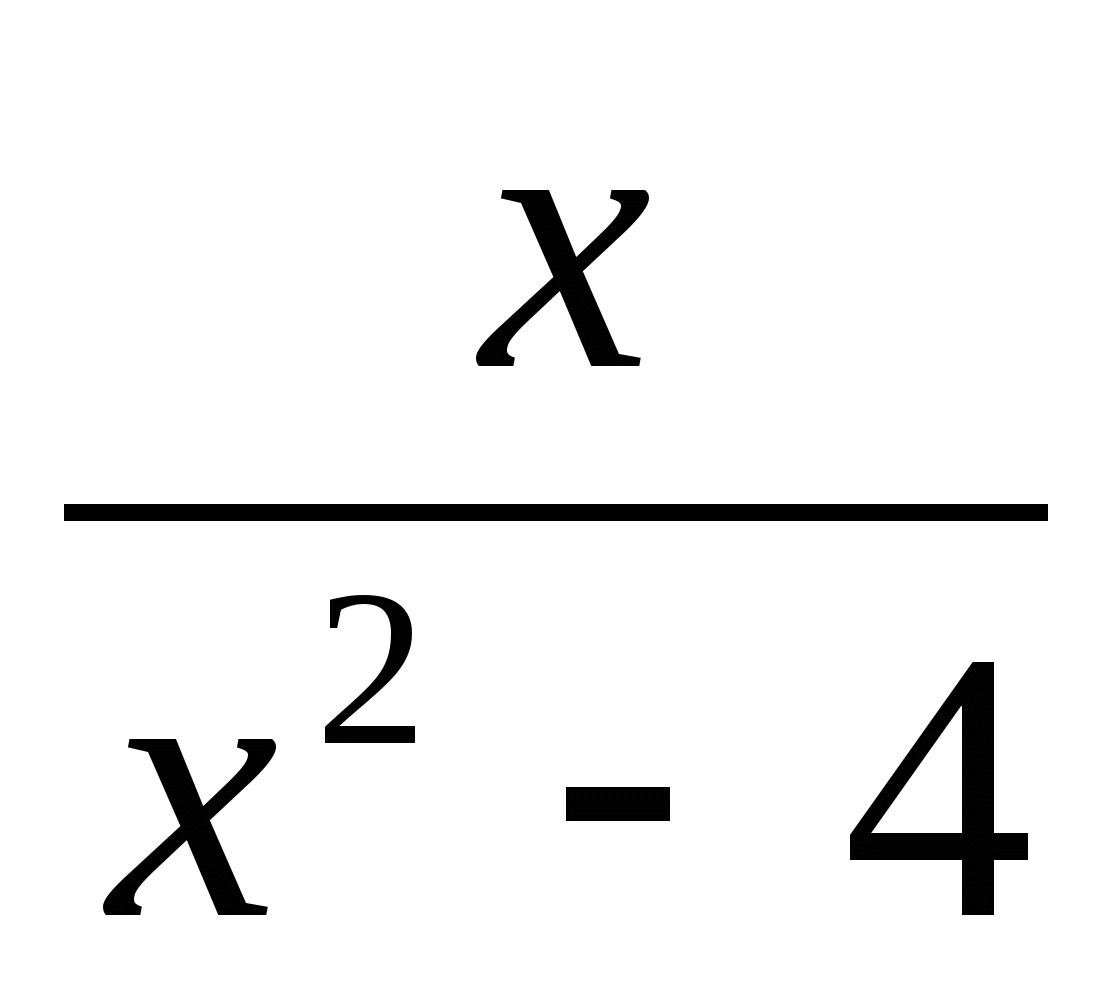5. Найдите область значений функции, промежутки убывания (см. рисунок 1):

6. Найдите наименьшее значение квадратного трехчлена х ² - 8 х + 7.

Вариант 2

1. Дана функция f(x) = 2,4 х - 3,6. Найдите f(x) = 0, f(-3), f(10).

2. Разложите на множители квадратный трехчлены:

а) х ² - 8 х + 15;

б) 7п ² - 3п + 1.

3. Сократите дробь .

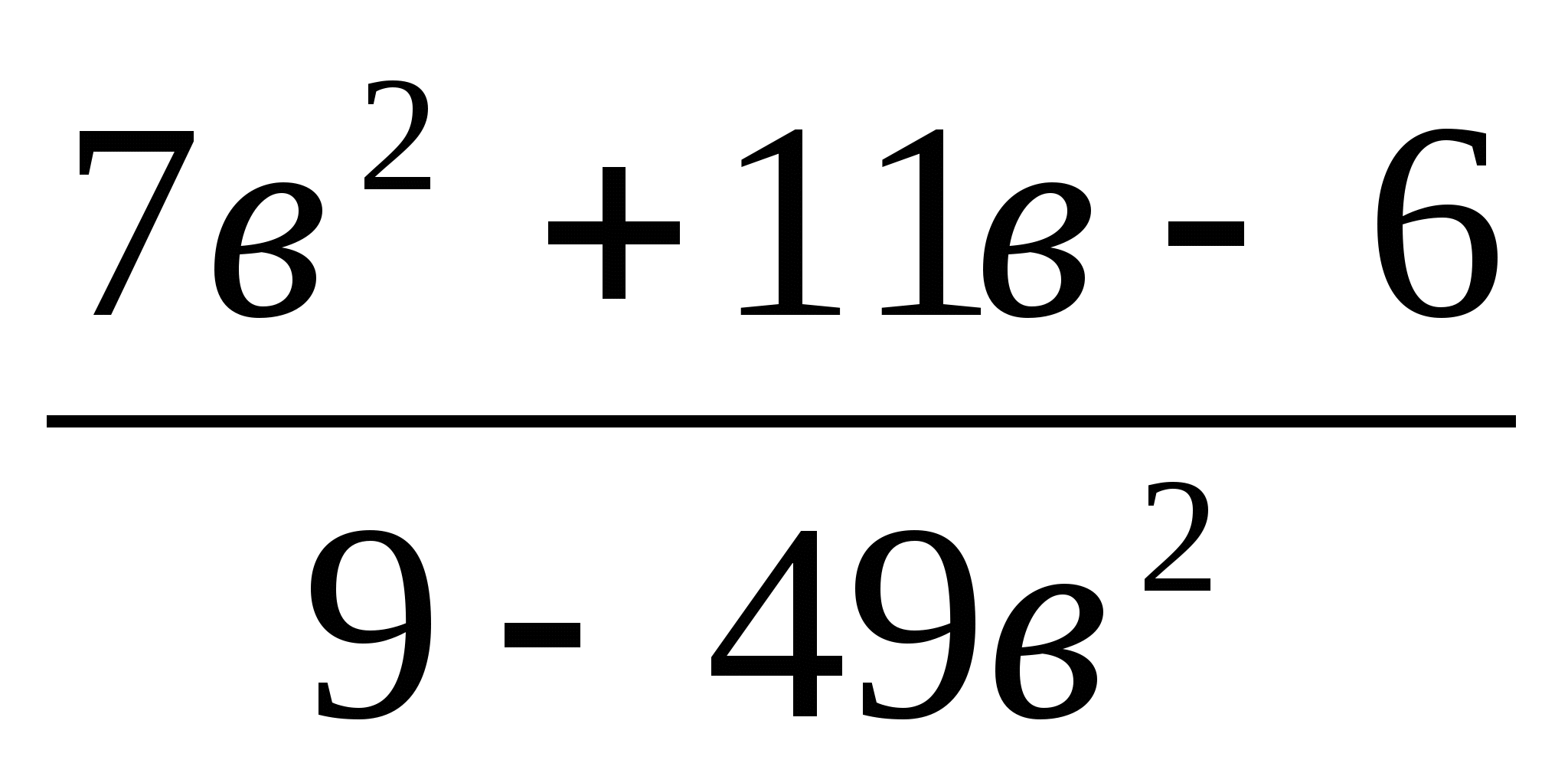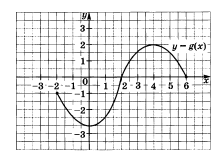
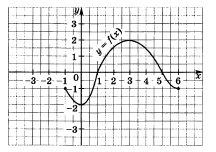
рисунок 1 рисунок 2

4. Найдите область определения функции f(x) = .

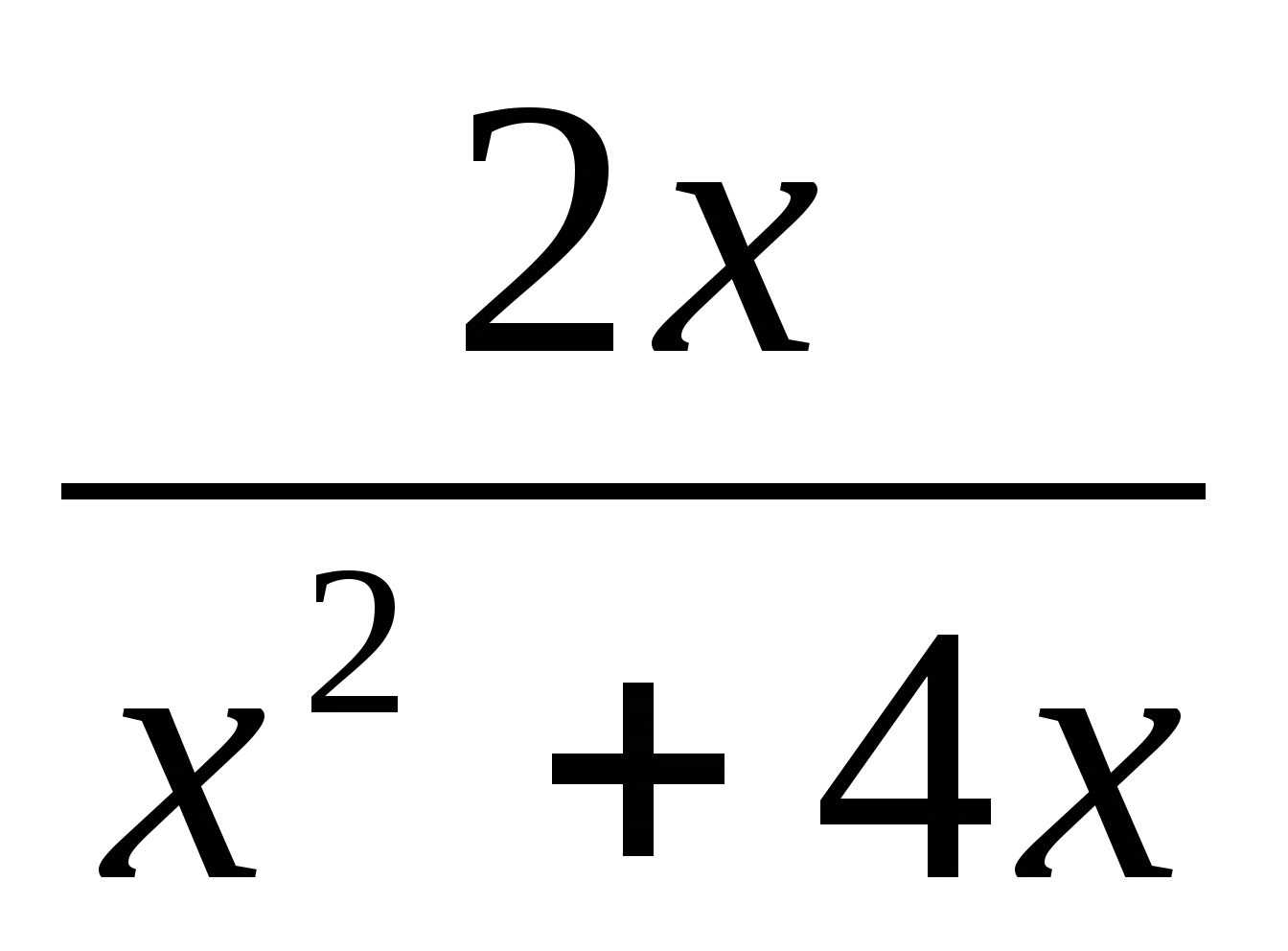5. Найдите область значений функции, промежутки убывания (см. рисунок 2):

6. Найдите наибольшее значение квадратного трехчлена - х ² + 6 х - 4.

Контрольная работа №2 по теме

«Квадратичная функция»

Вариант 1

1. Найдите координаты вершины параболы у = 2х ² - 8 х + 3.

2. Постройте график функции у = х ² - 4 х + 3. Найдите по графику: а) значение у при х = 2; б) значение х, при котором у = 3; в) нули функции; г) промежутки возрастания и убывания функции; д) промежутки, в которых у < 0 и y > 0.

3. Используя шаблон параболы у = х ² , постройте в одной системе координат графики функций : у = - х ² ; у = - х ² +1; у = - (х +1) ² .

4. Параболу у = - 2 х² сдвинули вправо на 2 единицы и вниз на 3 единиц. Задайте формулой функцию, график которой получился в результатах таких преобразований.

5. Не выполняя построения, определите, пересекаются ли парабола у =1/2 х ² и прямая у = 6х - 15. Если точки пересечения существуют, то найдите их координаты.

Вариант 2

1. Найдите координаты вершины параболы у = -х ² + 4 х - 9.

2. Постройте график функции у = х ² + 4 х + 3. Найдите по графику: а) значение у при х = 0,5; б) значение х, при котором у = 3; в) нули функции; г) промежутки возрастания и убывания функции; д) промежутки, в которых у < 0 и y > 0.

3. Используя шаблон параболы у = х ² , постройте в одной системе координат графики функций : у = - х ² - 3; у = (х - 3) ² ; у = - (х - 3) ² .

4. Параболу у = 2 х² сдвинули влево на 3 единицы и вверх на 5 единиц. Задайте формулой функцию, график которой получился в результатах таких преобразований.

5. Не выполняя построения, определите, пересекаются ли парабола у =1/3 х ² и прямая у = 12 - х. Если точки пересечения существуют, то найдите их координаты

Контрольная работа №3 по теме

«Уравнения и неравенства с одной переменной»

Вариант 1

1. Решите неравенство: а) 2 х² - 13х + 6 < 0; б) х² - 9 > 0; в) 3 х² - 6х + 32 > 0.

2. Решите неравенство, используя метод интервалов: а) ( х + 8 )( х - 4 ) > 0; б) .

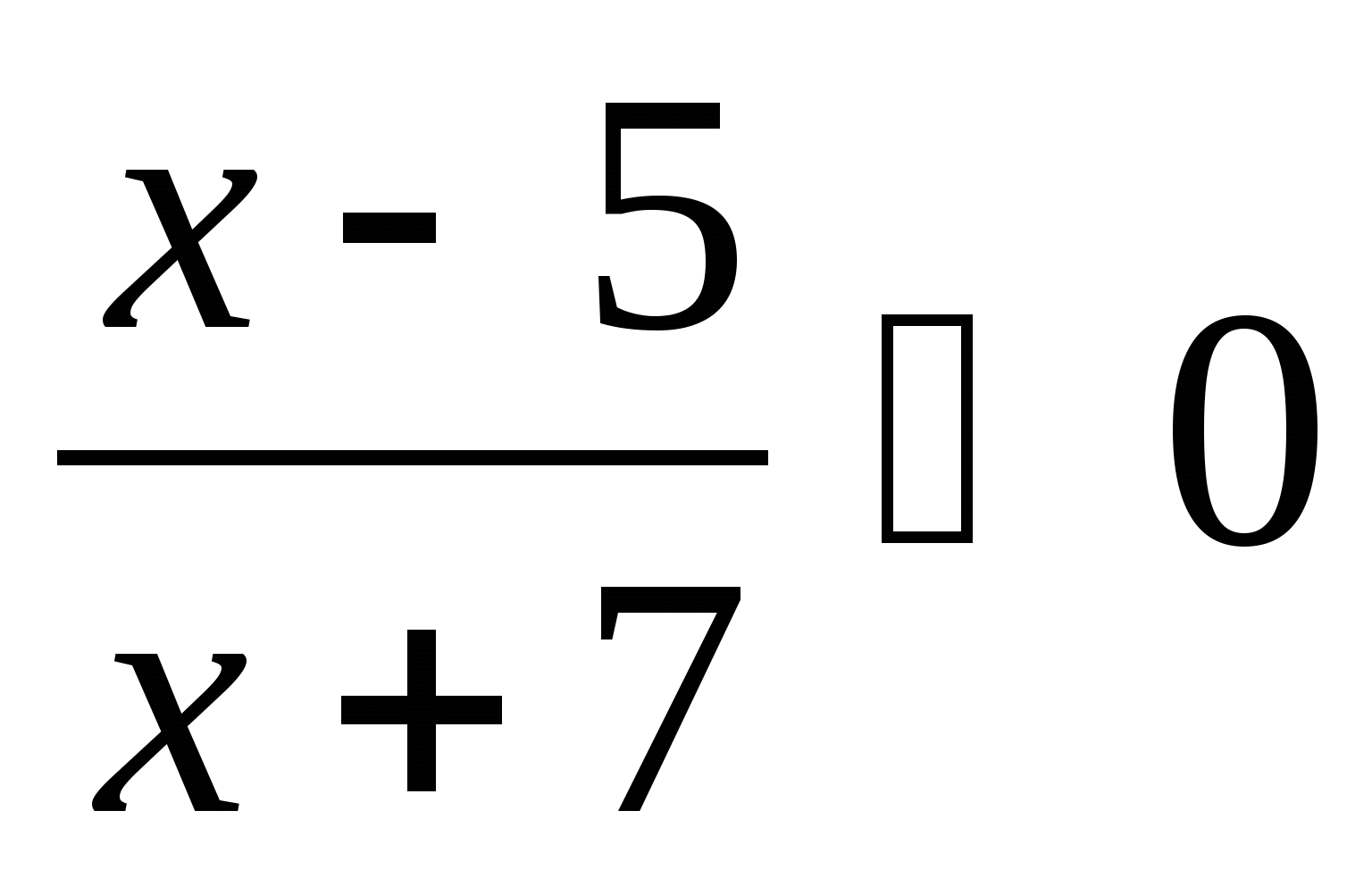3. Решите уравнение: а) х ³ - 81х = 0; б) .

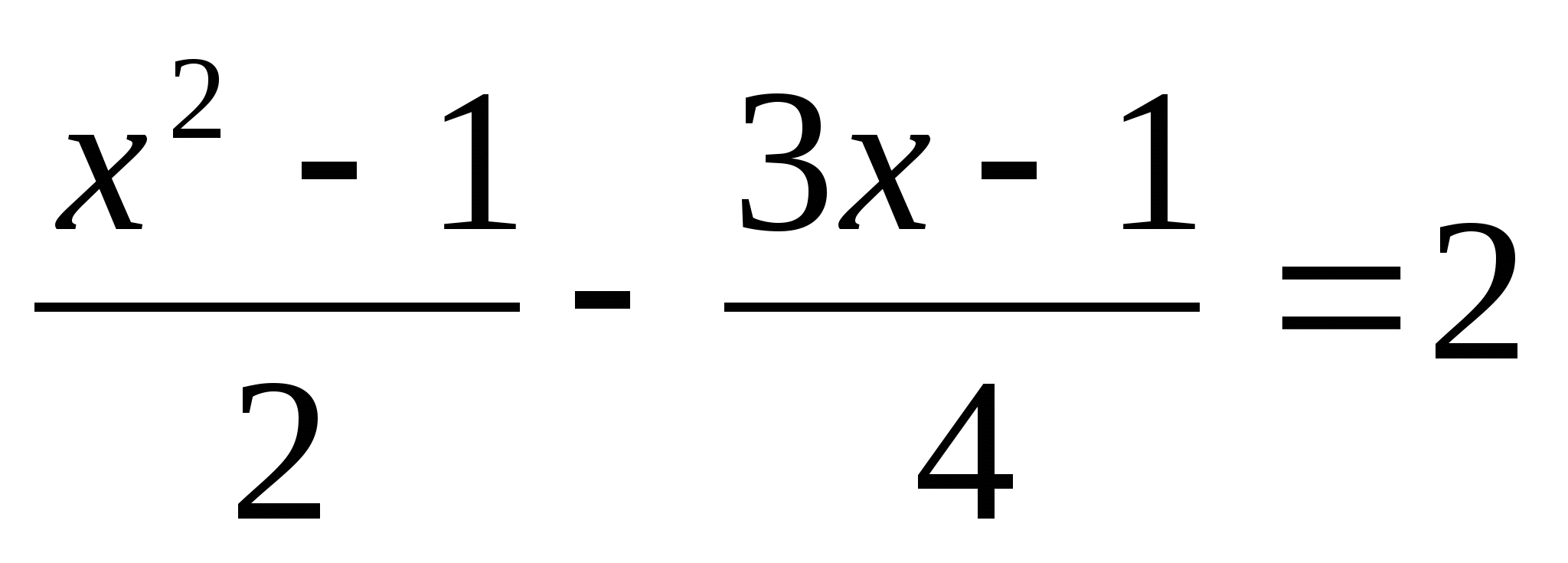4. Решите биквадратное уравнение х ⁴ - 19 х² +48 = 0.

5. При каких значениях t уравнение 3 х² + t х + 3 = 0 имеет два корня?

6. Найдите область определения функции .

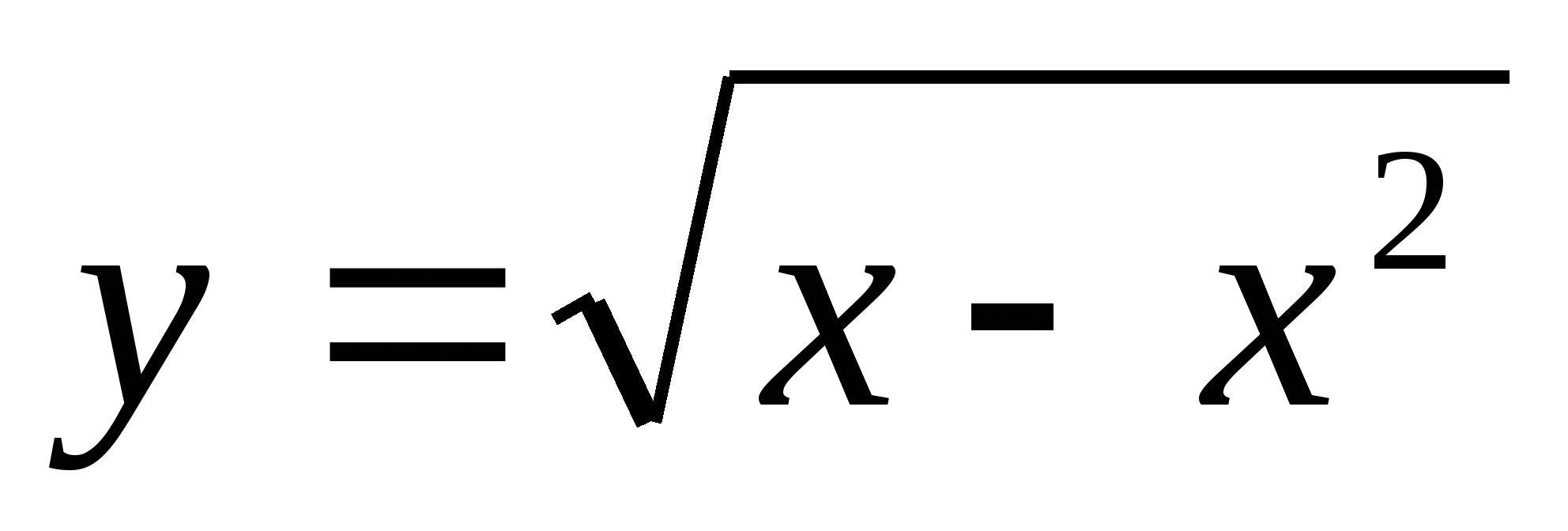Вариант 2

1. Решите неравенство: а) 2 х² - х - 15 > 0; б) х² - 16 < 0; в) х² + 12х + 80 < 0.

2. Решите неравенство, используя метод интервалов: а) ( х + 11 )( х - 9 ) < 0; б) .

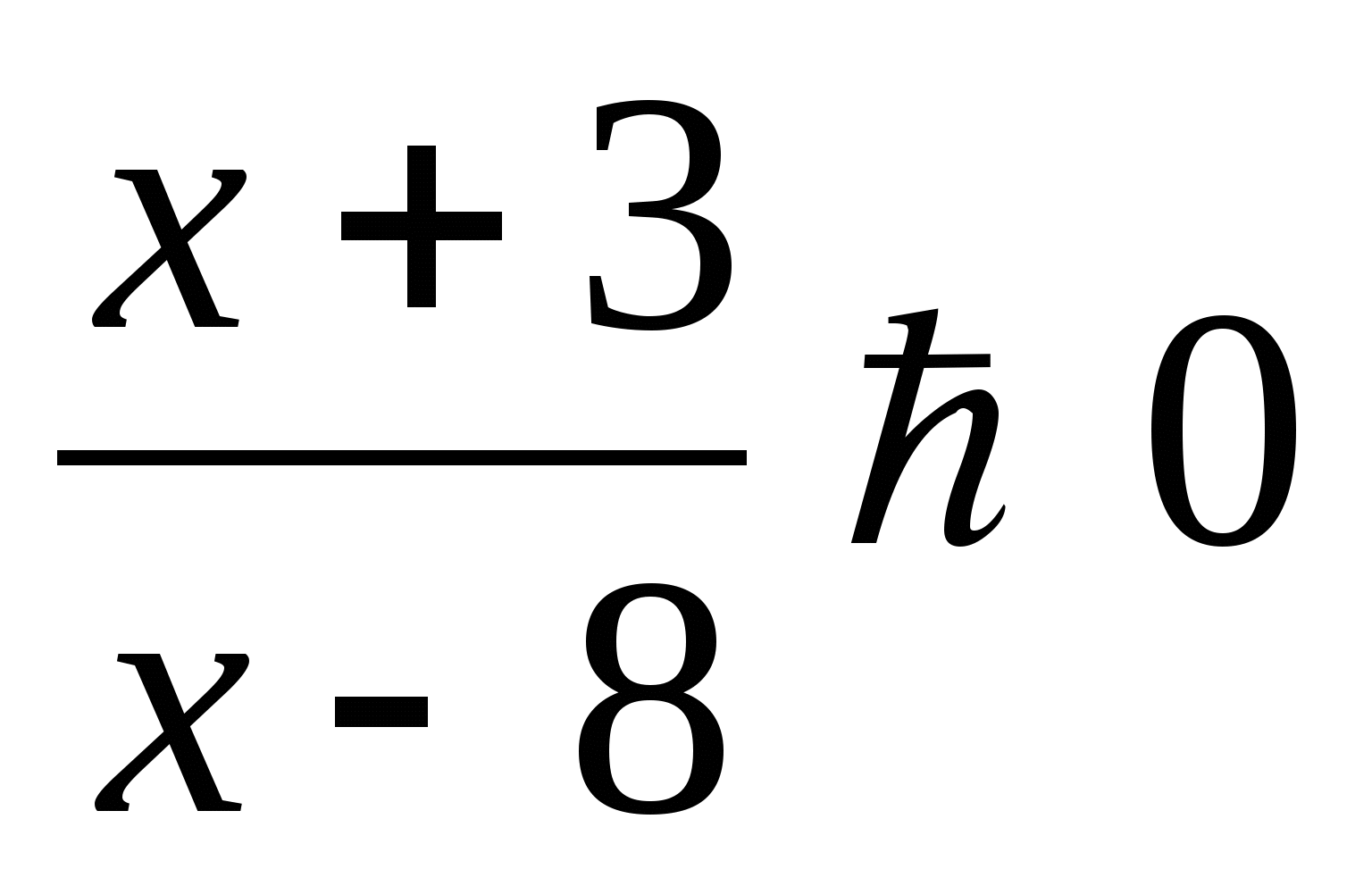3. Решите уравнение: а) х ³ - 25х = 0; б) .

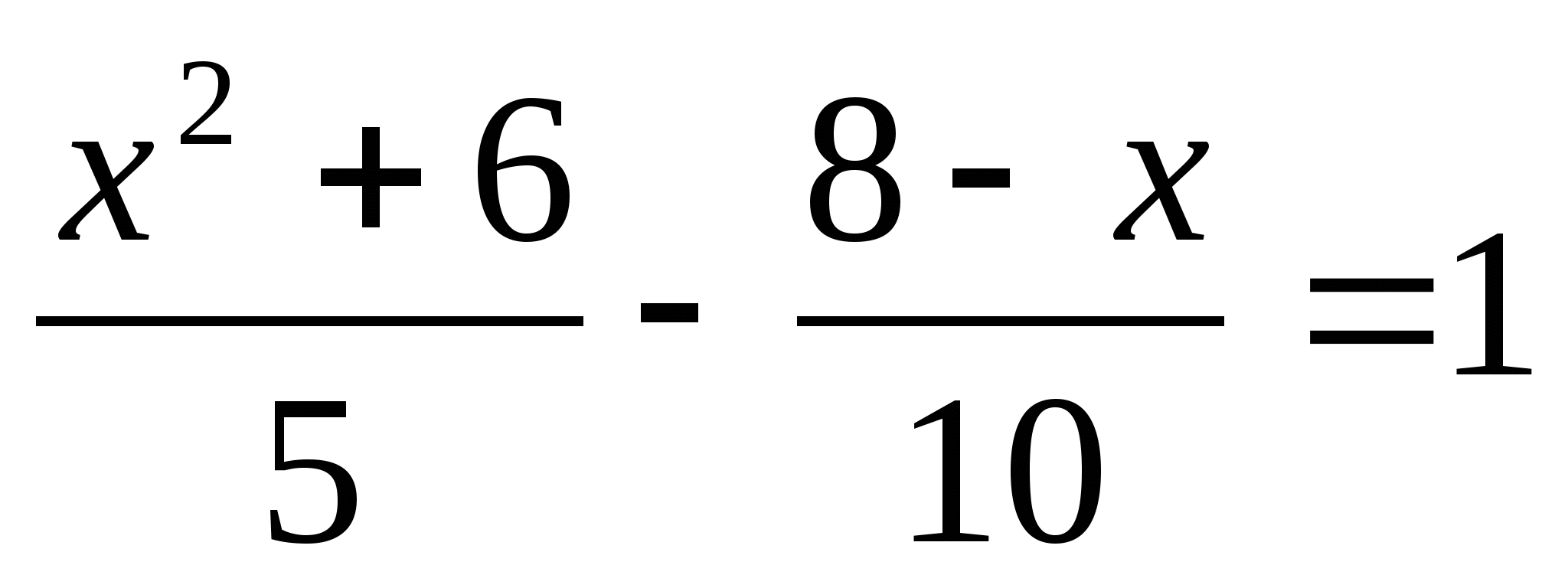4. Решите биквадратное уравнение х ⁴ - 4 х² - 45 = 0.

5. При каких значениях t уравнение 2 х² + t х + 8 = 0 не имеет корней?

6. Найдите область определения функции .

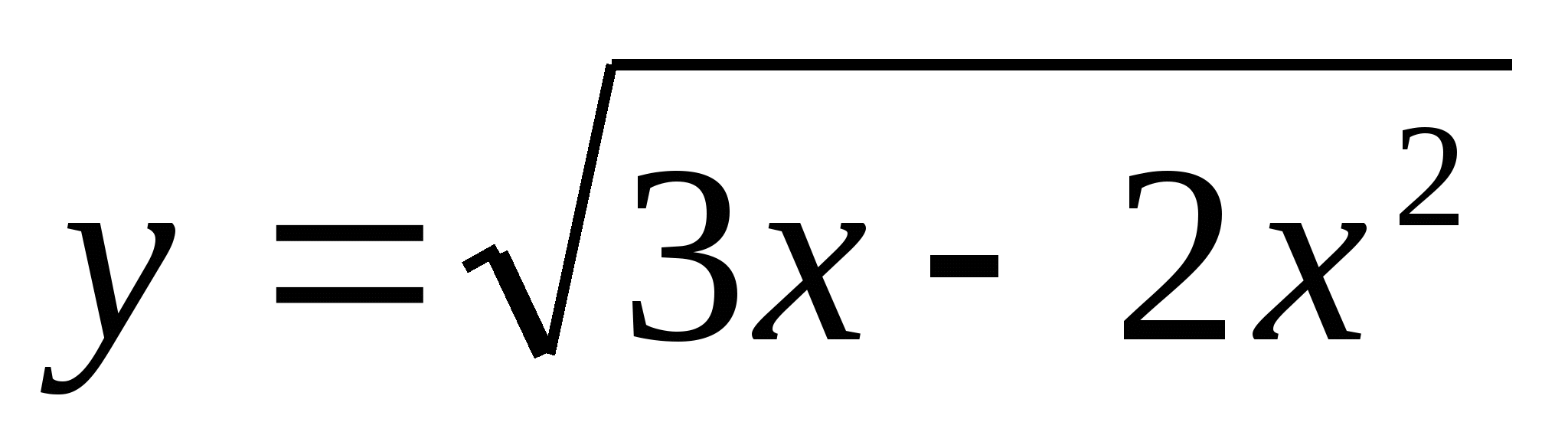Контрольная работа №4 по теме

«Уравнения и неравенства с двумя переменными»

Вариант 1

1. Решите систему уравнений:

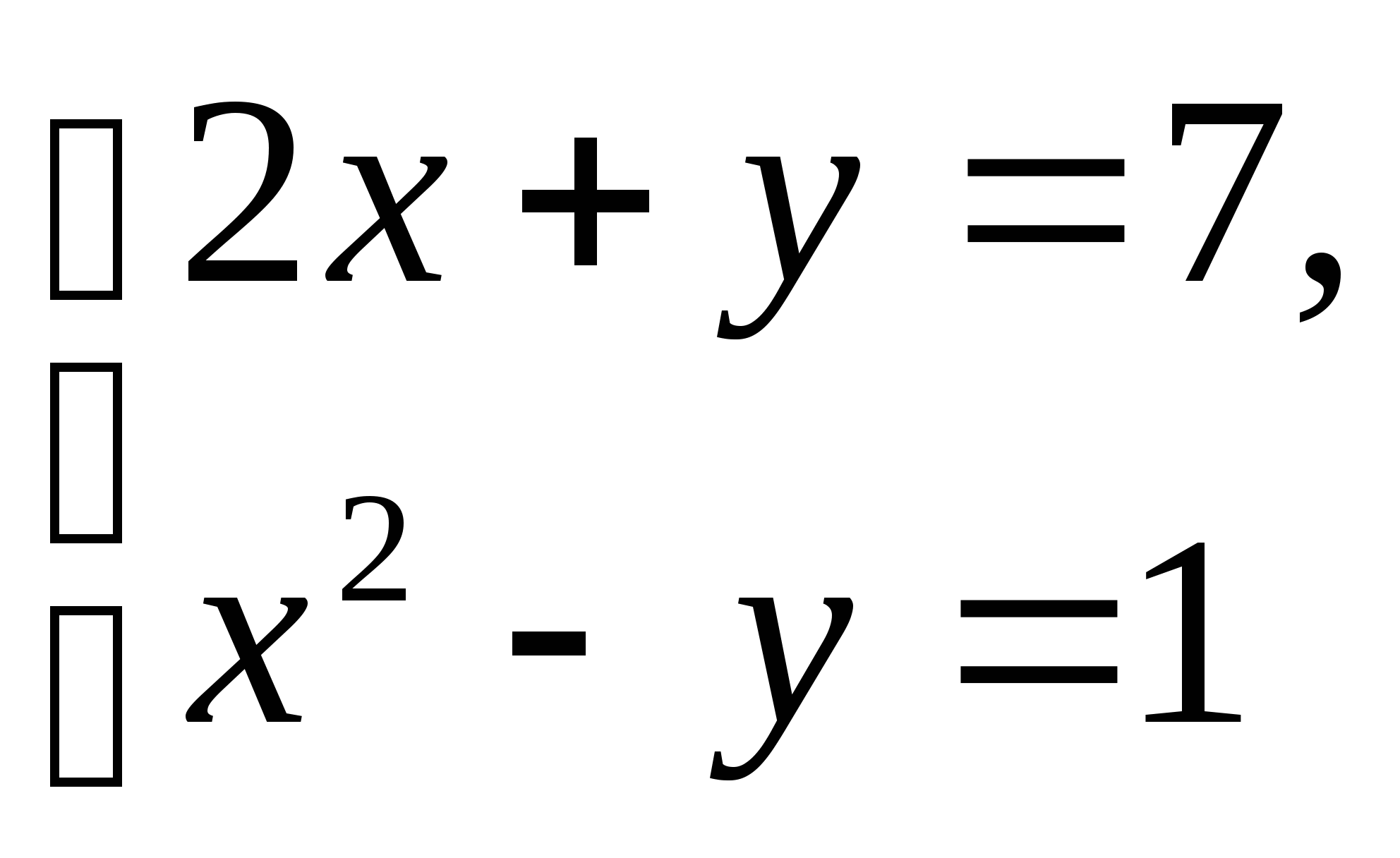
2. Периметр прямоугольника равен 28м, а его площадь равна 40м ² . Найдите стороны прямоугольника.

3. Не выполняя построения, определите, найдите координаты точек пересечения параболы у = х ² + 4 и прямой х + у = 6.

4. Найдите нули функции у = х ³ + 2 х² - х - 2.

5. Решите систему уравнений:

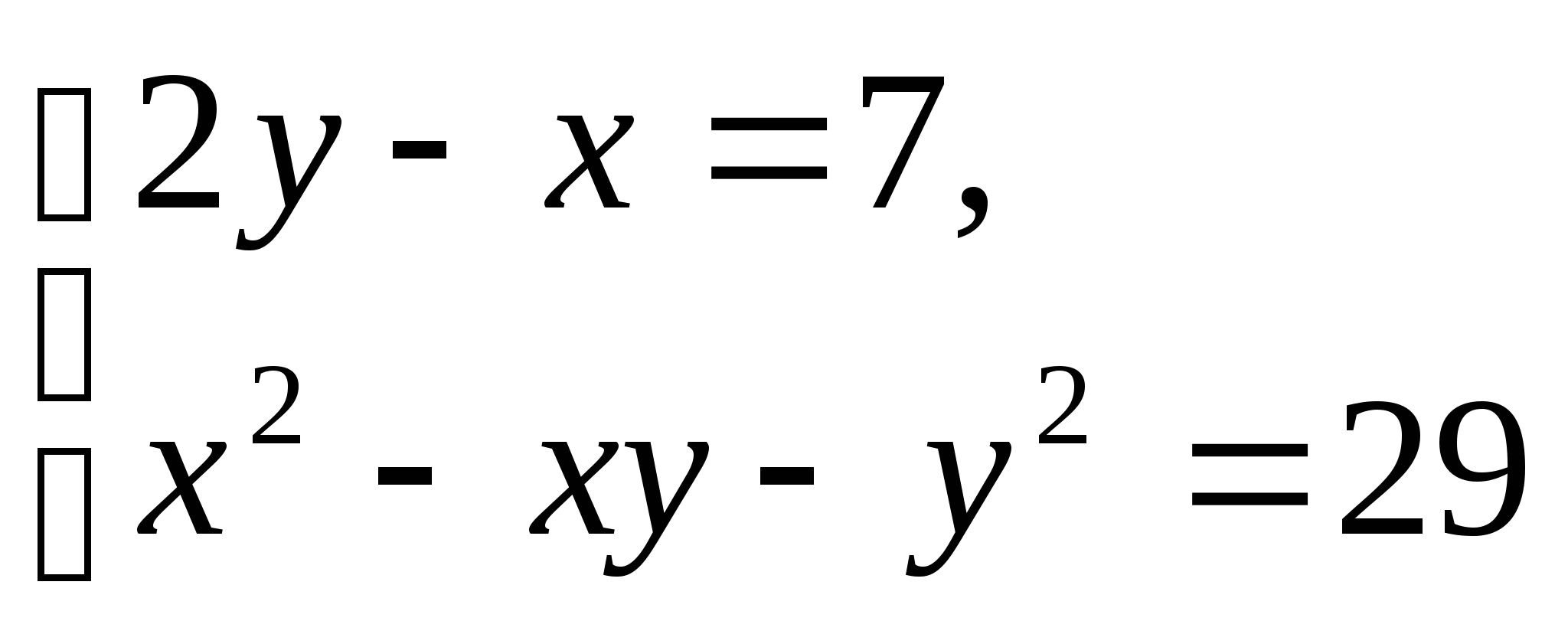
Вариант 2

1. Решите систему уравнений:

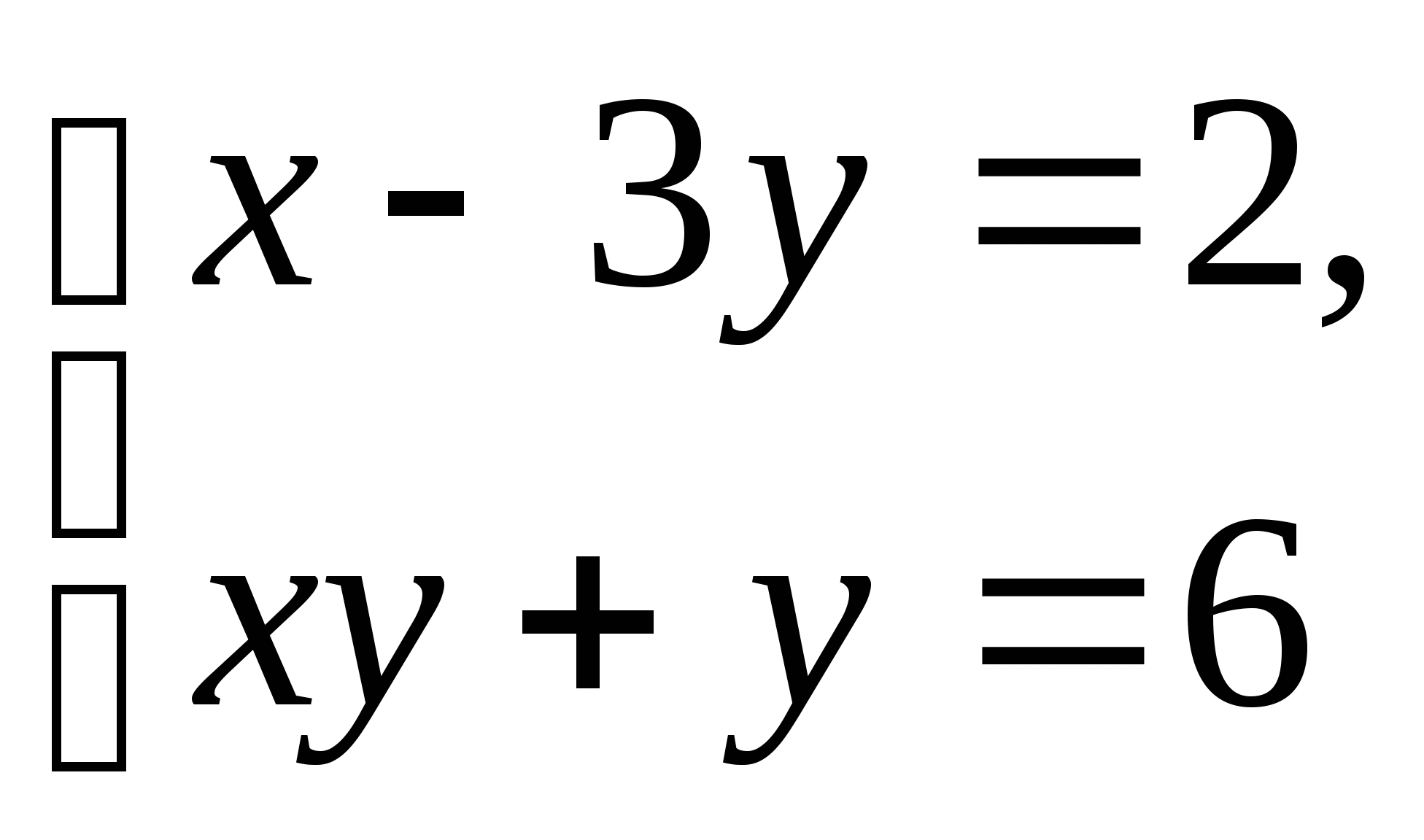
2. Одна из сторон прямоугольника на 2см больше другой стороны. Найдите стороны прямоугольника , если его площадь равна 120м ² .

3. Не выполняя построения, определите, найдите координаты точек пересечения окружности х ² + у ² = 10 и прямой х + 2у = 5.

4. Найдите нули функции у = х ³ - х² - 9х + 9.

5. Решите систему уравнений:

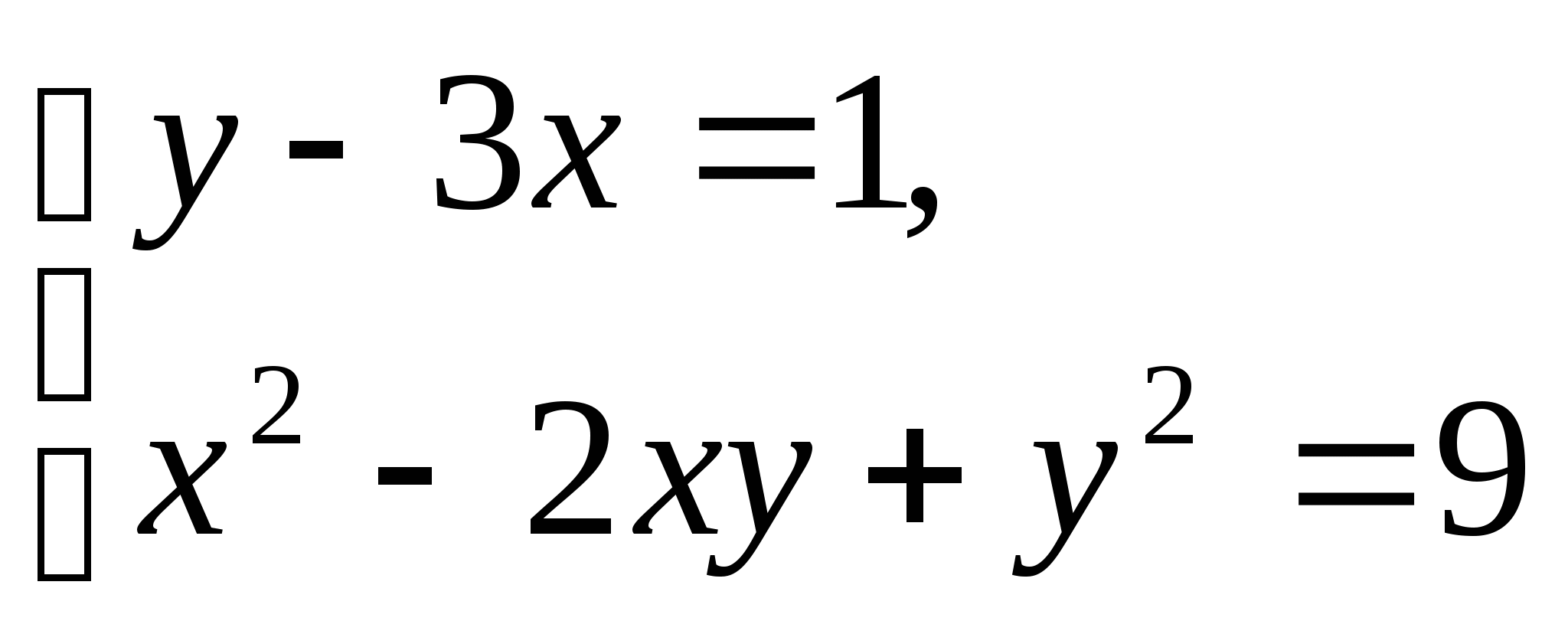
Контрольная работа №5 по теме

«Арифметическая прогрессия»

Вариант 1

1. Найдите двадцать третий член арифметической прогрессии, если , .

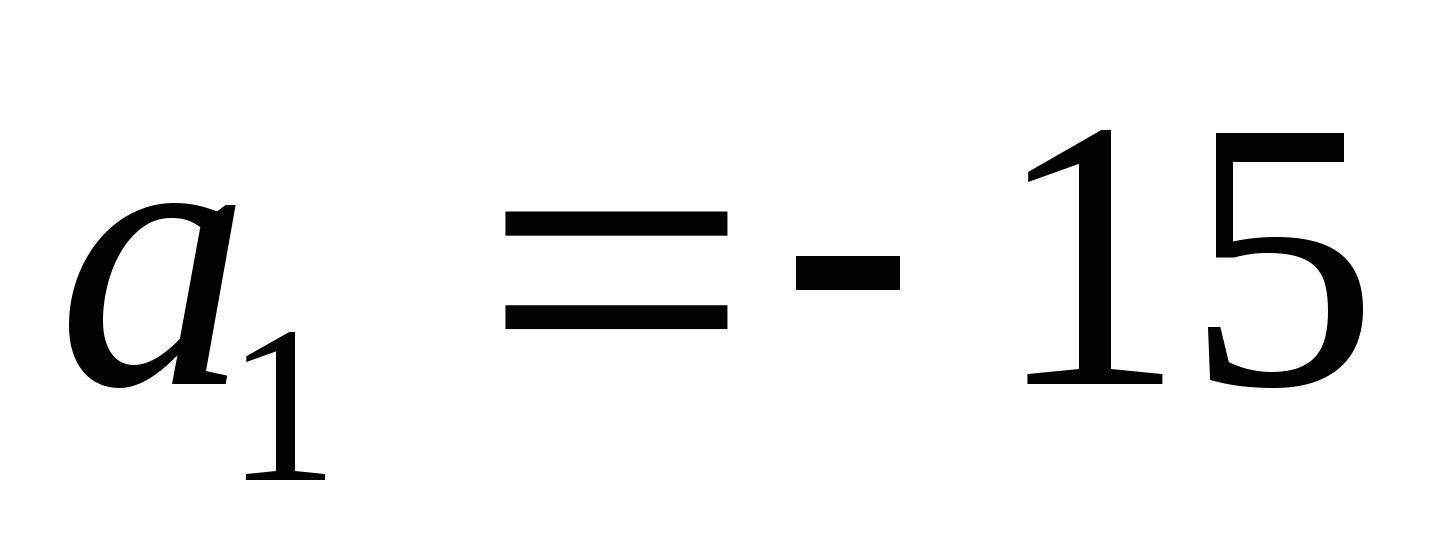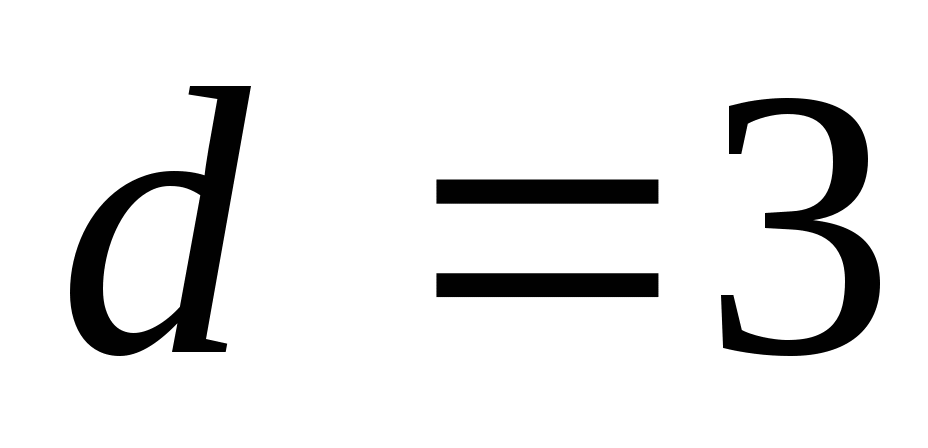2. Найдите сумму шестнадцати первых членов арифметической прогрессии: 8; 4; 0; …

3. Найдите сумму шестидесяти первых членов последовательности, заданной формулой .

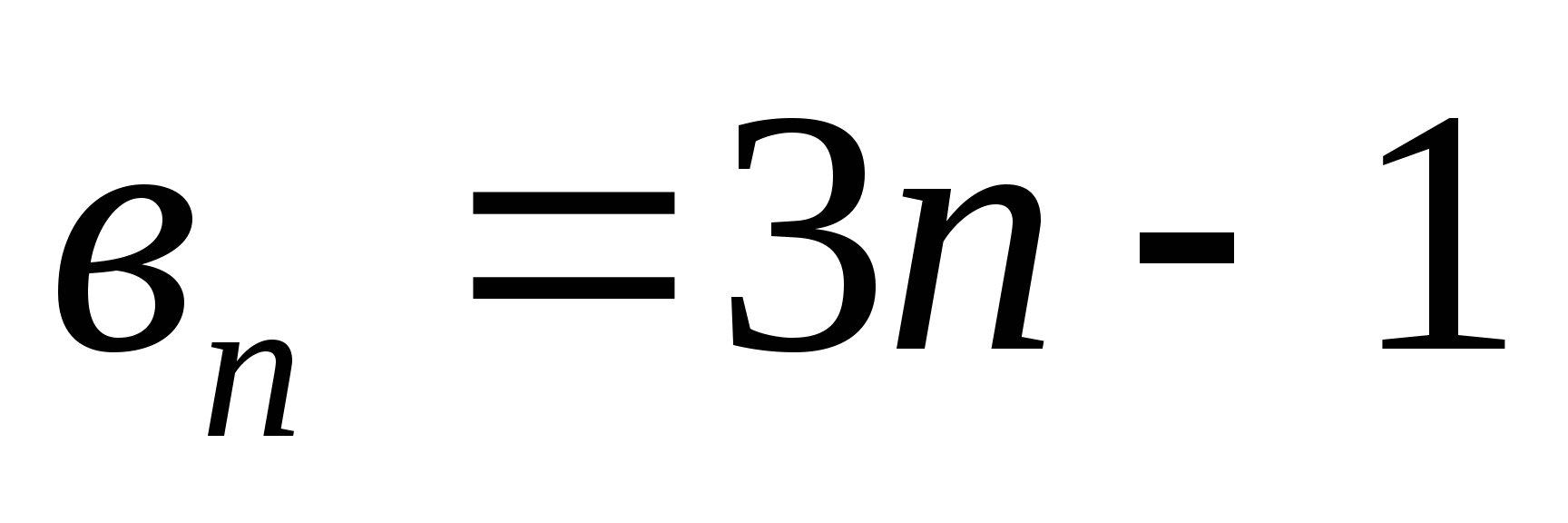4. Является ли число -54,5 членом арифметической прогрессии, в которой ; ?

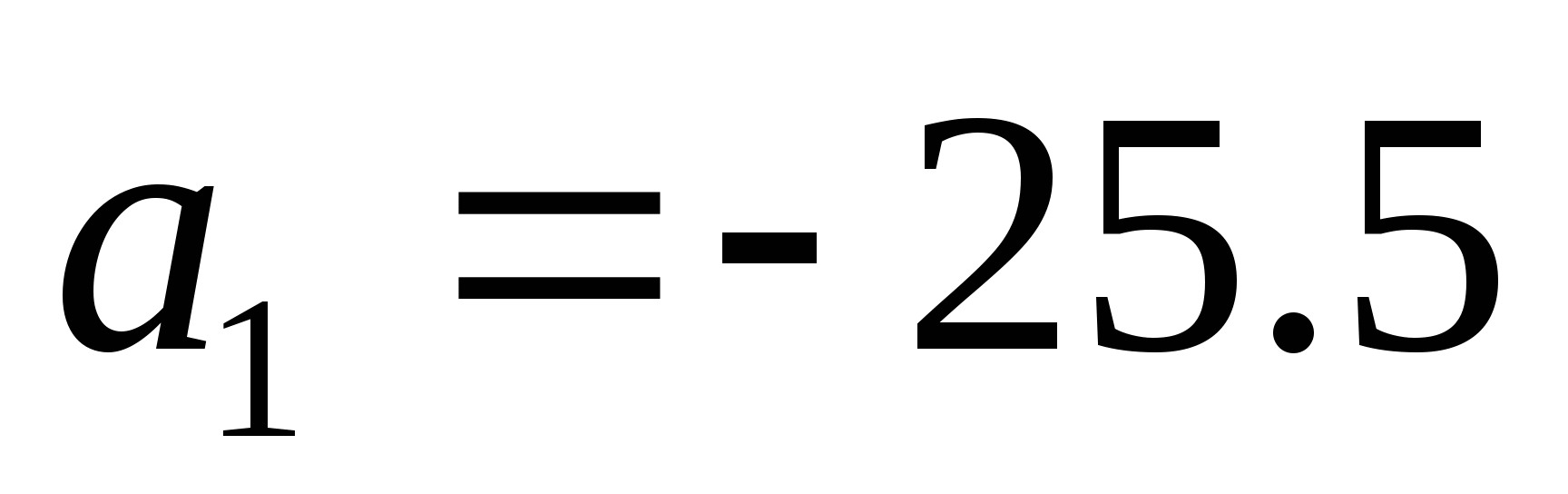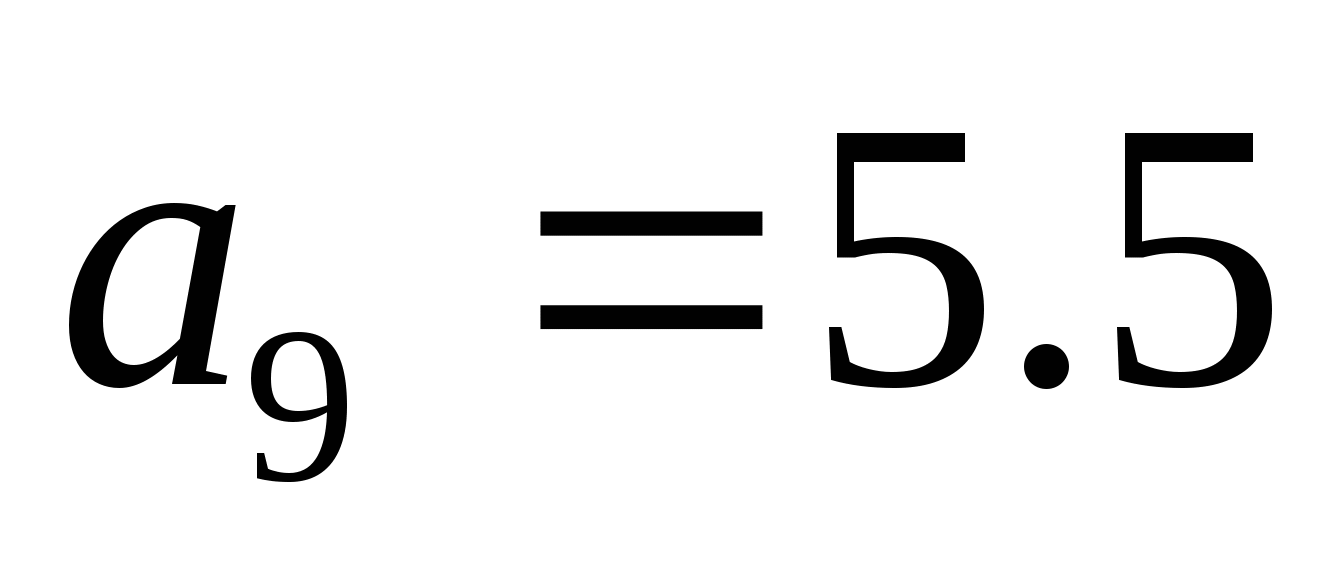5. Найдите сумму всех натуральных чисел, кратных 3 и не превосходящих 100.

Вариант 2

1. Найдите двадцать третий член арифметической прогрессии, если , .

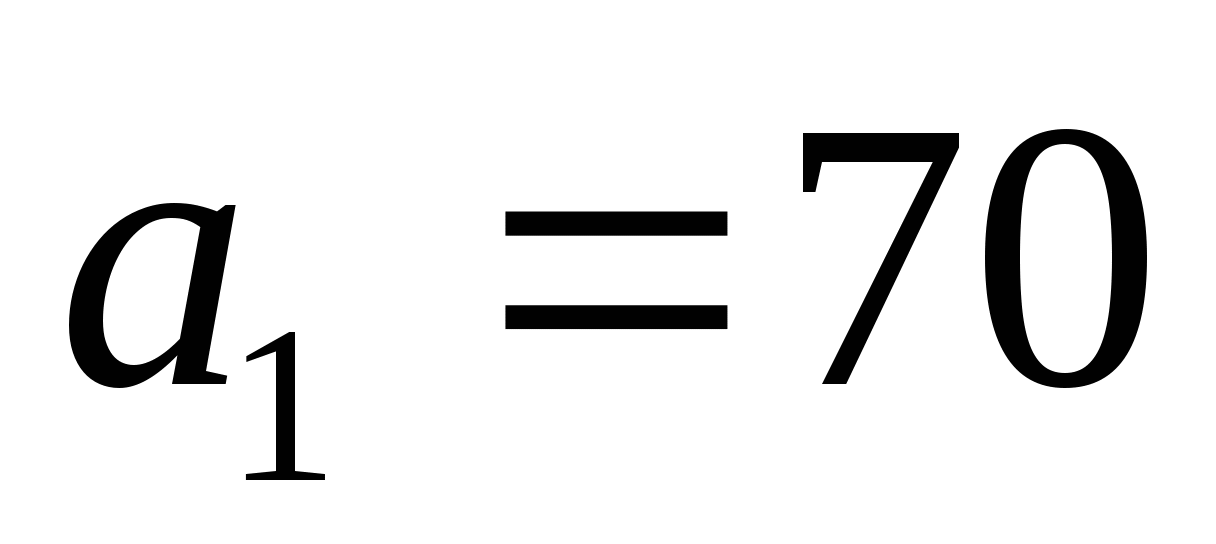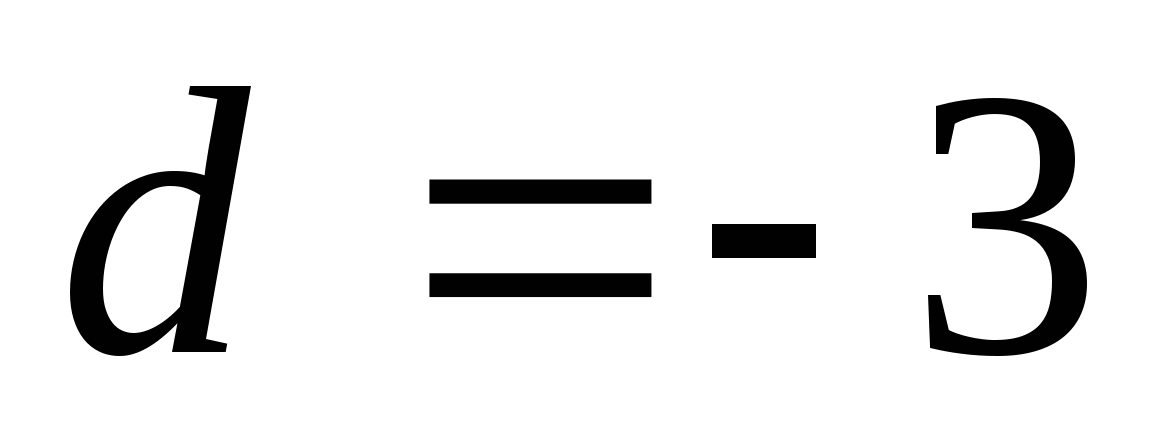2. Найдите сумму двадцати первых членов арифметической прогрессии: - 21; - 18; - 15; …

3. Найдите сумму шестидесяти первых членов последовательности, заданной формулой .

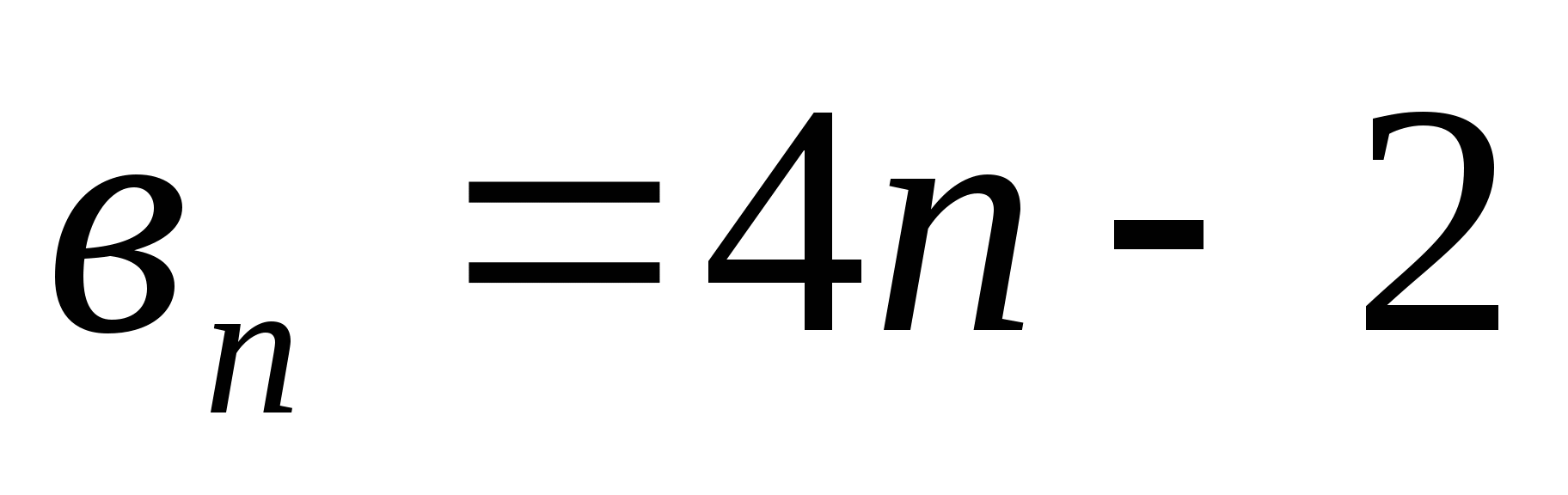4. Является ли число 30,4 членом арифметической прогрессии, в которой ; ?

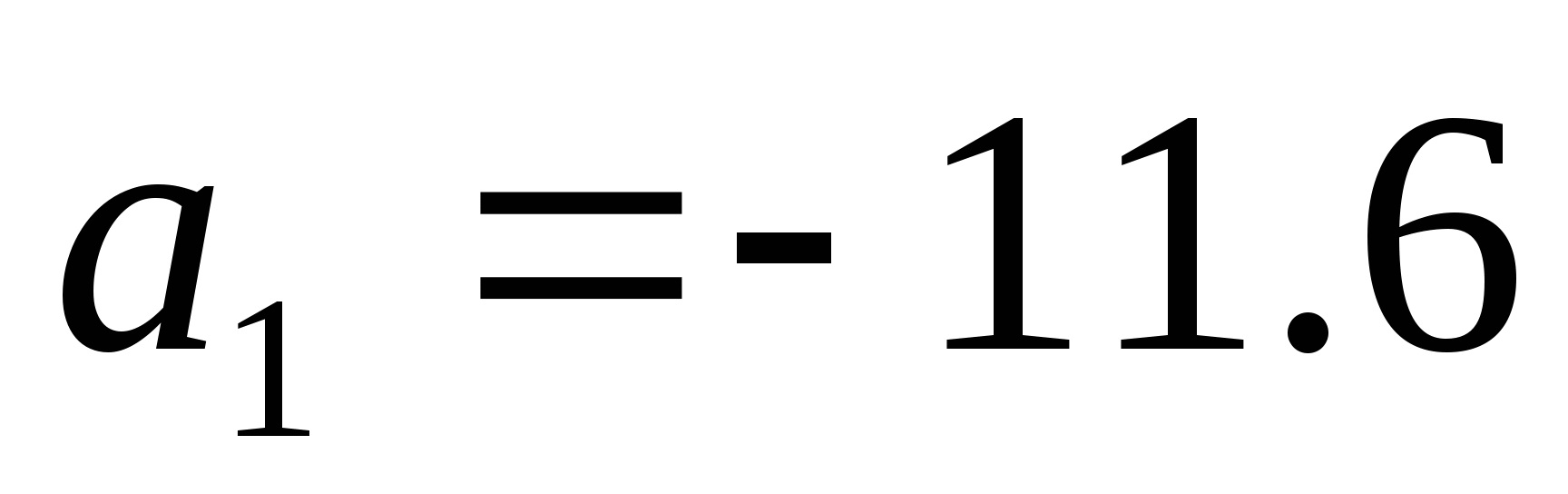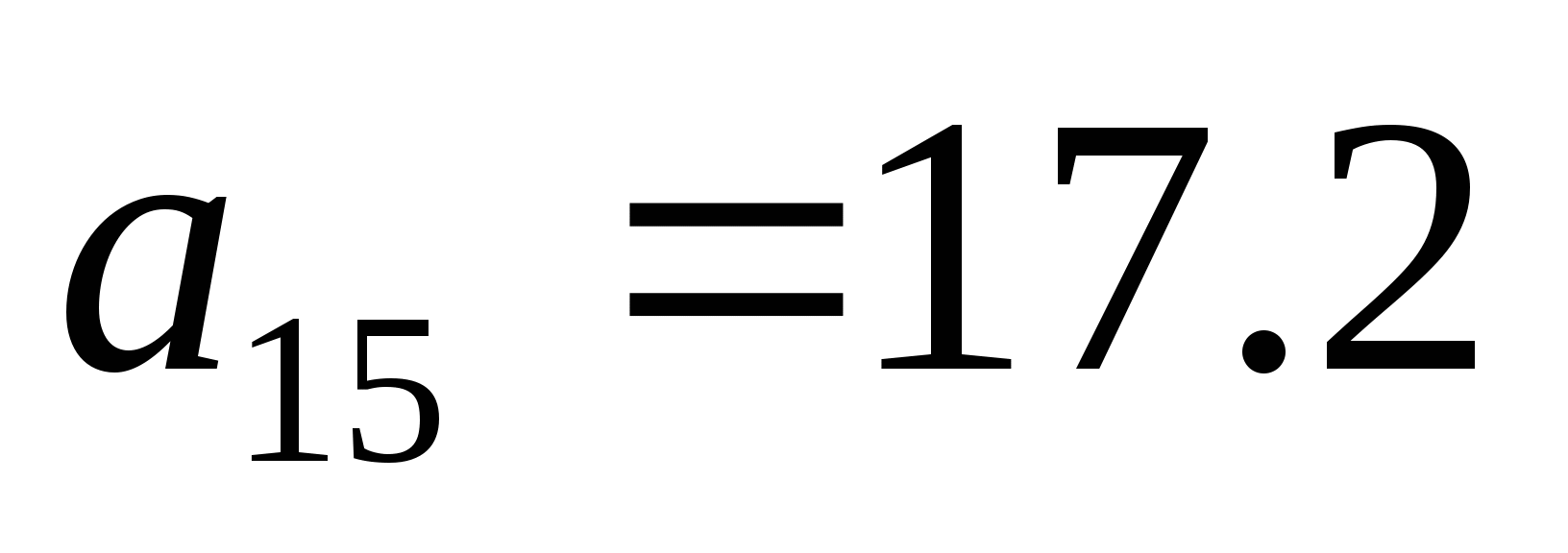5. Найдите сумму всех натуральных чисел, кратных 7 и не превосходящих 150.

Контрольная работа №6 по теме

«Геометрическая прогрессия»

Вариант 1

1. Найдите седьмой член геометрической прогрессии, если , .

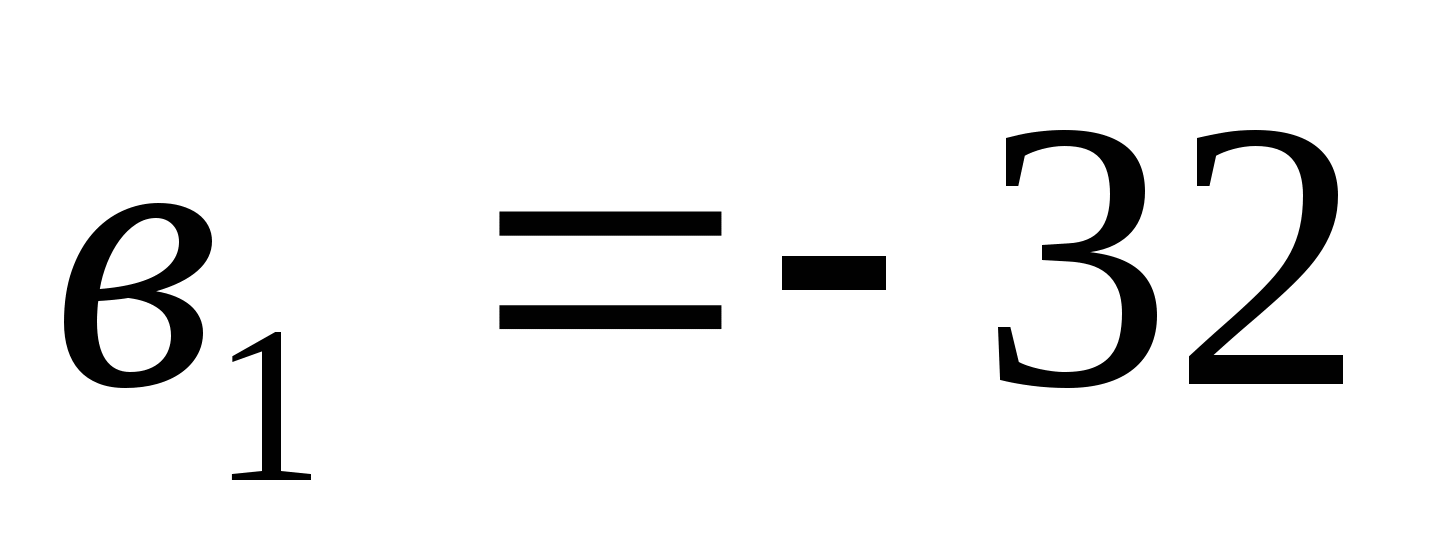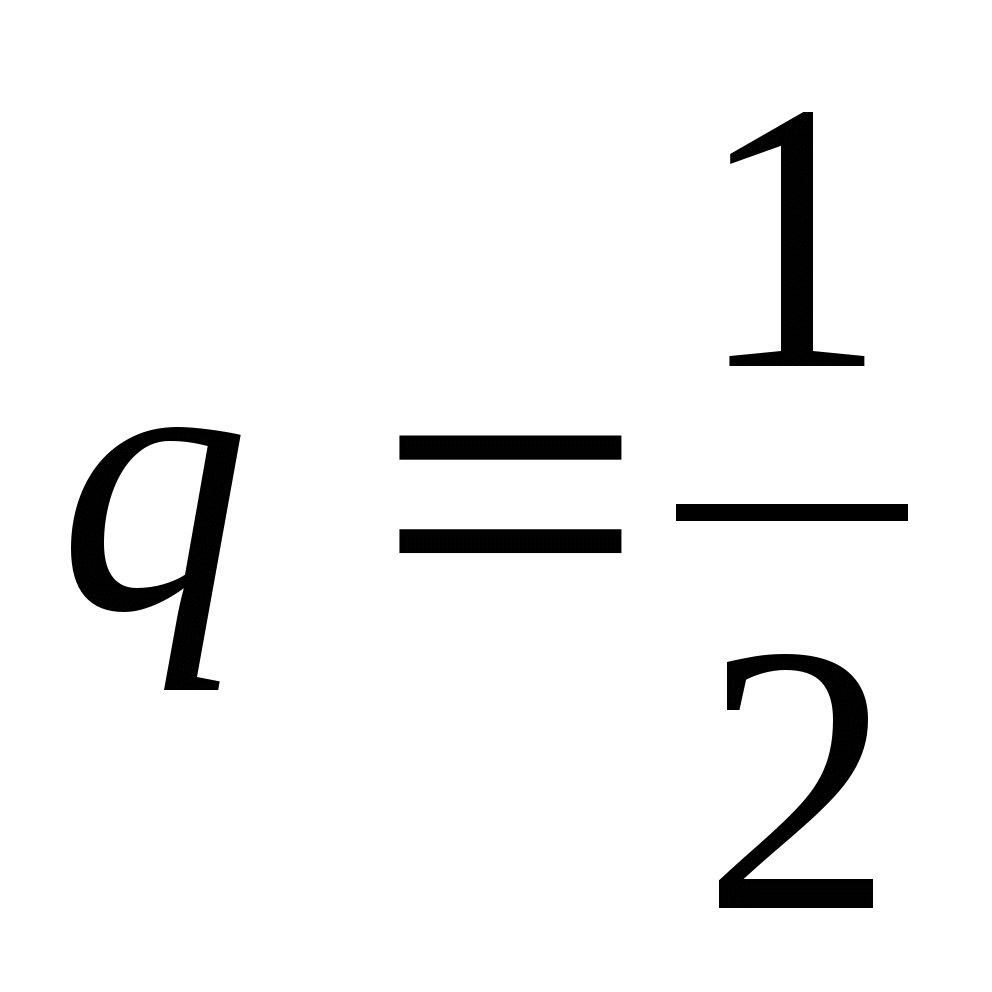2. Первый член геометрической прогрессии равен 2, а знаменатель 3. Найдите сумму шести первых членов этой прогрессии.

3. Найдите сумму бесконечной геометрической прогрессии : 24; -12; 6; ….

4. Найдите сумму девяти первых членов геометрической прогрессии с положительными членами, зная, что 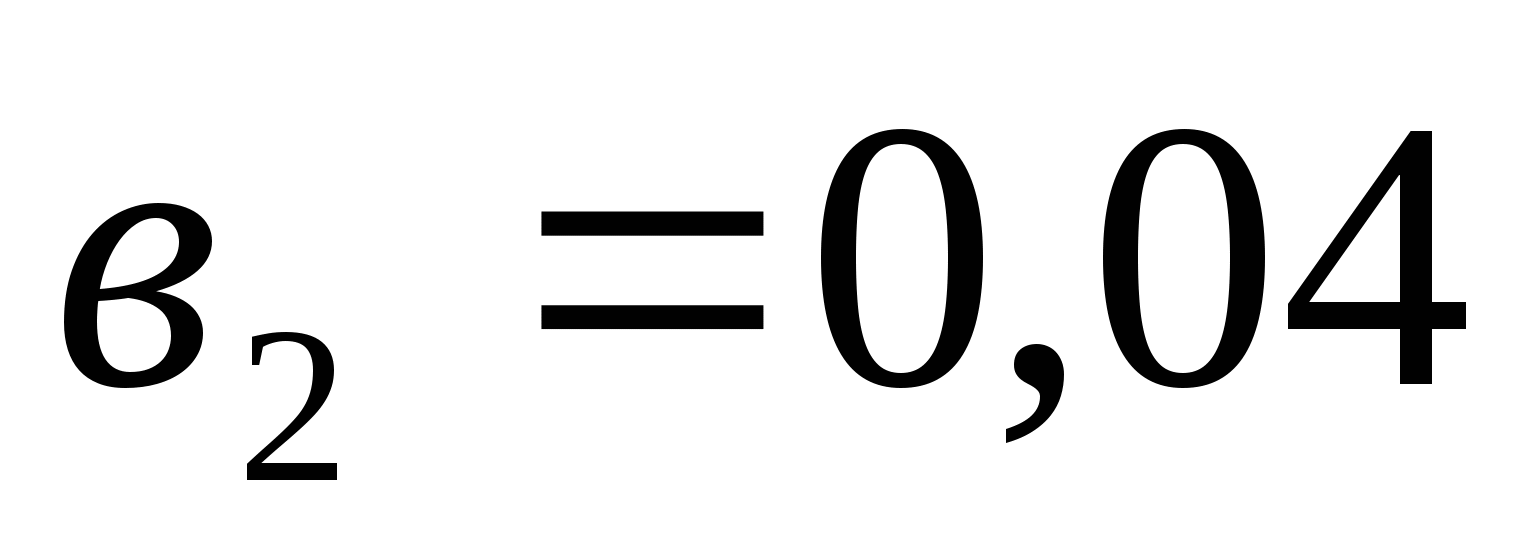и

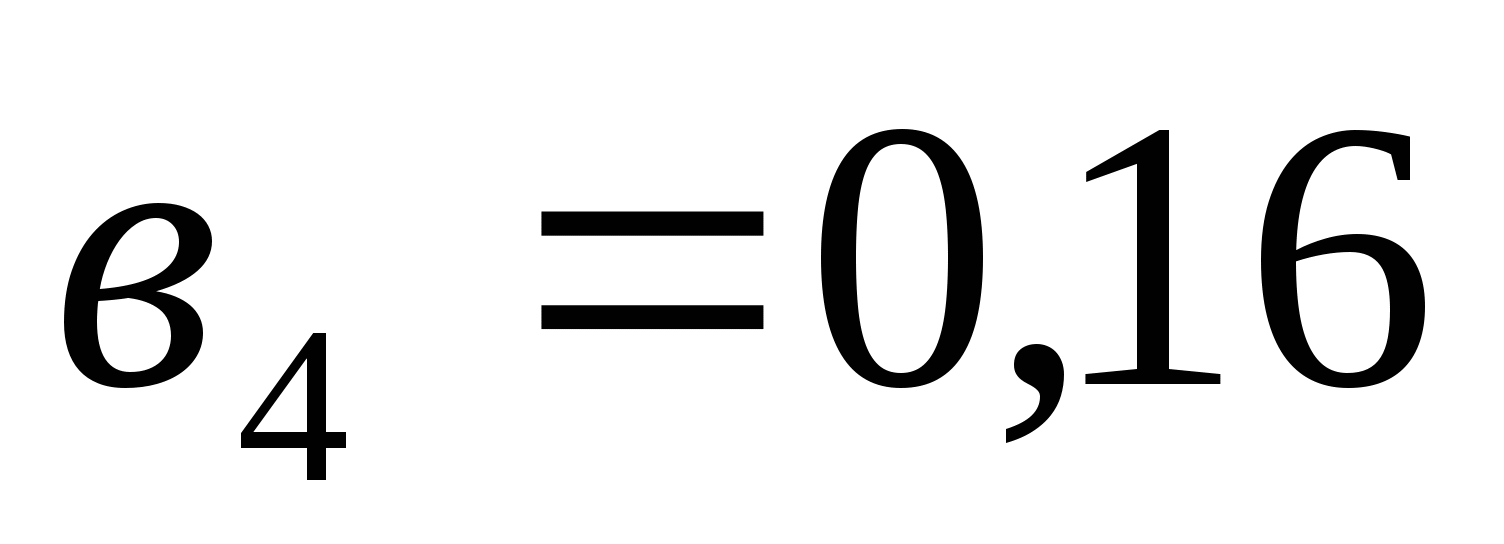
5. Представьте в виде обыкновенной дроби бесконечную дробь : а) 0,(27) ; б) 0,5(6).

Вариант 2

1. Найдите седьмой член геометрической прогрессии, если , .

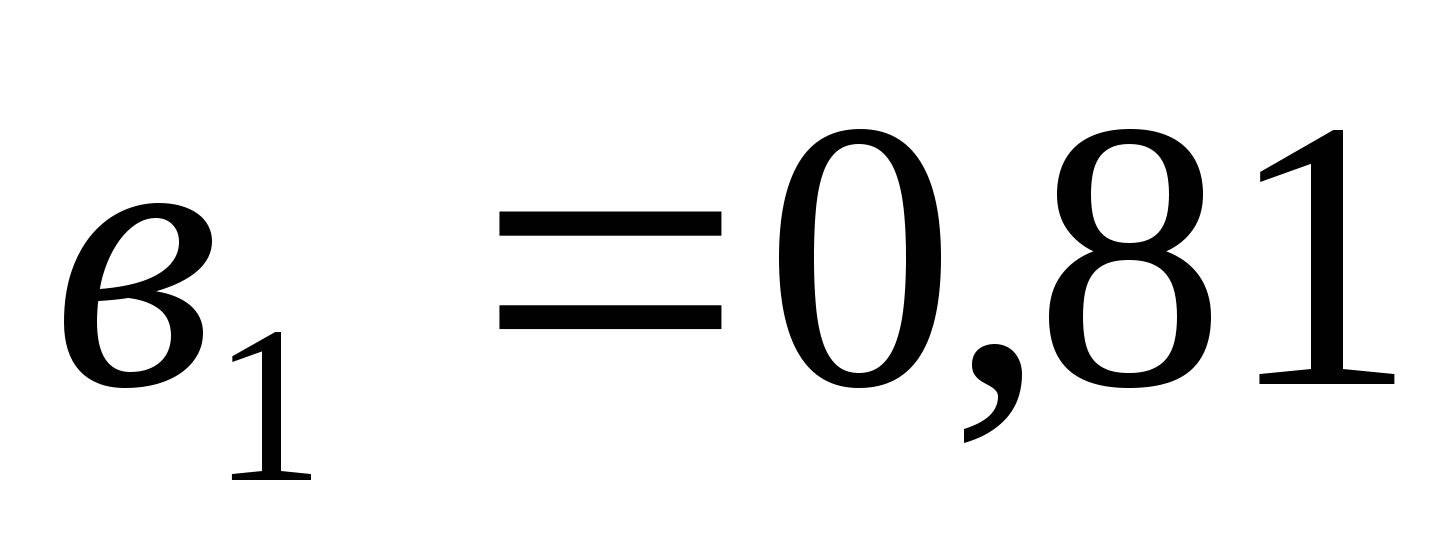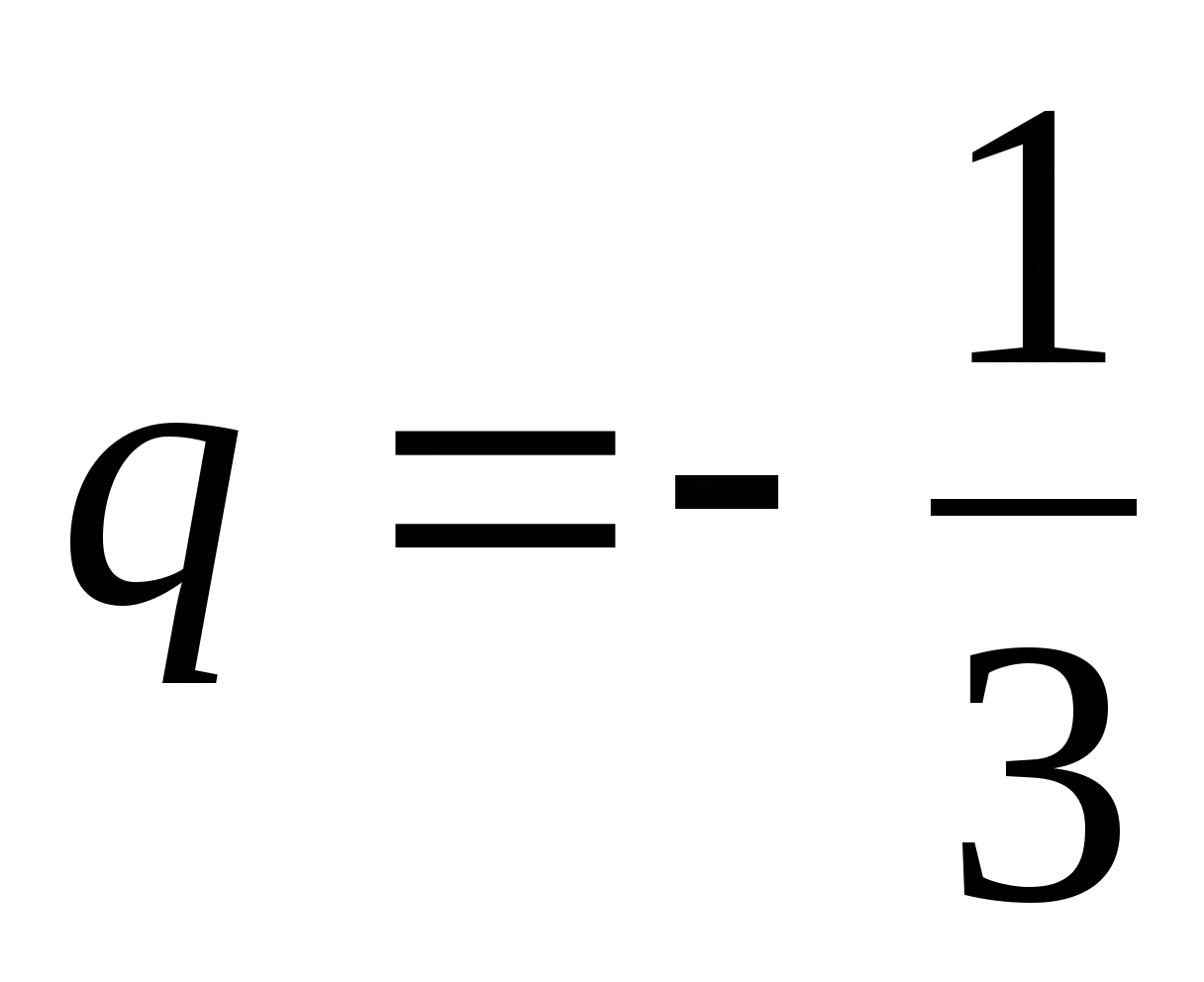2. Первый член геометрической прогрессии равен 6, а знаменатель 2. Найдите сумму семи первых членов этой прогрессии.

3. Найдите сумму бесконечной геометрической прогрессии : -40; 20; -10; ….

4. Найдите сумму восьми первых членов геометрической прогрессии с положительными членами, зная, что 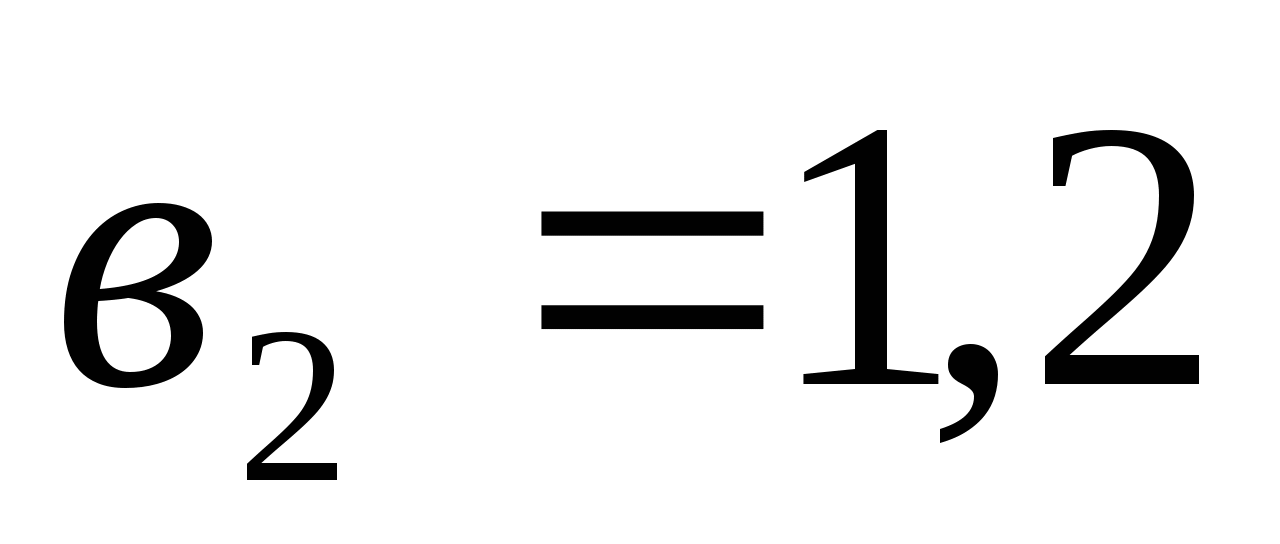и

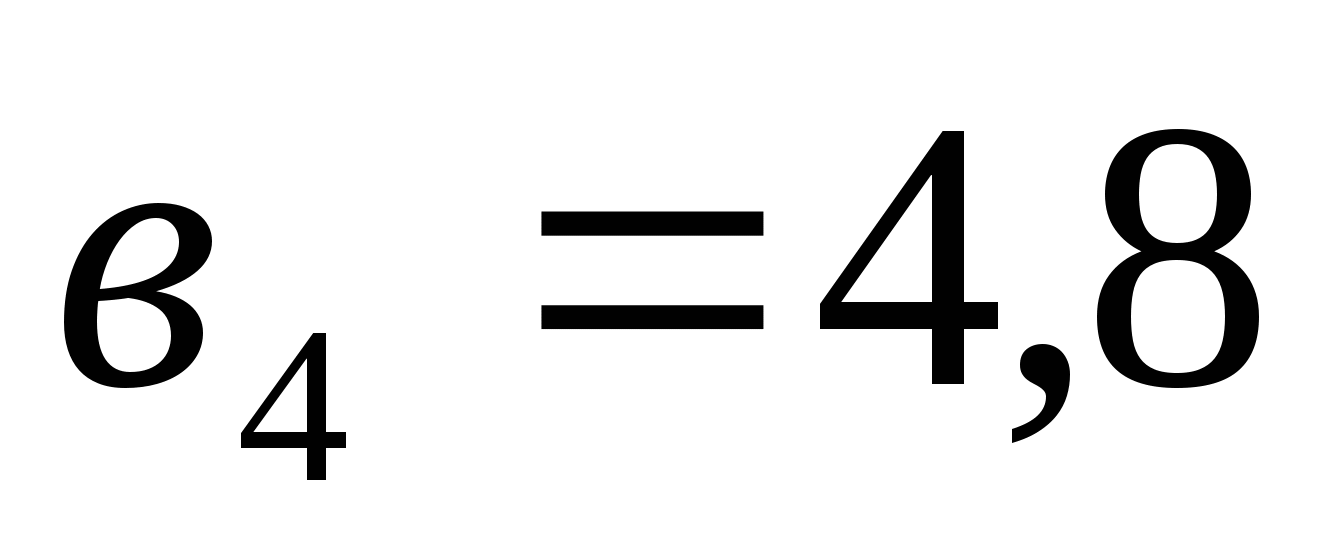
5. Представьте в виде обыкновенной дроби бесконечную дробь : а) 0,(153) ; б) 0,3(2).

Контрольная работа №7 по теме

«Элементы комбинаторики и теории вероятностей»

Вариант 1

1. Сколькими способами можно расставить 7 книг на полке?

2. Сколько различных шестизначных чисел можно записать с помощью цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 ( цифры в записи не повторяются)?

3. Сколькими способами можно выбрать трех дежурных в классе с 25 учениками?

4. Сколькими способами можно выбрать из четырех мальчиков и пяти девочек дежурных так, чтобы генеральную уборку делали три мальчика и две девочки?

5. В забеге участвуют 12 спортсменов. Сколько существует способов занять на финише 1-е, 2-е или 3-е место?

Вариант 2

1. Сколькими способами можно составить трехцветный полосатый флаг, если имеются ткани 6 цветов?

2. Сколько можно составить семизначных телефонных номеров из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 так, чтобы в каждом отдельно взятом номере все цифры были различны?

3. Сколькими способами можно заполнить карточку «Спортлото» ( зачеркнуть 6 номеров из 49)?

4. Сколькими способами можно выбрать из пяти мальчиков и шести девочек дежурных так, чтобы генеральную уборку делали два мальчика и три девочки?

5. В забеге участвуют 18 спортсменов. Сколько существует способов занять на финише 1-е, 2-е или 3-е место?

Итоговая контрольная работа №8

Вариант 1

1. Упростите выражение: .

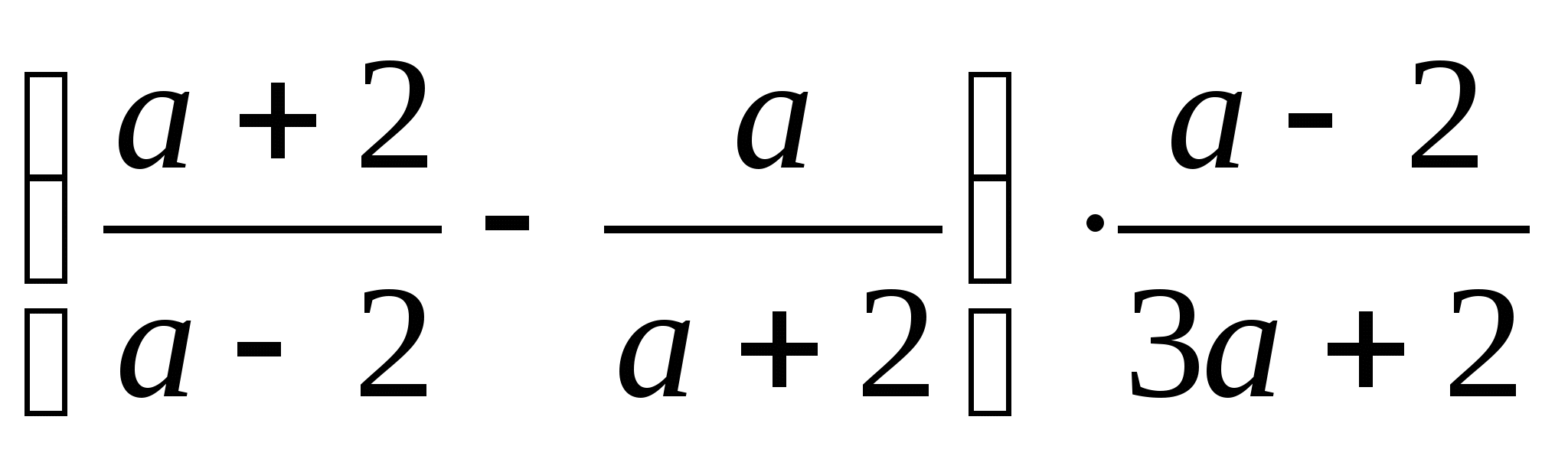2. Решите систему уравнений:

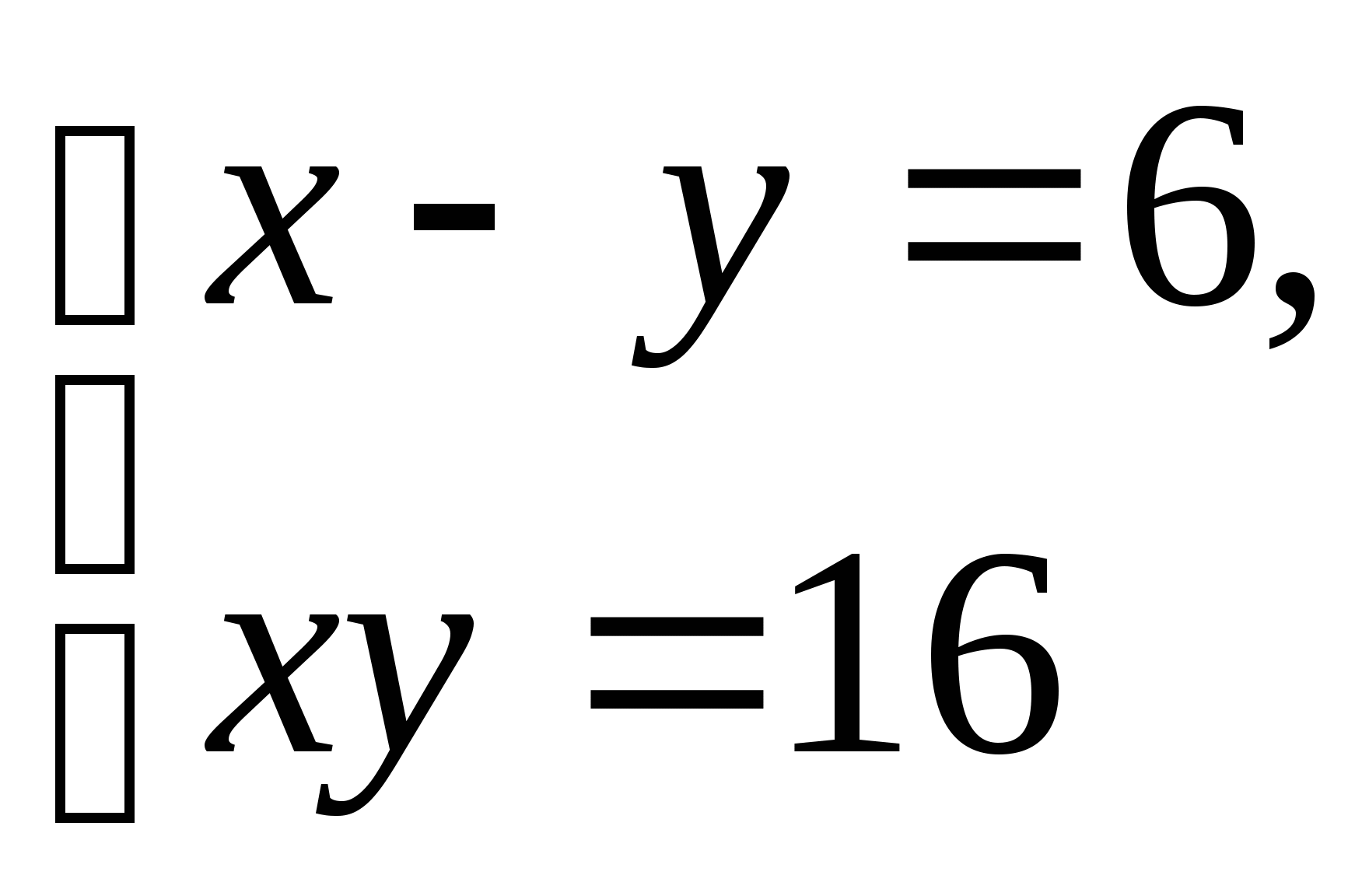
3. Решите неравенство 5х - 1,5 ( 2х + 3) < 4х + 1,5.

4. Постройте график функции у = х ² - 4. Укажите, при каких значениях х функция принимает положительные значения.

5. Бригада должна была изготовить 40 деталей к определенному сроку. Изготавливая в час на 8 деталей больше запланированного, бригада уже за 2ч до срока перевыполнила план на 8 деталей. Сколько деталей в час должна была изготовлять бригада по плану?

Вариант 2

1. Упростите выражение: .

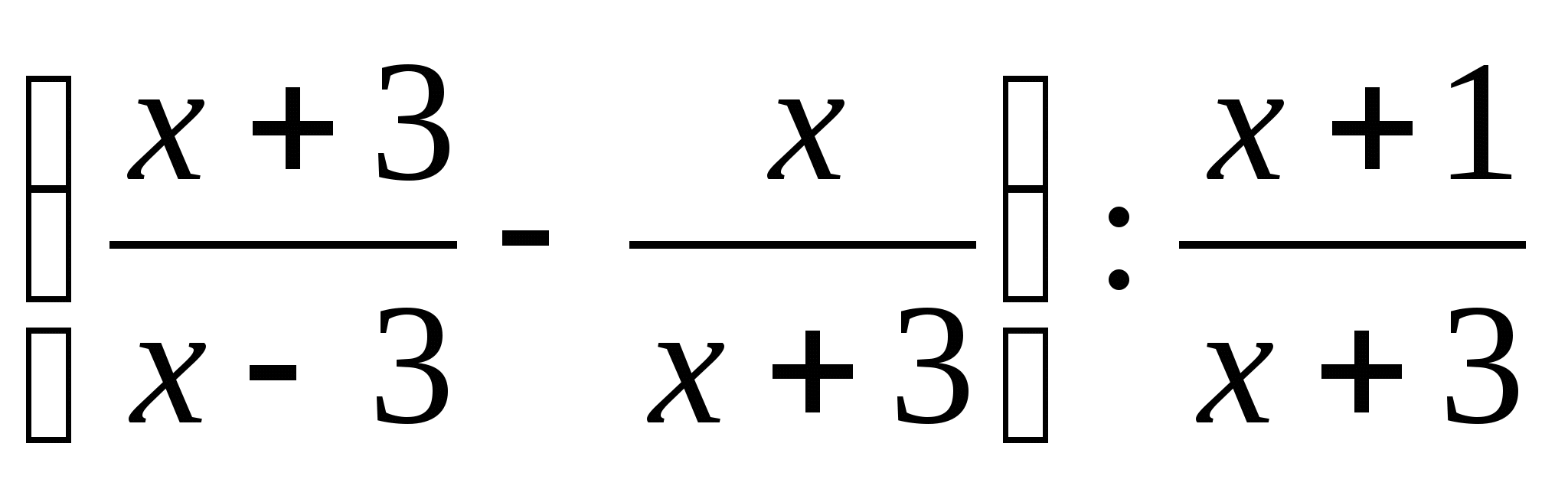2. Решите систему уравнений:

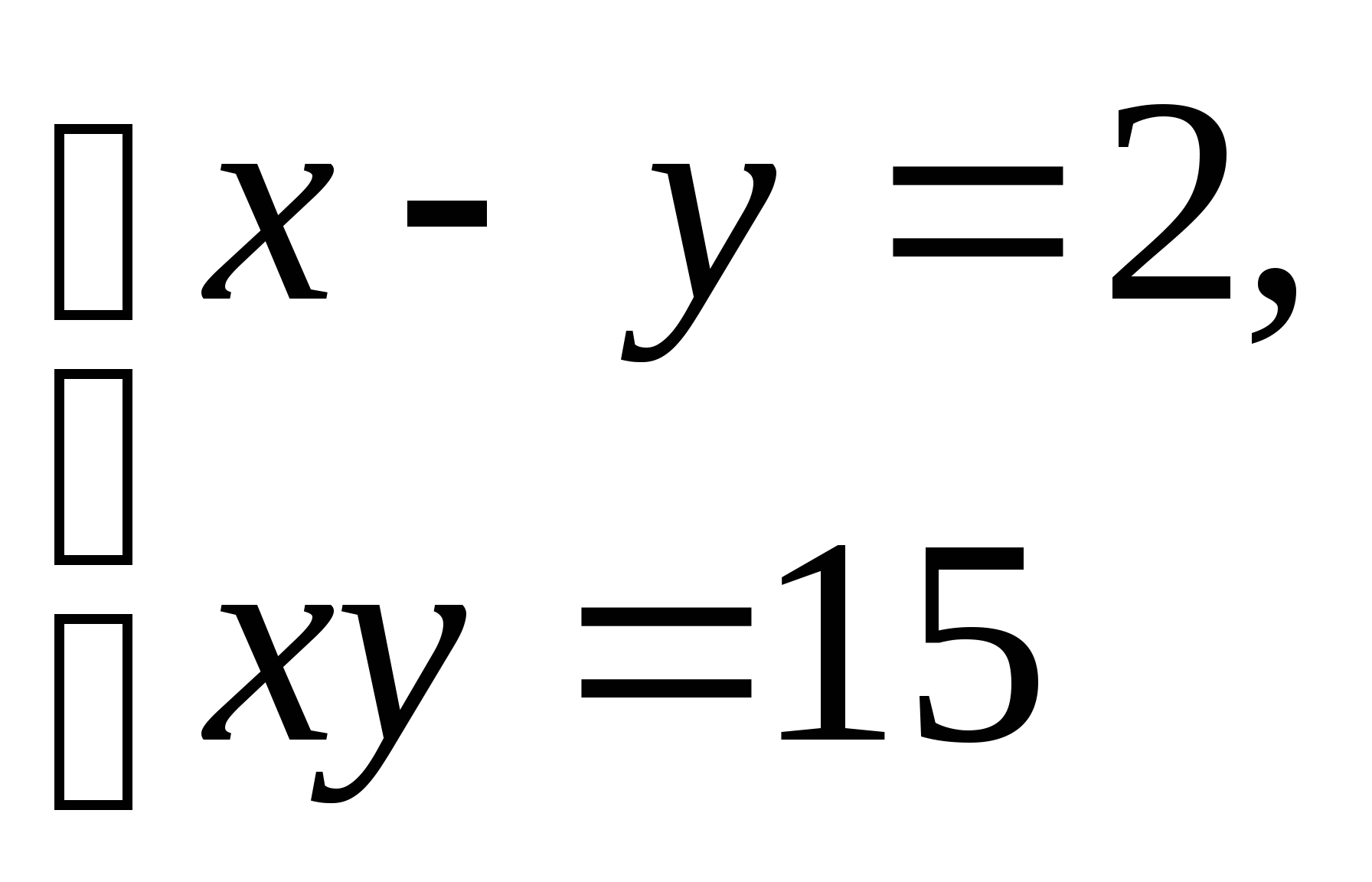
3. Решите неравенство 5х - 1,5 ( 2х + 3) < 4х + 1,5.

4. Постройте график функции у = - х ² -+ 1. Укажите, при каких значениях х функция принимает отрицательные значения.

5. Из пункта А в пункт В, расстояние между которыми 45км, выехал велосипедист. Через 30мин вслед за ним выехал второй велосипедист, который прибыл в пункт В на 15мин раньше первого. Какова скорость первого велосипедиста, если она на 3 км/ч больше скорости второго?