Разработка урока 7 класс 'Формулы сокращенного умножения'

Конспект урока.

Тема урока: «Формулы сокращенного умножения»

Предмет: математика.

Класс: 7.

Урок рассчитан на 45 минут.

Тип урока: формирование новых знаний.

Цель урока:

Вывести формулы квадрата разности, квадрата суммы; сформировать умение применять эти формулы для упрощения выражений.

Задачи урока:

• Обучающая: подвести обучающихся к выводу формул квадрата разности и квадрата суммы

• Развивающая: развивать коммуникативные способности обучающихся, навыки сотрудничества работы в группе; навыки самоконтроля

• Воспитательная: воспитывать интерес к предмету и к процессу обучения в целом

Оборудование: компьютер, мультимедийный проектор, интерактивная доска, презентация «Формулы сокращенного умножения»

Конспект урока

Этапы урока и их содержание

Деятельность

Время

учителя

обучающихся

1. Самоопределение к учебной деятельности (организационный момент)

Слайд 2:

ФЫРМОЛУ

- Добрый день, ребята!

- Попробуйте отгадать анаграмму. Какое слово зашифровано на доске?

- Формулы, верно!

- Формулы

1

мин

Слайд 3:

«У математиков существует свой язык - это формулы»

С.Ковалевская

- Начать сегодняшний урок мне хотелось бы со слов прекрасной женщины - великого математика Софьи Васильевны Ковалевской.

- Вы наверно, уже догадались, что речь сегодня на уроке пойдет о . . . формулах.

- Нам с вами предстоит познакомиться с новыми формулами

2. Актуализация знаний

Слайд 4:

№1. Устная работа.

m - n; xy; 2ab; d²; (a+b)²; x³ - y³; (c - d)³

-Прочитайте выражения, используя математические термины.

1) Разность чисел

m и n;

2) Произведение x и y;

3) Удвоенное произведение a и b;

4) Квадрат числа d;

5) Квадрат суммы чисел а и b;

6) Разность кубов чисел x и y;

7) Куб разности чисел

c и d.

9 мин

Слайд 5:

№2.Математический диктант

I.

1)Найдите квадраты выражений: 4х; 5у;

2) Найдите произведение: 4х и 5у;

3) Найдите удвоенное произведение: 4х и 5у;

4) Найти произведение многочленов

(4 - у) и (5 + х);

Слайд 6:

II. Запишите на математическом языке

5) Квадрат разности чисел m и 3;

6) Разность квадратов чисел y и 6;

7) Сумма кубов чисел b и 1.

Слайд 7:

- Запишите выражения в тетради

- Проверим ответы (анализ ошибок)

1 ученик выполняет задание на задней стороне доски, остальные - в тетрадях

1)16 х²; 25у²;

2) 20 ху;

3) 40ху;

4) 20+4х-5у-ху

5) (m - 3)²

6) y² - 36

7) b³ + 1.

Слайд 8:

№ 3. Возвести в квадрат устно, в тетрадь записать только ответ.

1. (- 7m⁶n³p)² =

2. (a + b)² =

3. (х - у)²=

1. Возвести одночлен - 7m⁶n³p

в квадрат.

2. Возвести сумму a и b в квадрат

3. Возвести разность х и у в квадрат

Возможные ответы детей:

1)49m¹²n⁶p²

2) a² + b²

3) х² - у²

3. Выявление причин затруднения и постановка цели деятельности

- Все справились с заданием?

-Чем задания 2) и 3) отличаются

от 1)?

- Кто выполнил 2) и 3), можете доказать свой ответ?

-Почему?

-Какая же цель нашего урока?

-Что для этого мы должны узнать?

1) - да,

2) и 3) - нет

- В 1 задании возводим в квадрат - одночлен, во 2 и 3 - многочлены.

-Нет

-Мы не умеем возводить в квадрат многочлены

Возможные ответы детей:

-Научиться возводить в квадрат многочлены;

-Научиться возводить в квадрат сумму и разность выражений ;

- Вывести новые формулы.

3 мин

Слайд 9:

Цель урока:

Вывести новые формулы

(a + b)²

(a - b)²

Квадрат суммы и квадрат разности.

Цель урока:

Вывести новые формулы, которые позволят быстро возводить в квадрат сумму и разность выражений.

-Какие названия можно дать данным формулам?

- Сформулируйте тему урока.

-Квадрат суммы и квадрат разности

- Формулы: квадрат суммы и квадрат разности.

4. «Открытие нового знания»)

Слайд 10:

Исследовательская работа (в группах).

-Задание группам (на карточках)

Выполнить умножение многочлена на многочлен, заметить закономерность, позволяющую вывести новую формулу для умножения многочленов.

1) (x + y)² =(x + y) (x + y)=

2) (c - d)² =(c - d) (. . .)=

3) (4 +a)² =(4 +a) (. . .)=

4) (m - 3)² =( . . . ) ( . . . )=

5) (4x + 5у)² =( . . . ) ( . . . )=

6) (2b - 1)² =( . . . ) ( . . . )=

ВЫВОД: Квадрат суммы двух выражений равен . . . . . . плюс их . . . произведение.

(a + b)² = … + … + …

Квадрат разности двух выражений равен . . . . . . минус их . . . произведение.

(a - b)² = … + … + …

- Сейчас вам предстоит сыграть роль исследователей и открыть новые формулы.

- Какие знания нам могут помочь в нашем открытии? Какую тему мы только что изучили?

- Можно ли квадрат разности и квадрат суммы представить в виде произведения многочленов? Каких многочленов?

- Ещё в глубокой древности было подмечено, что некоторые многочлены можно умножать короче, быстрее, чем остальные.

Так появились формулы сокращённого умножения. Их несколько. Сегодня вам предстоит открыть две из этих формул.

-Умножение многочлена на многочлен

- Да, в виде произведения одинаковых многочленов

Ученики самостоятельно работают в группах

12 мин

1) (x + y)² = . . .=

x² + 2хy+у²;

2) (c - d)² = . . . =с²-2сd+d²;

3) (4 +a)² = . . . =

16 +8а +а²;

4) (m - 3)² = . . . =

m²- 6m +9;

5) (4x + 5у)² = . . . =16х²+40ху+25у²;

6) (2b - 1)² = . . . =

4 b²- 4b+1

Слайд 11:

(a + b)² = а² + 2аb + b²

(a - b)² = а² - 2аb + b²

Слайд 12:

- Проверяем

(анализ результатов)

Ребята записывают свои ответы на доске.

- Какой вывод мы можем сделать?

-Что общего в ответах всех выражений?

- Удвоенное произведение с каким знаком?

- Как же записать формулы квадрата суммы и квадрата разности?

- Как прочитать эти формулы?

- Проверим свои ответы, открыв учебники на стр.113

- Запишем данные формулы в символической форме

Возможные ответы детей:

- Есть сумма квадратов и удвоенное произведение;

- 1 слагаемое - квадрат I выражения;

2 слагаемое - удвоенное произведение I и II;

3 слагаемое - квадрат II выражения;

- Если квадрат суммы, то с «+», квадрат разности с «- ».

- Ученики пишут на доске

Квадрат суммы двух выражений равен сумме их квадратов плюс их удвоенное произведение.

Квадрат разности двух выражений равен сумме их квадратов минус их удвоенное произведение.

Слайд 13:

Физминутка для глаз

Ребята выполняют физминутку

1 мин

Слайд 14, Слайд 15

Геометрическое истолкование формул

(a + b)² = а² + 2аb + b²

(a - b)² = а² - 2аb + b²

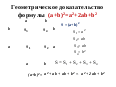
- Формулы квадрата суммы и разности двух выражений

знали еще в Древнем Вавилоне, а древнегреческие математики доказывали их средствами геометрии.

- Попробуем и мы с вами рассмотреть геометрическое доказательство формулы

(a + b)² = а² + 2аb + b²

-Построим квадрат со стороной a.

-Чему равна его площадь?

-Продолжим стороны квадрата на отрезок b, получим новый квадрат.

-Чему равна его площадь?

- Из каких фигур состоит большой квадрат со стороной a+b?

-Найдем их площадь

S₁ = a².

S =(a+b)²

-Квадрата со стороной a+b состоит

из квадрата со стороной a , квадрата со стороной b и двух прямоугольников со сторонами a и b

S₁ = a²

S₂= ab

S₃= ab

S₄= b²

Тогда ,

S = S₁ + S₂ + S₃ + S₄

или

(a+b)² = a² + ab + ab + b² = a² + 2ab + b².

3 мин

5. Первичное закрепление

Слайд 16

Учебник: № 28.6

а) (8х +3у)² =

б) (6m - 4n)²=

в) (9р - 2q)²=

г) (10z +3t)²=

Выполняют на доске с комментированием

а) 64х² +48ху+9у²;

б)36m² - 48mn+16n²

в) 81р² - 36pq+4q²;

г) 100z² +60z+9t².

5 мин

№ 28.2 (Устно)

а) (х +1)² =

б) (у - 2)²=

в) (а - 5)²=

г) (с +8)²=

Устно называют ответы

а) х² +2х+1;

б) у² - 4у +4;

в) а² - 10а+25;

г) с² +16с +64.

№ 28.4(Устно)

а) (-х +1)² =

б) (-z - 3)²=

в) (-n +8)²=

г) (-m -10)²=

Устно называют ответы

а) х² -2х+1;

б) z² + 6z +9;

в) n² - 16n+64;

г) m² +20m +100.

6.Самостоятельная работа (тест)

Слайд 17

№1.

задания

1

2

3

(t - m)²

t² -m²

t² +m²

t²-2tm+m²

(b +9)²

b²+9b+81

b²+18b+81

b²+81

(7a - 1)²

49a²-14a+2

49a²-14a-1

49a²-14a+1

(2x +3y)²

4x²+12xy+9y

4x²+6xy+9y²

4x²+12xy+9y²

Слайд 18

№ 2.

а) (* + *)² = 16p²+ * + 81n²;

б) (* - 2y)² = * - 28xy + *.

Слайд 19

Самопроверка.

№1 - 3233.

№2. а) (4p + 9n)² = 16p²+ 72pn + 81n²;

б) (7 - 2y)² = 49 - 28xy + 4y².

Ученики самостоятельно выполняют задания

Ученики проверяют себя, анализируют свои ошибки

4 мин

7. Включение в систему знаний и повторение

Слайд 20

- Для чего нужны нам формулы?

- А еще для чего? Посмотрите на картинку!

-Да, формулы квадрат суммы и квадрат разности используются иногда для быстрого счета.

- Давайте попробуем выполнить № 28.15 г, 28.16 г, 28.17 г.

- Для упрощения выражений

- Для быстрого счета

Ученики выполняют задания на доске

91²=(90+1) ² =

8100 + 180 + 1=82181

32²= (30+2) ² =

900 + 120 + 4=1024

58²= (60-2) ² =

3600 - 240 + 4=3364

3

мин

8. Итог урока. Рефлексия деятельности.

- Какие «открытия» мы совершили сегодня на уроке?

- Что использовали для «открытия» нового знания?

- Мы достигли поставленной цели?

- Проанализируйте свою работу на уроке.

Обучающиеся подводят итог урока, анализируют свою деятельность на уроке

3 мин

9.Домашнее задание

п.28, № 28.3, 28.5, 28.14(б, в),

28.16(б, в), 28.58^*;

*придумать примеры на применение формул квадрата суммы и квадрата разности.

Учитель комментирует домашнее задание

1 мин