- Учителю
- Конспект для 10 класса на тему Призма. Площадь поверхности призмы
Конспект для 10 класса на тему Призма. Площадь поверхности призмы
Призма. Площадь поверхности призмы
Класс: 10
Цель урока:
образовательная: познакомить учащихся с понятием призмы и видами призм, понятием площади полной и боковой поверхностей призмы, с доказательством теоремы о площади боковой поверхности прямой призмы, научить применять формулы для вычисления площадей при решении задач;
развивающая: развивать вычислительные навыки, логическое и пространственное мышление, речь учащихся;
воспитательная: воспитывать интерес к предмету, аккуратность при выполнении чертежей.
Форма урока: урок-лекция.
Тип урока: урок изучения нового материала.
Метод обучения: дедуктивно-репродуктивный метод.
Требования к ЗУН: учащиеся должны знать понятие призмы и виды призм, понятие площади полной и боковой поверхностей призмы, формулировку и доказательство теоремы о площади боковой поверхности прямой призмы, уметь применять формулы для вычисления площадей при решении задач по данной теме.
Оборудование: ПК, экран, проектор, мультимедиа презентация, бланки с лекциями.
Литература:
-
Геометрия, 10-11: Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. - 11-е изд. - М.: Просвещение, 2002 г.
-
Изучение геометрии в 10-11 классах: Метод. рекомендации к учеб.: Кн. для учителя /С. М. Саакян, В.Ф. Бутузов. - 2-е изд. - М. Просвещение, 2003. - 222 с.: ил. - ISBN 5-09-011836-1.
-
Методика и технология обучения математике. М.: Дрофа, 2005. - 416 с..
План урока:
I. Орг. момент (2 мин)
II. Актуализация знаний. (5 мин.)
III. Изучение нового материала (20 мин)
-
Формирование понятия призмы.
-
Виды призм: прямая, наклонная правильная.
-
Формирование понятия площадей полной и боковой поверхностей призмы.
-
Доказательство теоремы о площади боковой поверхности прямой призмы.
IV. Первичное закрепление материала. (13 мин)
V. Подведение итогов (5 мин)
VI. Домашнее задание. (1 мин)
Ход урока:
I. Орг. момент
Приветствие учеников, проверка готовности учащихся к уроку, проверка отсутствующих.
Учитель: (слайд 1) Мы с вами приступили к изучению новой большой главы: «Многогранники». Тема нашего сегодняшнего урока: «Призма». Мы поговорим о видах призм, познакомимся с понятием площади поверхности призмы, с теоремой о площади боковой поверхности прямой призмы и затем рассмотрим задачи.

II. Актуализация знаний.
Учитель: (слайд 2) Призма является многогранником. С какими многогранниками мы уже знакомы?
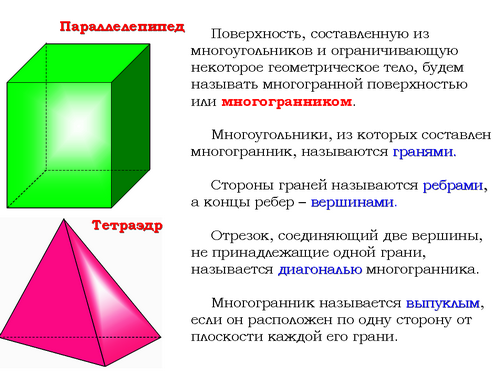
Ученик: Параллелепипед, тетраэдр.
Учитель:
- Что называется многогранником? Какая поверхность называется параллелепипедом? Тетраэдром?
- Что называют гранями многогранника? Вершинами? Ребрами? Диагональю?
- Какой многогранник называется выпуклым? (ответы детей, демонстрация слайда)
III. Изучение нового материала
Учитель раздает учащимся бланки с лекцией.
Учитель: Перейдем к изучению нового материала. Возьмите бланки с лекциями и запишите число и тему урока «Призма. Площадь поверхности призмы».
Запись на доске и в бланках.
Число
Классная работа
ТЕМА УРОКА: Призма. Площадь поверхности призмы
1. Формирование понятия призмы
Учитель: Призма тоже многогранник. Значит, в первую очередь, что мы будем понимать под призмой?
Ученик: Это поверхность, составленная из многоугольников.
Учитель: Какие элементы можно выделить у призмы?
Ученик: Основания, боковые грани, вершины, ребра.
Учитель: Теперь нам нужно разобраться, из каких именно многоугольников составлена поверхность и сколько их. У призмы 2 основания, основаниями являются два равных многоугольника, которые лежат в параллельных плоскостях, а остальные грани, боковые, - параллелограммы. Их столько, сколько и углов у многоугольника в основании.
Учитель: Итак, как мы можем сформулировать определение призмы?
Ученик: Призмой называется многогранник, составленный из двух равных многоугольников, лежащих в параллельных плоскостях, и параллелограммов
Учитель: Запишите в бланки это определение призмы.
Запись в бланках:
Призмой называется многогранник, составленный из двух равных многоугольников,
лежащих в параллельных плоскостях, и параллелограммов_
Учитель: (слайд 3) Рассмотрим два равных многоугольника А1А2…Аn и В1В2…Вn, расположенных в параллельных плоскостях α и β так, что отрезки А1В1, А2В2…АnBn, соединяющие соответственные вершины многоугольников, параллельны. Каждый из n четырехугольников А1А2В2В1, А1А2В2В1,…АnА1В1Вn является параллелограммом.
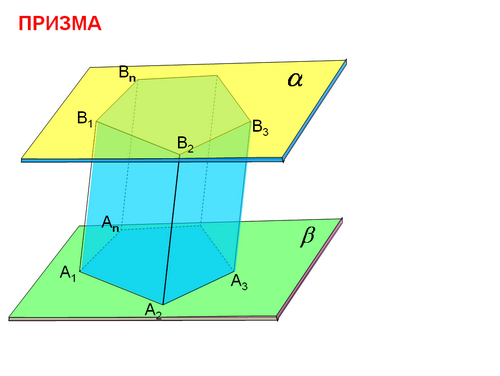
Учитель: Перед нами многогранник, составленный из двух равных многоугольников А1А2…Аn и B1B2…Bn, расположенных в параллельных плоскостях, и n параллелограммов A1A2B2B1, A2A3B3B2,…, AnA1B1Bn. Что мы получили?
Ученик: Призму.
Учитель: (слайд 3) Правильно. Многоугольники А1А2…Аn и В1В2…Вn называются основаниями, а А1А2В2В1, А1А2В2В1,…АnА1В1Вn - боковыми гранями призмы, а отрезки А1В1, А2В2…АnBn - ее боковыми ребрами.

Учитель: Подумайте и скажите, как можно обозначить пирамиду?
Ученик: А1А2…АnВ1В2Вn.
Учитель: Верно. Призму с основаниями А1А2…Аn и B1B2…Bn обозначают А1А2…АnВ1В2Вn и называют n-угольной призмой.
Учитель: Теперь сделайте соответствующие записи в ваших бланках.
Запись в бланках:
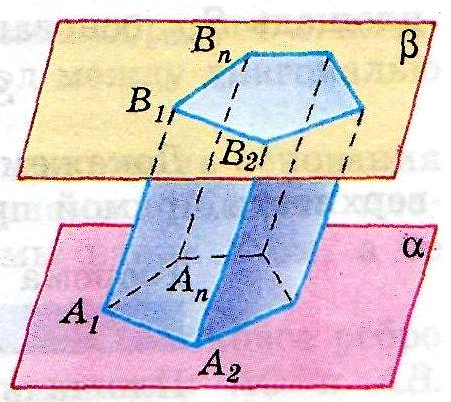
А1А2…АnВ1В2Вn - _призма_
Многоугольники А1А2…Аn и В1В2…Вn - _основания призмы_
Параллелограммы А1А2В2В1, А1А2В2В1,…АnА1В1Вn - _боковые грани
Отрезки А1В1, А2В2…АnBn - _боковые ребра призмы_
Учитель: (слайд 4) Запишем определение высоты призмы
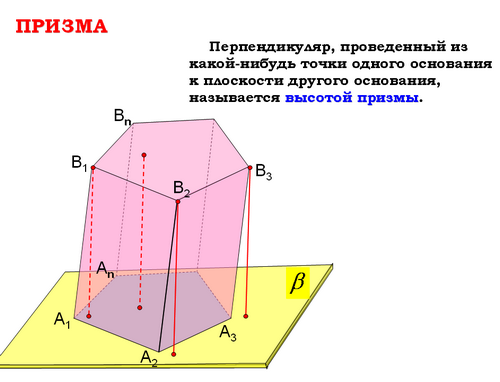
Запись в бланках:
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется _высотой_ призмы
2. Виды призм: прямая, наклонная правильная
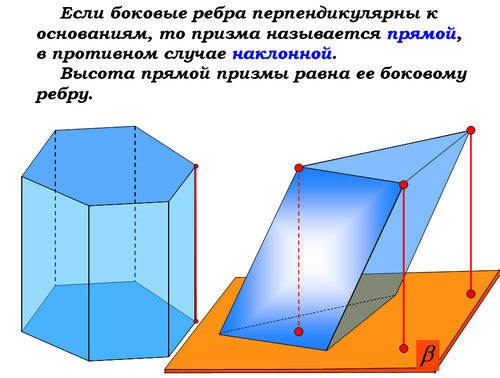
Учитель: (слайд 5) Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае - наклонной. Высота прямой призмы равна ее боковому ребру. Запишем это.
Запись в бланках:
Призма называется _прямой_, если боковые ребра призмы перпендикулярны к основаниям, в противном случае призма называется _наклонной_. Высота прямой призмы равна ее _боковому ребру .
Учитель: (слайд 6) Рассмотрим примеры призм.
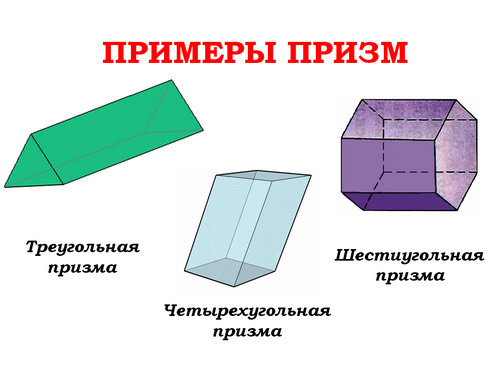
Учитель: Название призмы зависит от того, какие многоугольники лежат в её основаниях: треугольники - треугольная призма, пятиугольники - пятиугольная и т.д. Четырёхугольная призма является параллелепипедом.
Учитель: (слайд 7) А какая призма будет называться правильной?
Ученик: Если ее основания - правильные многоугольники.

Учитель: Правильно. Но изначально эта призма ещё должна быть прямой. У такой призмы все боковые грани являются равными прямоугольниками. Запишите это в свои бланки.
Запись в бланках:
Прямая призма называется _правильной_, если ее основания - правильные многоугольники. У такой призмы все боковые грани - _равные прямоугольники_.
3. Формирование понятия площадей полной и боковой поверхностей призмы.
Учитель: Подумайте и ответьте на вопрос: из чего состоит площадь полной поверхности призмы?
Ученик: Площадь полной поверхности призмы состоит из площадей оснований и площади боковой поверхности.
У
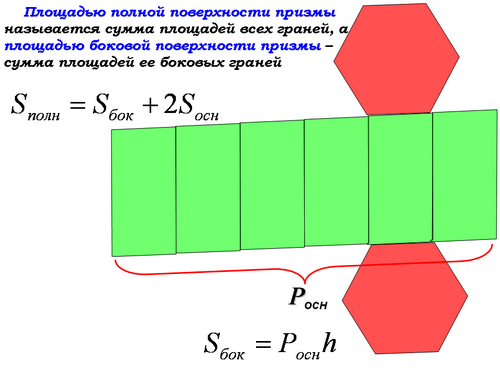
Sполн = Sбок + 2Sоснчитель: (слайд 8) Площадью полной поверхности призмы называется сумма площадей всех ее граней (т.е. основания и боковых граней), а площадью боковой поверхности призмы - сумма площадей ее боковых граней. Площадь полной поверхности выражается через площадь боковой поверхности и площадь основания призмы формулой: Запишем это.
Запись в бланках:
Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности призмы - сумма площадей ее боковых граней.
Sполн = Sбок + 2Sосн - площадь полной поверхности призмы
4. Доказательство теоремы о площади боковой поверхности прямой призмы.
Учитель: (слайд 9) Докажем теорему о площади боковой поверхности прямой призмы.

Учитель: Формулировка теоремы звучит так: «Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы». Это выражается формулой: Sбок = Ph. Сделайте записи в бланках.
Запись в бланках:
ТЕОРЕМА: _Площадь боковой поверхности прямой призмы равна произведению периметра
основания на высоту призмы.____________________________________________
Sбок = Ph - площадь боковой поверхности прямой призмы
Учитель: Боковые грани прямой призмы - прямоугольники, основания которых - стороны основания призмы, а высоты равны высоте h призмы. Площадь боковой поверхности призмы равна сумме площадей указанных прямоугольников. По-другому, чему равна?
Ученик: Равна сумме произведений сторон основания на высоту h. Вынося множитель h за скобки, получим в скобках сумму сторон основания призмы, то есть его периметр Р. Итак, Sбок=Ph.
-
Первичное закрепление материала.
Учитель: (Слайд 10) Среди изображенных тел выберите те, которые являются призмами, ответ обоснуйте.
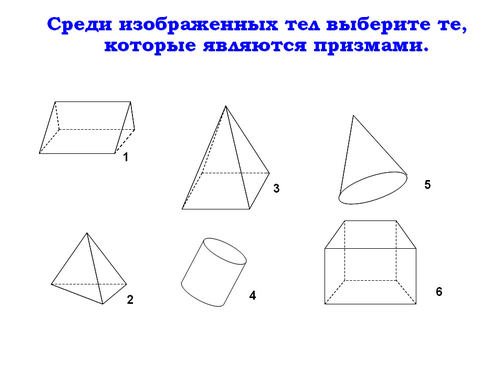
Учитель: (Слайд 11) Перейдем к решению задач.
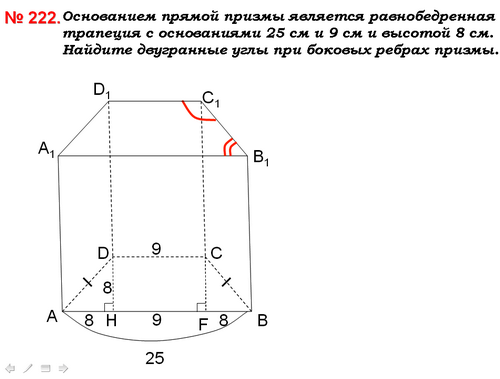
№ 222. Основанием прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 см и высотой 8 см. Найдите двугранные углы при боковых ребрах призмы.
Учитель: Сделаем рисунок и запишем, что нам дано и, что нужно найти.
Ученик: Нам дано: АВСDA1В1C1D1 - прямая призма, ABCD - равнобедренная трапеция, АВ = 25, СD = 9, DH = 8. Нужно найти А1В1C1 и В1C1В1 (АВC и ВCD).
Запись на доске (учителем) и в бланках (учениками):
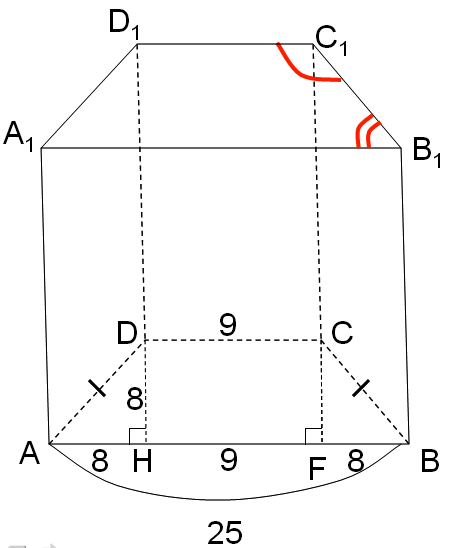
Дано: АВСDA1В1C1D1 - прямая призма, ABCD -трапеция, AD = BC, АВ = 25, СD = 9, DH = 8.
Найти: А1В1C1 и В1C1D1 (АВC и ВCD).
Решение.
Учитель: Что мы можем найти из условия задачи?
Ученик: Так как трапеция правильная, то А = В и C = D (А1 = В1, C1 = D1).
Учитель: Как мы можем найти эти углы?
Ученик: Рассмотрим равнобедренную трапецию ABCD с высотами DH и CF.
Учитель: HF = 9см, AH = FB = (25 - 9) : 2 = 8.
Запись на доске (учителем) и в бланках (учениками).
Учитель: Можно заметить, что ∆ADH = ∆CBF - прямоугольные и равнобедренные, следовательно DAB = ABC = 45° и значит D = C = 45° + 90° = 135°.
Запись на доске (учителем) и в бланках (учениками)
Учитель: Таким образом, ABC и А1В1C1 - линейные углы двугранного угла передней и боковой граней, ABC = А1В1C1 = 45°. BCD и В1C1D1 - линейные углы двугранного угла задней и боковой граней, BCD = В1C1D1 = 135°.
Запись задачи в бланках:
1) Т.к трапеция правильная, то А = В и C = D (А1 = В1, C1 = D1).
2) Т.к ABCD - равноб., HF = 9см, DH = CF = 8см, = > AH = FB = (25 - 9) : 2 = 8 см.
3) ∆ADH = ∆CBF - прямоуг. и равноб. = > DAB = ABC = 45° и значит D = C = 45° + 90° = 135°.
4) Т.о, ABC и А1В1C1 - лин.углы, ABC = А1В1C1 = 45°. BCD и В1C1D1 - лин.углы, BCD = В1C1D1 = 135°.
Ответ: 45°, 135°.
(Слайд 12) Учитель: Следующий № 221
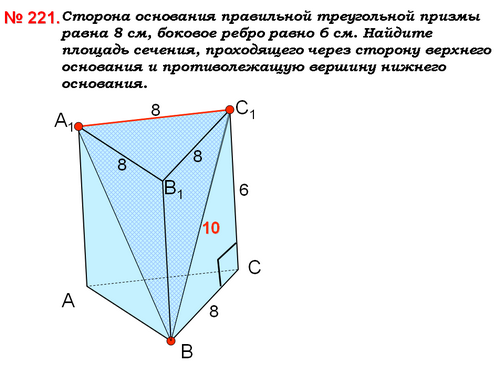
№ 221. Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
Учитель: Сделаем рисунок и запишем, что нам дано и, что нужно найти.
Ученик: Нам дана правильная треугольная призма АВСA1В1C1 со стороной основания равной 8см и боковым ребром равным 6см. Найти площадь сечения..
Запись на доске (учителем) и в бланках (учениками)
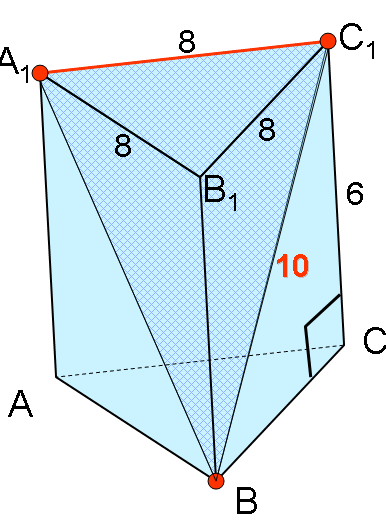
Дано: АВСA1В1C1 - правильная призма, AВ = BC = АС = 8см, СC1 = 6см.
Найти: S A1ВC1.
Решение.
Учитель: Так как АВСA1В1C1 - правильная призма, то боковые грани - равные прямоугольники, ∆A1ВC1 - равнобедренный. Что мы можем узнать, исходя из данных?
Ученик: Так как нам известна сторона основания и боковое ребро, то мы можем найти A1В = ВC1
Учитель: A1В = ВC1, ВC1 = √СВ2 + СС12, ВC1 = √82+62 = 10см
Запись на доске (учителем) и в бланках (учениками).
Учитель: Проведём высоту ВН, получим, что A1Н =НC1 = 4см. Как мы найдем ВН?
Ученик: По формуле Пифагора.
Учитель: ВН = √100 - 16 = 2√21см
Запись на доске (учителем) и в бланках (учениками):
Учитель: Итак, можем мы ответить на вопрос задачи?
Ученик: Можем, все данные для вычисления площади нам известны.
Учитель: S A1ВC1 = ½ * 8 * 2√21 = 8√21 (см2)
Запись на доске (учителем) и в бланках (учениками):
Запись задачи в бланках:
1) Т.к АВСA1В1C1 - правильная, то боковые грани - равн. прямоуг., ∆A1ВC1 - равноб. = > A1В = ВC1, ВC1 = √СВ2 + СС12, ВC1 = √82+62 = 10(см)
2) ВН┴ A1C1, A1Н =НC1 = 4см, значит ВН = √100 - 16 = 2√21(см) (По ф-ле Пифагора)
3) S A1ВC1 = ½ * 8 * 2√21 = 8√21 (см2)°.
Ответ: 8√21 (см2).
-
Подведение итогов
Вопросы учащимся:
- Что такое призма? Какие бывают призмы? На какие виды делятся?
- От чего зависит правильная призма или наклонная, прямая или нет?
- Сформулируйте теорему о площади боковой поверхности прямой призмы и назовите формулу, которой она выражается.
Оценка работы учащихся на уроке, выставление отметок.
-
Домашнее задание.
Учитель: запишите в дневники домашнее задание
§1, п.25, 27; №№ 223, 229.