Тема урока: Длина окружности. Число π. Длина дуги окружности

Тема урока: Длина окружности. Число π. Длина дуги окружности

Цель урока: вывести формулу, выражающую длину окружности через ее радиус; вывести формулу для вычисления длины дуги окружности с градусной мерой α

Задачи урока: решение задач по данной теме

Ход урока:

1 этап: Орг момент, приветствие, проверка домашнего задания

2 этап: Новая тема

Длина окружности

Рассмотрим правильный n - угольник B₁B₂…B_n , вписанный в окружность радиуса R, и опустим из центра O окружности перпендикуляры на все стороны многоугольника (рис. 2).

Поскольку площадь n - угольника B₁B₂…B_n равна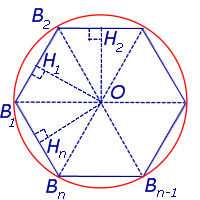

то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство: откуда вытекает формула для длины окружности радиуса R: C = 2πR.

Следствие. Длина окружности радиуса 1 равна 2π.

Длина дуги

Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Определение Числом π называют число, равное площади круга радиуса 1.

Замечание. Число π является иррациональным числом</, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

3 этап: решение задач

№ 312 стр 107 Если радиус окружности равен 5 см, то вычислите длину окружности

C=23,145=31,4 см

№ 313 стр 107 На сколько изменится длина окружности, если радиус увеличится на 1 см?

радиус увеличится на 2π, т. е. на 23,14=6.38

№ 314 стр 107 Вычислите длину окружности вписанной в квадрат

L=2πR R=a; (а -сторона квадрата) следовательно L= 2πa =πа

№ 315 стр 107 По радиусу окружности R=1 см вычислите длину дуги, соответствующей центральным углам: a)45° б)120°

1) = 2)=

L= = 0.125 см. L= = 0.(3)см Ответ: 1)1/8 см. 2)1/3 см.

№ 317 стр 107 Периметр правильного треугольника, вписанного в окружность, равен 18 см. найдите сторону квадрата, вписанного в эту окружность.

Тогда сторона правильного треугольника равна 18/3=6(см). Тогда запишем формулы для нахождения радиуса окружности, пусть сторона квадрата равна b:

4 этап: подведение итогов

5 этап: домашнее задание: № 316 № 318 стр 107