Муниципальное образование Крыловский района село Шевченковское

Муниципальное бюджетное образовательное учреждение

средняя общеобразовательная школа №4

имени Черкашина Евгения Валентиновича

села Шевченковского муниципального образования Крыловский район

ПЕДАГОГИЧЕСКИЙ ИЗМЕРИТЕЛЬНЫЙ МАТЕРИАЛ

по элективному курсу «Избранные вопросы математики»

Разработчик учитель математики

МБОУ СОШ №4 Лысенко В.И.

Вариант №1

1. Установите соответствие между функциями и их производными:f (х) = 6+cos x

f (х) = 6х+cos x

f (х) = 6 -cos x

а) f '(х) = - sin x

б) f '(х) = sin x

в) f '(х) = 6-sin x

2. Чему равна производная функции y = arcctg x+arcsin x в точке х₀ = 0?:

а) -2;

б) 0;

в) 2;

г) 1.

3. Установите соответствие между функциями и их производными:f (х) = (3х+1)³

f (х) = (3х+1)²

f (х) = (2х+1)³

а) f '(х) = 6 (3х+1)

б) f '(х) = 6 (2х+1)²

в) f '(х) = 9 (3х+1)²

4. Чему равна вторая производная функции f (х) = 5х+x²?

Ответ внесите в поле

5. На рисунке представлен график производной функции y = f '(х)

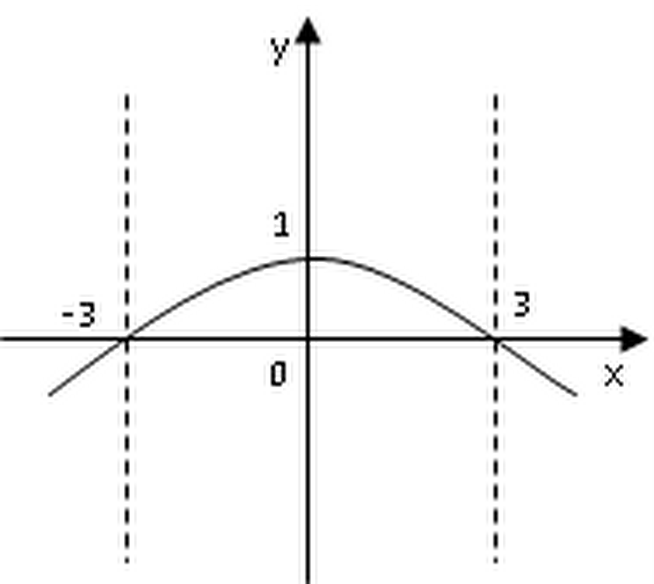
Выберете правильный вариант ответа:

а) х = 3 - точка минимума;

б) х = - 3 - точка максимума;

в) х = 0 - точка максимума;

г) х = - 3 - точка минимума.

6. Укажите две функции, определенные на всей числовой прямой и имеющие точку перегиба х_о = 1. Знаки производных второго порядка указаны на рисунках.а)

-

+

-

-

>

f ''(х)

-1

0

1

х

б)

-

-

-

+

>

f ''(х)

-1

0

1

х

в)

-

-

+

-

>

f ''(х)

-1

0

1

х

г)

-

-

+

+

>

f ''(х)

-1

0

1

х

7. Дана функция у = 2х⁴- 3х - 5. Установите соответствие между производными функции в соответствующих точках и их значениями.у' (-1)

у' (1)

у' (0)

а) - 3

б) 5

в) -11

8. Какой вид имеет множество всех первообразных функции у = ?

а) ;

б) 3 ln х⁷ + С;

в) ;

г) .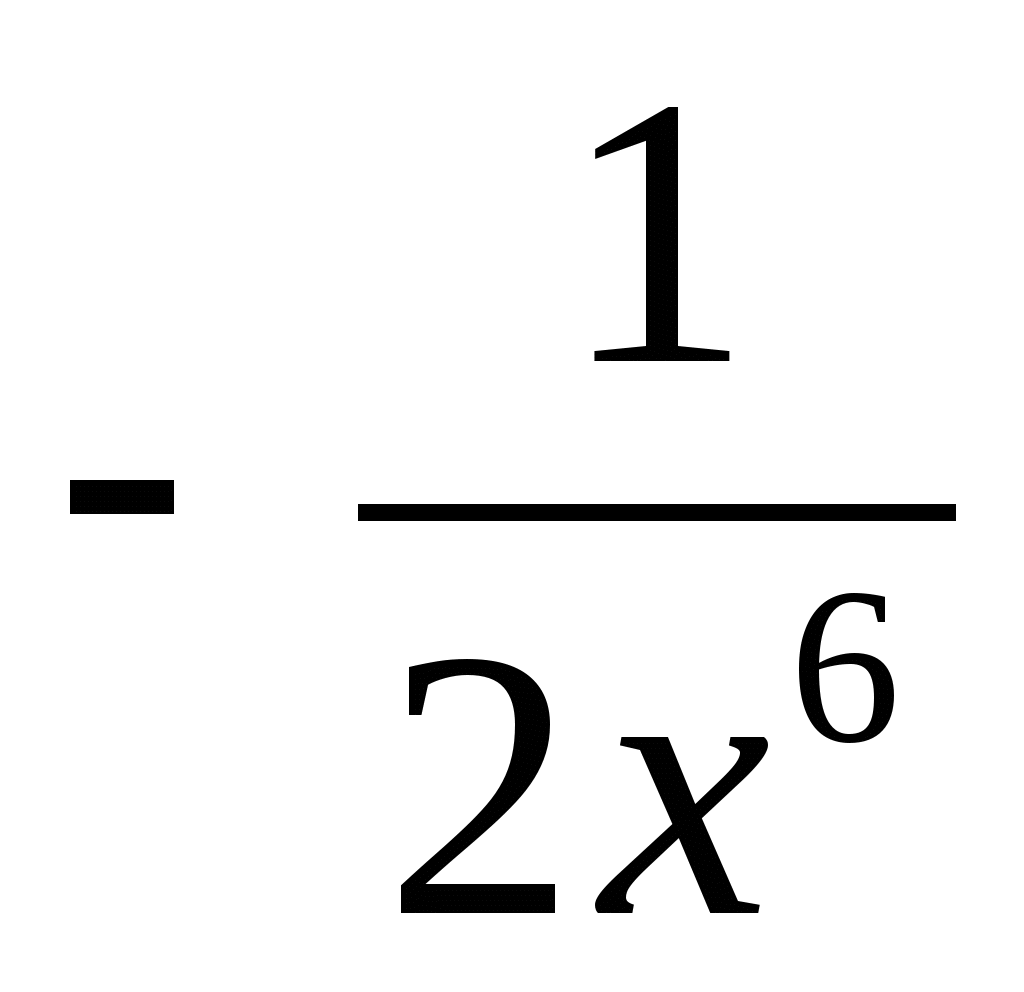

9. Чему равен интеграл ?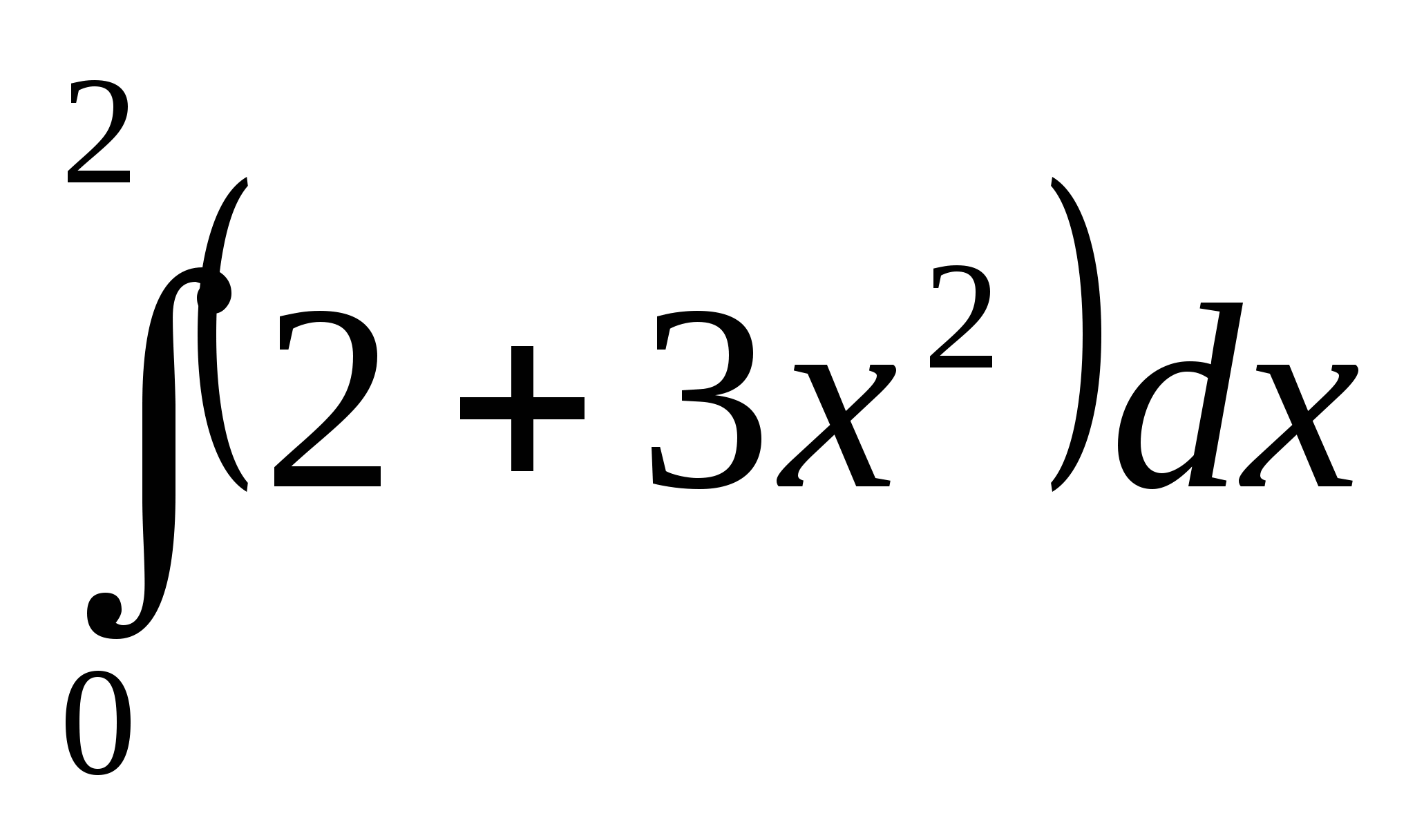

Ответ внесите в поле

10. Выберите один вариант ответа. Площадь криволинейной трапеции Д определяется интегралом:

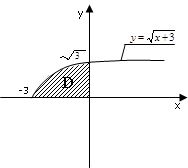
а) ;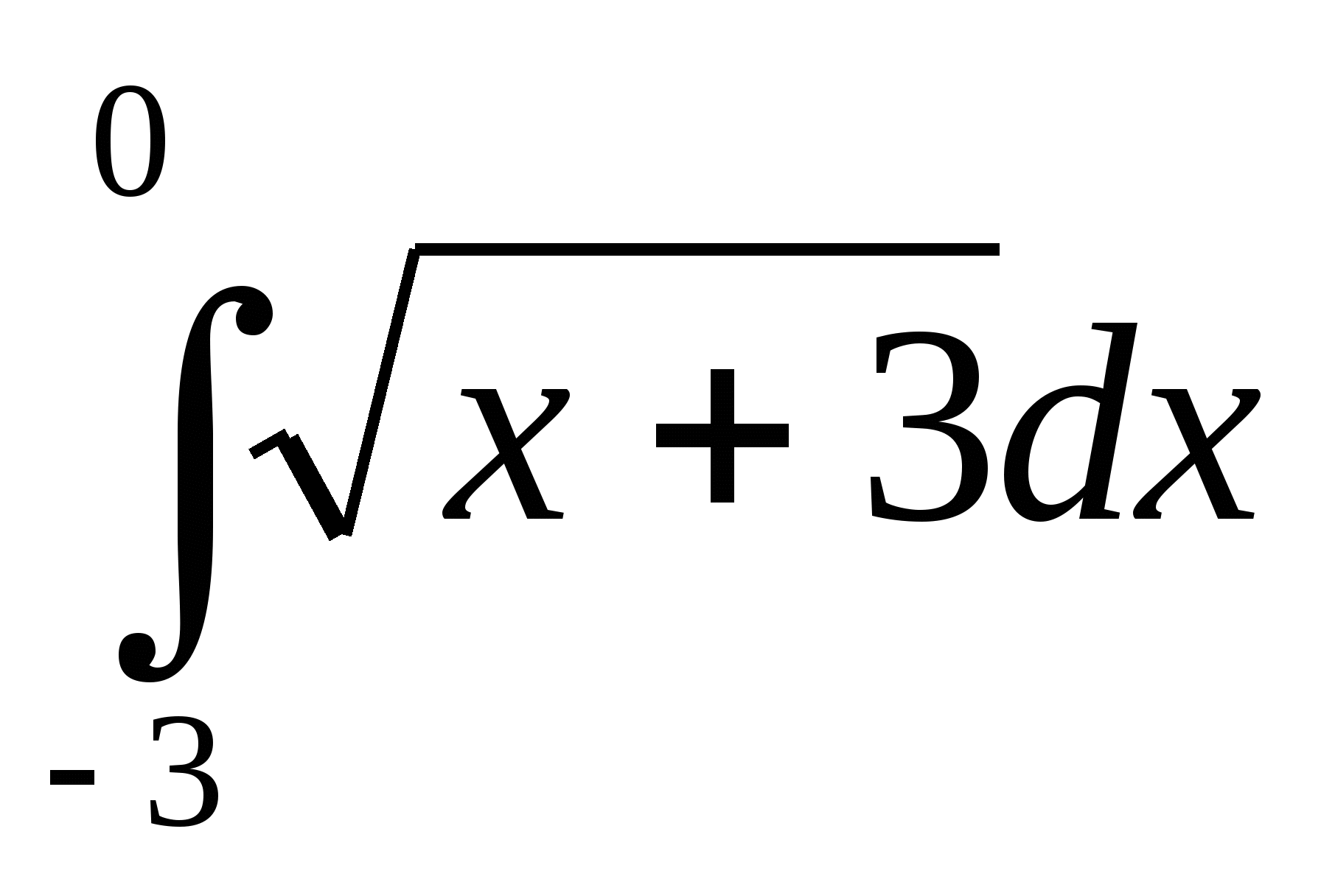

б) ;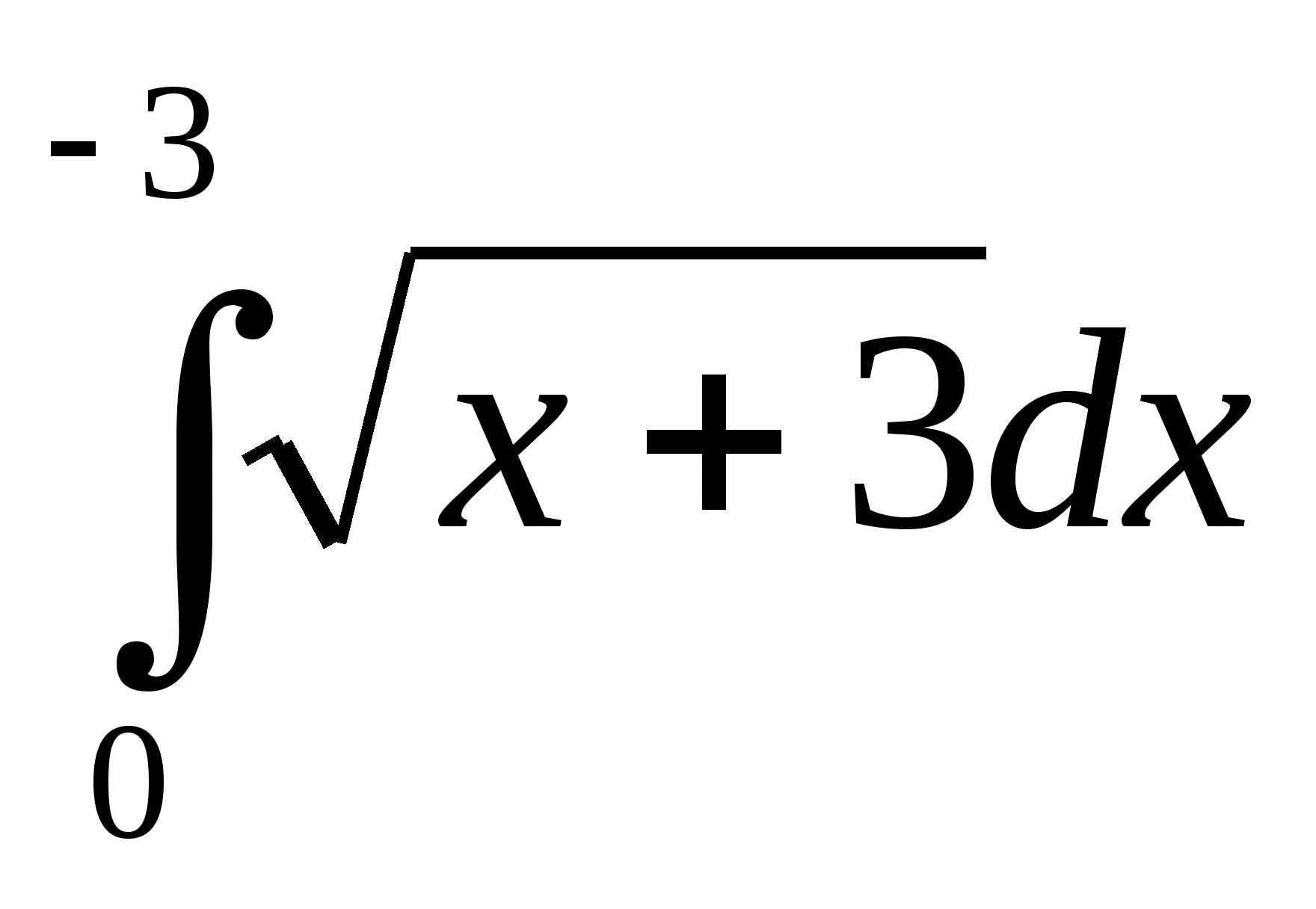

в) ;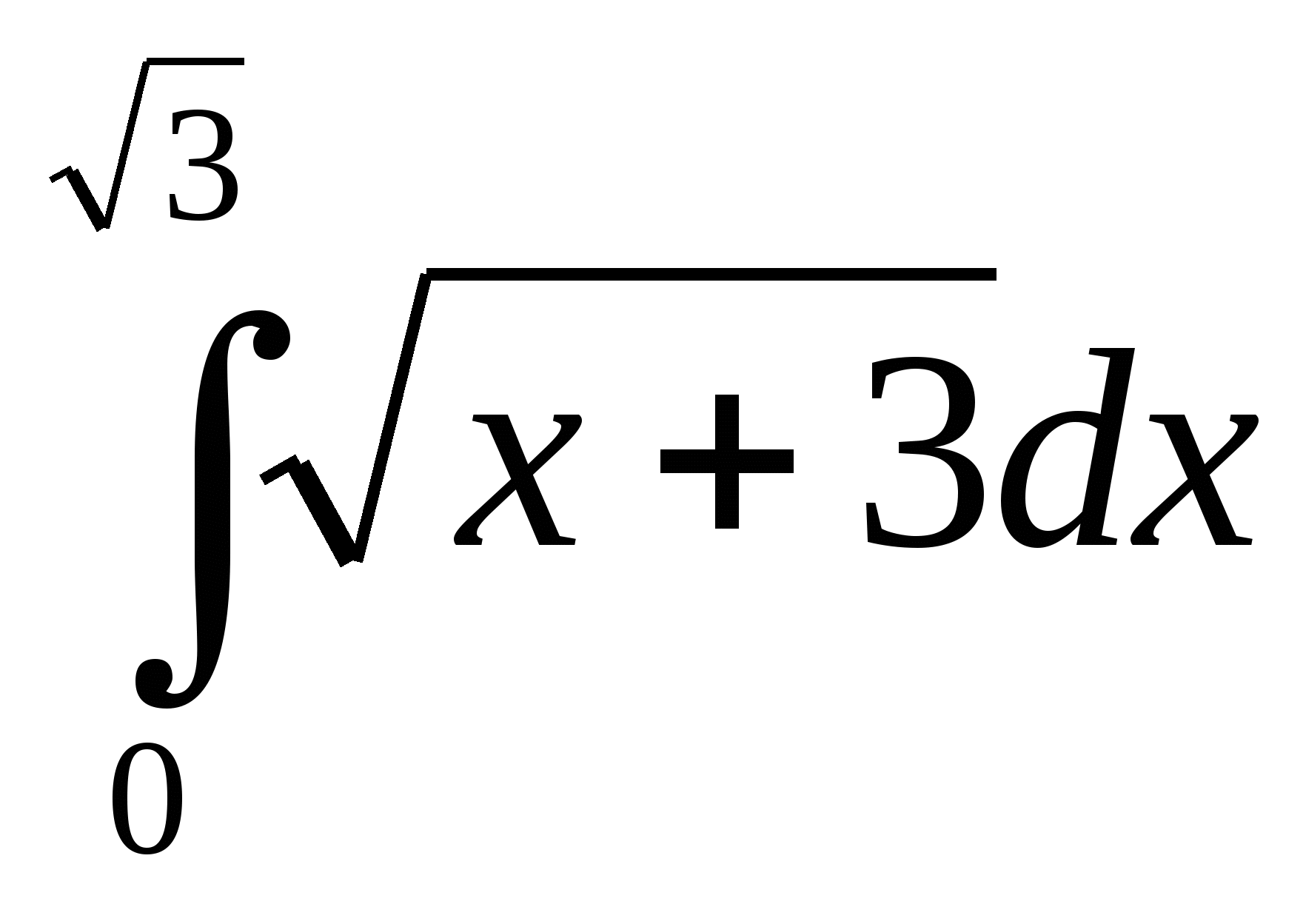

г) .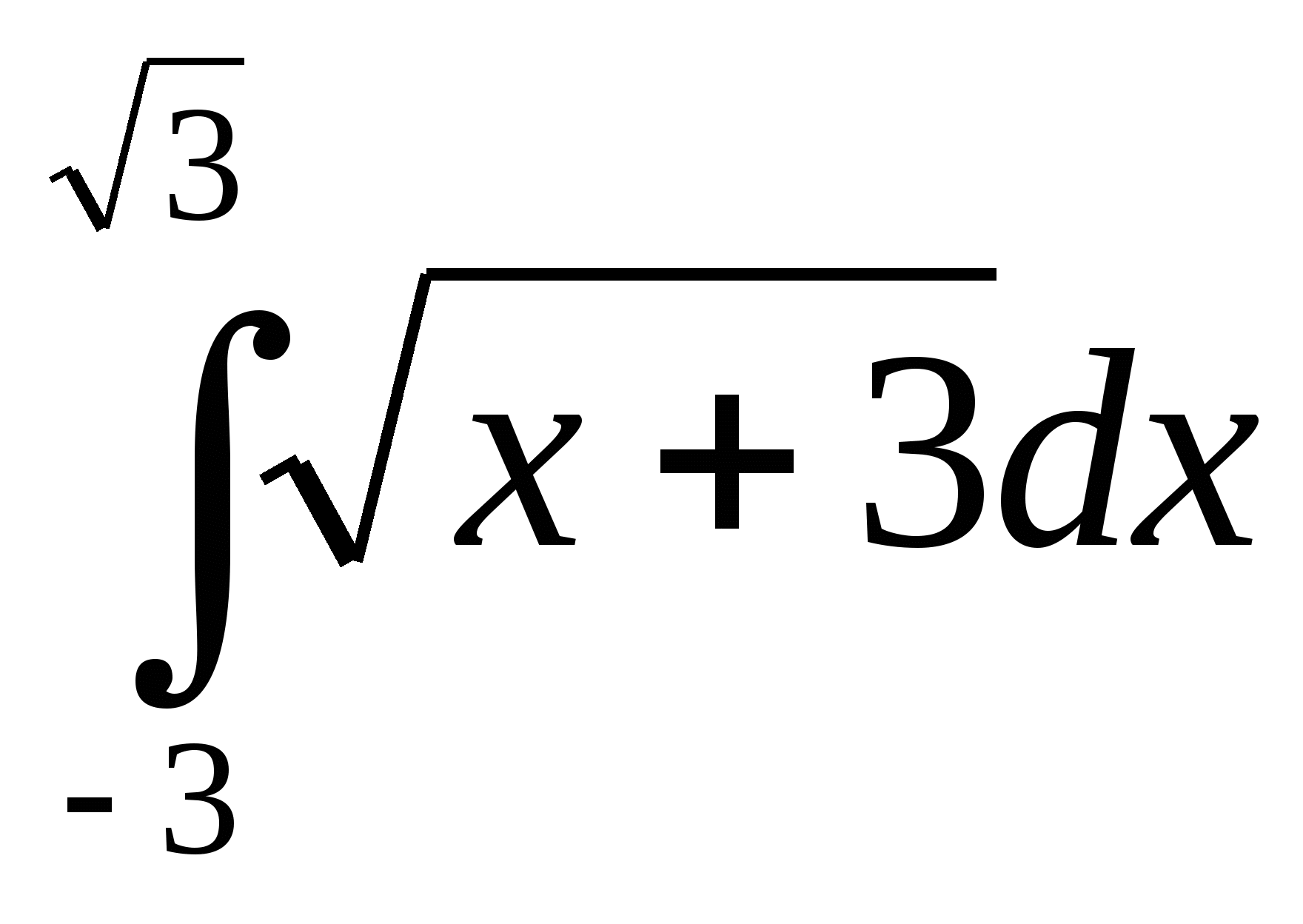

11. Скорость материальной точки, движущейся прямолинейно, равна υ (t) = 6-2t. Чему тогда равен путь, пройденный точкой от начала отсчета времени до остановки?

Ответ внесите в поле

12. В результате подстановки t = 2 - 3х, к какому виду приводится интеграл ?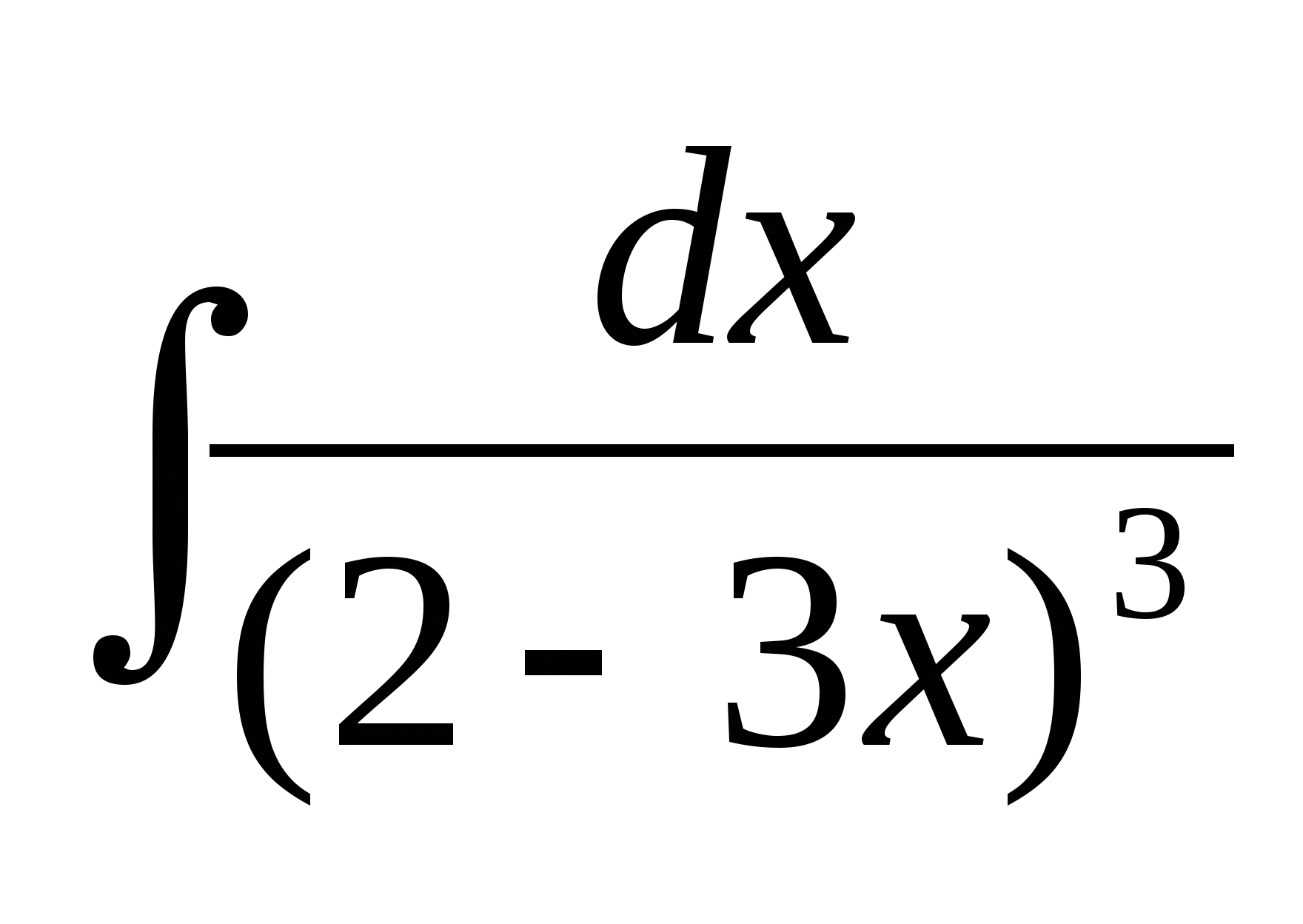

а) ;

б) ;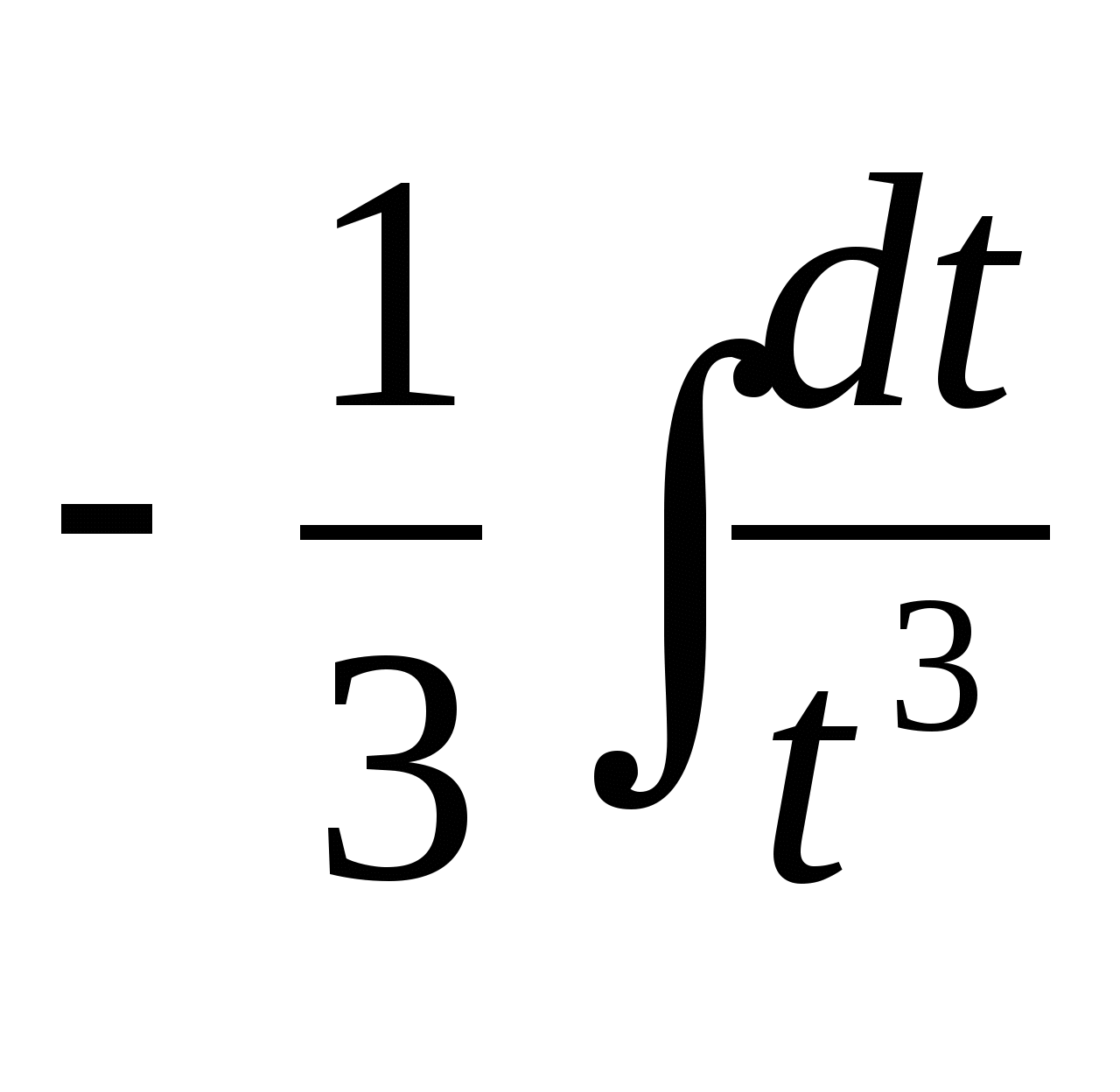

в) ;

г) .

13. Выберите один вариант ответа. Используя свойства определенного интеграла, интеграл 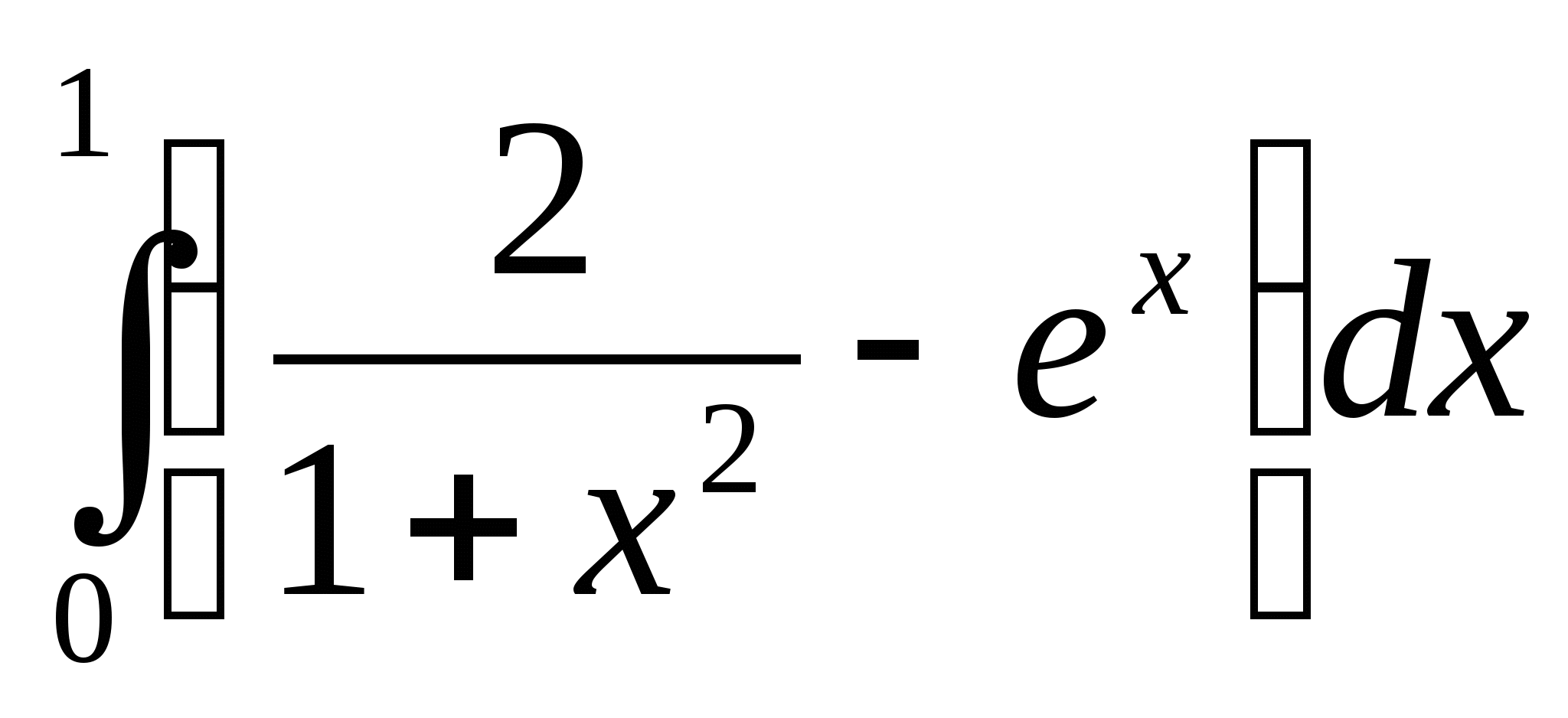можно привести к виду:

а) ;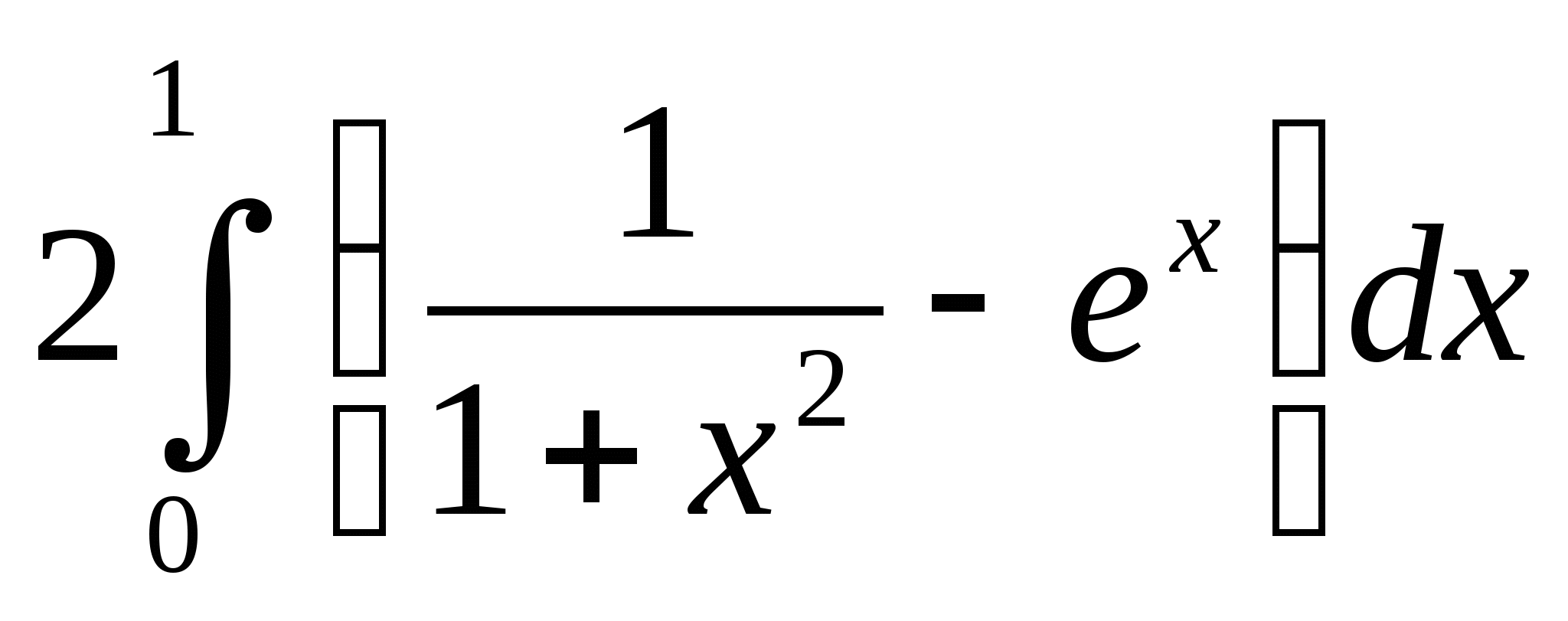

б) ;

в) ;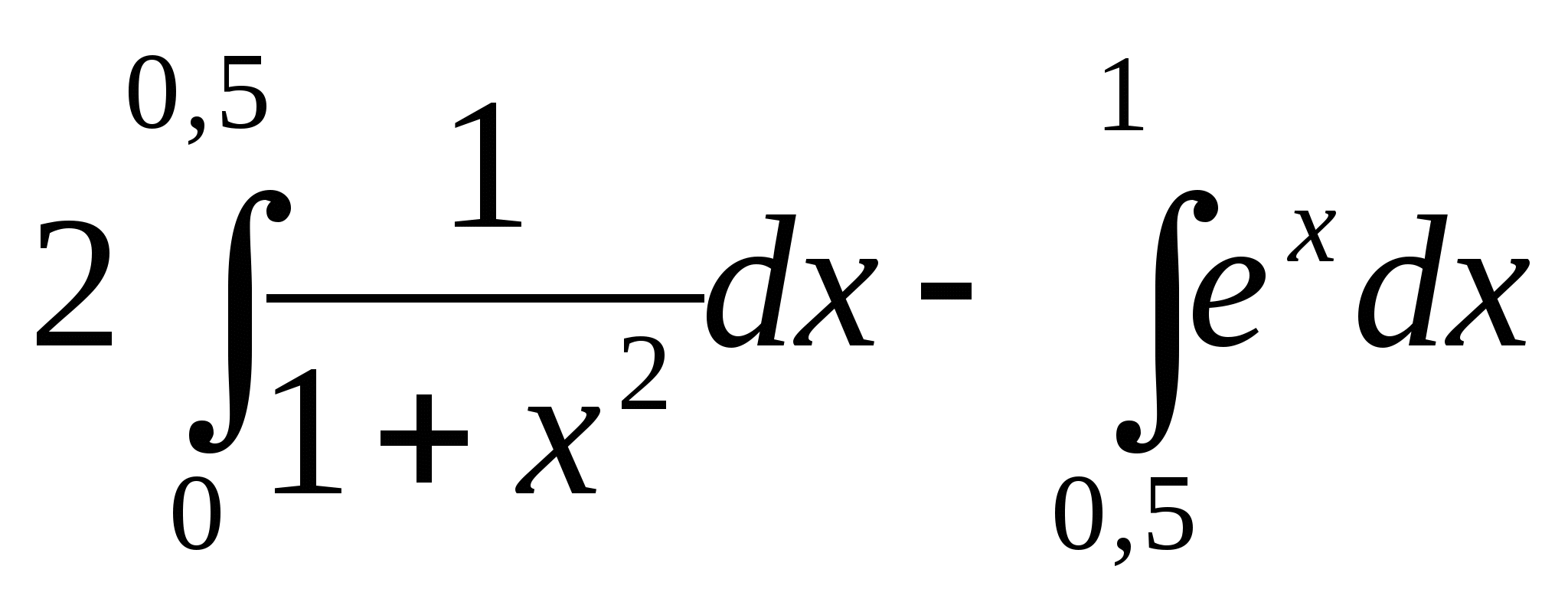

г) .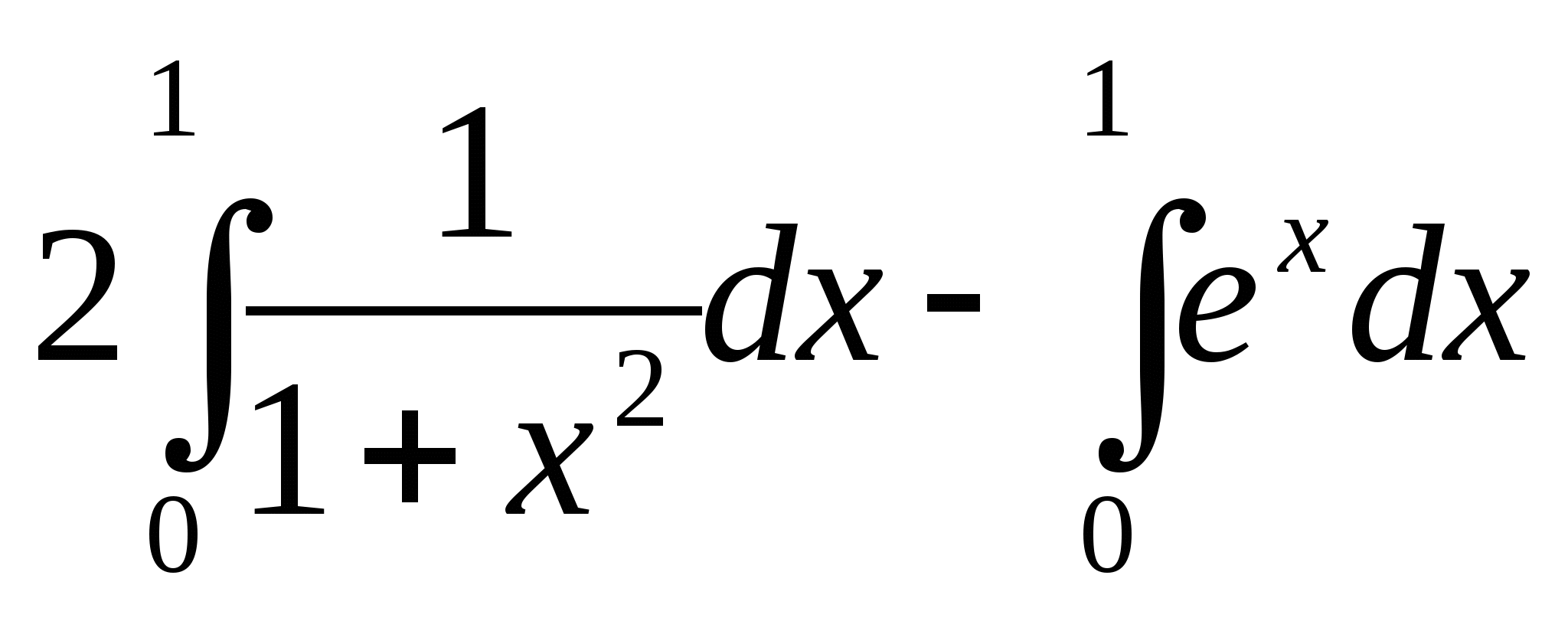

14. Выберите один вариант ответа. Область определения функции у= имеет вид:

а) ;

б) ;

в) ;

г) .

15. Выберите несколько вариантов ответа. Функция имеет разрыв в двух точках…

а) 2;

б) -2;

в) 0;

г) -3.

16. Чему равен предел ?

Ответ внесите в поле

17. Установите соответствие между пределами и их значениями.1.

а) 0

2.

б) 1

3.

в) ∞

18. Каким двум промежуткам принадлежит значение предела ?

а) [-1; 1];

б) (0; 5];

в) (-5; 0];

г) (-6; -5].

19. Два предела, значения которых равны 5.Выберите несколько вариантов ответа:

а) ;

б) ;

в) ;

г) .

20. Чему равно значение предела ?

а) е³;

б) е;

в) е^-3;

г) ∞.

21. Выберите один вариант ответа. Решением (общим интегралом) дифференциального уравнения с разделяющимися переменными 2ydy - 3x²dx = 0 является:

а) у² - х³ = с;

б) 2у² - 3х³ = с;

в) 2у - 3х² = с;

г) у² = х³.

22. Вычислите приблизительное значение корня из перечисленных вариантов ответов:

а) 1;

б) 1,004;

в) 1,04;

г) 1,039.

Вариант №2

1. Площадь криволинейной трапеции Д определяется интегралом:

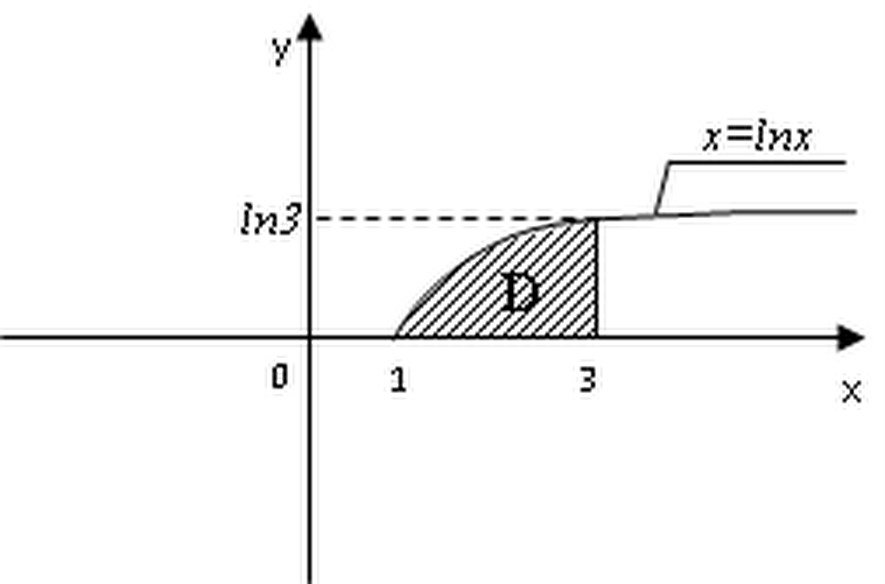
а) ;

б) ;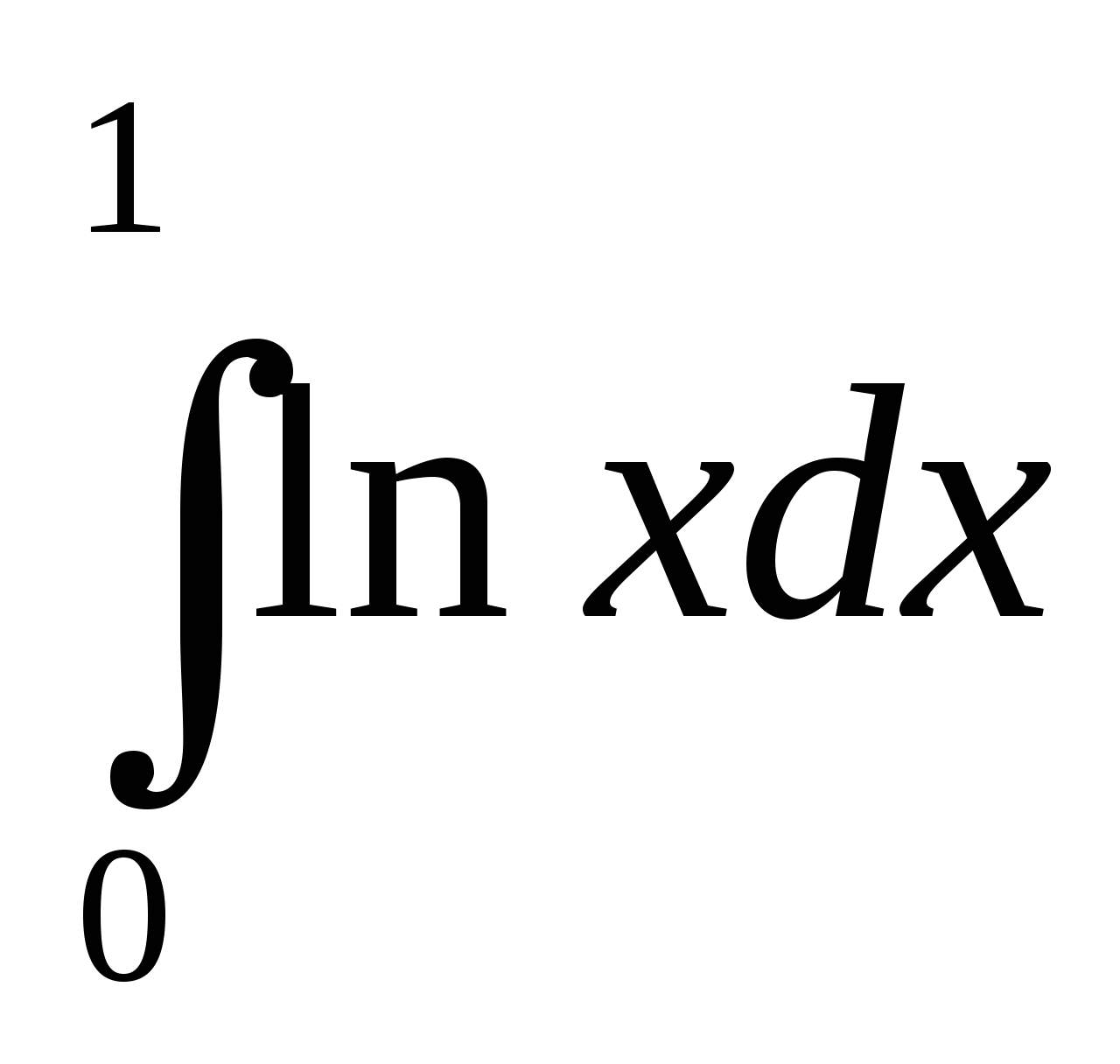

в) ;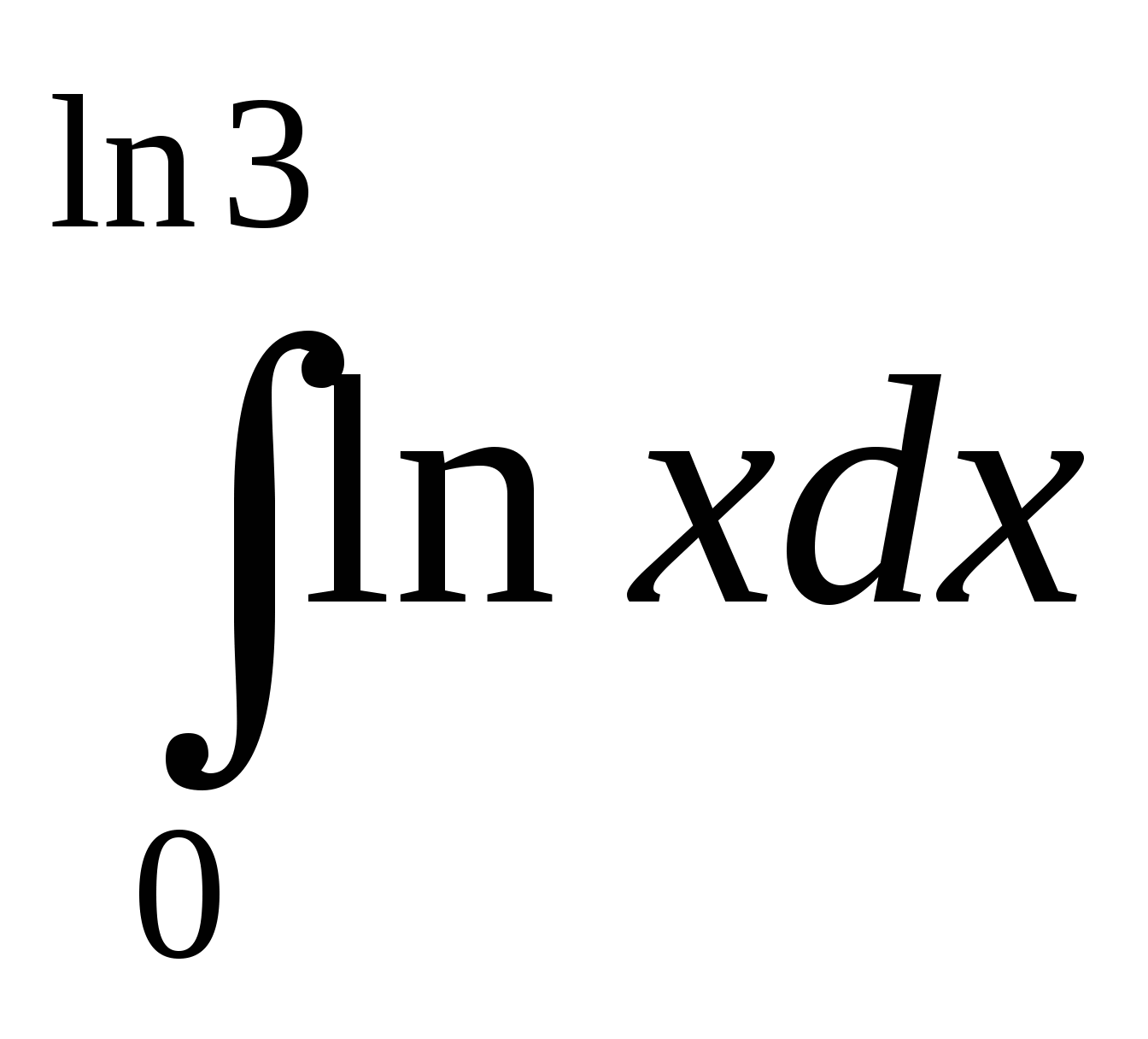

г) .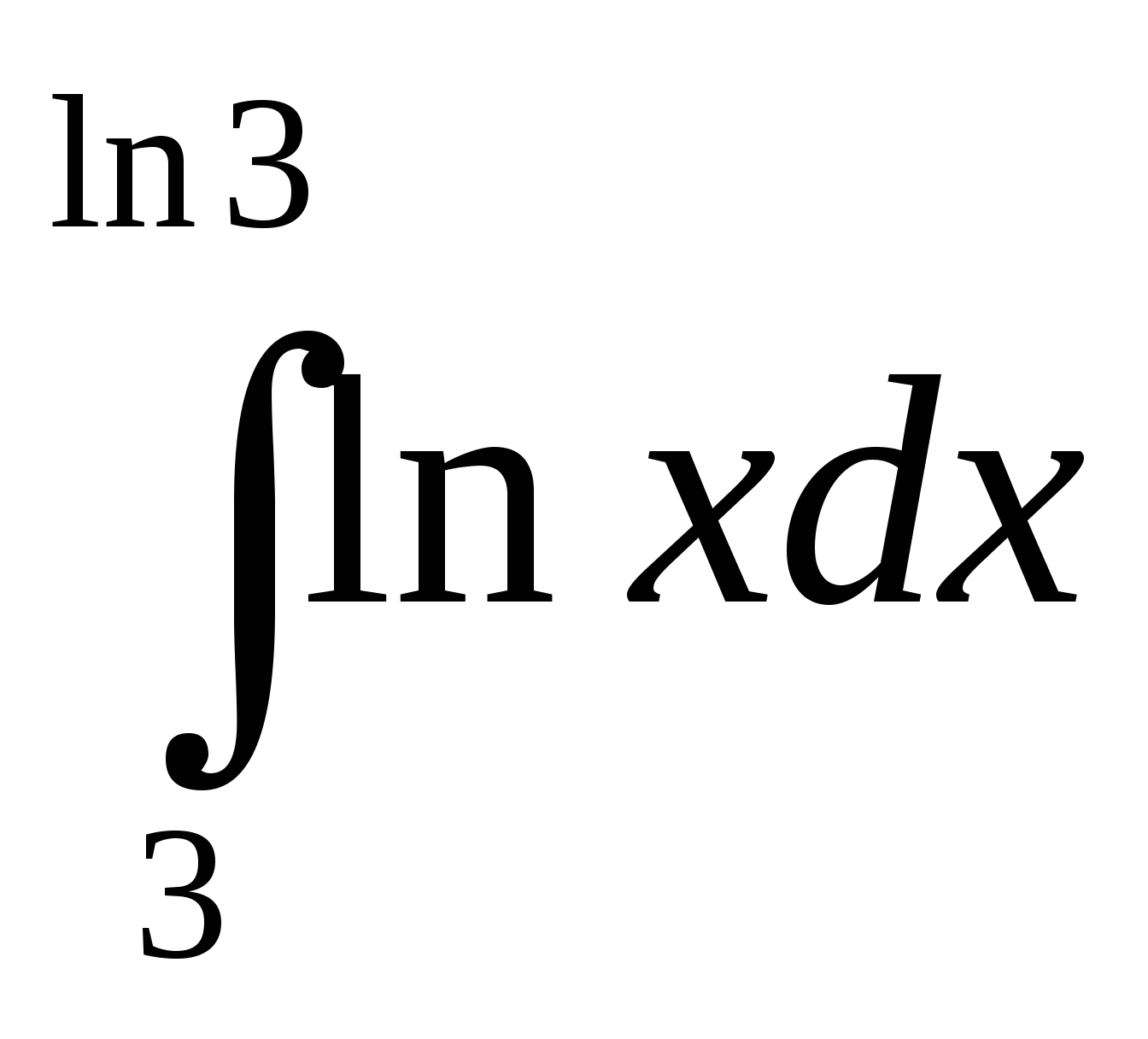

2. В результате подстановки t = 5х + 2 интеграл 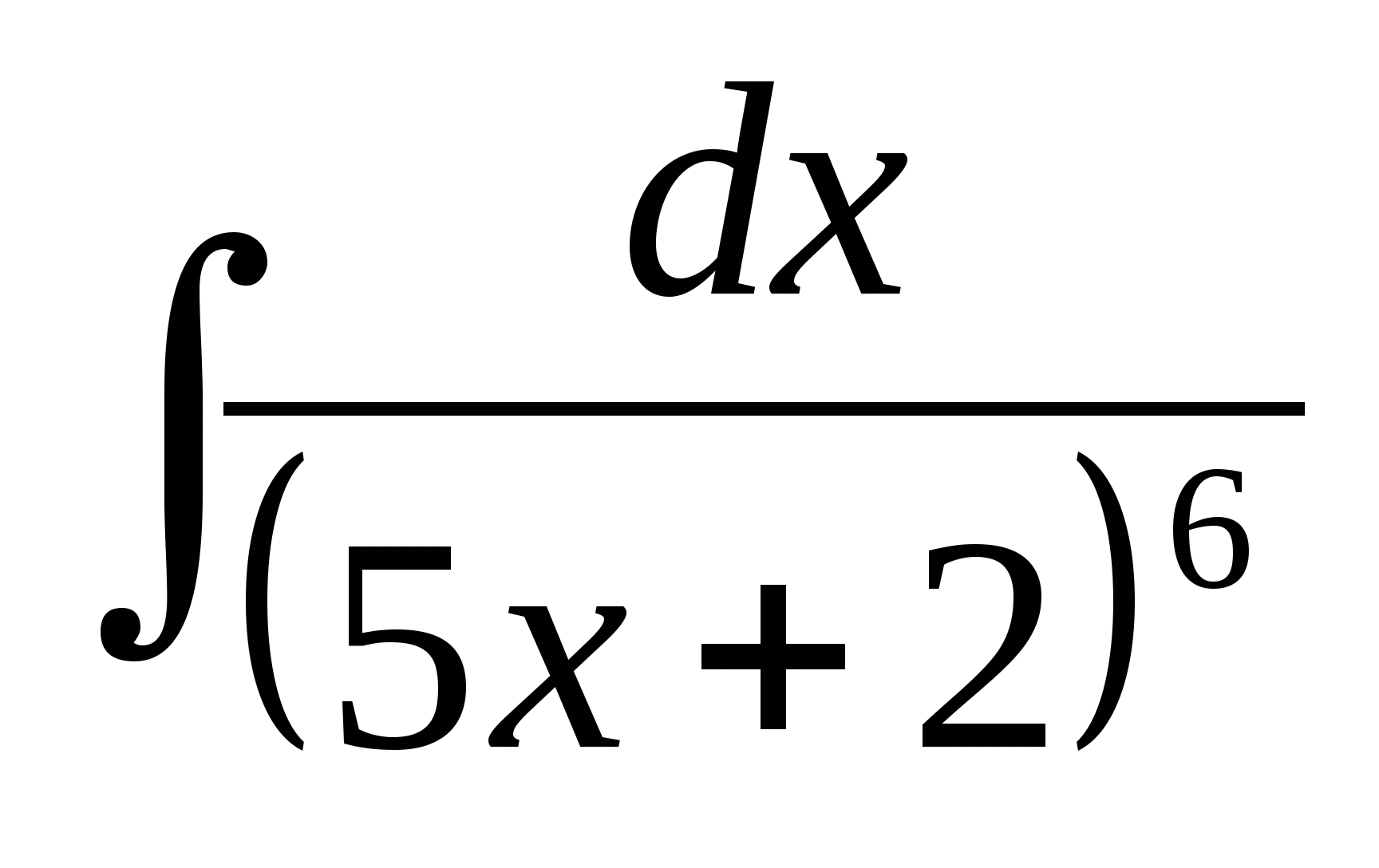приводится к виду:

а) ;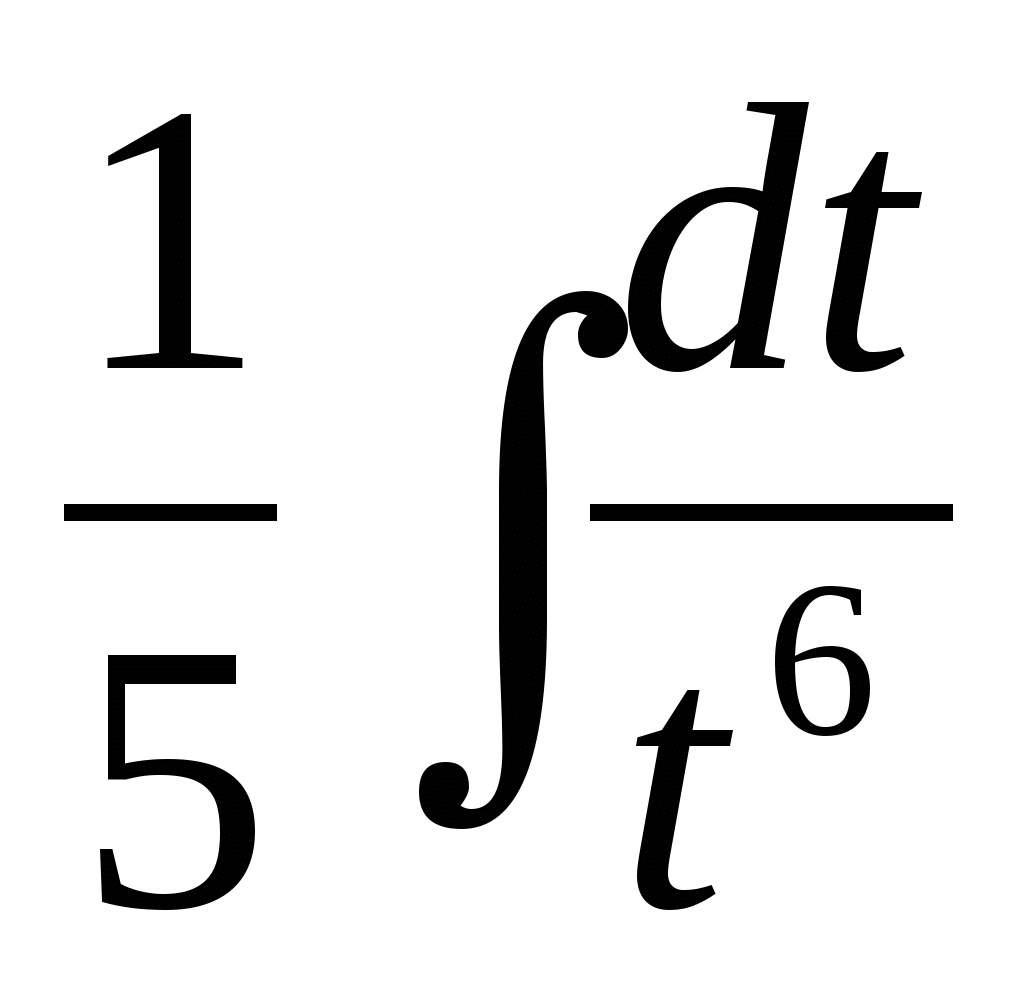

б) ;

в) ;

г) .

3. Множество всех первообразных функций у = 3х² имеет вид:

а) х³ + с;

б) х³;

в) 6х;

г) 3х³ + с.

4. Используя свойства определенного интеграла, интеграл 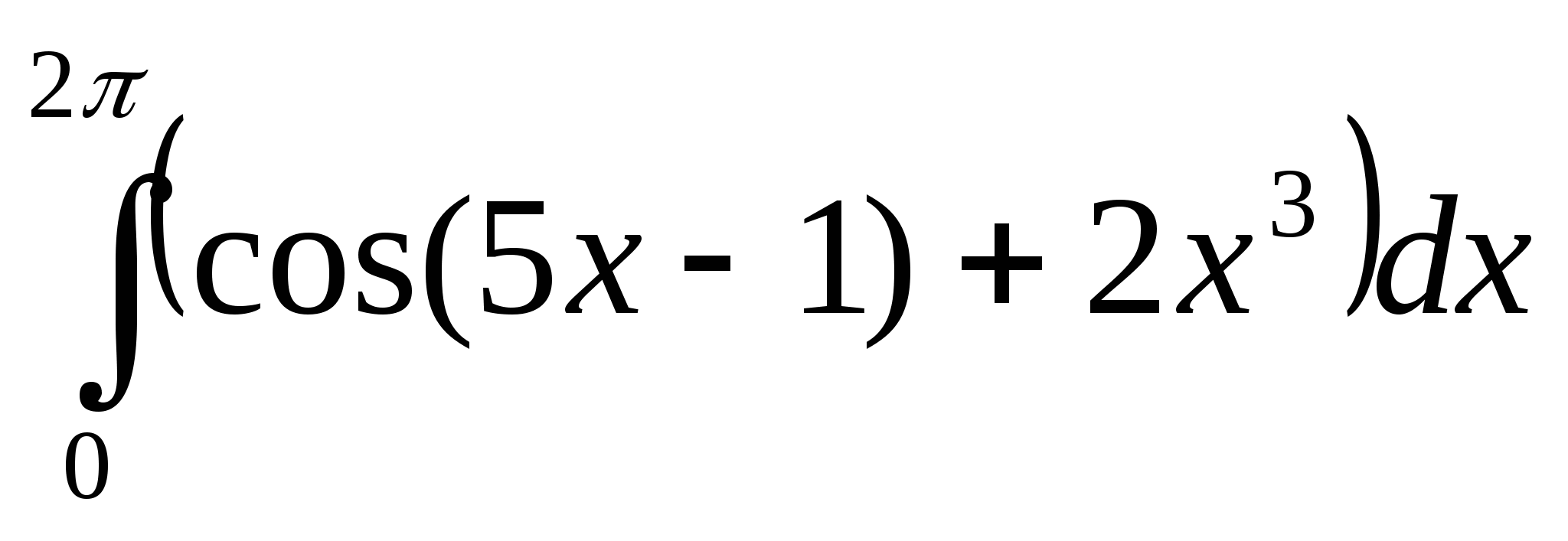можно привести к виду:

а) ;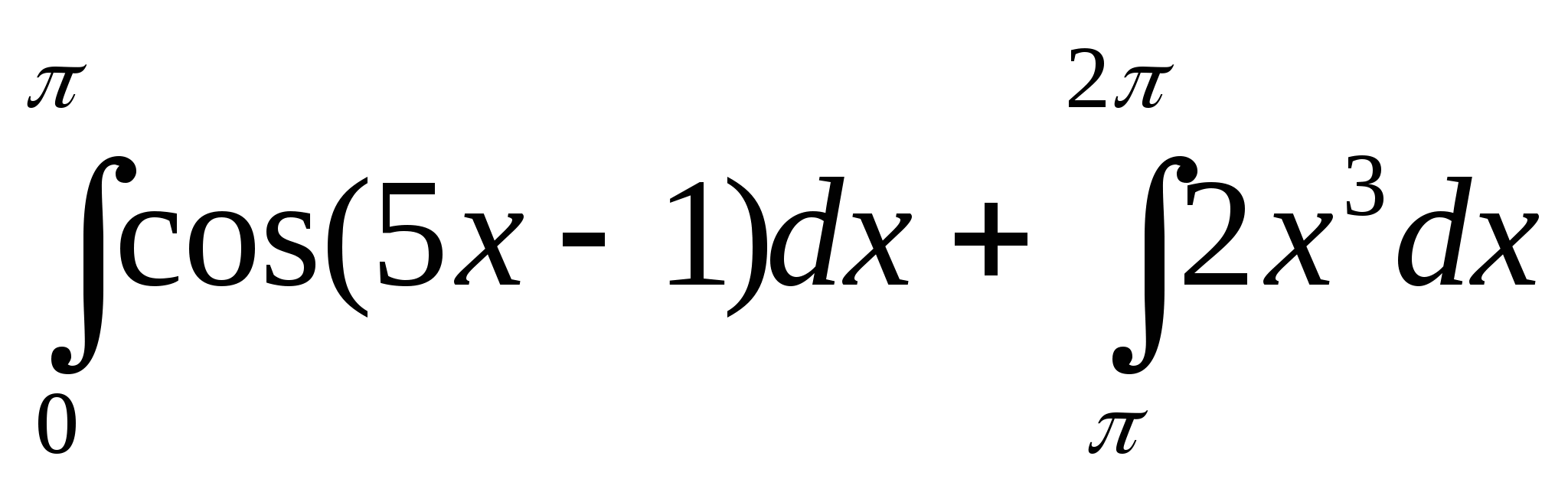

б) ;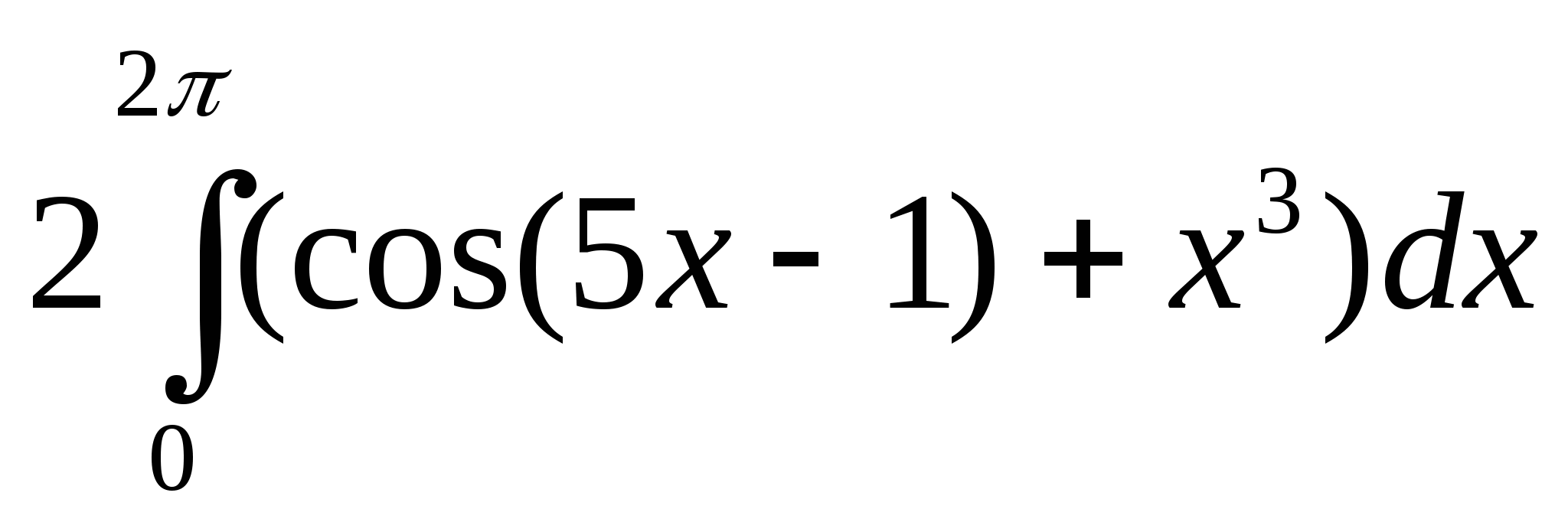

в) ;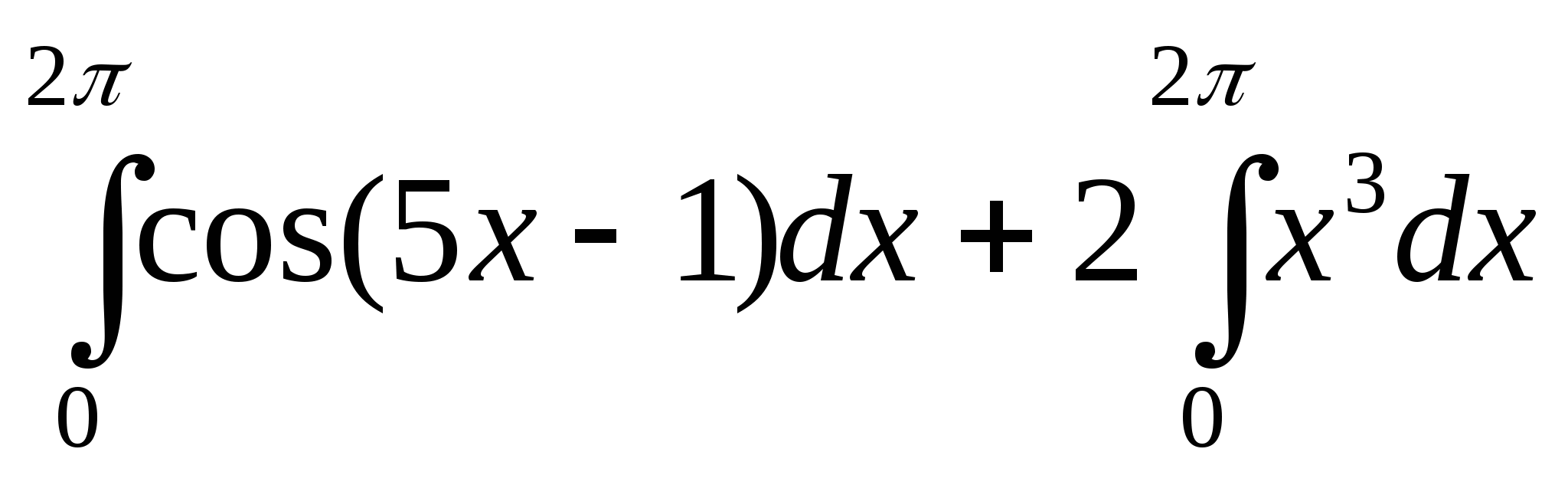

г) .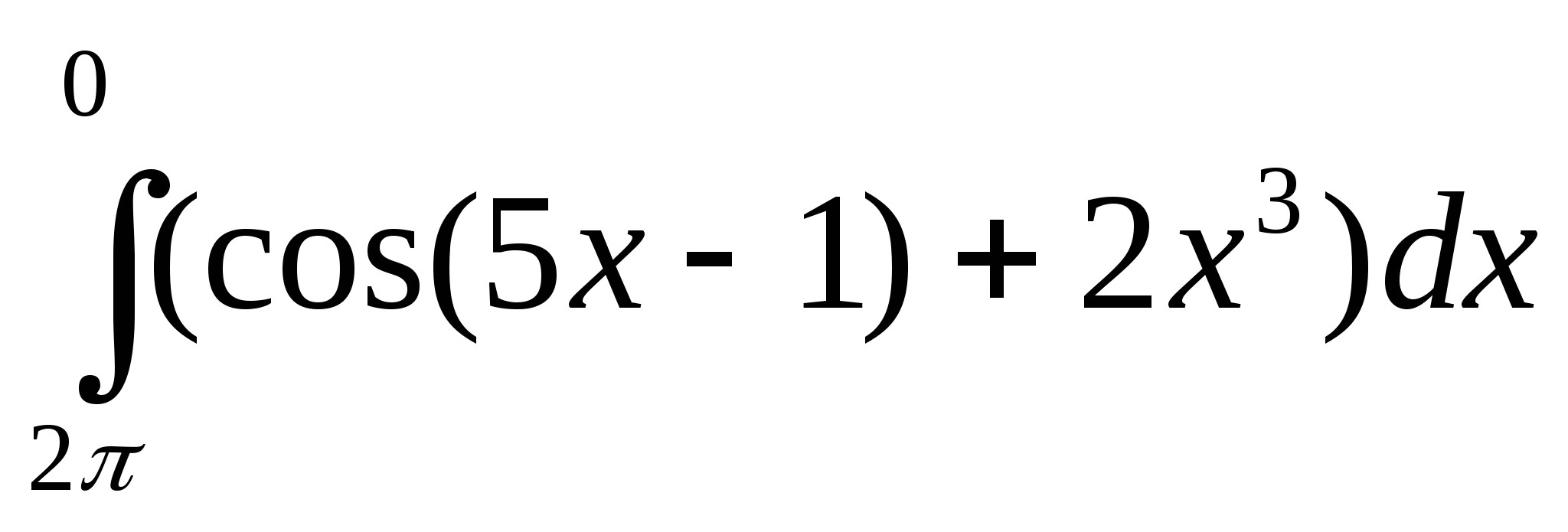

5. Скорость материальной точки, движущейся прямолинейно, равна υ (t) = 2 - t. Чему будет равен путь, пройденный точкой от начала отсчета времени до остановки?

Ответ внесите в поле

6. Чему равен интеграл ?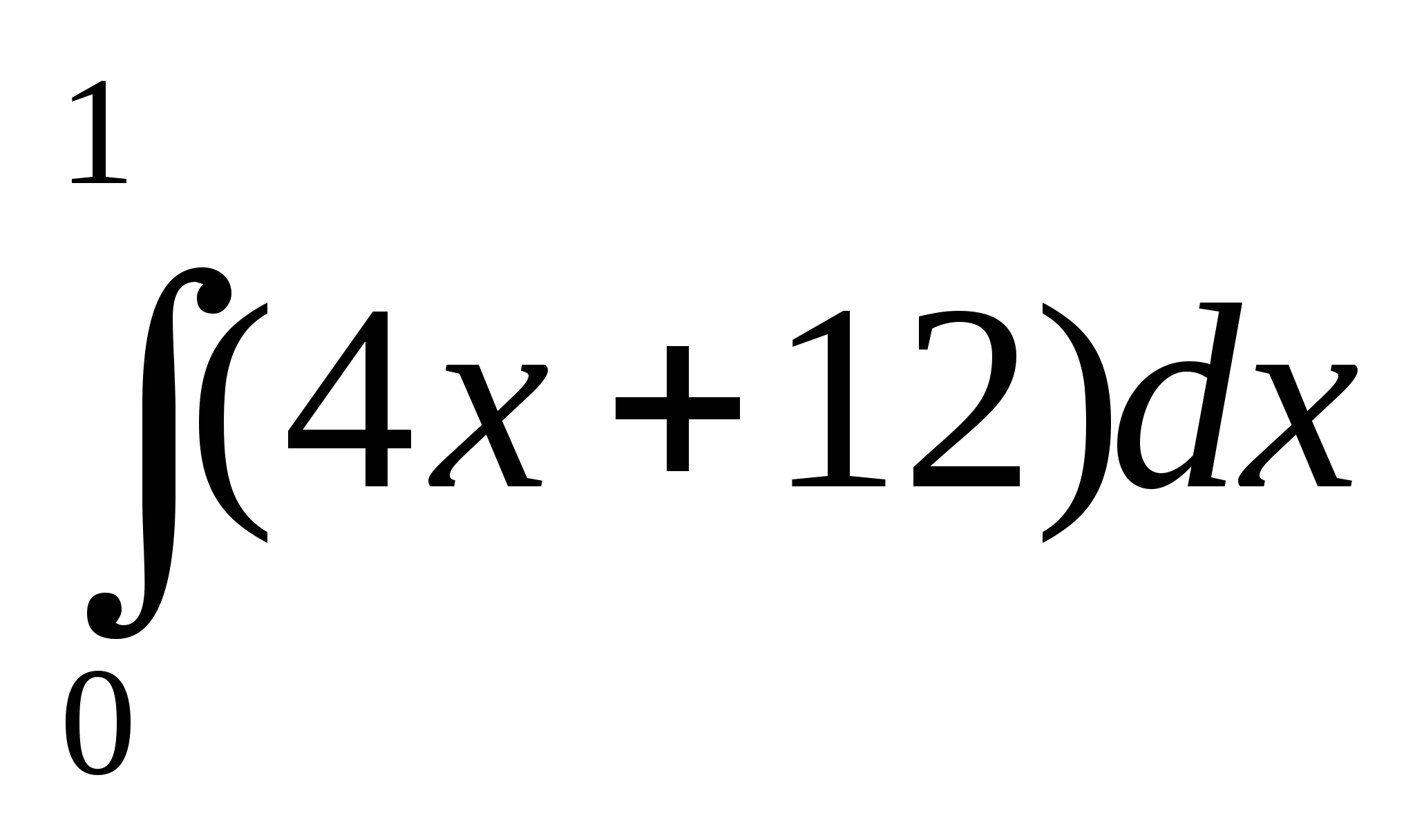

Ответ внесите в поле

7. Какой вид имеет производная функции у = х·сos x? Выберете правильный ответ.

а) у' = cos x - x sin x;

б) у' = cos x + x sin x;

в) у' = 1 - sin x;

г) у' = - sin x.

8. Абсциссой точки перегиба графика функции у = 5 - +3 х² является:

а) 3;

б) 0;

в) 2;

г) -2.

9. Дана функция у = х³ - 2х² + 5. Установите соответствие между производными функции в соответствующих точках и их значениями:у' (-1)

у' (1)

у' (2)

а) 4;

б) 7;

в) -1.

10. Чему равна производная функции y = 6 arccos x в точке х_о = 0?

а) 0;

б) 6;

в) -6;

г) .

11. Установите соответствие между функциями и их производными:;

;

.

а) f'(x) = ;

б) f'(x) = ;

в) f'(x) = .

12. Чему равна вторая производная функции f'(x) = 9х² - 14?

Ответ внесите в поле

13. Расположите функции, определенные на всей числовой прямой, знаки производных которых указаны на рисунках по возрастанию количества точек максимума.а)

f '(х)

+

+

+

+

+

+

>

-1

0

2

4

6

х

б)

f '(х)

-

+

-

+

-

-

>

-1

0

2

4

6

х

в)

f '(х)

+

-

-

-

-

-

>

-1

0

2

4

6

х

г)

f '(х)

+

-

+

-

+

-

>

-1

0

2

4

6

х

14. Чему равен угловой коэффициент касательной к графику функции у = 3 - 2х - х² в точке х_о = 1?

а) - 4;

б) 0;

в) 4;

г) - 1.

15. Вычислите значение предела .

а) ;

б) 0;

в) ;

г) .

16.Найдите два предела, значение которых равны 10.

а) ;

б) ;

в) ;

г) .

17. Какой вид имеет область определения функции ?

а) ;

б) ;

в) ;

г) .

18. В каких двух точках, функция имеет разрыв?

а) 0;

б) - 4;

в) 1;

г) - 1.

19. Значение, равное 8, имеют два из приведенных ниже предела:

а) ;

б) ;

в) ;

г) .

20. Чему равен предел ?

Ответ внесите в поле

21. Частными решениями дифференциального уравнения у'' - 3у' - 4у = 0 являются (выберите два и более вариантов ответа):

а) у = 2е^-х;

б) у = е^4х;

в) у = sin х;

г) у = х² - 3х - 4.

22. Вычислите приближенное значение степени (1,02)⁵.

а) 1;

б) 2;

в) 1,1;

г) 1,045.

Вариант №3

1. Установите соответствие между производными функции у = 2х⁴- 3х - 5 в соответствующих точках и их значениями.у' (-1)

у' (1)

у' (0)

а) -11

б) - 3

в) 5

2. Укажите две функции, определенные на всей числовой прямой и имеющие точку перегиба х_о = 1. Знаки производных второго порядка указаны на рисунках.а)

f ''(х)

-

-

+

-

>

-1

0

1

х

б)

f ''(х)

-

+

-

-

>

-1

0

1

х

в)

f ''(х)

-

-

+

+

>

-1

0

1

х

г)

f ''(х)

-

-

-

+

>

-1

0

1

х

3. Производная функции y = arcctg x+arcsin x в точке х₀ = 0 равна:

а) 2;

б) 1;

в) -2;

г) 0.

4. Чему равна вторая производная функции f (х) = 5х+x²?

Ответ внесите в поле

5. Установите соответствие между функциями и их производными:f (х) = (3х+1)³

f (х) = (3х+1)²

f (х) = (2х+1)³

а) f '(х) = 9 (3х+1)²

б) f '(х) = 6 (3х+1)

в) f '(х) = 6 (2х+1)²

6. На рисунке представлен график производной функции y = f '(х)

Выберете правильный вариант ответа:

а) х = 0 - точка максимума;

б) х = - 3 - точка минимума;

в) х = 3 - точка минимума;

г) х = - 3 - точка максимума.

7. Установите соответствие между функциями и их производными:f (х) = 6+cos x

f (х) = 6х+cos x

f (х) = 6 -cos x

а) f '(х) = sin x

б) f '(х) = 6-sin x

в) f '(х) = - sin x

8. Предел равен…..

Ответ внесите в поле

9. Значение предела равно:

а) е;

б) ∞;

в) е³;

г) е^-3.

10. Значение предела принадлежит двум промежуткам:

а) (0; 5];

б) [-1; 1];

в) (-6; -5];

г) (-5; 0].

11. Установите соответствие между пределами и их значениями.1.

а) 1

2.

б) ∞

3.

в) 0

12. Найдите два предела, значения которых равны 5:

а) ;

б) ;

в) ;

г) .

13. Область определения функции у= имеет вид:

а) ;

б) ;

в) ;

г) .

14. Решением (общим интегралом) дифференциального уравнения с разделяющимися переменными 2ydy - 3x²dx = 0 является:

а) 2у² - 3х³ = С;

б) у² = х³;

в) у² - х³ = С;

г) 2у - 3х² = С.

15. Функция имеет разрыв в двух точках:

а) -2;

б) 0;

в) -3;

г) 2.

16. Вычислите приблизительное значение корня из перечисленных вариантов ответов:

а) 1,004;

б) 1,04;

в) 1,039;

г) 1.

17. Выберите один вариант ответа. Используя свойства определенного интеграла, интеграл 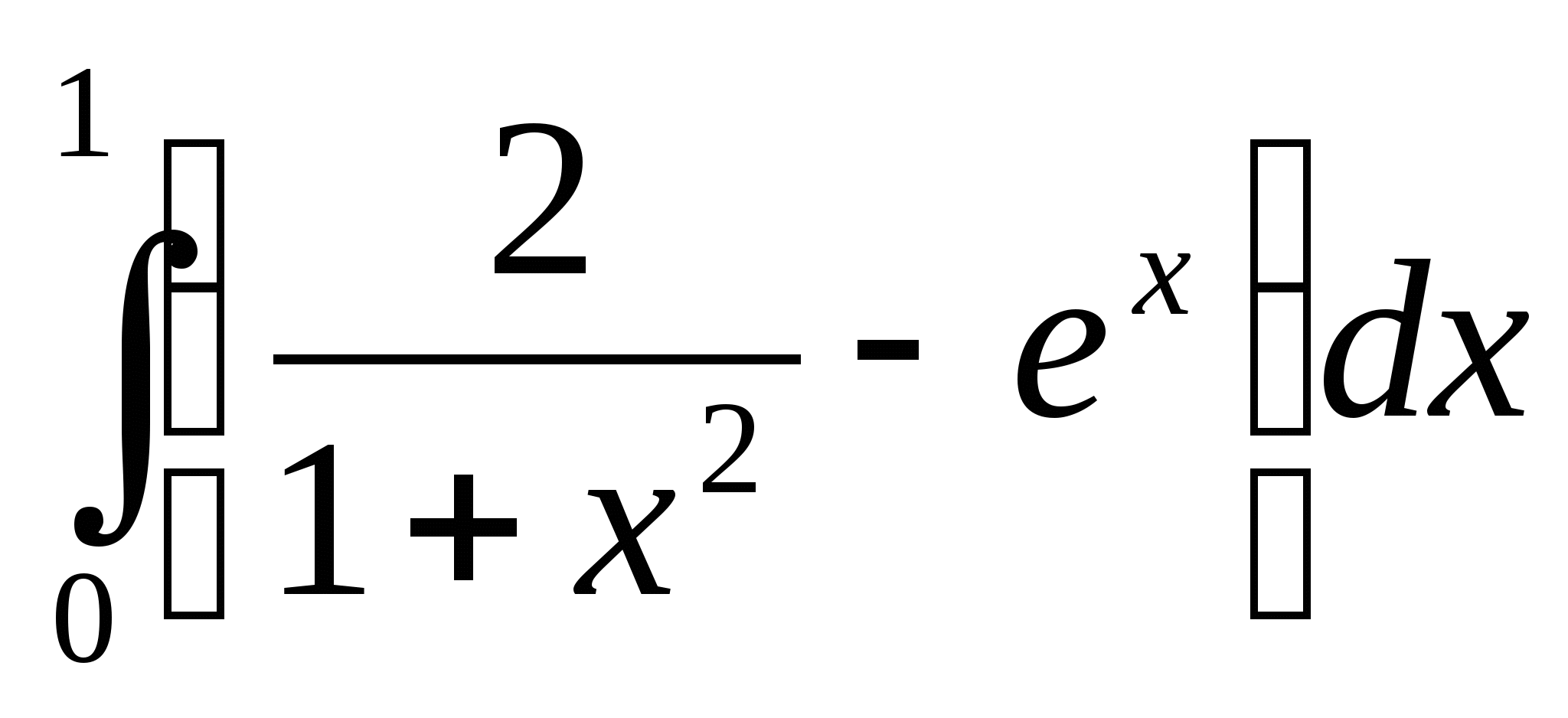можно привести к виду:

а) ;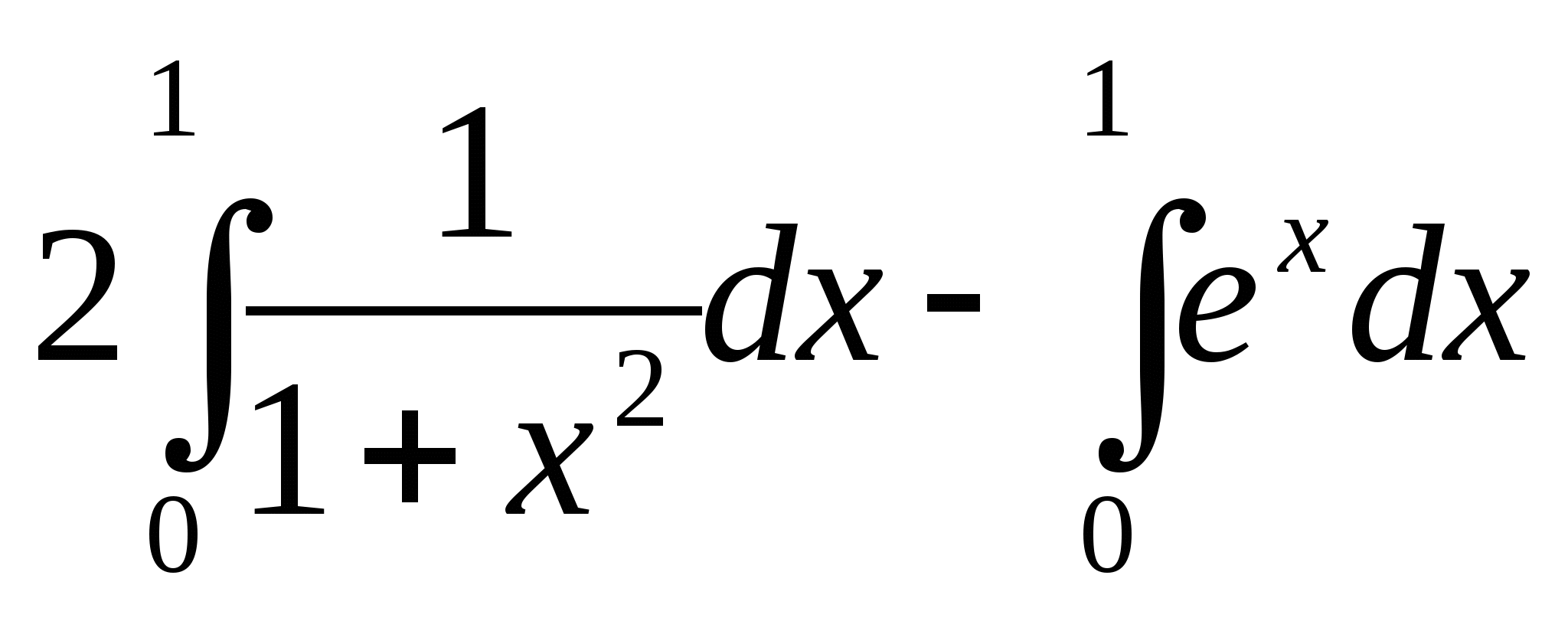

б) ;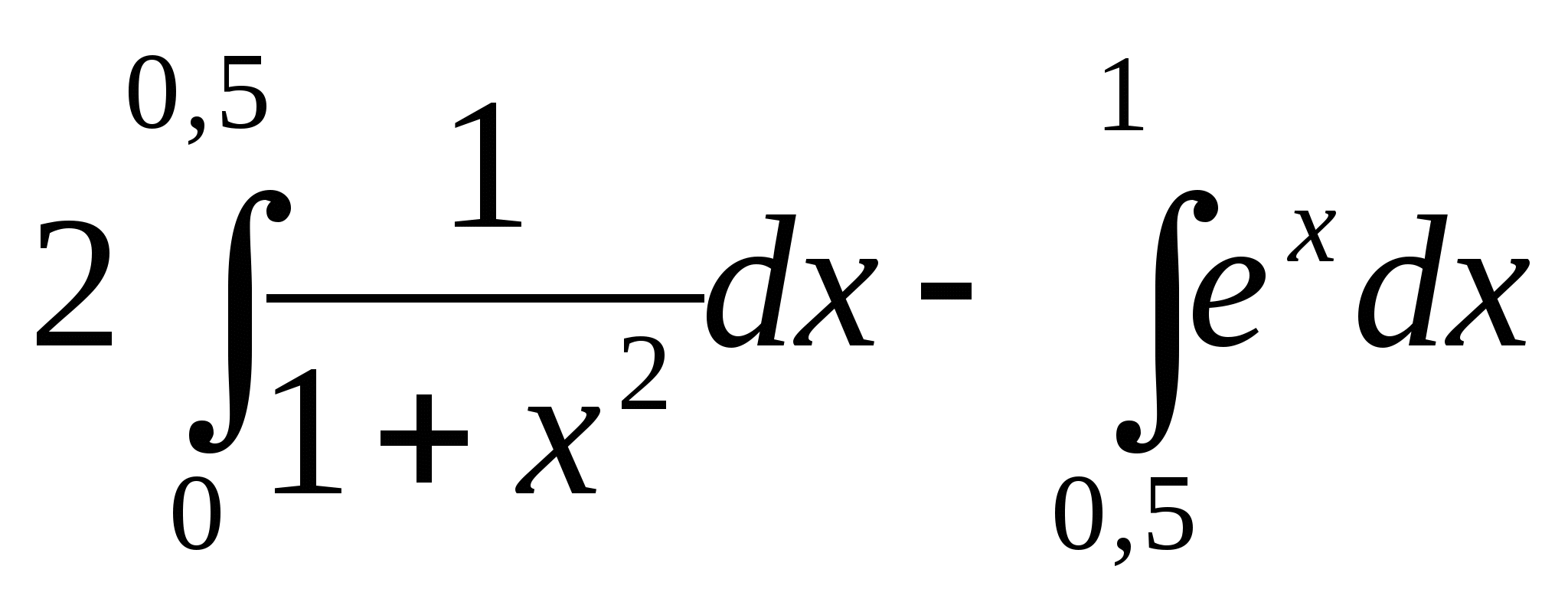

в) ;

г) .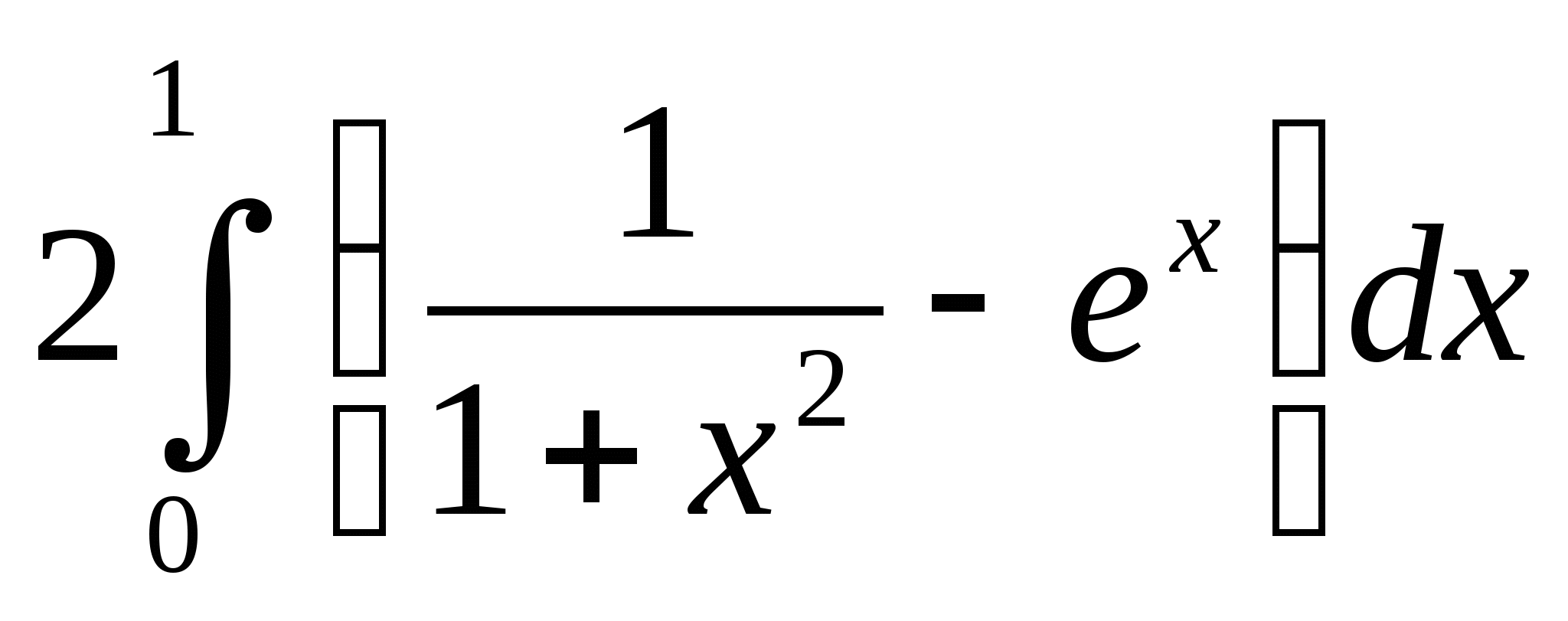

18. Выберите один вариант ответа. Площадь криволинейной трапеции Д определяется интегралом:

а) ;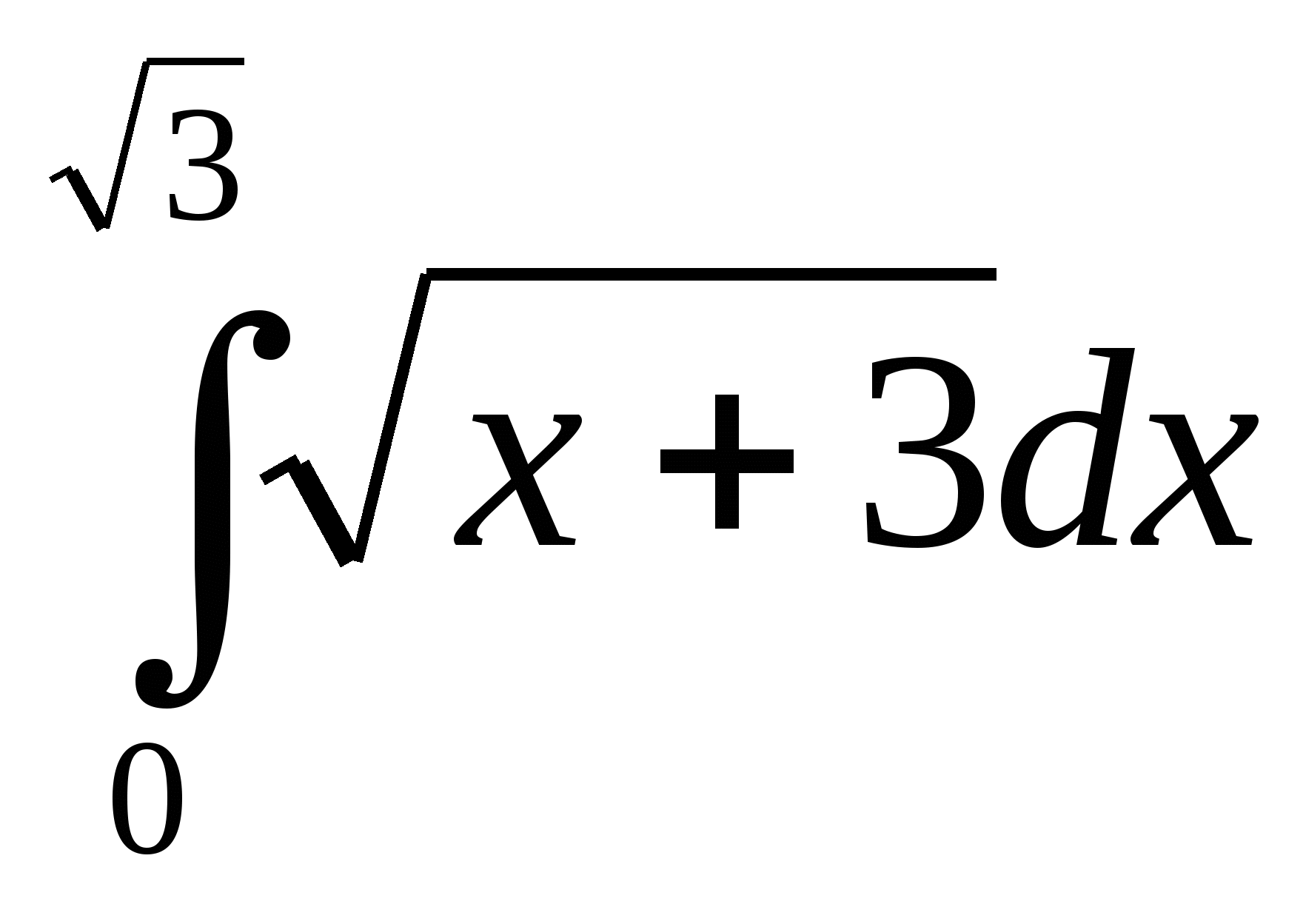

б) .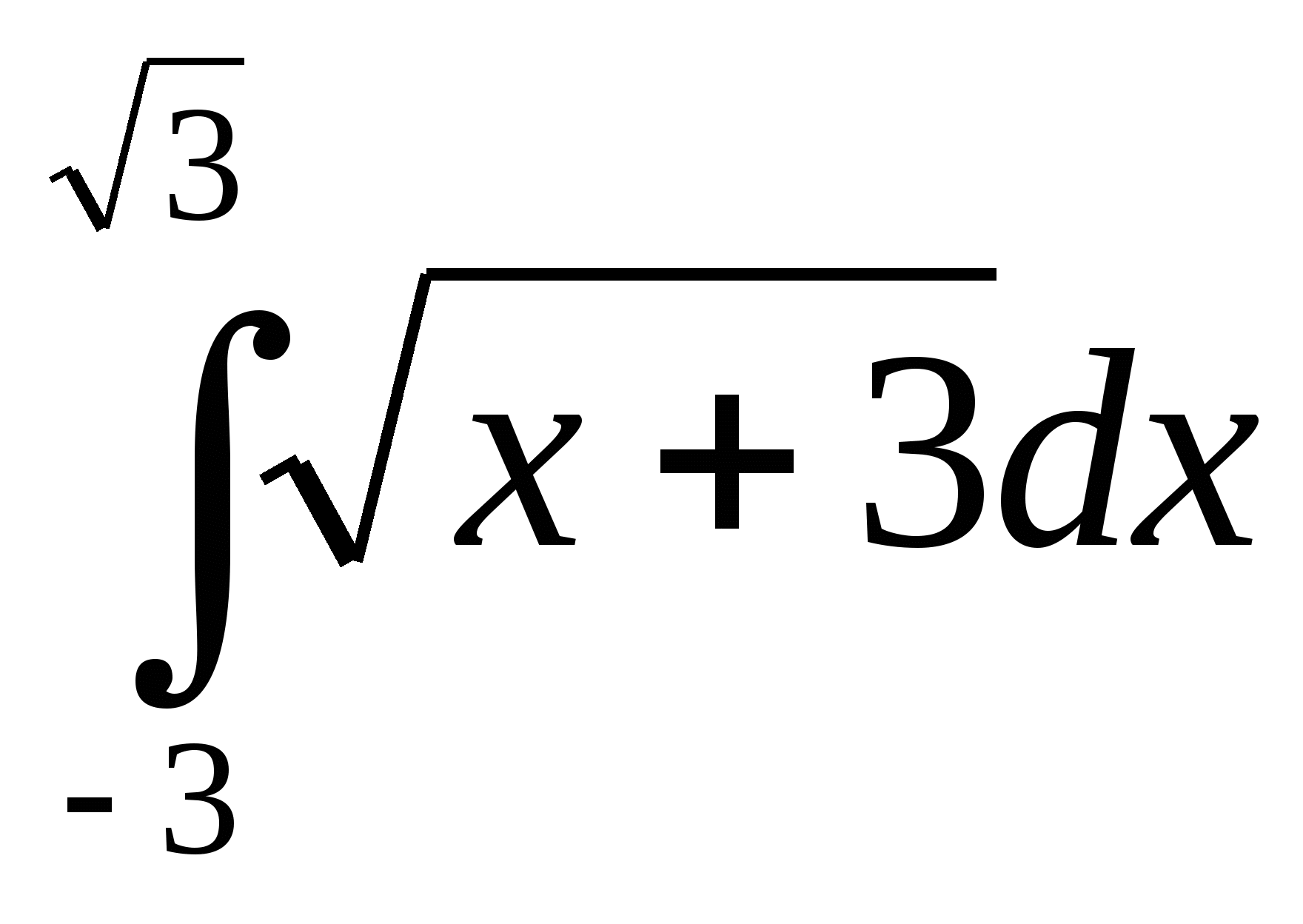

в) ;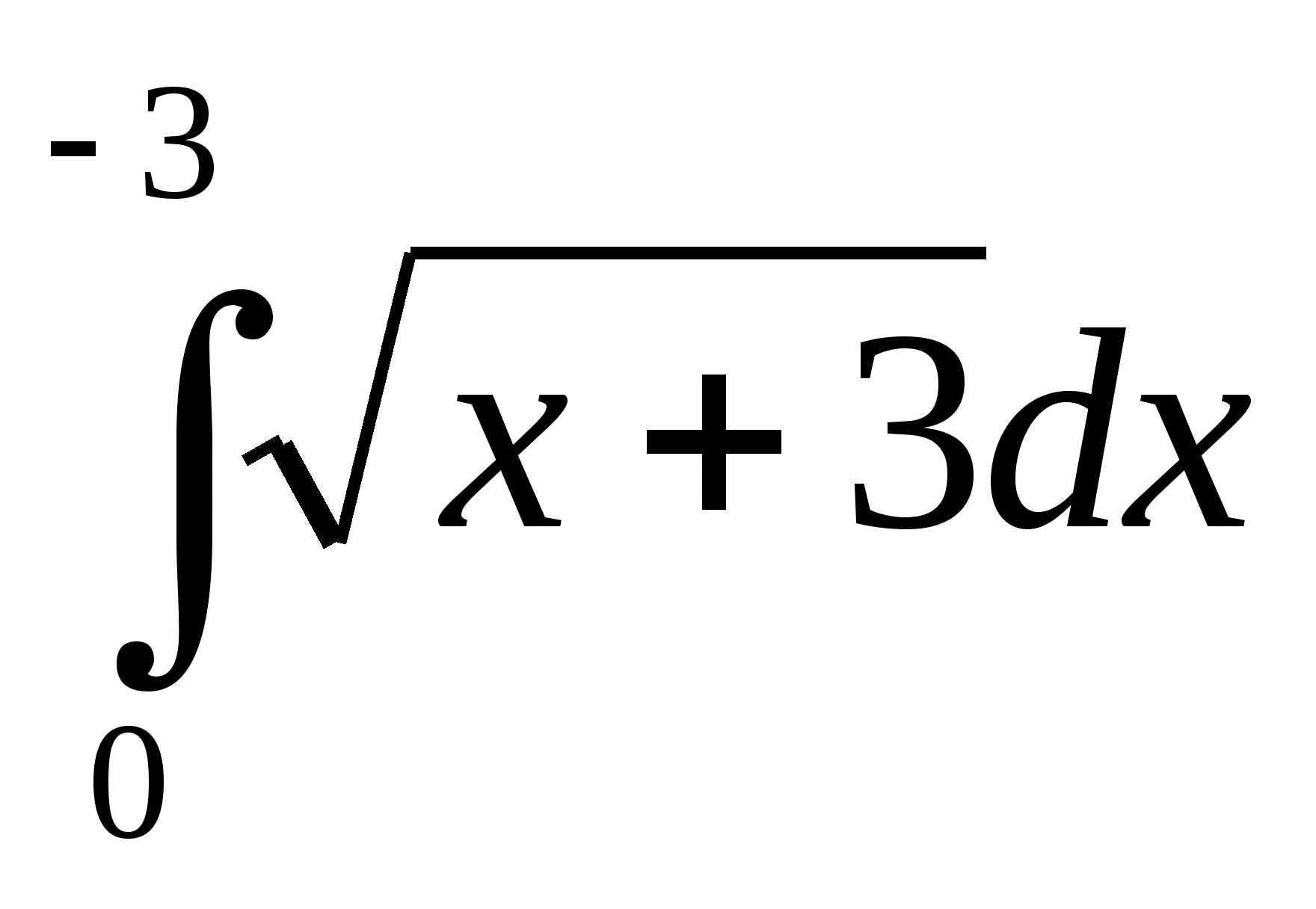

г) ;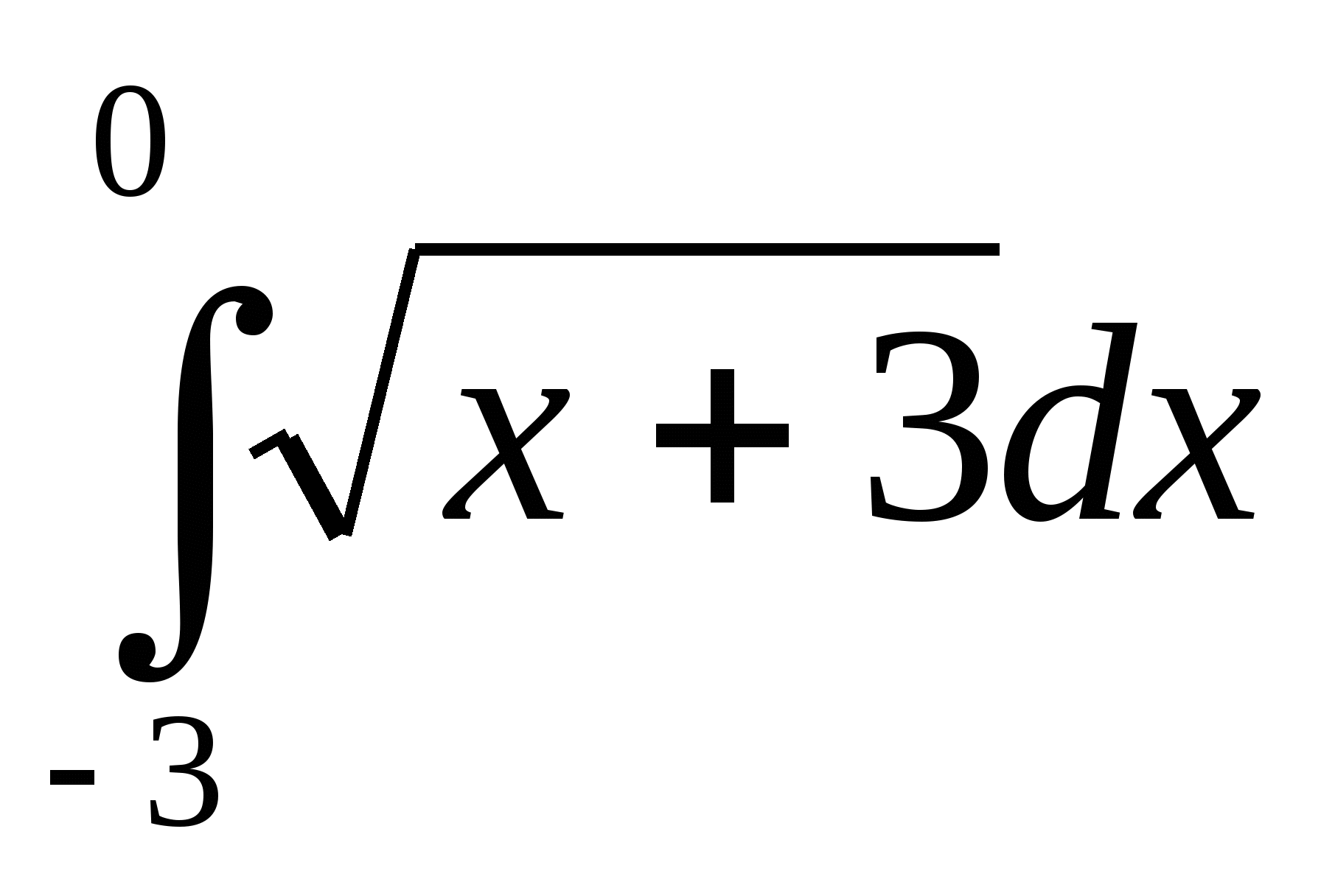

19. В результате подстановки t = 2 - 3х интеграл 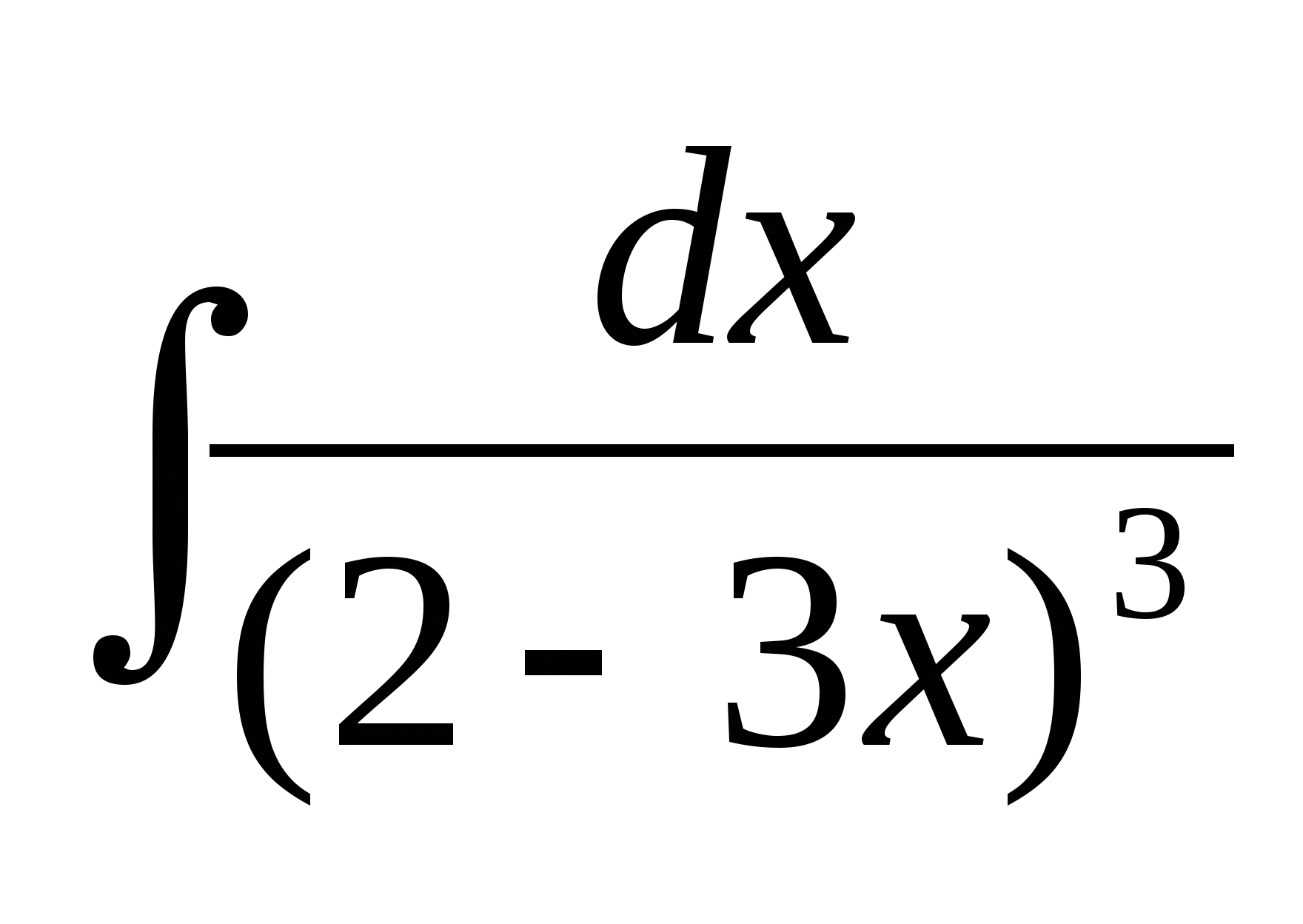приводится к виду:

а) ;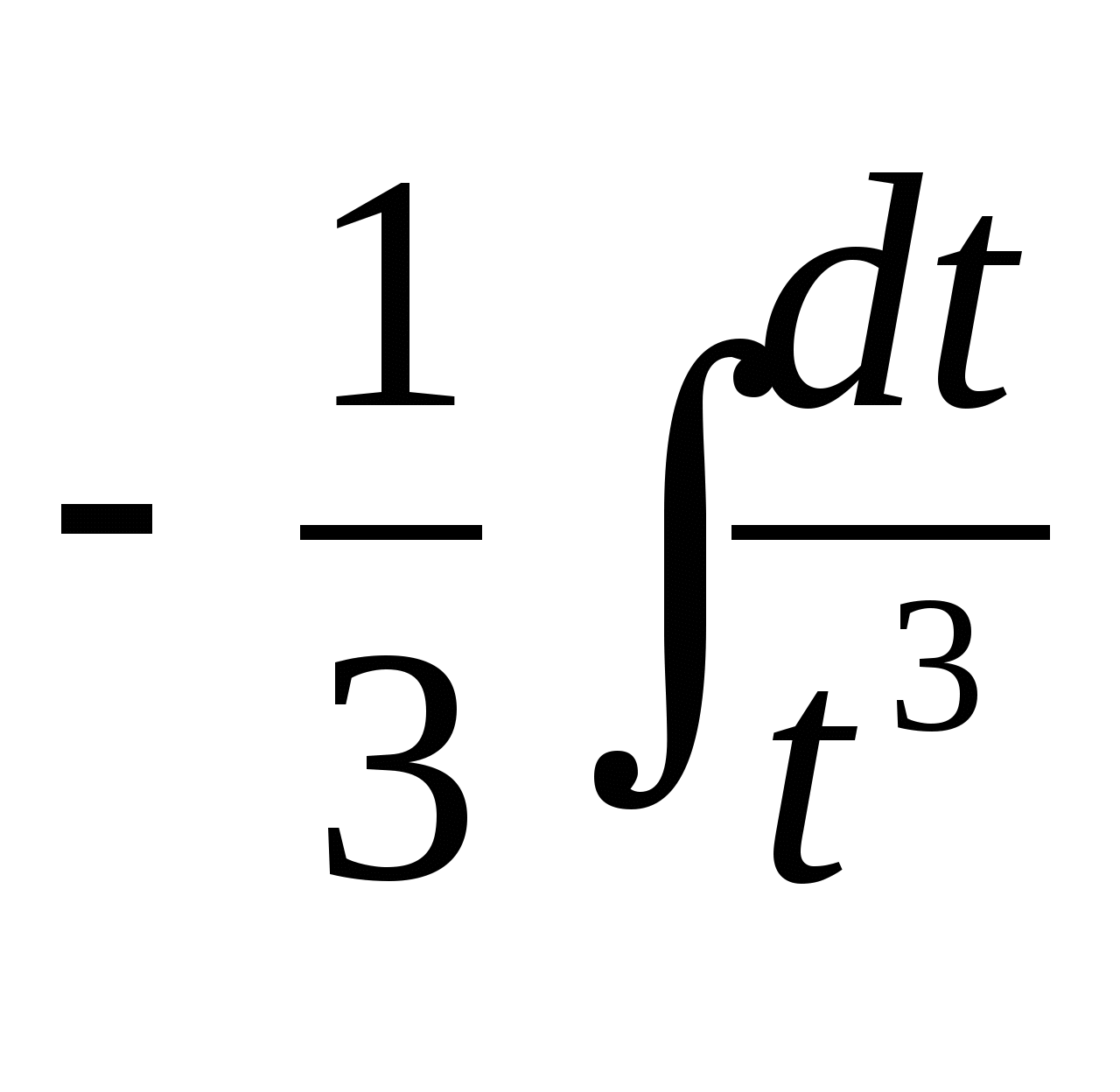

б) ;

в) ;

г) .

20. Множество всех первообразных функции у = имеет вид:

а) .

б) ;

в) ;

г) 3 ln х⁷ + С;

21. Интеграл 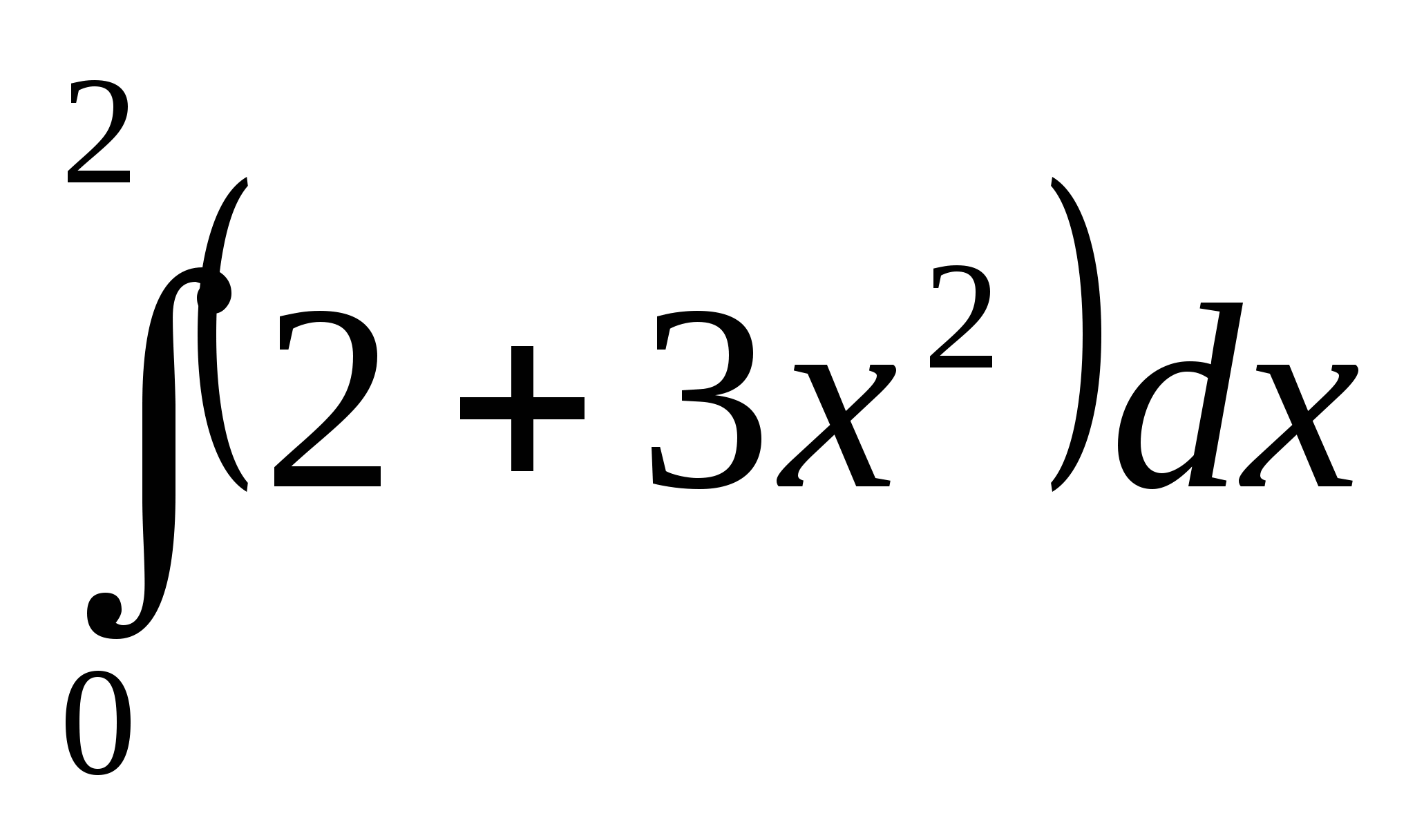равен…

Ответ внесите в поле

22. Скорость материальной точки, движущейся прямолинейно, равна υ (t) = 6-2t. Найдите, чему будет тогда равен путь, пройденный точкой от начала отсчета времени до остановки.

Ответ внесите в поле

Вариант №4

1. Производная функции у = х·Сos x имеет вид:

а) у' = cos x + x sin x;

б) у' = 1 - sin x;

в) у' = - sin x;

г) у' = cos x - x sin x.

2. Абсциссой точки перегиба графика функции у = 5 - +3 х² является:

а) 2;

б) -2;

в) 0;

г) 3.

3. Дана функция у = х³ - 2х² + 5. Установите соответствие между производными функции, в соответствующих точках, и их значениями:у' (2)

у' (-1)

у' (1)

а) 7;

б) -1;

в) 4.

4. Производная функции y = 6 arccos x, в точке х_о = 0 равна:

а) ;

б) -6;

в) 6;

г) 0.

5. Установите соответствие между функциями и их производными:;

;

.

а) f'(x) = ;

б) f'(x) = ;

в) f'(x) = .

6. Вторая производная функции f'(x) = 9х² - 14 равна:

Ответ внесите в поле

7. Расположите функции, определенные на всей числовой прямой, знаки производных которых указаны на рисунках по возрастанию количества точек максимума.а)

f '(х)

+

-

+

-

+

-

>

-1

0

2

4

6

х

б)

f '(х)

+

-

-

-

-

-

>

-1

0

2

4

6

х

в)

f '(х)

-

+

-

+

-

-

>

-1

0

2

4

6

х

г)

f '(х)

+

+

+

+

+

+

>

-1

0

2

4

6

х

8. Угловой коэффициент касательной к графику функции у = 3 - 2х - х² в точке х_о = 1 равен:

а) - 1;

б) 4;

в) 0;

г) - 4.

9. Предел равен…

Ответ внесите в поле

10. Определите значение предела :

а) ;

б) ;

в) ;

г) 0.

11. Определите два предела, значение которых равны 10.

а) ;

б) ;

в) ;

г) .

12. Определите, какие два из приведенных ниже предела, имеют значение равное 8.

а) ;

б) ;

в) ;

г) .

13. Вычислите приближенное значение степени (1,02)⁵.

а) 1,1;

б) 1,045;

в) 1;

г) 2.

14. Функция имеет разрыв в двух точках:

а) - 4;

б) 0;

в) -1;

г) 1.

15. Частными решениями дифференциального уравнения у'' - 3у' - 4у = 0 являются (выберите два и более варианта ответа):

а) у = sin х;

б) у = 2е^-х;

в) у = х² - 3х - 4

г) у = е^4х

16. Область определения функции имеет вид:

а) ;

б) ;

в) ;

г) .

17. К какому виду приводится интеграл 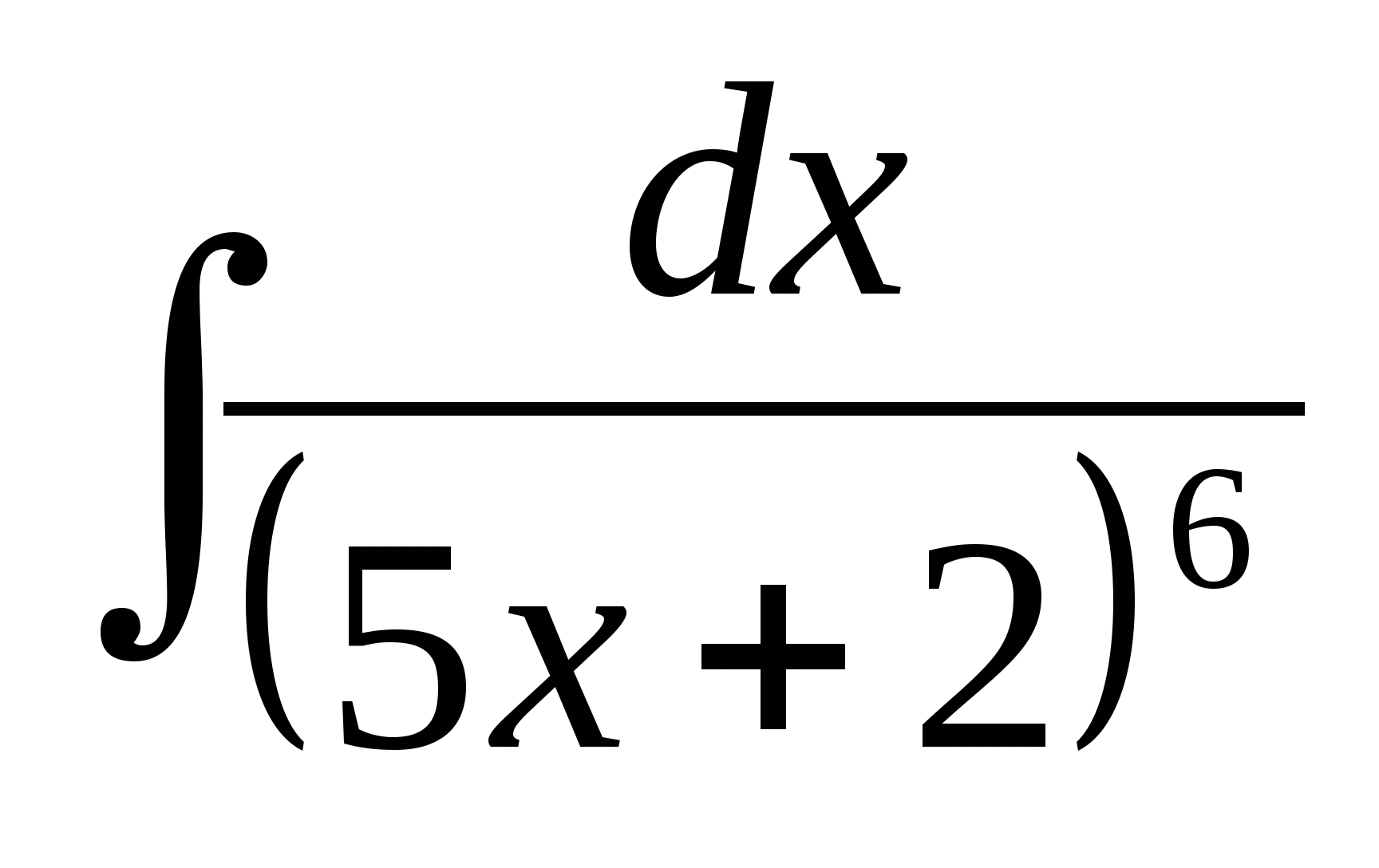в результате подстановки t = 5х + 2?

а) ;

б) ;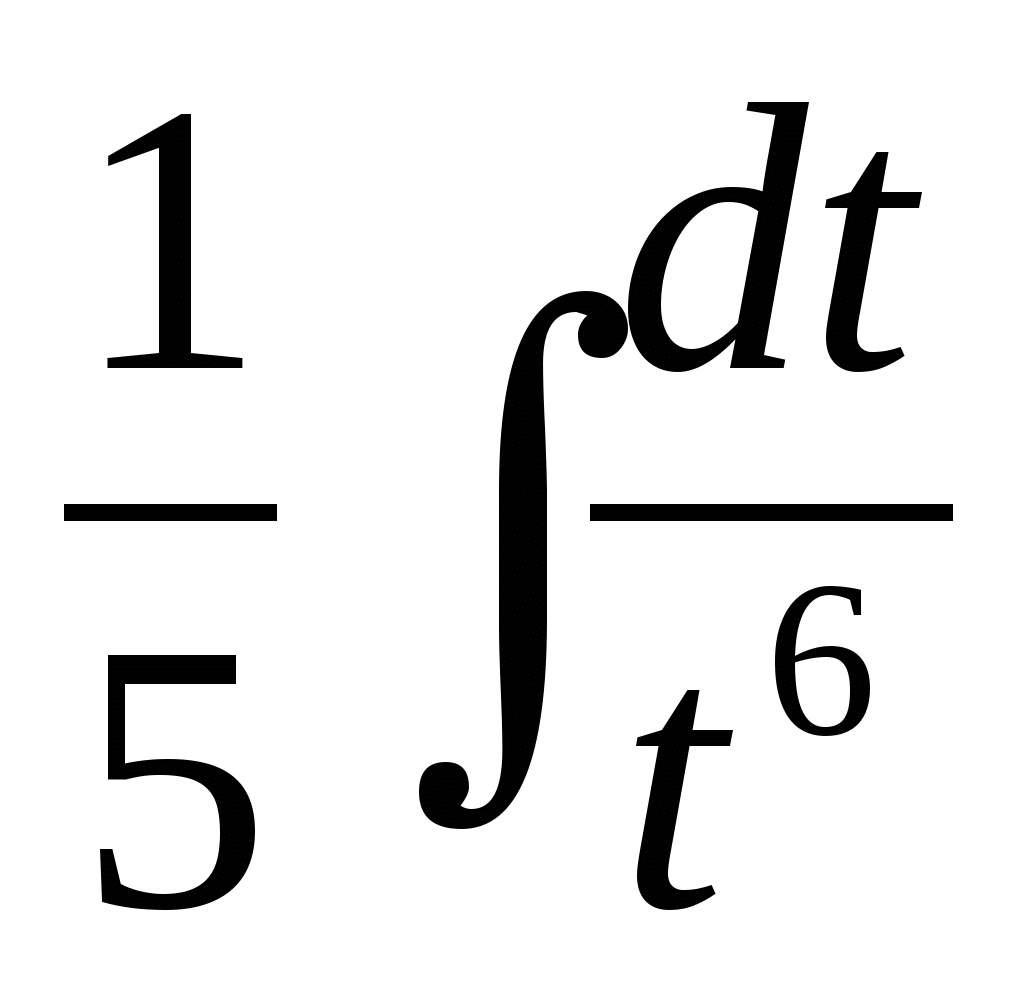

в) ;

г) .

18. Чему будет равен путь, пройденный точкой от начала отсчета времени до остановки, если скорость материальной точки, движущейся прямолинейно, равна υ (t) = 2 - t?

Ответ внесите в поле

19. Какой вид имеет множество всех первообразных функций у = 3х²?

а) х³;

б) 3х³ + С;

в) х³ + С;

г) 6х.

20. Площадь криволинейной трапеции Д определяется интегралом:

а) ;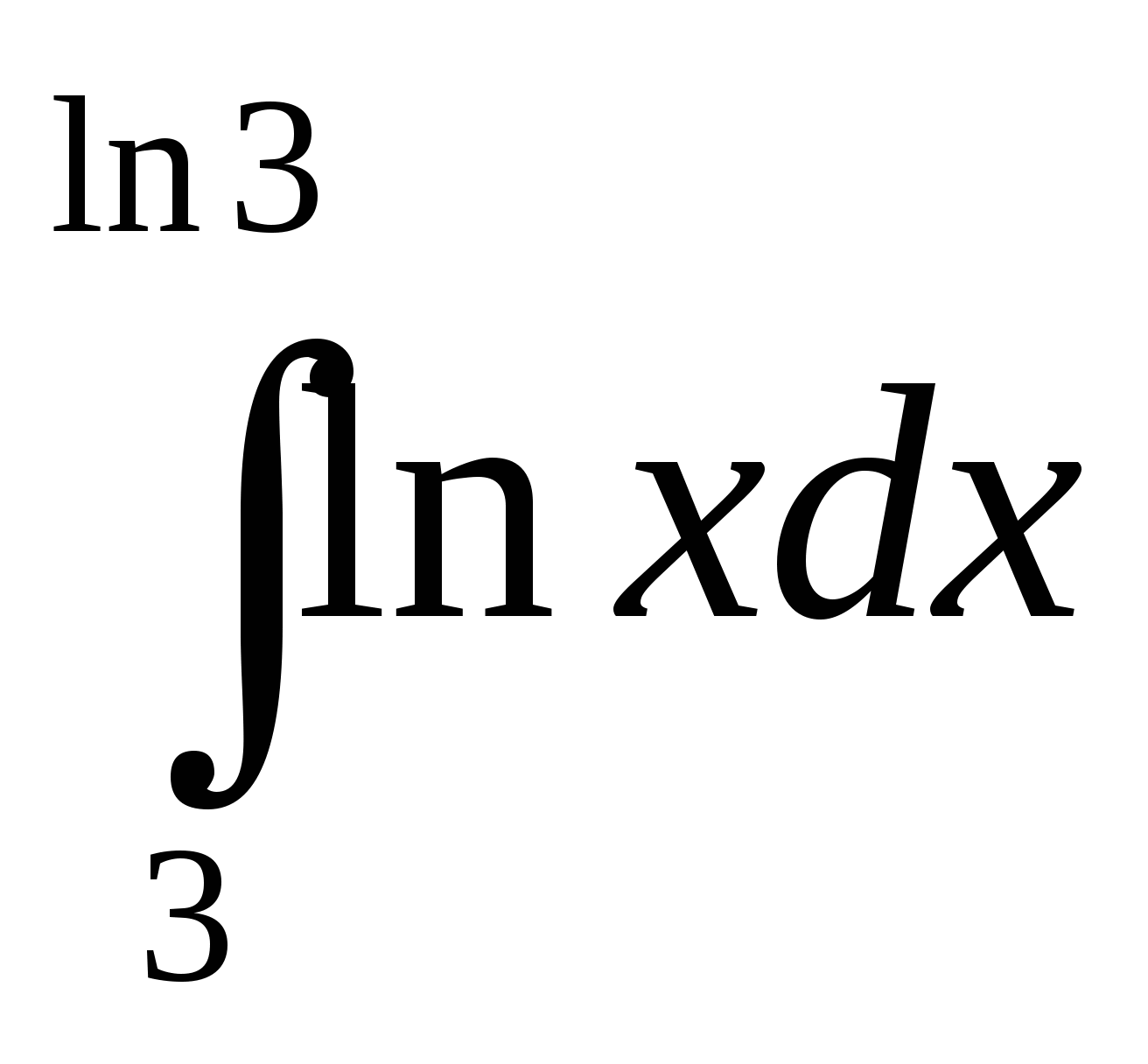

б) ;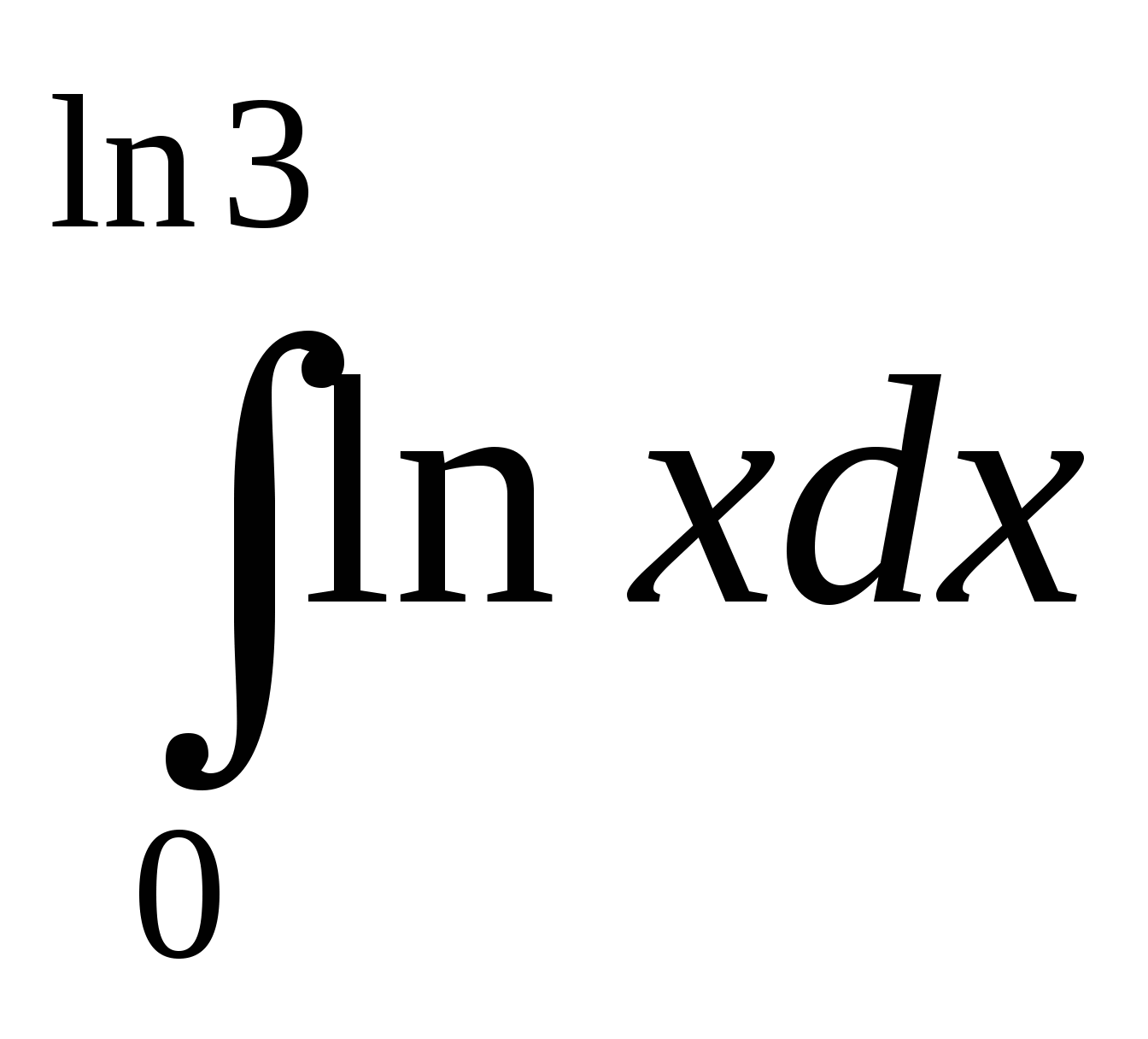

в) ;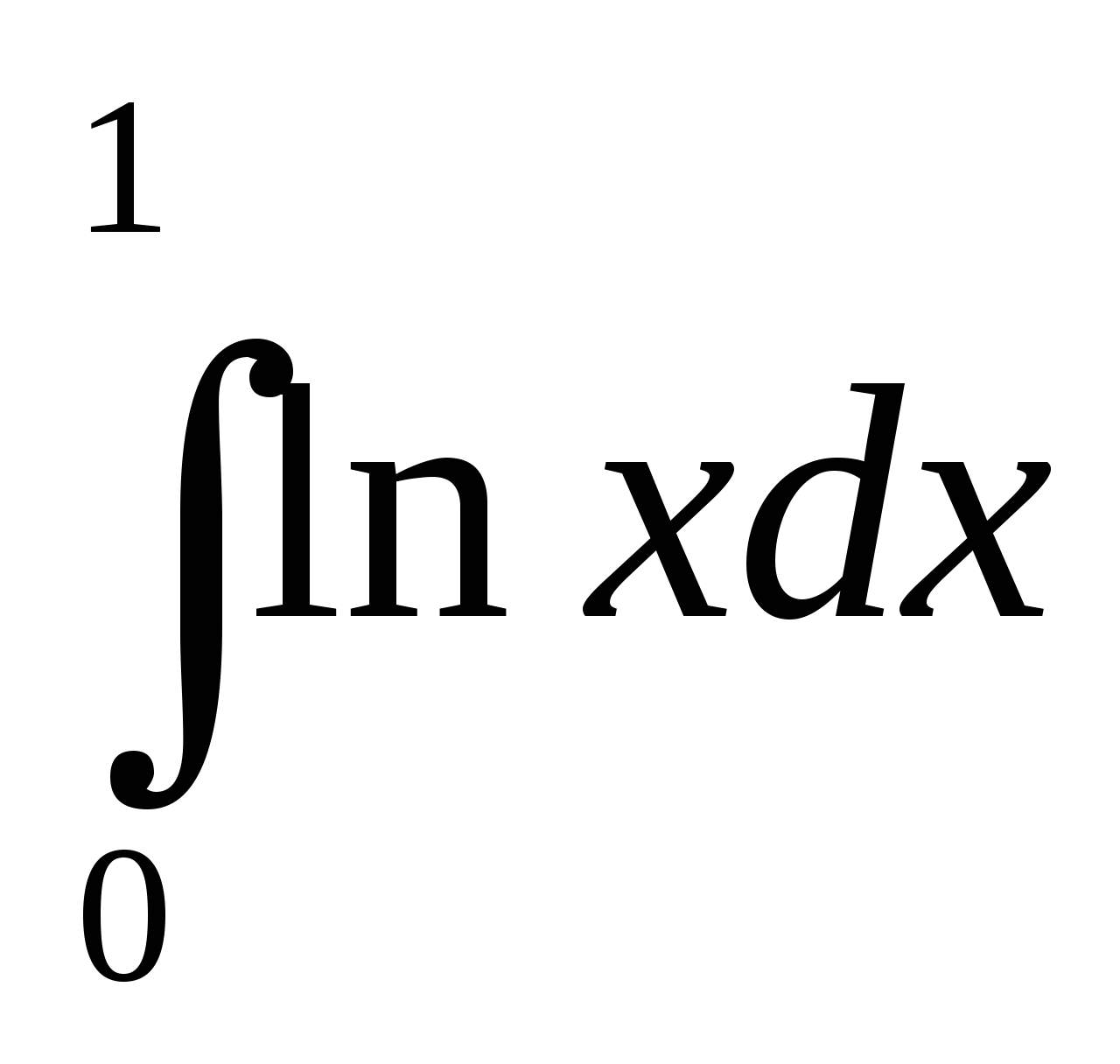

г) .

21. Используя свойства определенного интеграла, интеграл 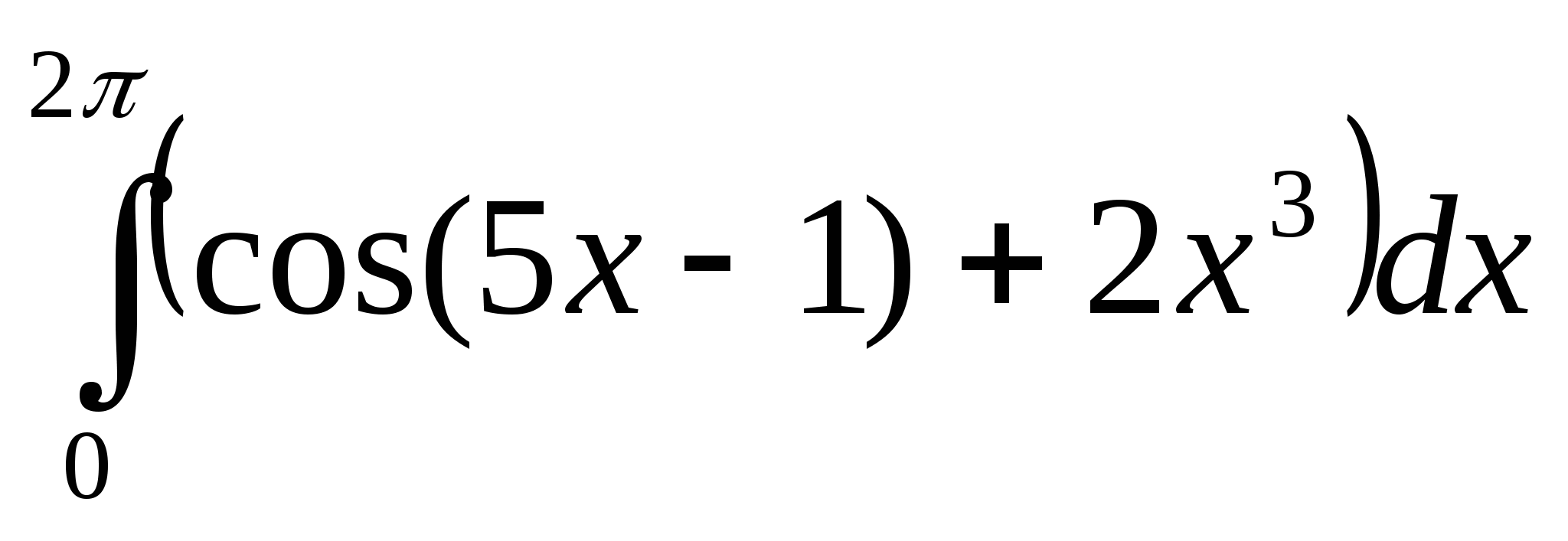можно привести к виду:

а) ;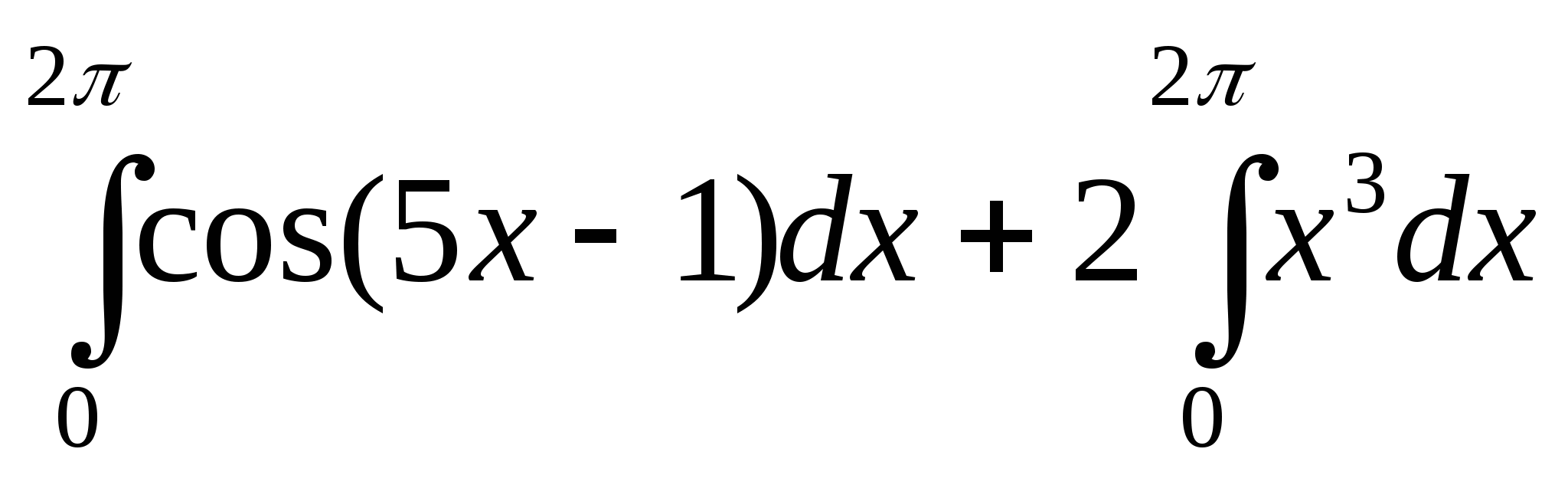

б) ;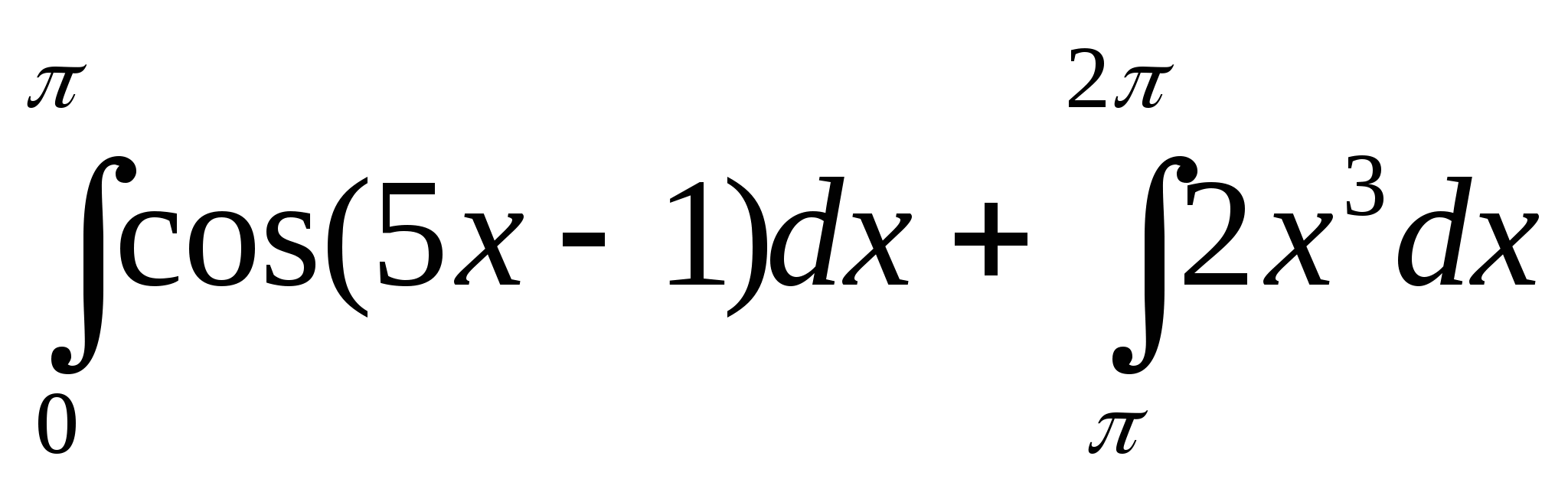

в) ;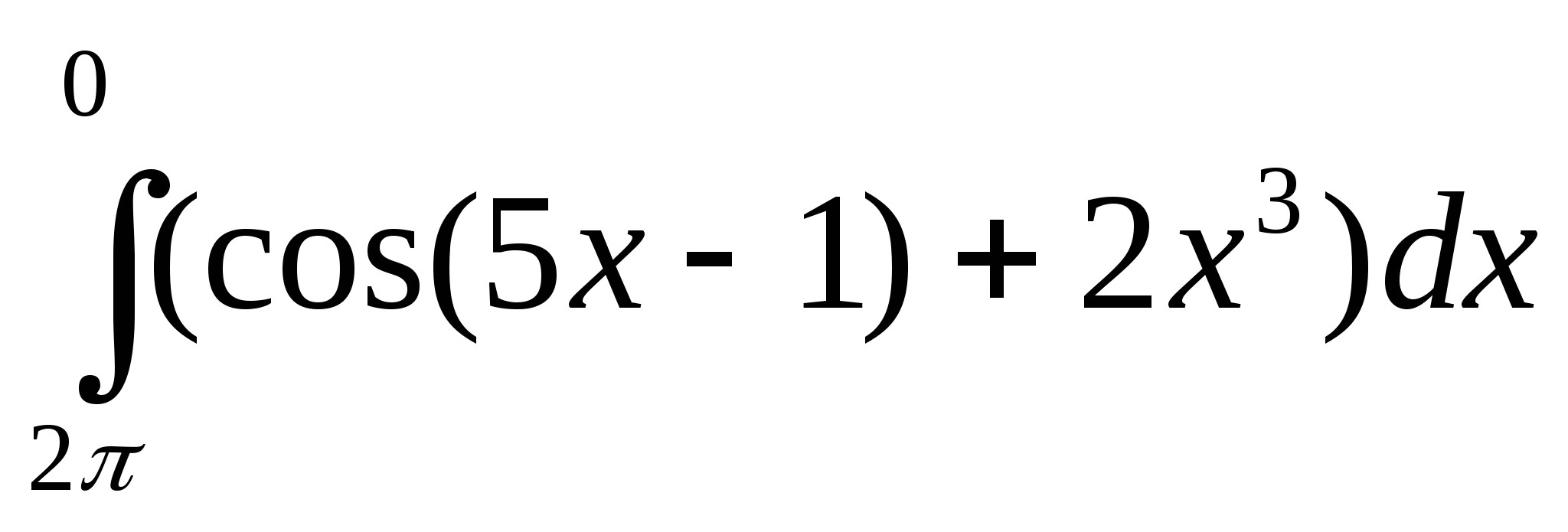

г) .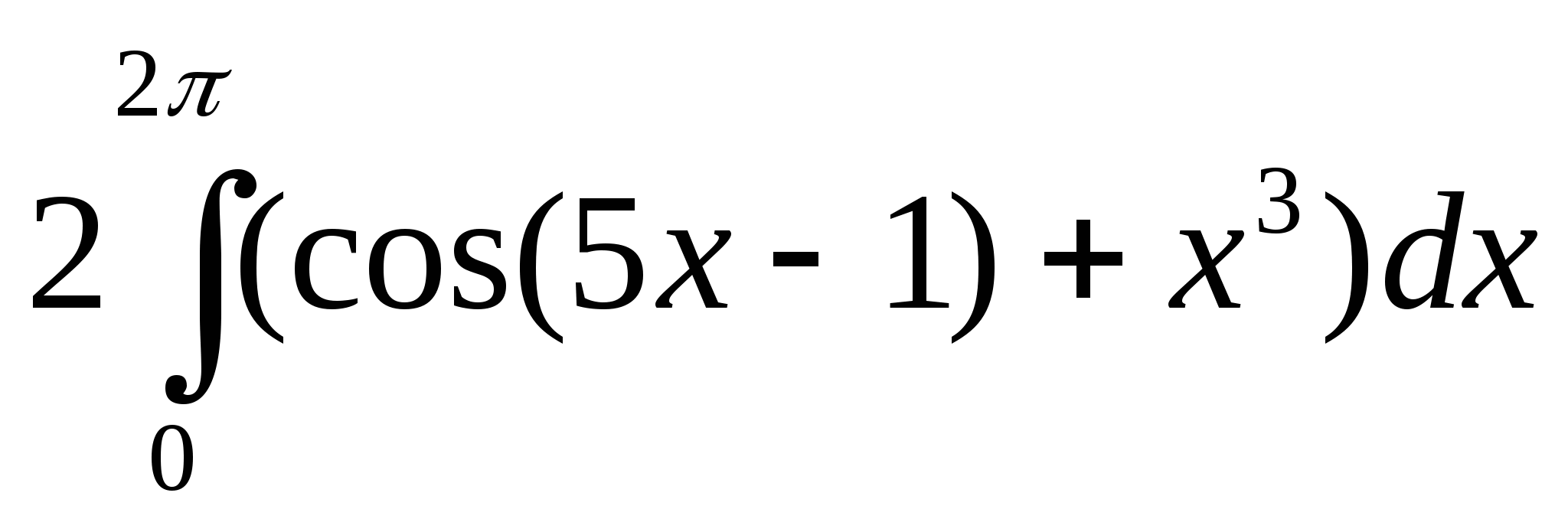

22. Определите, чему равен интеграл 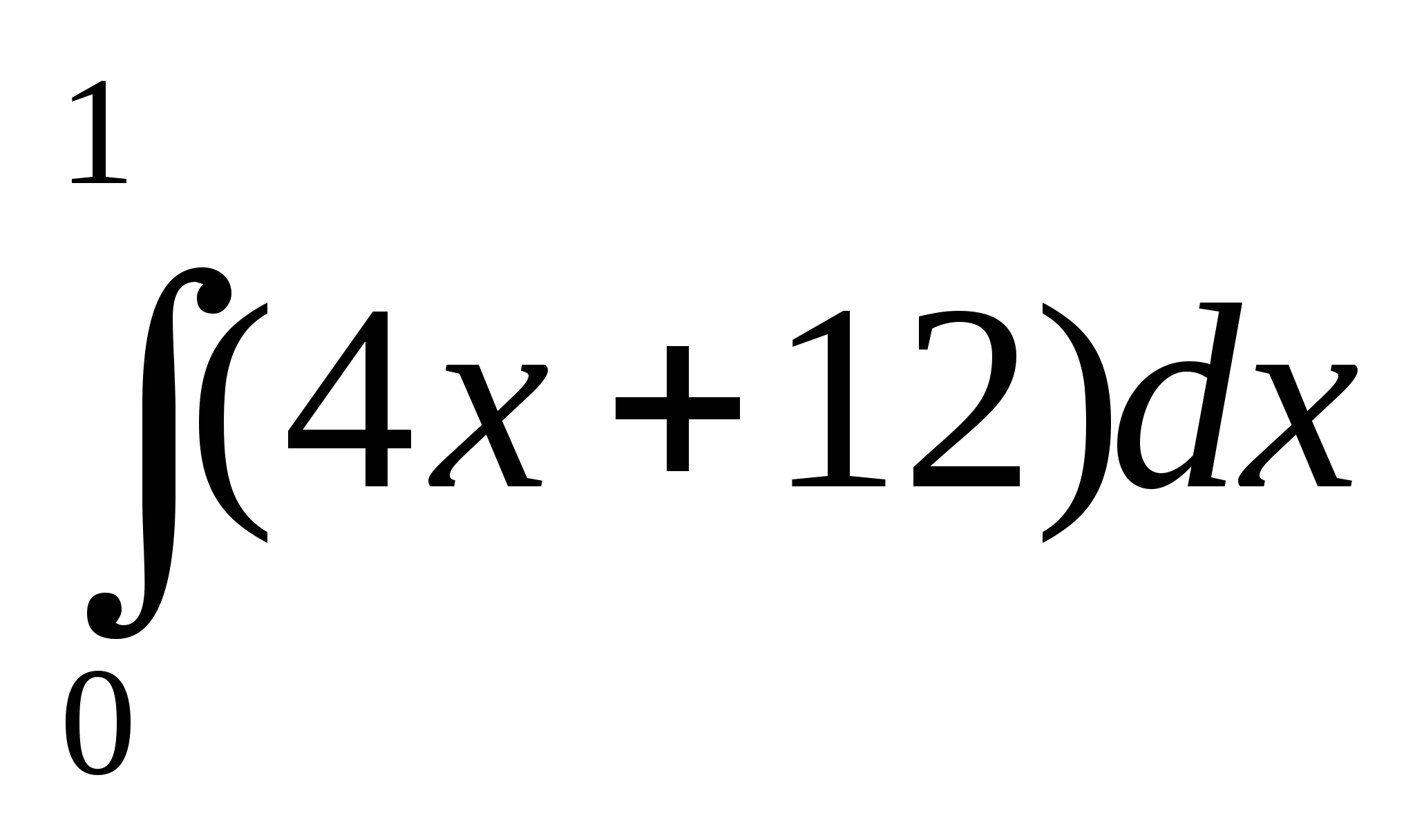?