- Учителю
- Логарифмическая функция, её свойства и график (11 класс)
Логарифмическая функция, её свойства и график (11 класс)
Тема: Логарифмическая функция, её свойства и график
Класс: 11
Цели урока: Образовательные - познакомить учащихся с логарифмической функцией, её свойствами, графиком; показать использование свойств логарифмической функции при решении заданий.
-
Развивающие - развивать мыслительные операции посредством сравнений, сопоставлений, обобщений, сознательного восприятия учебного материала, развивать зрительную память, развивать математическую речь учащихся, способствовать развитию творческой деятельности учащихся.
-
Воспитательные - воспитывать познавательную активность, чувства ответственности, уважения друг к другу, взаимопонимания, взаимоподдержки, уверенности в себе; воспитывать культуру общения.
Тип урока: урок изучения и первичного закрепления знаний и способов действий.
Методы обучения: индивидуальная работа, фронтальная работа, самостоятельная работа.
Средства обучения:
-
Мультимедийный проектор, экран, презентация.
-
Карточки для индивидуальной работы.
Форма обучения: групповая, индивидуальная, работа в статистических группах.
Ход урока
Этап урока
Задачи урока
Содержание урока
Формы работы
Методы
УУД
Контроль
Время
Деятельность учителя
Деятельность учащихся
Организационный момент
Подготовка учащихся к работе
- Здравствуйте ребята, присаживайтесь.
- На сегодняшнем уроке вы будете работать в группах. Результат работы группы будет зависеть от каждого из вас.
Учащиеся рассаживаются, слушают учителя.
1 мин
Актуализация опорных знаний и способов действий
Актуализация опорных знаний и умений
- Итак, начнем. Откройте тетради, запишите число, классная работа.
1.Сформулируйте определение функции.
2. Назовите функции, заданные формулами и соответствующие им графики.
![]()
![]()
![]()
![]()
(задание записано на слайде 2).
3. Вычислите, если это возможно:
Партнёры А
![]()
Партнёры В
![]()
Сималтиниус релли робин
Записывают в тетради число, классная работа.
Ученик отвечает Функция - это зависимость между двумя множествами, при котором каждому элементу из одного множества ставится в соответствии с некоторым правилом, законом единственный элемент из другого множества
Ученики по просьбе учителя рассказывают, что является графиком соответствующей функции.
Самостоятельно выполняют
меняются карточками с результатом своей работы с партнёром по плечу: сравнивают, вырабатывают общий вариант
Учащиеся предлагают варианты целей урока.
Фронтальная
Наглядно-практические
Беседа
Анализ Синтез
Познавательные: анализ объектов с целью выделения признаков; синтез как составление целого из частей, в том числе самостоятельно достраивая, восполняя недостающие компоненты; выбор оснований и критериев для сравнения, классификации объектов.
Устный
5 мин
Изучение нового материала
Развивать творческое мышление учащихся
Формировать умения высказывать свое мнение, делать выводы
Обозначьте изменяющуюся величину через x. При этом значение логарифма тоже будет изменяться. Обозначьте его через y и задайте формулой полученную зависимость y от x.
Итак, ребята, что у вас получилось?
Задаются ли этими формулами функции? Объясните, почему?
Посмотрите внимательно на правую часть формулы.
Подумайте, как бы вы назвали эту функцию?
Объявляется тема урока с записью в тетрадях.
Учащиеся работают.
Запись на доске: ![]() и
и ![]()
Учащиеся предлагают варианты
Слушают учителя. Записывают в тетради тему урока
Устный
2 мин
Обеспечение мотивации и принятия учащимися цели учебной деятельности
Постановка целей урока
Формировать умения высказывать свое мнение, делать выводы
А находит ли применение эта функция в окружающем нас мире?! А может это просто прихоть математиков?! Наверно нет! Ведь всякое явление можно описать с помощью функции. Давайте убедимся, что и логарифмическая функция находит своё применение.
Об этом нам расскажет ваш одноклассник. Я попросила Фатыхова Ленара подготовить сообщение о том, где встречается логарифмическая функция.
Давайте подумаем, какие цели мы ставим перед собой на сегодняшний урок.
Учитель обобщает и корректирует сформулированные учениками цели, после чего они появляются на слайде
Выступление ученика по детской презентации "Логарифмы в окружающем мире"
Коммуникативные: самостоятельное выделение и формулирование познавательной цели.
Регулятивные: осуществлять целеполагание.
Устный
2 мин
Умение быстро вычислять значения логарифмов
МИКС -ФРИЗ-ГРУП Проведем небольшую разминку, вспомним свойства логарифмов ![]()
![]()
![]() lg 100 = 2
lg 100 = 2 ![]()
![]()
Ученики смешиваются под музыку, замирают, когда музыка прекращается и объединяются в группы, в зависимости ответа на вопрос.
1 мин
Развивать творческое мышление учащихся
Формировать умения высказывать свое мнение, делать выводы
Нами получено только два примера логарифмической функции. Их существует множество. Как получить это множество? Какие значения могут принимать эти числа?
Так какую же функцию мы назовём логарифмической?
Даётся определение логарифмической функции.
О чём мы обычно ведём разговор, когда рассматриваем какую-либо функцию?
Возможно, ученики ответят: вместо "2" или "1/2" подставить другие числа.
Больше нуля, не равны 1
Ученики отвечают
Функцию, заданную формулой y = logax (где а > 0 и а ≠ 1), называют логарифмической функцией с основанием а.
Возможно ученики ответят:
-
свойства
-
график.
Личностные: умение вести диалог на основе равноправных отношений и взаимного уважения.
ЭЙ АР ГАЙД - сравнивание точки зрения до выполнения упражнения
1.Ось Оу является вертикальной асимптотой графика логарифмической функции.
2. Графики показательной и логарифмической функций симметричны относительно прямой у = х.
3.Область определения логарифмической функции - вся числовая прямая, а область значений этой функции - промежуток (0; + ∞).
4.Монотонность логарифмической функции зависит от основания логарифма.
5.Не каждый график логарифмической функции проходит через точку с координатами (1; 0).
6.Логарифмическая функция является ни чётной, ни нечётной.
7. Логарифмическая функция непрерывна
Ответить на вопросы: да или нет
Каждый ученик отвечает на листочке.
Познавательные: анализ объектов с целью выделения признаков
1 мин
Исследовать свойства логарифмической функции
Для исследования свойств функции учащимся в группах необходимо построить график предложенных функций.
Учащиеся выполняют предложенные задания и делают вывод о свойствах функции
Свойства записываются в тетрадь.
Групповая
Анализ Синтез
Исследовательский
Беседа
Объяснительно-иилюстративный
синтез как составление целого из частей, в том числе самостоятельно достраивая, восполняя недостающие компоненты.
Устный
8 мин
1) y = log2x
x
1/4
1/2
1
2
4
8
y = log2x
- 2
- 1
0
1
2
3
Свойства логарифмической функции при a > 1 (слайд 8)
-
Область определения - множество всех положительных чисел R+.
-
Область значений - множество всех действительных чисел R.
-
Функция является ни четной, ни нечетной
-
При всех значениях а график логарифмической функции пересекает ось абсцисс в точке х = 1.
-
Промежутки знакопостоянства:
y > 0 при x ![]() (1;+∞)
(1;+∞)
y < 0 при x ![]() (0;1)
(0;1)
-
Функция возрастает при x
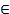 (0;+∞)
(0;+∞) -
Функция непрерывна
2) y = ![]()
x
1/4
1/2
1
2
4
8
y = ![]()
2
1
0
- 1
- 2
- 3
Свойства логарифмической функции при 0 <������������������������)
-
Область определения - множество всех положительных чисел R+.
-
Область значений - множество всех действительных чисел R.
-
Функция не является ни четной, ни нечетной
-
При всех значениях а график логарифмической функции пересекает ось абсцисс в точке х = 1.
-
Промежутки знакопостоянства:
y > 0 при x ![]() (0; 1)
(0; 1)
y < 0 при x ![]() (1; +∞)
(1; +∞)
-
Функция убывает при x
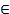 (0; +∞)
(0; +∞) -
Функция непрерывна.
Закрепление изученного материала
Для закрепления изученного материала предлагаю выполнить следующие задания 1. Устно: определите, какие из перечисленных ниже функций являются возрастающими, а какие убывающими? (слайд 12)
y = log3x;
y = log23x;
![]()
y = log0,5(2x + 5);
y = log3(x + 2).
2. Задание I-го уровня: решить графически уравнения: (слайд 13)
Решение:
а) lgx = 1 - x (слайд 14)
3. Задание II-го уровня: используя свойства логарифмической функции, сравнить: (слайд 15)
Отвечают устно
Один учащийся работает у доски, остальные на местах.
Ответ: х = 1.
Работа в группах с последующей самопроверкой
Фронтальная работа
Упражнения
Метод демонстраций
Упражнения
Познавательные: осуществлять расширенный поиск информации с использованием ресурсов Интернета
Устный
2 мин
4 мин
8 мин
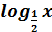
Решение:
а) Логарифмическая функция с основанием, большим 1, возрастает на всей числовой прямой. Так как
3 < 5, то log23 <��������������
������������![]() ����е 1, поэтому функция у =
����е 1, поэтому функция у = ![]() убывает, следовательно,
убывает, следовательно, ![]() .
.
в) Логарифмическая функция с основанием, большим 1, возрастает, следовательно, ![]() .
.
г) Логарифмическая функция с основанием, меньше 1, убывает, следовательно, ![]() <�������
<�������![]() ����
����
�����������
����������������������������������������������
���������������������������������������������������������������
����ки показательной и логарифмической функций симметричны относительно прямой у = х.
3.Область определения логарифмической функции - вся числовая прямая, а область значений этой функции - промежуток (0; + ∞).
4.Монотонность логарифмической функции зависит от основания логарифма.
5.Не каждый график логарифмической функции проходит через точку с координатами (1; 0).
6. Логарифмическая функция является ни чётной, ни нечётной.
7.Логарифмическая функция непрерывна.
Изменились ли ваши убеждения ? Почему? Какие утверждения самые важные для вас? Почему?
Финк-райт-раунд-робин учащиеся думают, записывают ответ и по очереди обсуждают свои ответы в команде
Фронтальная работа
Проблемный
Познавательные: анализ объектов с целью выделения признаков
5 мин
Постановка домашнего задания
Учитель сообщает домашнее задание Изучить п. 10 стр 90-95.Выполнить
I уровень: № 10.3 II уровень: № 10.6
Комментирует задания.
Записывают домашнее задание.
Фронтальная
Объяснение
1 мин
Подведение итогов урока
Сделать выводы по уроку
- Подводя итоги урока, оцените себя, ответив на следующие вопросы
Учащиеся отвечают на вопросы или заканчивают фразу.
Фронтальная
Личностные, регулятивныеспособность рефлексировать. Коммуни кативные: выстраивание логической речи.
3 мин
VIII этап урока. Рефлексия
Выразите ваше отношение к уроку (выбрать смайлик)
1. Вы считаете, что урок прошел плодотворно, с пользой. Вы научились и можете помочь другим.
Я доволен собой!

2. Вы считаете, что научились, но вам еще нужна помощь.
Я вполне доволен собой!

3. Вы считаете, что было трудно на уроке.
не нужна помощь!

- Спасибо за урок!