Конспект урока (и самоанализ урока) по математике «Правильные и неправильные дроби» (5 класс)

Муниципальное образовательное учреждение

Уренская средняя общеобразовательная школа №1

Конспект урока

Тема: «Правильные и неправильные дроби».

Выполнила:

Слепышева Наталья

Александровна

учитель математики

МОУ УСОШ №1

г. Урень

2010 год

Урок «Правильные и неправильные дроби» (5 класс)

Методические комментарии. На изучение темы «Правильные и неправильные дроби» в 5 классе отводится 1 час. Понятия правильной и неправильной дроби включают в себя определения и свойства (возможно также изучение признаков) и представляют собой компактную модель математиче­ского понятия. Небольшой объем и невысокая сложность материала позво­ляют уложить в отведенные рамки не только традиционное содержание те­мы, но и довольно обширный методологический компонент содержания. Это создает предпосылки для знакомства на доступном для пятиклассников уровне с процессом возникновения и развития понятия в математике.

Усвоение методологических знаний на предлагаемом уроке идет по нескольким направлениям:

• знакомство с различными видами математических предложений (определение, гипотеза) и их ролью в решении задач и изучении тео­рии;

• осознание содержания понятия как совокупности взаимосвязанных
  фактов, отраженных в определении, свойствах и признаках;

• знакомство с методом познания - классификация.

Конспект урока

Ход урока.

Мотивационно-ориентировочная часть.

Организационный момент.

1. Актуализация имеющихся знаний и умений учащихся.

• Итак, ребята, давайте с вами вспомним, какую тему мы изучали на послед­них нескольких уроках математики?

• - Чему вы научились за время изуче­ния этой темы, покажут задачи, кото­рые я предлагаю вам решить:

• Дроби.

(выполняют задания устно и у дос­ки)

1. Прочитайте дроби: ; ; ; ; . Назовите числитель, знаменатель каждой дроби. Что показывает числитель и знаменатель дроби?

2. Запишите дробью: арбуз разрезали на 16 равных частей, за обедом съели 7
таких долек. Какую часть арбуза съели за обедом? Какая часть арбуза осталась?

3. Как иначе можно записать дроби ; ; ? Как записать 1 в виде дроби с числителем 3? со знаменателем 4? с произвольным знаменателем?

4. Сравните дроби: и ; и ; и ; и .Какие дроби мы умеем сравнивать? Как сравнить дроби с одинаковыми знаменателями?

2. Создание проблемной ситуации, мотивация.

(сравнение последней пары вызывает у учащихся затруднения)

• Почему вы не можете сравнить две - последние дроби?

• Хотели бы вы научиться сравнивать такие дроби?

• Мы учились сравнивать только дроби с одинаковыми знаменателя­ми, а у этих дробей знаменатели разные.
  - Конечно,
  
  

3. Постановка учебной задачи (цели) урока.

-Как вы думаете, чем мы будем сегодня заниматься на уроке?

- Будем учиться сравнивать дроби с разными знаменателями.

- А я предлагаю выбраться из затруднительного положения так, как предпочитают это делать ученые - математики - решить более общую за­дачу: изучить числа, похожие на предложенные дроби, выяснить их свойства, дать им названия, а затем использовать их для решения задачи. Принимаете предложение?

Как же сформулировать нам цель работы на уроке? (фиксирует предложенные варианты на доске)

- Изучить дроби, похожие на дроби из последней пары.

- Изучить дроби с разными знаменателями

- Вижу, что сейчас нам сложно сформулировать цель урока, давайте тему урока и его цель запишем позже, когда сможем более четко охарактеризовать эти дроби.

. телями.

II. Операционно-познавательная часть,

1. Выделение существенных свойств понятия.

На доске записаны дроби:

Сравните числитель, и знаменатель каждой дроби.

Добавьте к ним дроби и и разбейте все дроби на группы так, чтобы эти дроби оказались в разных группах. Можете работать самостоятельно в парах.

(работают индивидуально или в прах 2-3 минуты)

- Как вы разделили дроби на группы?

I группа: ; ;; ;;; .

II группа: ; ; .

III группа: ; ;; ;.

• В подобных ситуациях ученые говорят, что произведено разбиение на классы. Его проводят для того, чтобы изучить не каждый объект в отдельно­сти, а целый класс похожих между собой объектов. Такой способ исследования называют методом классифика­ции. Он часто используется в науке(например, классификация растений и животных, в биологии). Очень важным является выбор свойства, по которому
  производится разбиение на классы -
  основания классификации. Это свойство должно быть существенным, от­ражающим характерные особенности исследуемых объектов.­

Поясните, по какому принципу мы произвели разбиение на классы.

Каково было основание классификации?

- В первую группу собраны дроби, которые имеют числитель меньше знаменателя, у дробей второй груп­пы числитель равен знаменателю, в третьей группе - дроби, числитель которых больше знаменателя.

-Те свойства, что мы указали, являются важными, существенными для проведенного разбиения. Их также называют характеристическими свойствами для каждой группы, а каждая группа имеет собственное название: дроби первой группы называют правильными, второй и третьей групп - непра­вильными.

Думаю, что теперь мы можем записать тему урока и уточнить его цель. Принимаю ваши предложения.

(делают соответствующие записи на доске и в тетрадях).

- Тема «Правильные и неправиль­ные дроби». Цель урока - изучить правильные и неправильные дроби.

Как именно мы хотели бы их изучить? - установить свойства правильных и неправильных дробей. Запишите тему и цель урока в тетрадях. Сделаем это в необычной форме, в виде следующей схемы. На что она похожа?

­

На рыбный скелет.

В голове рыбы мы с вами запишем тему нашего урока, в одной части скелета будем отмечать новые для нас понятия и свойства, а в другой части скелета будем указывать, где они используются и применяются, в хвосте рыбы запишем вывод и подведём итог нашего урока.(Работа со схемой, заносится тема и цель урока)Приложение №1.

2. Моделирование определения.

- Вернемся к трем группам дробей.

Вспомните, по какому признаку мы

произвели разбиение и опишите

какую дробь называют правильной дробью? Неправильной дробью?

- Правильной дробью называют та- кую дробь, числитель которой, меньше знаменателя;

-Дробь называется неправильной, знаменателю если ее числитель больше или равен

На доске выписываются в два столбца род и видовые отличия каждого понятия:

Правильной дробью называют:

1)дробь

2)числитель, которой меньше знаменателя.

Неправильной дробью называют:

1) дробь

2)числитель которой больше ее знаменателя или

3)равен знаменателю.

- Сравните выписанные предложения.
Что в них общего, и чем они отличаются?

- Предложения похожи по своему строению, в обоих присутствует слово «называют».

• Оба предложения повествуют о
  видах дробей, указывают их общие
  и отличительные (характеристические) свойства.

• Количество свойств может быть
  различным и сами свойства различаются.

-Такого вида предложения в матема­тике называют определениями.

-Что нового мы узнали на данном этапе урока?

На дос­ке выписаны определения правильной и неправильной дроби. Встречались ли мы раньше с определениями в математике? Сформулируйте их.

-Как вы думаете, зачем нужны определения, каково их назначение в математике?

определения правильной и неправильной дроби( это заносится в схему рыбы)

(формулируют определения уравнения, корня уравнения, отрезка, луча и т.п.)

- Они дают названия, имена понятиям, заменяют длинное описание более коротким.

- Определения описывают, раскрывают, что понимается под каким-то словом (термином).

- С их помощью люди «договариваются» о точных названиях для понятий.

3.Осознание определения и способов его получения.

Мы сказали, что у определений в ма­тематике двойная роль - называть новые понятия и раскрывать термин. Но тем самым определения помогают нам
в решении задач. Убедитесь в этом при выполнении заданий, записанных на доске.

1. Назовите среди дробей 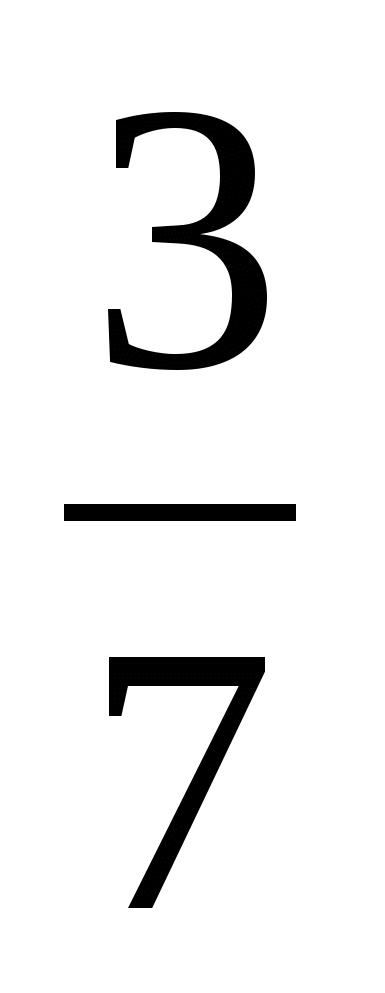; ; 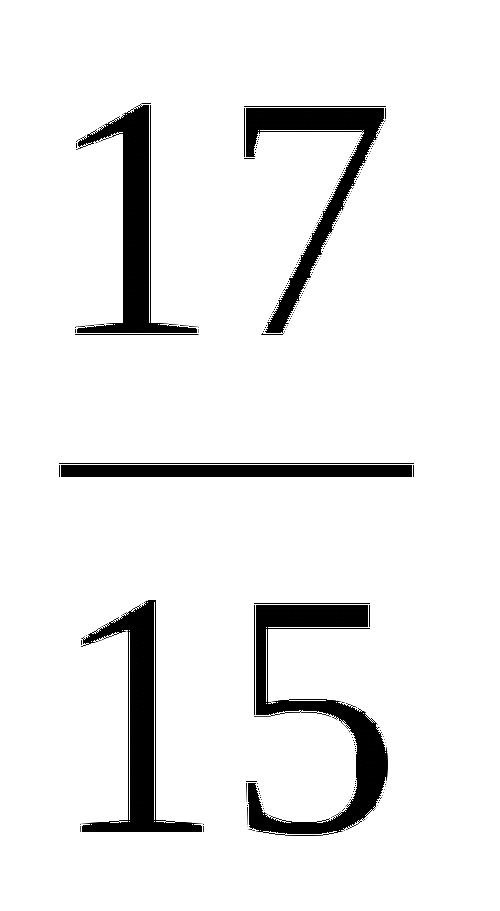; ; 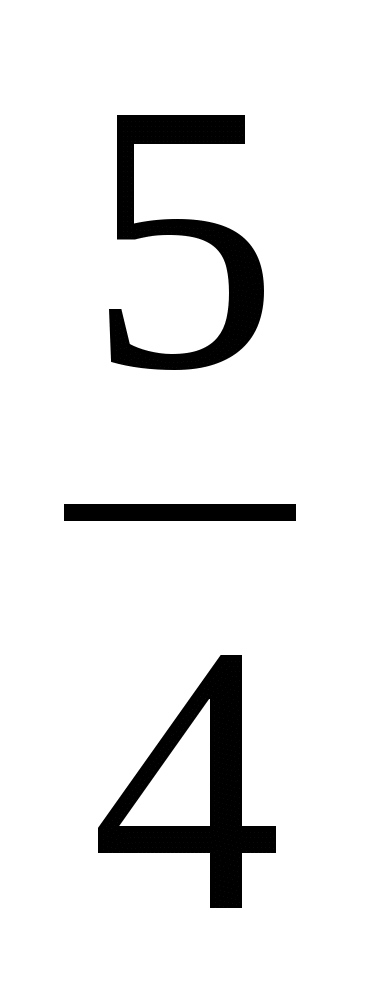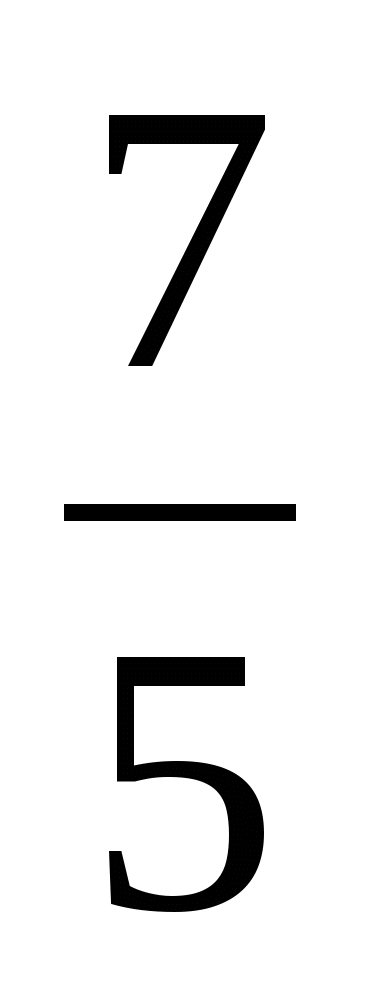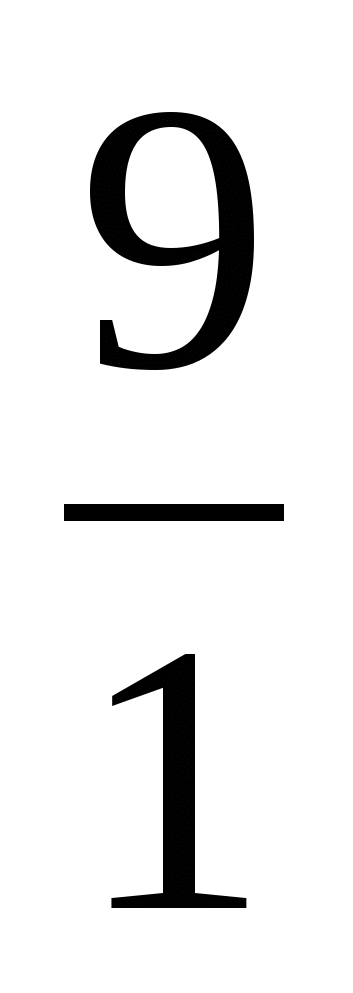правильные (неправильные), обос­нуйте (докажите) свой ответ.

2. Приведите пример правильной (неправильной) дроби, обоснуйте свой от­вет.

3. Запишите все возможные правильные (неправильные) дроби со знаменателем 7; с числителем 5. Корректно ли это задание? Почему?

4. Известно, что х > у. Является ли дробь 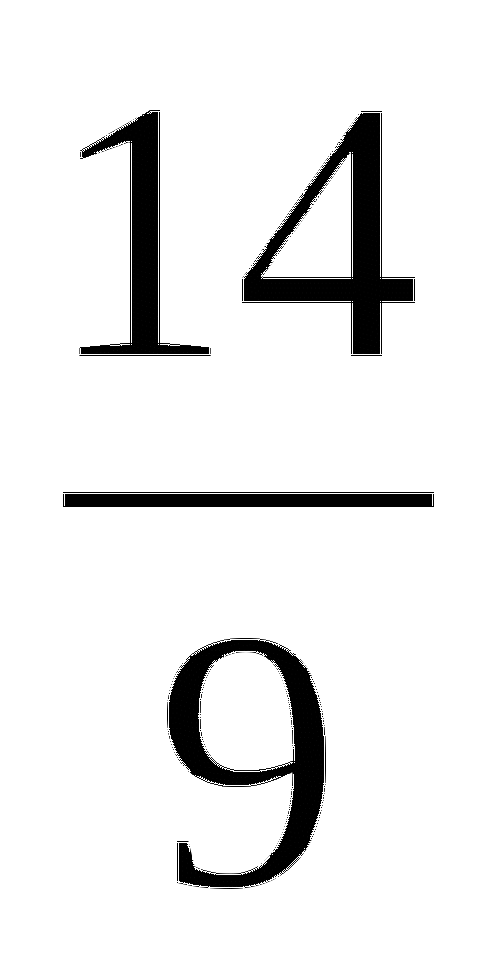- правильной? Обоснуйте свое утверждение.

5. При каких значениях «с» дробь 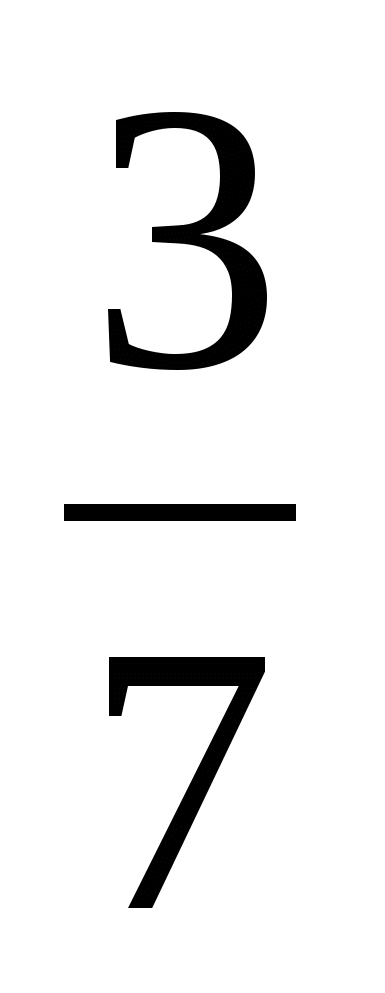будет неправильной?

6. При каких значениях t дробь будет правильной?

- Какие задания вам показались похожими? Что в них общего?

- Есть ли еще похожие задания?

- Значит, в этих двух заданиях мы среди предложенных дробей «узнавали»,«признавали» правильные, а во 2 и 3, 5,6 заданиях подбирали дроби, удовлетворяющие определению. Именно такие два рода задач соответствуют тем двум назначениям определений, о которых мы с вами говорили ранее.

(Учитель организует фронтальную работу с классом над усвоением задачи № 951).

(выполняют задания фронтально с подробным обоснованием)

- Похожи задания 2 и 3, т.к. в них дроби требуется составить.

- В заданиях 1 и 4 дроби уже даны, требуется опредилить, являются ли они правильными или неправильными.

- В заданиях 5 и 6 нужно найти значение буквы, удовлетворяющее условию.

(Сделанные выводы заносятся в схему рыбы.)

• Прочитайте задание. Какие дроби надо написать?

- Какая дробь называется правильной?

- Чему равен знаменатель дроби?

• Каким должен быть числитель правильной дроби?

А в нашем случае меньше какого числа?

Запишите эти дроби.

№ 951(б) - выполните самостоятельно.

Правильные

Дробь, у которой числитель меньше

знаменателя называется правильной.

Знаменатель дроби равен 6.

Меньше 6.

; ; ; ;

Учащиеся выписывают все неправильные дроби с числителем 5. Затем осуществляется проверка полученных результатов.

Физкультминутка.

4. Выведение следствий из определения.

Но это ещё не всё, чем полезны определения. Сейчас мы в этом убедимся. Для этого обратимся к числовому лучу. Приложение 2.

- Назовите точки, которые лежат левее единицы.

Точки А и В лежат левее единицы.

- Какими дробями являются координаты этих точек?

Координаты этих точек - правильные дроби.

- Сравните их координаты с единицей.

Их координаты меньше единицы, так как они лежат левее.

- Какой вывод можно сделать? Сравните правильную дробь с единицей.

Любая правильная дробь меньше единицы.

- Как расположена дробь на координатном луче по отношению к единице?

Дробь совпадает с единицей, значит она равна единице.

- Какой дробью является координата точки С?

- Координата точки С - неправильная дробь.

- Назовите точки, которые лежат правее единицы?

- Точки D и Е лежат правее единицы.

- Какими дробями являются координаты этих точек?

- Координаты этих точек - неправильные дроби.

- Сравните их координаты с единицей.

- Их координаты больше 1, так как они лежат правее.

- Какой общий вывод можно сделать?

- Любая неправильная дробь больше или равна 1.

- А теперь сравните между собой правильную и неправильную дроби. Какой вывод можно сделать?

Любая правильная дробь меньше любой неправильной дроби.

- Те предложения, которые вы только что сформулировали в математике, называют гипотезами. Как вы получили эти гипотезы?

- мы сравнили несколько правильных дробей с 1, увидели, что все они меньше 1 и сформулировали свойство для дробей (аналогично для неправильных дробей).

- Данные гипотезы являются свойствами правильных и неправильных дробей.

Выдвинутые гипотезы в математике проверяют путём доказательства. Со схемой и сущностью доказательства мы познакомимся при изучении геометрии в 7 классе.

-Что нового вы узнали на данном этапе урока?

Свойства правильных и неправильных дробей. (заносим в схему рыбы)

5.Применение.

- А теперь применим полученные свойства к выполнению следующего задания.

Сравните дроби (приложение 1)

- Чем следует воспользоваться при выполнении данного задания?

Следует воспользоваться свойствами правильных и неправильных дробей.

- Сравните дробь с 1.

- Почему? <1.

<1.

Дробь правильная, а любая правильная дробь меньше 1.

- Сравните дробь с 1.

- Почему? правильная дробь меньше 1.

<1.

Дробь неправильная, а любая неправильная дробь больше 1.

Сравните дробь с 1.

Они равны, поэтому что дробь это целое, т.е. 1.

Во втором столбике выполните сравнение самостоятельно.

-А для чего нужны свойства правильных и неправильных дробей?

Учащиеся работают в тетрадях осуществляется самостоятельно. Затем проверка полученных результатов.

Они позволяют сравнивать правильные и неправильные дроби между собой, отмечать их на координатном луче. (заносим это в схему рыбы)

III. Рефлексивно - оценочная часть.

1. Подведение итогов.

- Итак, давайте подведём итог нашего урока.

- Что нового вы сегодня узнали на уроке?

Мы познакомились с правильными и неправильными дробями.

- Какую дробь называют правильной?

Правильной дробью называют такую дробь, числитель которой меньше знаменателя.

- Какую дробь называют неправильной?

Неправильной дробью называют дробь, числитель которой больше или равен знаменателю.

- Как называют такого рода предложения в математике?

Их называют определениями.

- Сравните правильную и неправильную дроби с 1. Какой вывод можно сделать?

Любая правильная дробь меньше 1, а любая неправильная дробь больше или равна 1.

- Итак, давайте посмотрим на схему, с помощью, которой мы получили новые знания.

- Как мы с вами открыли определение

правильной и неправильной дроби?

-Как получили свойства этих дробей?

Заслушиваются ответы учеников.

Учитель открывает этапы в заготовленной схеме:

Произвели классификацию дробей, сравнивая их числители и знаменатели

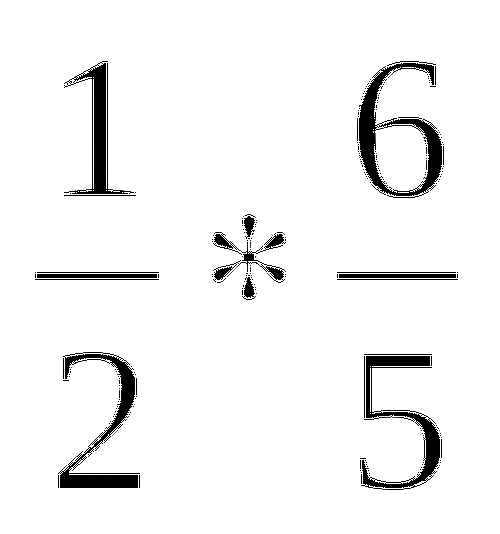
Сформулировали определения правильной дроби, неправильной дроби

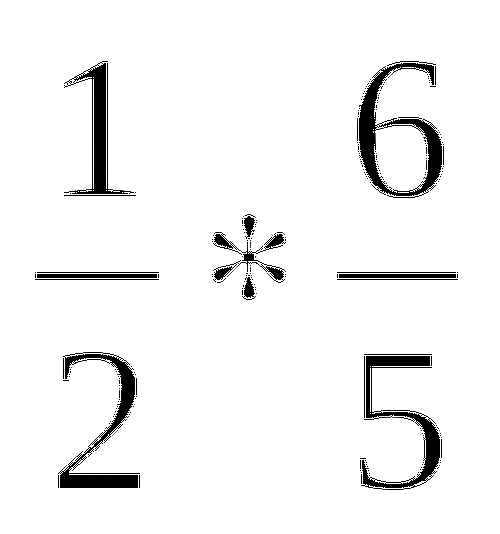
«Открыли» свойства правильных и неправильных дробей

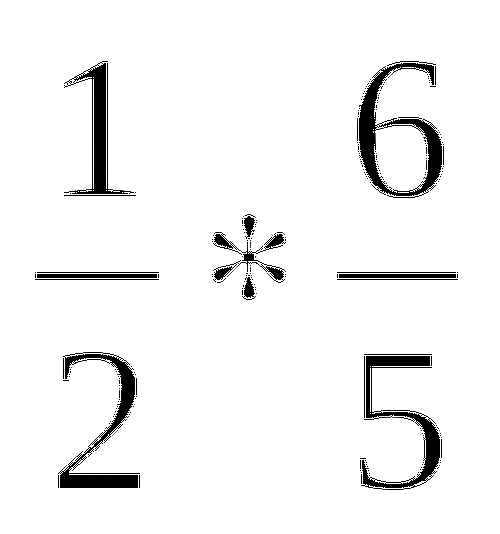
Применили полученные знания при решении задач

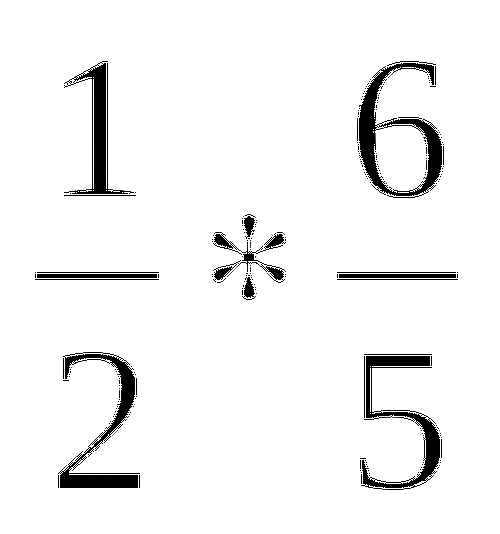
2. Самооценка деятельности на уроке.

(Заносим эту схему в хвост рыбы, как подведение итогов урока)

- Похожий путь открытия нового зна­ния проделывают ученые. Мы с вами сегодня на уроке попробовали себя в качестве ученых. Понравилось ли вам ощущать себя в такой непривычной роли? Какими качествами, по-вашему, должен обладать настоящий ученый? Какие из них вы почувствовали в себе? Какими вы хотели бы овладеть?

3. Задание на дом

1). Решить задачи №№ 951, 952, 975, 976.

2). Составить задачу на «узнавание» по определениям, изученном на уроке.

Домашнее задание комментируется, наиболее сложные задания и задания, в которых у учащихся возникли вопросы, подробно разбираются.

.

.

.

.

.

.

.

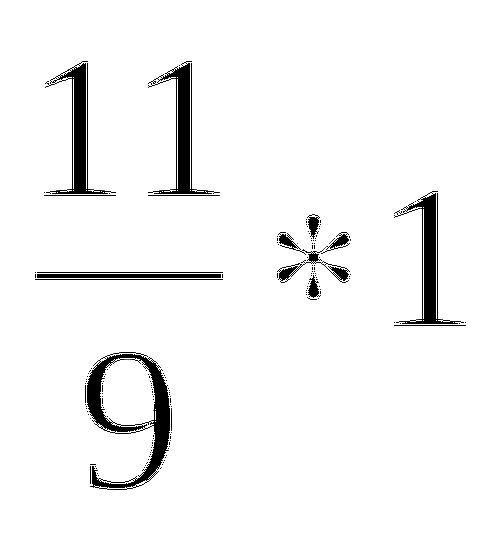
А

В

Д

С

Е

Х

0

1

Самоанализ урока.

Тема урока. Правильные и неправильные дроби. (Математика: Учеб. для 5 кл. сред. Шк./Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, СИ. Шварцбурд. - М: Просвещение. - пункт 25)

Тип урока. Урок изучения нового.

Цели урока.

В совместной деятельности с учащимися

1) Выявить содержание понятий правильной и неправильной дроби, используя методы классификации, аналогии, индукции и дедук­ции;

2) Смоделировать путь познания в математической науке на примере изучения понятий правильной и неправильной дроби.

Диагностируемые цели

Обучающие цели урока обеспечивают усвоение темы урока на уровне знания, понимания, применения.

В результате изучения темы урока ученик:

• знает и формулирует определения и свойства правильных и неправильных дробей;

• умеет использовать определение для выбора правильных (неправильных) дробей из числа предложенных;

• умеет приводить примеры и контрпримеры правильных и неправильных дробей;

• умеет сравнивать правильные (неправильные) дроби с 1, правильную дробь с не­правильной;

• имеет представление о строении родовидовых определений;

• знает о роли определений в математике, выделяет основные типы задач,
  решаемых на основе определений (приведение примеров и узнавание);

• умеет применять определения правильной и неправильной дроби к решению практических задач;

• выводит следствия из условия принадлежности объекта к данному понятию;

• указывает для решения каких задач можно использовать данное определение;

• составляет дидактические задачи на применение определения;

• различает определение правильной и неправильной дробей при обосновании хода решения задач;

• имеет представление о классификации как о приеме познания математических закономерностей.

Развивающие цели:

• Развивать познавательный интерес учащегося;

• Формировать вычислительную культуру учащихся;

• Развивать логическое мышление, то есть формировать умение наблюдать, выявлять закономерности, сравнивать и сопоставлять, проводить дедуктивные умозаключения.

Воспитательные цели:

• Ученик осознанно перерабатывает полученные знания для выработки целостной системы знаний по данной теме;

• Ученик формирует умения, организующие деятельность: постановка цели, и задачи, определение способов их реализации, планирование своих действий, реализующие действия и проверка результатов;

• Ученик развивает самостоятельность и добросовестность.

Структура урока.

I. Мотивационно-ориентировочная часть.

1. Актуализация имеющихся знаний и умений учащихся.

2. Создание проблемной ситуации, мотивация.

3. Постановка учебной задачи (цели) урока.
   П. Операционно-познавательная часть

(Содержательная часть).

1. Выделение существенных свойств понятия.

2. Моделирование определения.

3. Осознание определения и способов его получения.

4. Выведение следствий из определения.

5. Применение.

III. Рефлексивно-оценочная часть.

1. Подведение итогов урока.

2. Самооценка деятельности на уроке.

3. Постановка домашнего задания.

Основная цель мотивационно - ориентировочной части заключается в формировании у школьников смысла предстоящей деятельности, потребности у него в изучении нового учебного материала. Эта часть состоит из трёх связанных между собой этапов. Актуализация включает повторение тех опорных знаний, которые ведут непосредственно к новой учебной задаче. Опорным материалом для этого урока являются:1) знание понятий числитель и знаменатель дроби, правило сравнения дробей с одинаковыми знаменателями, определение понятий координатного луча и координаты точки на координатном луче, правило сравнения чисел с помощью координатного луча 2)умение отмечать точки с заданными координатами на координатном луче и определять координаты точек, заданных на координатном луче, умение сравнивать числа с помощью координатного луча.

Тема «Правильные и неправильные дроби» лежит в основе изучения последующей темы «Смешанные числа». Актуализация имеющихся у учащихся знаний, умений и навыков осуществляется в ходе фронтальной работы. На этом же этапе урока создаётся проблемная ситуация для подготовки учащихся к усвоению нового материала, когда учащийся не может воспользоваться правилом сравнения дробей с одинаковыми знаменателями, чтобы сравнить дроби с разными знаменателями, требуется искать другой способ сравнения этих дробей. Этап актуализации плавно переходит в этап мотивации. Цель этапов актуализации и мотивации в том, чтобы у ученика появилась потребность, желание и уверенность в своих силах. Этап мотивации заканчивается постановкой учебной задачи и планированием решения проблемной ситуации..

• Содержательная часть направлена на организацию деятельности учащихся, непосредственно связанной с решением учебной задачи. На этом этапе излагаются новые знания и способы действия, также здесь дети знакомятся с методологическим компонентом содержания математического образования, здесь впервые вводится на доступном учащимся уровне понятие определения, выделяются основные типы задач, решаемые на основе определений, формируется представление учащихся о классификации как о приеме познания математических закономерностей, вводится понятие гипотезы. На этом этапе у учащихся развиваются такие мыслительные операции, как: умение рассуждать, анализировать, сравнивать, делать выводы. Определение понятий правильной и неправильной дроби даётся через род и видовые отличия.

Правильной дробью называют:

1)дробь - род

2)числитель, которой меньше знаменателя - видовое отличие

Неправильной дробью называют:

1) дробь- род

2)числитель которой больше ее знаменателя или

3)равен знаменателю - видовое отличие

Видовые отличия задаются перечислением некоторого набора свойств. В ходе фронтальной работы с учащимися раскрывается роль определений в математике и выделяются типы задач, которые решаются на основе определений: подведение объекта под понятие, выведение следствий из условия принадлежности объекта к данному понятию. Далее в ходе фронтальной и индивидуальной работы учащихся осуществляется решение практических задач на основе применения определений понятий правильной и неправильной дроби. Затем учащиеся , используя правило сравнения дробей с помощью координатного луча, самостоятельно «открывают» и формулируют свойства правильных и неправильных дробей. Здесь осуществляется самостоятельная творческая, поисковая деятельность учащихся. Поэтому тип обучения на уроке проблемно - развивающий.

Большое значение имеет рефлексивно - оценочная часть. Её основная цель - осмысление проведённой учащимися математической деятельности, связанной с получением новых знаний. Подведение итогов урока осуществляется с помощью систематизирующей схемы, отражающей основные этапы и результаты данного урока.

На данном уроке была использована технология развития критического мышления- приём «фишбоун»(рыбный скелет). Стратегия «фишбоун» позволяет учащимся выявить причинно-следственные связи между новыми понятиями и способами их применения. Помимо этого данная схема позволяет систематизировать полученные знания, умения и навыки, понять их взаимосвязь.

На уроке использовались методы:

• Словесный - при формировании теоретических и практических знаний.

• Наглядный - для развития наблюдательности и повышения внимания.

• Репродуктивный - для формирования ЗУН, когда учащиеся готовы к проблемному изучению темы.

• Проблемно-поисковый - для развития самостоятельности мышления, материал не сложный, учащиеся готовы к проблемному изучению материала.

При планировании данного урока были учтены возрастные и индивидуальные особенности учащихся. Данный урок был проведён в одном из наиболее сильных классов, так как он включает в себя не только теоретический и практический материал, но и довольно обширный методологический компонент содержания. Это создаёт предпосылки для знакомства на доступном для пятиклассников уровне с процессом возникновения и развития понятия в математике.

Урок по теме «Правильные и неправильные дроби» является 11 уроком в главе «Дробные числа». Основная цель данной главы - выработать умение читать, записывать, сравнивать, выполнять основные арифметические действия с обыкновенными дробями. Определения понятия правильной и неправильной дроби на уроке вводится на основе общенаучных эмпирических методов научного познания таких, как: наблюдение, сравнение, анализ, синтез, обобщение, абстрагирование, конкретизация и систематизация. К открытию нового знания ученик приходит самостоятельно в процессе поисковой деятельности, он сам формулирует индуктивные умозаключения на основе использования общенаучных эмпирических методов научного познания. В основу урока заложен метод проблемного обучения, который направлен на самостоятельный поиск учащихся новых понятий и способов действия, предполагает последовательное и целенаправленное выдвижение перед учащимися познавательных проблем, разрешая которые, они под руководством учителя усваивают новые знания. Метод проблемного обучения обеспечивает особый способ мышления, оно становится гибким и творческим. Цикл проблемного обучения на данном уроке можно представить в виде следующей схемы:

Возникновение сущности затруднения

Осознания сущности затруднения

Выделение учебной проблемы

Выдвижение гипотезы её решения

Поиск способа решения

Решение

Выводы

Я считаю, что все поставленные задачи на уроке удалось реализовать. Урок цели достиг. Содержание заданий соответствует целям каждого этапа. На уроке были использованы как репродуктивный, так и проблемный типы метода обучения, которые позволяют учащимся самостоятельно открывать и формулировать определения и свойства правильных и неправильных дробей. На первых этапах отрабатывается умение действовать по образцу, а затем данное умение формируется в навык, когда учащиеся уже выполняют действие на подсознательном уровне. Все учащиеся на уроке были включены в активную деятельность. На этапе контроля усвоения знаний вопросы и задания соответствовали целям урока. На следующем уроке по данной теме следует организовать работу, направленную на отработку знаний, умений, навыков в процессе решения различного типа задач.