ТУЫНДЫНЫҢ КЕЙБІР ҚОЛДАНЫСТАРЫ

ТУЫНДЫНЫҢ КЕЙБІР ҚОЛДАНЫСТАРЫ

Дуан Гүлжанат Мұхтарқызы

Семей қаласының Шәкәрім атындағы мемлекеттік университетінің математика мамандығының 4 курс студенті

Қазіргі таңдағы ғылымның математиканың өнеркәсіпте, техникада және физикадағы қолданыстарына ерекше көңіл бөлетіні белгілі. Сондықтан механикалық және өнеркәсіптік есептерді шешуде туындының қолданылу ауқымы кең.

Біздің түсінуіміз бойынша, математиканы қолданбалы бағытта оқыту дегеніміз - математиканы оқытуда техника мен оған жақын ғылымдарда оны қолдану, халық шаруашылығы мен тұрмыста қолдануға бағыттау немесе оқытуға техникалық бағыт беру, яғни физика, химия, биология, география, сызу, технология сабақтары курсымен байланыс орнату, компьютерлік сауаттандыру, математикалық ойлау және жұмыс дағдысын қалыптастыру, оқушыны есептер шешуге, мысалдар шығартуға, оқушы өз бетінше есептей білу дағдысын қалыптастыру.

Туынды пәнаралық характерге ие болған математикалық ұғымның бірі. Физикада, теориялық физикада, жаратылыстану пәндерінде т.б пәндерде алғаш қолданыс тапқан.

Сол мақсатта туындының өндірісте және транспорт салаларында қолдануларын көрсетейік.

№1. Завод белгілі V көлемдегі консерві-қалбыр банкілерін шығарады. Қалбыр банкілерін дайындауға ең аз қаңылтар жұмсау үшін оның өлшемдері қандай болуы керек?

Шешуі: Қалбыр банкілері форма жағынан цилиндр болып келеді. Айталық цилиндрдің радиусы x, ал биіктігі h болсын. Есептің шарты бойынша бұл цилиндрдің көлемі 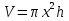белгілі. Бізді қызықтыратыны бұл цилиндрдің 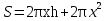толық беті, немесе 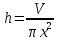екенін ескерсек,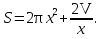

Сонда берілген есеп 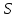ең кіші мәнді қабылдайтын 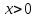мәндерін табу керек. ( 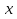берілген цилиндрдің радиусы, сондықтан ).

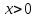Ол үшін бұл функцияның монотондылық аралықтарын табамыз.

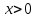
Бұдан көретініміз, 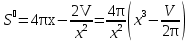аралығында функция кемиді. Себебі мұнда, 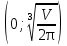ал 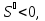аралағында функция кемиді. Себебі мұнда 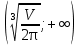Ендеше 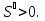бұл функция ең кіші мән алады. Биіктік 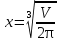екен.

Сонымен қалбыр банкісіне ең аз қаңылтыр жұмсау үшін, оның биіктігі диаметріне тең болуы керек болып шықты.

Транспортта қолдану. Автомобиль жолдарының айырықтарының проекцияларын салуда және олар арқылы тарайтын (өтетін) жолдарының есебін жүргізуде комплексті түрде экономикалық және географиялық жағдайларының, ең бірінші алдын-ала адамдардың жұмыс уақытының шығынын, әкелуге апаруға кеткен шығын соған қоса төмендегі есепті шығаруға тура келеді.

№2. Егер үлкен АВ жолының бойындағы машинаның қозғалыс жылдамдығы 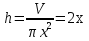, ал қосылушы СЕ жолдың бойындағы көліктің жылдамдығы 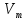(мұндағы 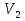) болса, АЕС маршруты бойынша қозғалған машинаның шығын жолдардың қосылу бұрышы 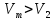қандай болғанда ең аз шама болады?

Шешуі: (1-сурет) С -нүктесінен АВ-ға СD- перпендикулярын жүргізіп 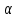деп белгілейміз, ал АD-ны 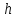деп белгілесек,

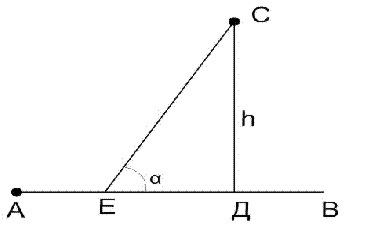
1-сурет

Бұдан АЕС маршруты бойынша қозғалған машинаның уақытын табамыз.

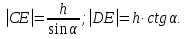
Жолдың бағытын анықтау үшін, мұндағы А нүктесі белгіленгендіктен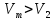

шамасы 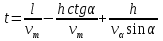аралығында өзгере алады. Есеп берілген аралықта - 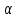функциясының ең аз шамасын анықтауға бағытталған. Туындысын табамыз:

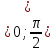
Мұндағы 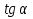болғандықтан, қарастырылып отырған туынды тек бір нүктеде нөлге айналады.

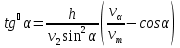
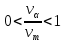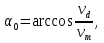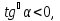Олай болса егер және егер 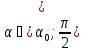байқайтынымыз t функциясы және 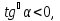егер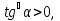

Бұл дегеніміз 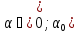аралығында t функциясы кемиді, ал 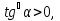аралығында өседі.

Сондықтан зерттелініп отырған t функциясы 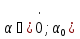болғанда ең аз мәнге ие болады.

Жауабы: Жолдардың қосылу бұрышы 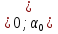теңдікпен есептеледі.

Қорыта айтқанда оқушыларда математикаға деген қызығушылығын туғызу, математиканың қажеттілігін түсіндіру үшін болашақ математика пәнінің мұғалімі ретінде өмір қажеттігінен туындайтын есептерді кеңінен қолдану қажет.

Пайдаланылған әдебиеттер:

1. Тұрбаев Б.Е., Қанибайқызы Қ. Дифференциалдық және интегралдық есептеулер негіздері. Оқу құралы - Қызылорда, Қызылорда-Қанағаты, 2013- 152 б.

2. Тұрбаев Б.Е., Бедерова Қ., Әжібекова Г. Математиканы практикалық бағытта оқытудың алғашқа негіздері / Математика және физика ғылыми-әдістемелік журналы 2013.- №1. 2-3б.