Занятие по теме «Решение уравнений, неравенств, построение графиков функций и зависимостей, содержащих переменную под знаком модуля»

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа № 1»

Предметный курс по выбору «МОДУЛЬ»

Занятие по теме «Решение уравнений, неравенств, построение графиков функций и зависимостей, содержащих переменную под знаком модуля»

Подготовила

учитель математики МОУ «Средняя общеобразовательная школа №1» Миргородова Татьяна Геннадьевна

Курск 2008

Тема занятия: Решение уравнений и неравенств, содержащих переменную под знаком модуля. Построение графиков функций, содержащих модуль.

Цель занятия:

-обобщить знания и умения решать определённый класс уравнений и неравенств, содержащих переменную под знаком модуля; навыки построения графиков функций и зависимостей, содержащих модуль;

-развивать креативное мышление;

-воспитывать толерантность, коллективизм, взаимопомощь.

План занятия:

1. Орг. этап - 2 мин.

2. Информационный ввод - 5мин.

3. Выступление - отчет творческих групп о проделанной работе над проектом - 15 мин.

4. Решение уравнений и неравенств, построение графиков с использованием материалов творческих групп - 15 мин.

5. Итог коллективного занятия - 3 мин.

На занятия приглашаются учащиеся 8 классов, которые выступают в роли обучающихся.

Ход занятия.

1. Орг. этап - 2 мин.

2. Информационный ввод-3 мин.

Задания с модулями уже многие годы предлагаются на вступительных экзаменах по математике, в том числе среди заданий единого государственного экзамена. И как показывает практика, эти примеры вызывают трудности у значительной части школьников. Изучение модуля начинается в 6 классе, затем эту тему мы рассматриваем в 8 классе. Материала по данной теме недостаточно, а если он есть, то рассчитан на учащихся 10-11 классов. Целью нашего курса было создание методички, которой могли бы пользоваться учащиеся 8 классов при изучении данной темы. Сегодня наше занятие посвящено отчёту творческих групп о проделанной работе. Каждая группа выбрала направление в работе, которое ей показалось наиболее интересным. На нашем занятии присутствуют и учащиеся 8 класса, которые выступают в роли обучающихся. Сначала, мы выслушаем выступление творческих групп, а затем ребята 8 класса под руководством своих наставников попробуют выполнить те задания, которые им покажутся наиболее интересными.

3. Выступление - отчет творческих групп о проделанной работе над проектом - 15 мин.

1. Понятие модуля.

Модулем действительного числа (абсолютной величиной числа х) называют само это число, если х ≥ 0, и противоположное число, если х < 0.

Из определения следует, что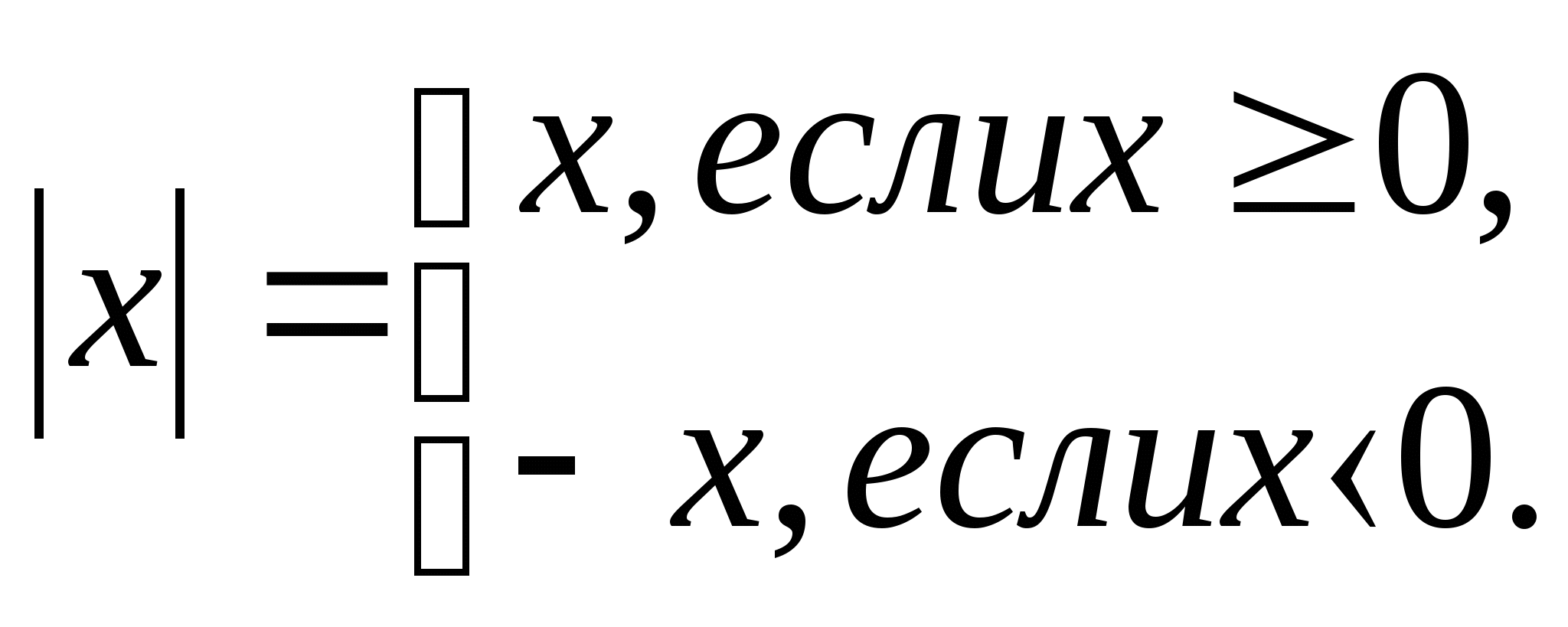

Геометрически означает расстояние на координатной прямой от точки х до 0.

Расстояние между точками х и b координатной прямой равно , т.е. =

Пример 1.

Расстояние между точками х и 1 на координатной прямой равно 2. Этими точками являются х₁ = 3, х₂ = -1.

Пример 2. > 2

Расстояние между точками х и 1 больше 2, т. е.

Пример 3. ≤ 2

Расстояние между точками х и 1 не больше 2., т.е

Таким же образом можно решать и более сложные уравнения:

,

Например:

2. Уравнения, содержащие переменную под знаком модуля.

В своём проекте мы рассматриваем методы решения уравнений, содержащих переменную под знаком модуля. Чтобы решить такие уравнения, надо освободиться от знака модуля. Рассмотрим несколько случаев.

а)

Решением является объединение решений двух систем:

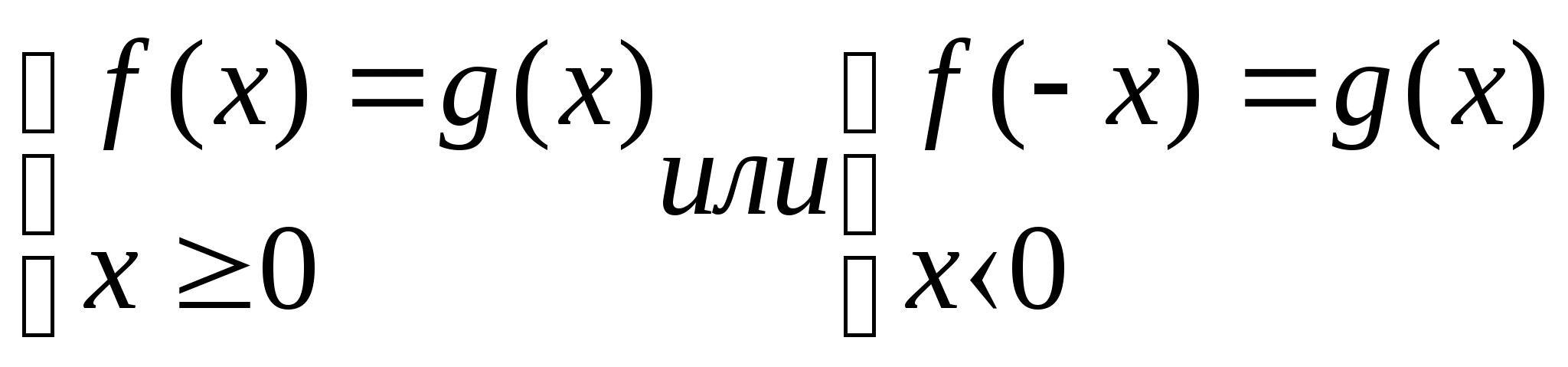
Решить уравнение:

1 способ

Используя определение модуля имеем

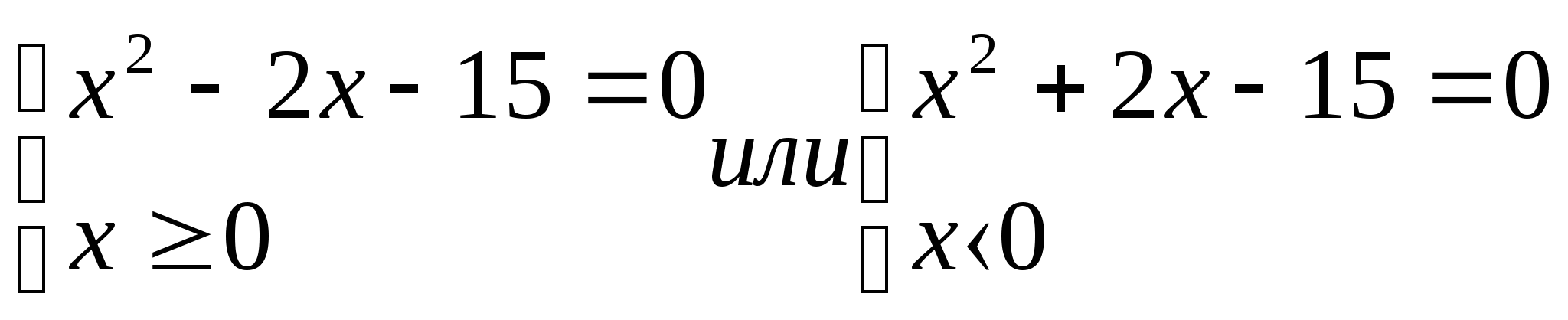
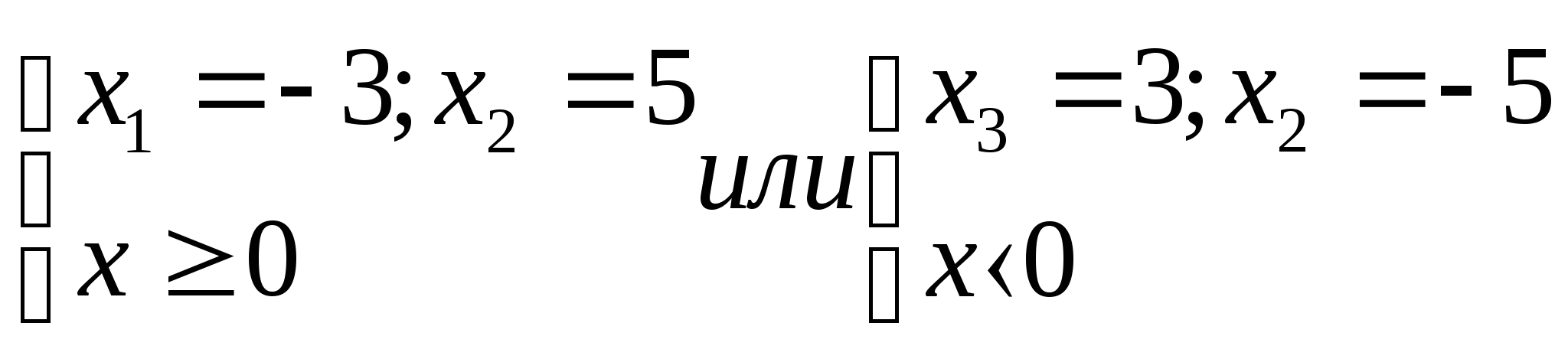
х= ± 5.

Ответ: ± 5.

2 способ Данное уравнение можно решить, используя метод замены переменой. Пусть = у, тогда данное уравнение примет вид: у² - 2у - 15 = 0 (т.к. х² = ²) Решая его , получаем корни у₁= - 3; у₂ = 5.Возвращаясь к замене, получим = -3 или = 5. первое уравнение корней не имеет, а второе имеет два корня -5 и 5.

б)

Если:

а < 0 , то данное уравнение не имеет корней;

а = 0, то данное уравнение равносильно уравнению f(x) = 0;

a > 0, то

или

Решить уравнение:

х² - 2х - 7 = 4 или х² - 2х - 7 = - 4

х² - 2х - 11 = 0 х² - 2х - 3 = 0

х_1,2 = х₃ = -1; х₄ = 3.

Ответ: ; - 1; 3.

в)

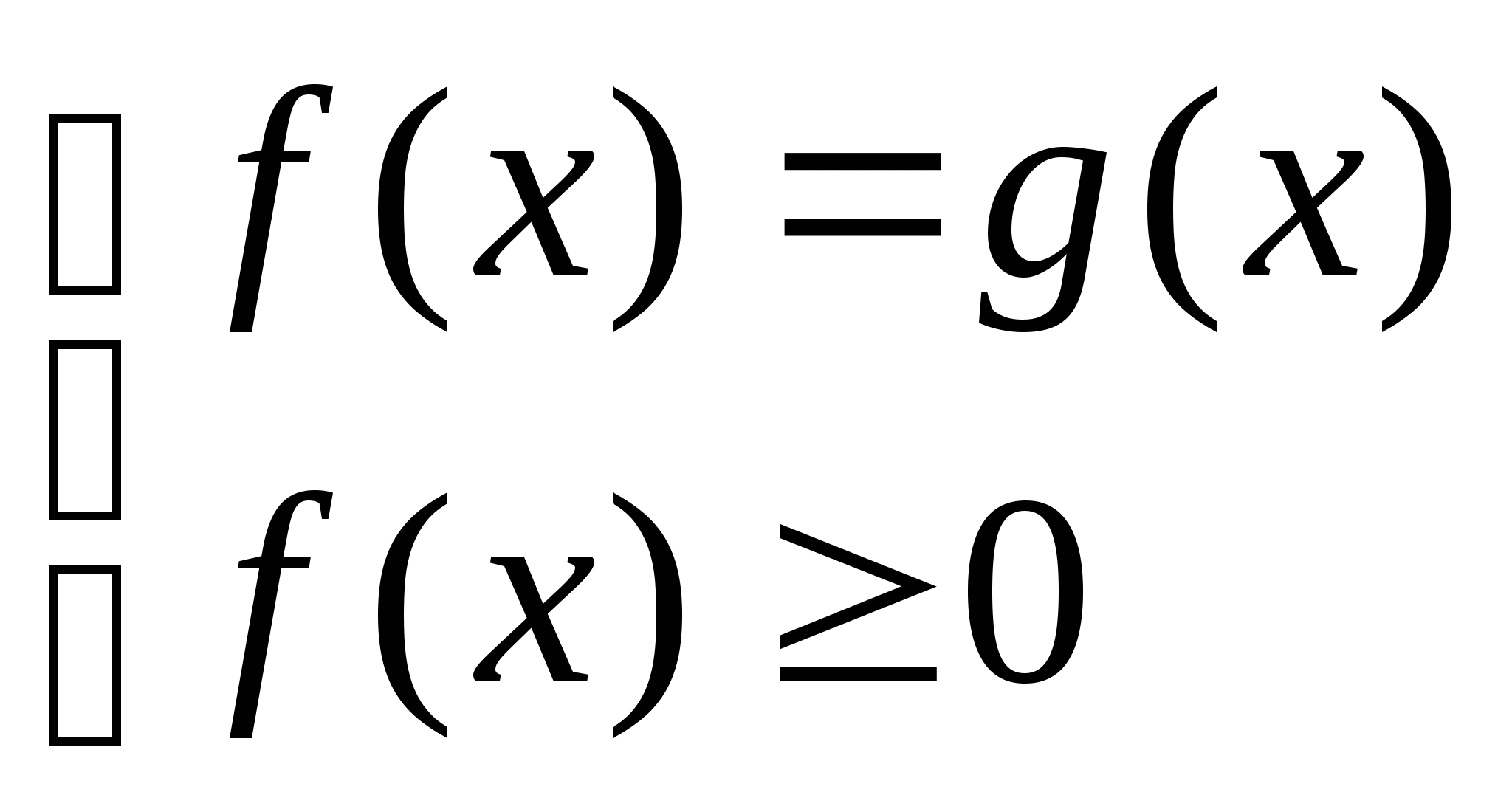или

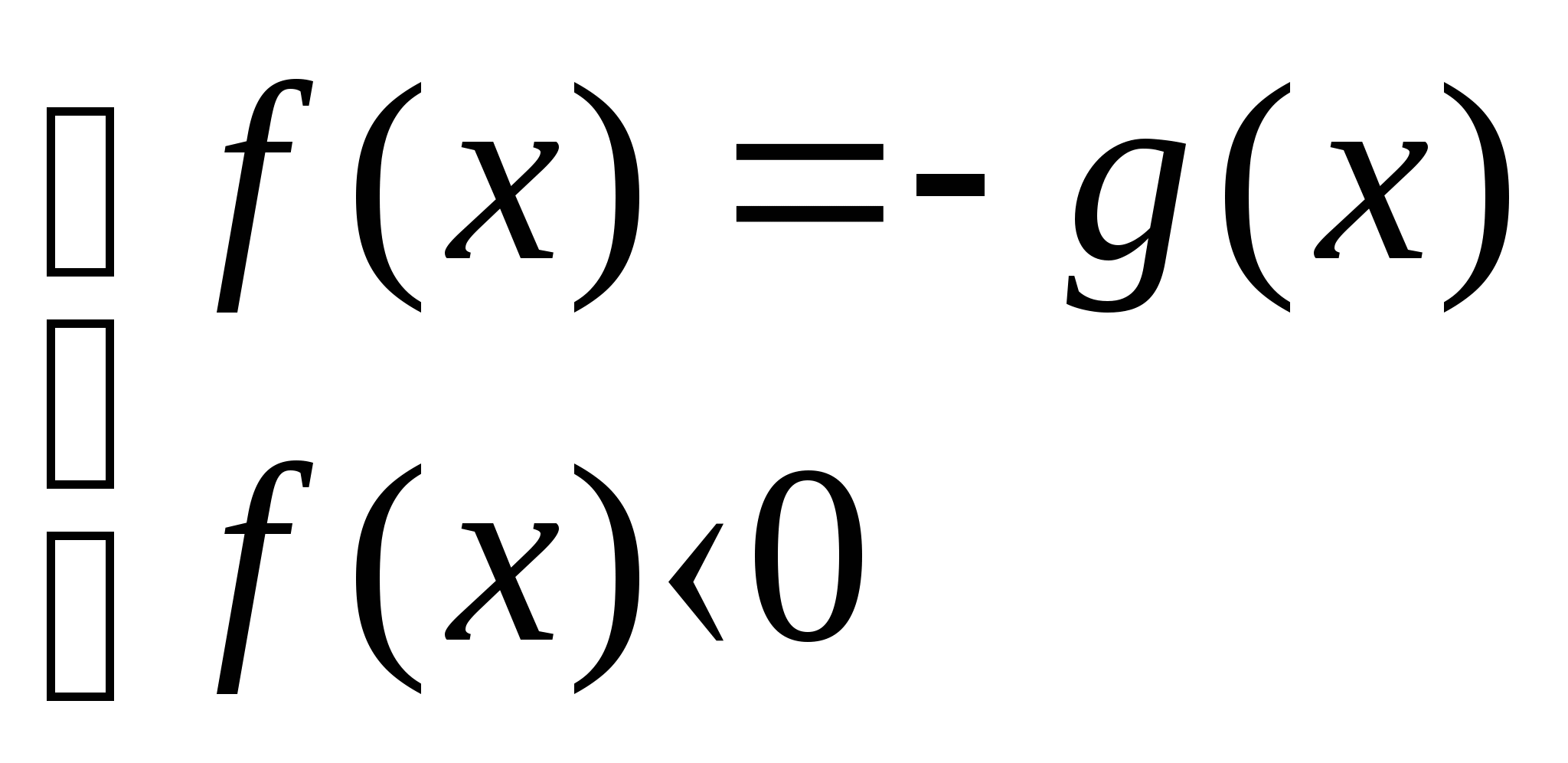
Решить уравнение

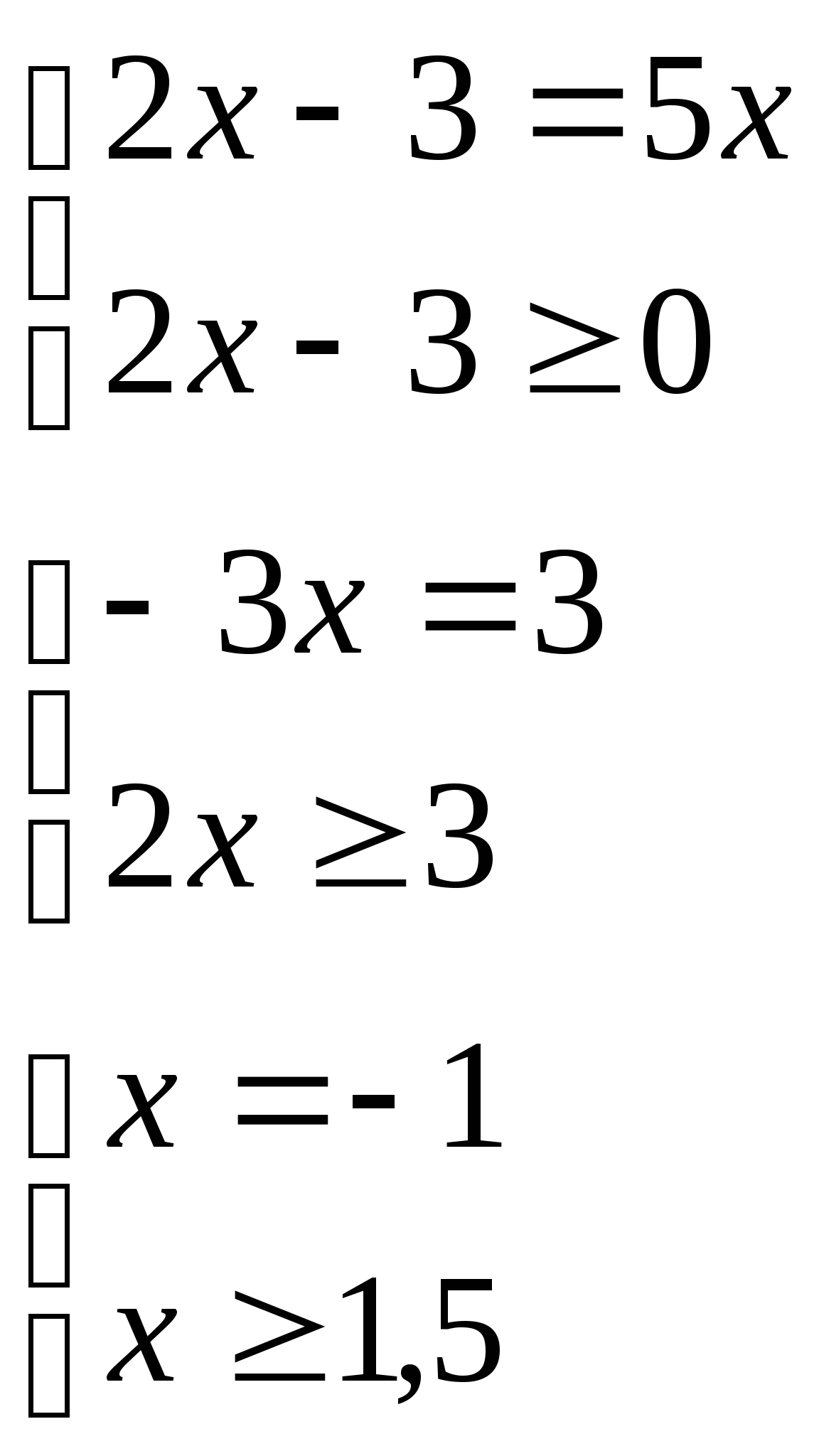или

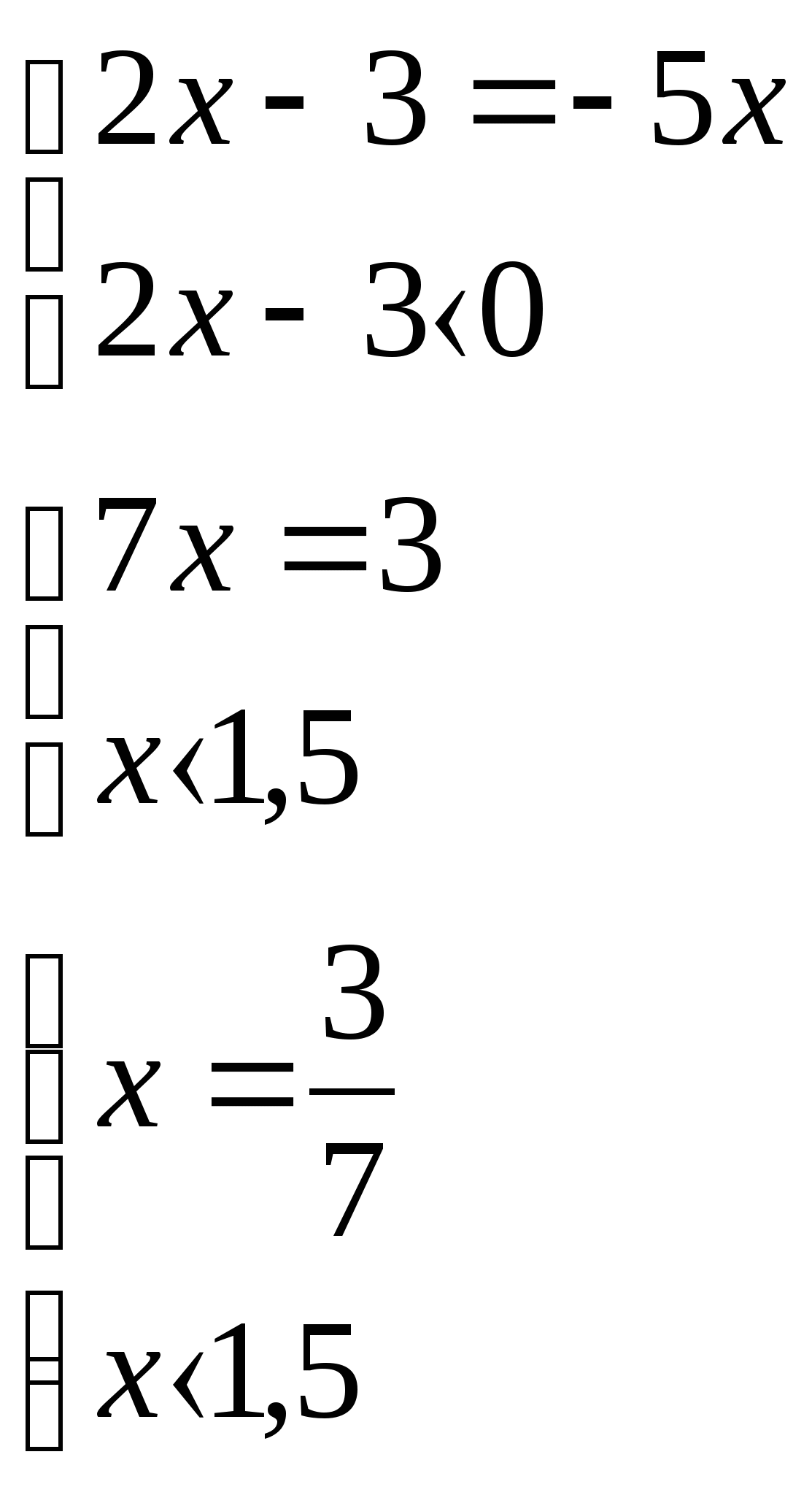
Ответ:.

3. Неравенства, содержащие переменную под знаком модуля

а), где а > 0 равносильно двойному неравенству -а ≤ f(x) ≤ а,

если а = 0 , то равносильно уравнению f(a) = 0.

Пример:

-2< х-1 < 2

-2 +1 < х < 2+1

-1 < х < 3.

Ответ:( -1;3)

б) , где а ≥ 0 равносильно неравенствам:

f(x) ≥ a или f(x) ≤ -a

Пример:

2х + 5 ≥ 7 или 2х + 5 ≤ -7

2х ≥ 2 2х ≤ - 12

х ≥ 1 х ≤ -6

Ответ:

4. Построение графиков функций, содержащих знаки модуля.

а)

Для построения графика данной функции необходимо изобразить график функции у = f(x) после чего часть графика, лежащую выше оси абсцисс и на ней, оставить неизменной, а часть графика, лежащую ниже этой оси, заменить ее образом при симметрии относительно оси абсцисс.

б)

Для построения графика данной функции надо взять часть графика функции у = f(x), лежащую в полуплоскости х ≥ 0, симметрично отобразить её относительно оси у и объединить получившиеся множества.

в)

Для построения данного графика достаточно применить алгоритм построения графика функции , а потом функции , или наоборот.

г)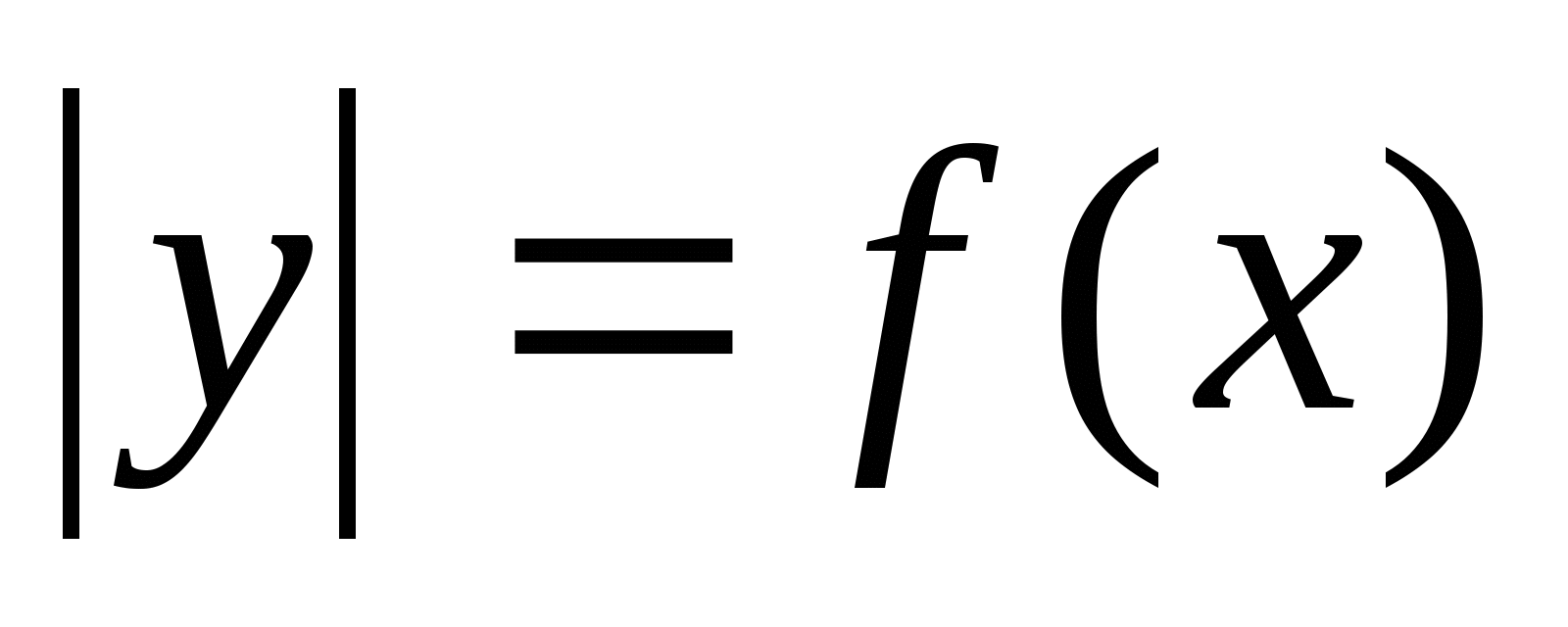

Для построения графика данного уравнения необходимо ту часть графика уравнения у = f(x) , которая лежит выше оси абсцисс и на ней симметрично отобразить относительно оси х и объединить получившиеся множества. Данную зависимость между переменными х и у, выраженную данным равенством нельзя отнести к функциональной. Именно в таких случаях надо говорить об уравнении, а не о функциях.

4. Решение уравнений и неравенств, построение графиков с использованием материалов творческих групп - 15 мин.

А каждая творческая группа предлагает ряд заданий, которые предлагается решить учащимся 8 классов с использованием их рекомендаций.

Задания для себя дети выбирают свободно, те, которые им понравятся.

Консультанты каждой творческой группы активно помогают учащимся 8 классов. После выполнения 8-классниками нескольких заданий консультанты показывают учащимся красивые графики и соответствующие уравнения.

Задания для работы

Решить уравнения используя геометрическое определение модуля

1.

2.

3.

4.

Решить уравнения

1.

2.

3.

4.

5.

Решить неравенства

1.

2.

3.

4.

Построить графики уравнений, содержащих переменную под знаком модуля

1.

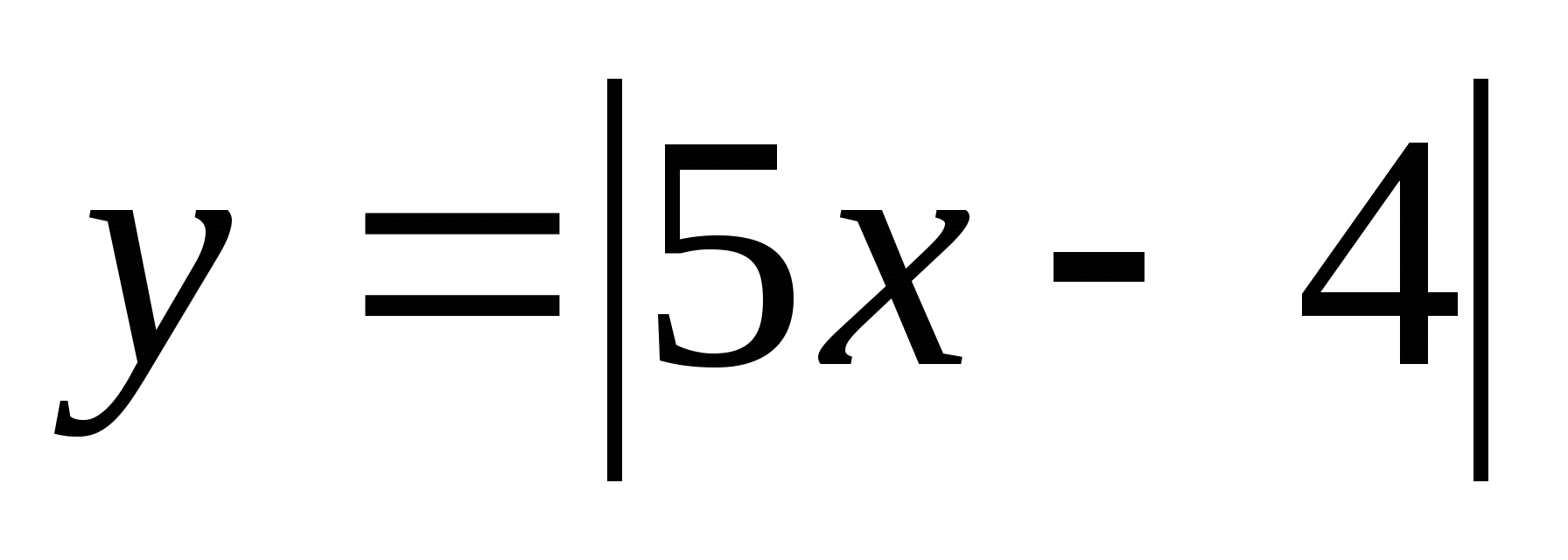
2.

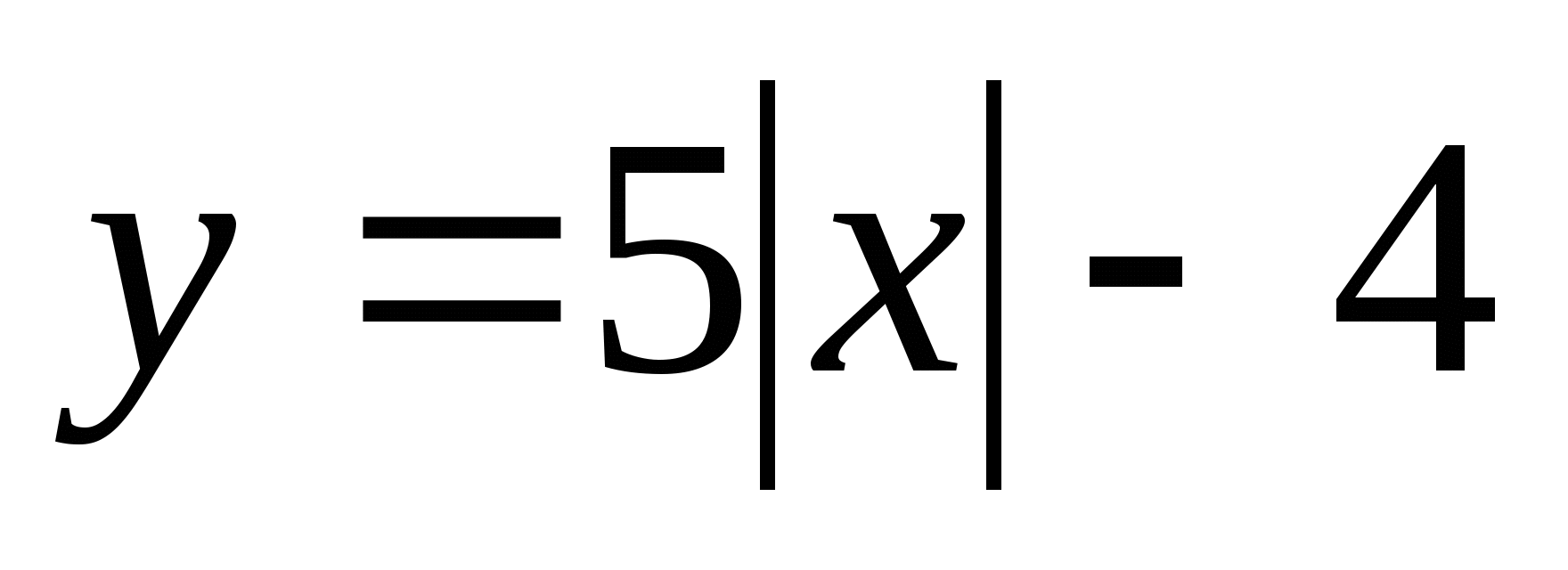
3.

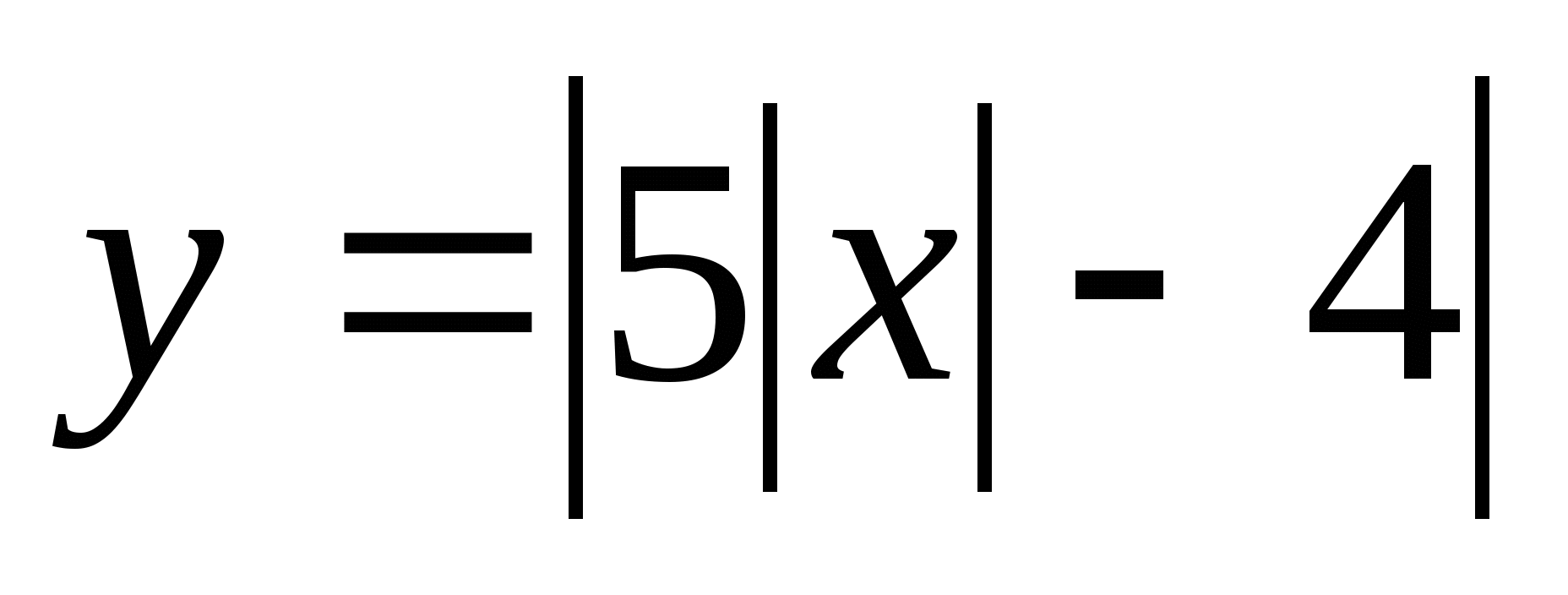
4.

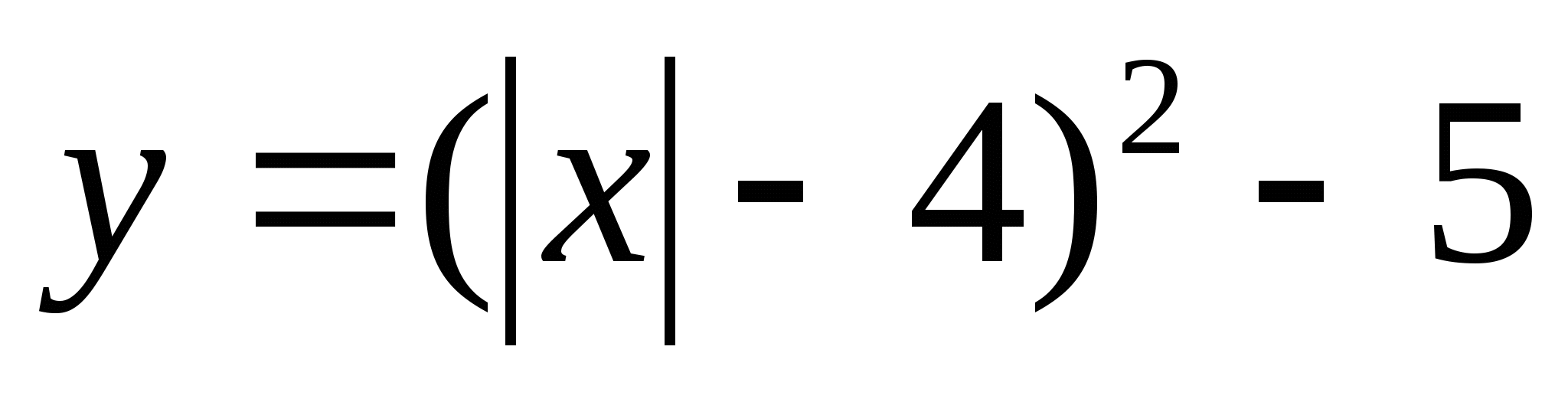
5.

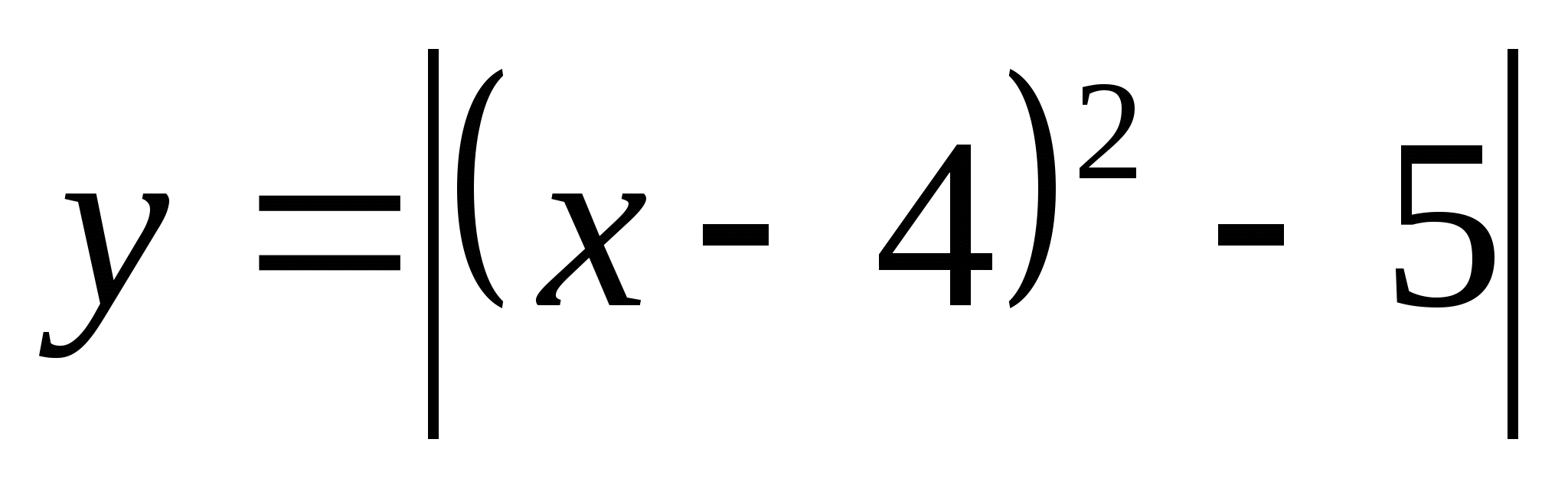
6.

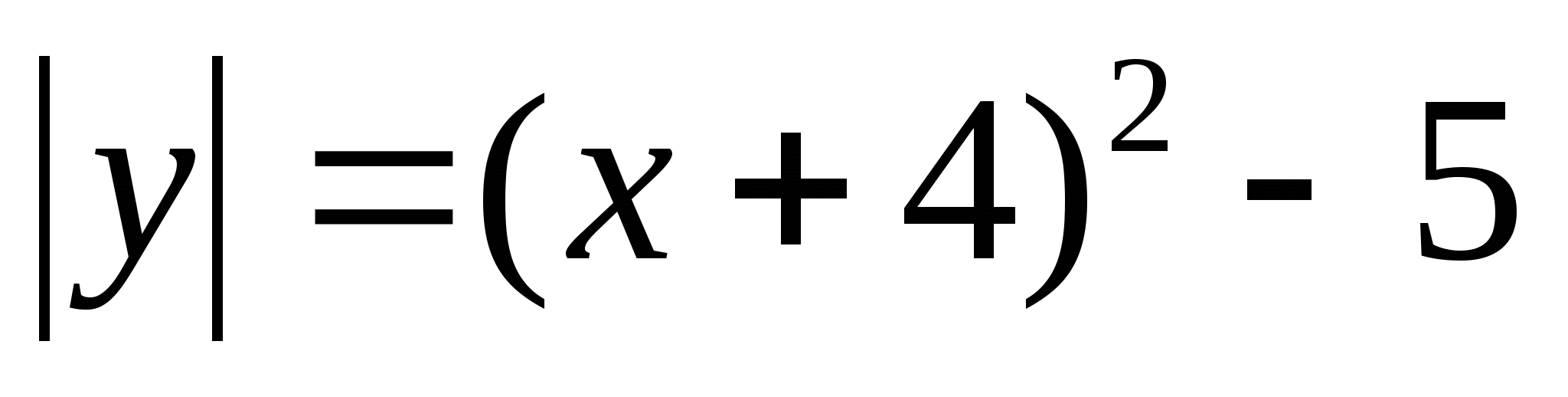
6. Итог занятия.

9