конспект по алгебре на тему'Квадратные уравнения' (8 класс)

Урок математики в 8 классе.
Тема урока

«Квадратные уравнения»

Кузина Тамара Сергеевна,

учитель математики МБОУ «Малоскуратовская оош»

Чернского района Тульской области

2013-2014 уч год.

Цели урока:

Образовательные цели урока:

- Решение квадратных уравнений по формуле

-Развитие приемов умственной деятельности, логического мышления, памяти, внимания, умения сопоставлять, анализировать, делать выводы.

Обратить внимание учащихся на решение квадратных уравнений, в которых а +b + с = 0;

- Привить навыки устного решения таких уравнений.

Воспитательные цели урока

*способствовать эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений

* Воспитание чувства ответственности, взаимопонимания, взаимоподдержки, уверенности в себе;

• Развивающие

*развивать воображение, пространственные представления, уметь действовать по заданному алгоритму и конструировать новое;

*при решении задач развивать творческие и прикладные стороны мышления;

*вырабатывать умение формировать, обосновывать и доказывать свои суждения.

Тип урока: урок закрепления

Формы работы с учащимися: коллективная. Работа в парах, индивидуальная.

Оборудование: компьютер, учебник, раздаточный материал. Презентация по теме «Квадратные уравнения»

План урока:

1. Организационный момент: настрой на рабочий лад; сообщение темы урока; сообщение плана урока.

2. Презентация по теме: "Решение квадратных уравнений "

3. Повторение. Устные упражнения

4 Изучение свойства коэффициэнтов квадратного уравнения Отработка алгоритма решения квадратных уравнений в тетрадях.

5. Исторические факты. Решение задачи XII века Бхаскара.

6.Тест./самопроверка/.

7.Подведение итогов урока, домашнее задание.

Рефлексия

Творческое задание

Итог урока.

На доске запись: Эпиграф: Если ты услышишь, что кто-то не любил математику ,не верь. Ее нельзя не любить - ее можно только не знать.

Ход урока

1. Организационный момент

*У. Начать сегодняшний урок мне хотелось бы следующим высказыванием: «Посредством уравнений, теорем, я уйму всяких разрешал проблем…»

Это слова английского поэта средних веков. Как вы думаете, о каком математическом понятии пойдет речь на уроке?

Учащиеся ( об уравнении).

*У. Верно.

Тема урока «решение квадратных уравнений» формуле, используя алгоритм решения . Откроем свойство коэффициэнтов квадратного уравнения.

2.Актуализацииия темы

Учитель

ученик

1

Вы каждый урок приветствуете меня вставанием. А как еще приветствуют люди друг друга ?

Кивают головой, машут рукой. Целуют руку, целуются. Обнимаются.

Жмут друг другу руки

Слайд Нестандартная задача Решаем вместе

Участники семинара обменялись рукопожатиями, и кто-то подсчитал, что всех рукопожатий было 66. Сколько человек явилось на заседание?

Слайд Решение задачи

Пусть Χ-число участников заседания. Тогда каждый из Χ участников пожал (Χ-1) руку. Значит, всех рукопожатий должно быть Χ(Χ-1).

Надо помнить, что когда один из участников заседания пожимает руку другого, то и этот другой пожимает руку первого. Поэтому эти два рукопожатия следует считать за одно.

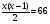Число пересчитанных рукопожатий вдвое меньше, нежели Χ(Χ-1).

Составим уравнение:

.

x²-x-132=0 .D= b² - 4ac=1 -4*1*(-132)=529 -11 не подходит по смыслу задачи x=-11, x =12.

Ответ: В заседании участвовало 12 человек

Учитель: Как видите, мы только успели попреветствовать друг друга , а квадратные уравнения уже присутствуют здесь. Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных, уравнений и неравенств.

III.Повторение

Задание1.

Слайд Слайд-проверка ( Оценить 2б)

Слайд Задание 2

Какое уравнение называется квадратным? (Оценить 2б)

Ответ: (Б) ученик выбирает уравнение и объясняет: какое это уравнение?

Что значит решить уравнение? Что называется корнем уравнения7

Задание 3 (Оценить 2б)

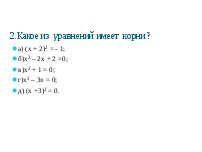
Ответ Г)и Д) учащиеся выбирает задание объясняютсвои ответы

**************************************************************************

IV. Исследование свойств коэффициентов квадратного уравнения.

Учитель: . При решении некоторых квадратных уравнений , оказывается ,немаловажную роль играет сумма коэффициентов

Слайд Задание 1.

1. Найдите корни уравнения и сумму коэффициентов.

1. х² + 2х - 3 = 0;

2. х² + х - 2 = 0;

3. х² - 3х + 2 = 0;

4. 5х² -8х + 3 = 0;

(Учащиеся решают уравнения и заполняют таблицу (на доске))

Слайд 2. Проверка

сумма

корни коэффициентов

х² + 2х - 3 = 0; х₁ = 1; х₂ = -3 0

х² + х - 2 = 0; х₁ = 1; х₂ = -2 0

х² - 3х + 2 = 0; х₁ = 1; х₂ = 2 0

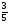5х² -8х + 3 = 0; х₁ = 1; х₂ = 0

Учитель: Сравните суммы коэффициентов. Ученик: Суммы коэф. равны

Что заметили? Нулю

Учитель: Сравните корни. Что заметили? Ученик: Уравнения имеют равные

Корни:х=1.,и х=с/а

Слайд Вывод

ах² + bx + c = 0;

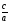a + b + c = 0;

x₁ = 1; x₂ =

(если а = 1, то х₁ = 1; х₂ = с).

******************************************************************

V.Решение задач на закрепление свойства

Задание1. Работа по учебнику

Задание2.

********************************************************************

Физкультминутка

************************************************************************

Слайд

VI Работа в парах ГИА

Учащиеся решают в парах, а затем один ученик объясняет у доски

VII. Решение квадратных уравнений по формуле

Деффиринцированная работа Карточки

Задание 1.

Взаимопроверка Оценить (2б)

Решите уравнение у доски

а) 7 х² - 9х + 2 = 0. * б) х² + 12=7х

в) (х-2)² + 24=(2+3х)² г)2х² +х/5 =4х-2/3

****************

Сообщения учеников

VIII.История возникновения квадратных уравнений.

Слайд Индия. Задачи на квадратные уравнения встречаются уже в 499 году В Древней Индии были распространены публичные соревнования в решении трудных задач В одной из старинных индийских книг говорится по поводу таких соревнований следующее; Как солнце блеском своим затмевает звезды так ученый человек затмит славу другого в народных собраниях предлагая и решая алгебраические задачи» Часто они были в стихотворной форме

Слайд Вот одна из задач знаменитого индийского математика XII века Бхаскара

Обезьянок резвых стая,
Всласть поевши, развлекалась.
Их в квадрате часть восьмая,
На поляне забавлялась,
А двенадцать по лианам
Стали прыгать, повисая…
Сколько ж было обезьянок,
Ты скажи мне в этой стае?

Слайд Решение:

Пусть было x обезьянок, тогда на поляне забавлялось - (x/8)2.

Составим уравнение:

(x/8)2+12=x;

X2/64-х+12=0

x2-64х+768=0

D=1024

x1=16, x2=48

Ответ:16 и 48.

Слайд

Слайд Тест .Тема «Решение квадратных уравнений по формуле» Оценить

Инструкция: выберите один ответ из предложенных.

1. Какое из квадратных уравнений является полным:

А) 5х²=0 Б) 8-2х+3х²=0 В) 7х²+1=0 Г) 6х-х²=0

2. Дискриминант квадратного уравнения х²+5х-6=0 равен:

А) 0 Б) 49 В) 1 Г) 16

3. Сколько корней имеет квадратное уравнение х²+6х+9=0

А) 1 Б) 2 В) нет корней Г) определить невозможно

4. Решите уравнение х²-2х-15=0

А) корней нет Б) 3; -5 В) 1 Г) 5; -3

5. Решите уравнение 3х²-3х+4=0

А) 1 Б) 0; 4 В) корней нет Г) 0,5

6. Найдите наибольший корень уравнения -х²-5х+14=0

А) 2 Б) 7 В). 38 Г) корней нет.

Слайд Таблица верных ответов

№ задания

1

2

3

4

5

6

1 вариант

Б

Б

А

Г

В

А

Оценка ; 4верныхответа-3б, 5 верных ответов- 4б, 6 верных ответов---5 баллов

Слайд

VII. Рефлексия

Подведение итогов урока.

Творческое задание Квадратное уравнение, содержащее модуль.

Решите уравнение:

I х²-3х+4 I = I 2х-2 I