- Учителю
- Урок по математике Теорема Пифагора
Урок по математике Теорема Пифагора
Урок по математике
8 класс
Учитель математики
Текинского филиала МБОУ «Сатинская СОШ»
Фирсова Надежда Константиновна
Урок по математике в 8 классе
Решение задач по теме «Теорема Пифагора»
Цели урока: формировать знания, умения и навыки при решении задач по теме «Теорема Пифагора», развивать логическое мышление при решении задач.
Тип урока: формирование знаний, умений и навыков.
Структура урока:
I Орнмомент
II. Фронтальный опрос
-
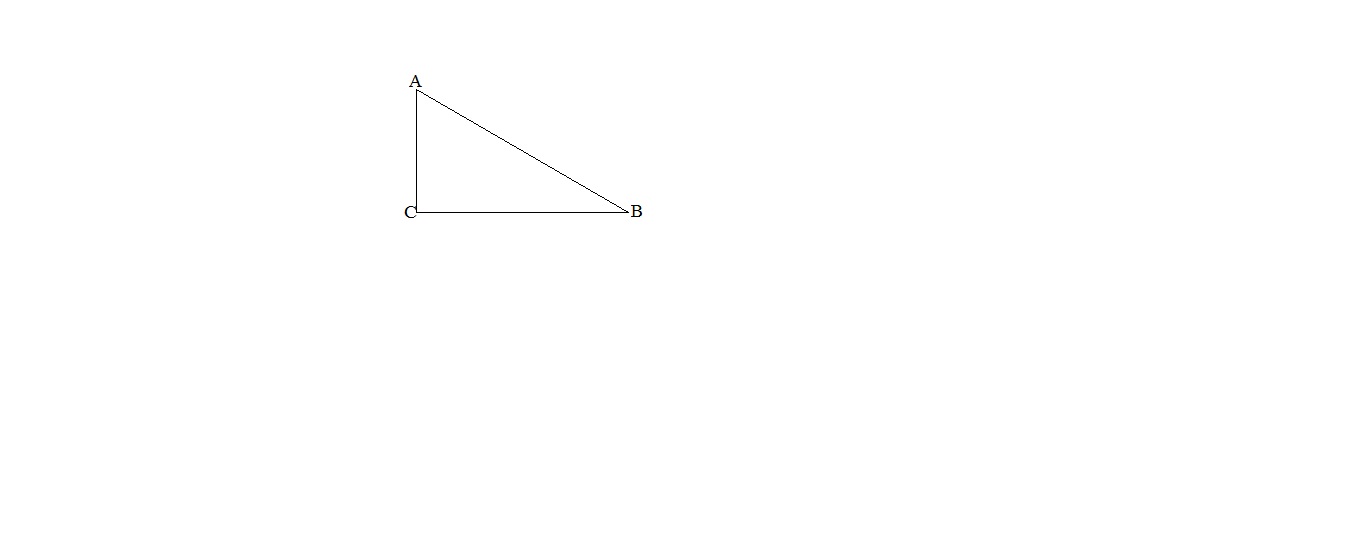
Что называется косинусом угла? Чему равен cos A, cos B?
-
Сформулируйте теорему Пифагора.
-
Назовите следствия из нее.
Прочитать стихотворную формулировку Пифагора.
«Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем.
Катеты в квадрат возводим,
Сумму степеней находим-
И таким простым путем
К результату мы придем!»
III Задачи по рисункам (устно)
-
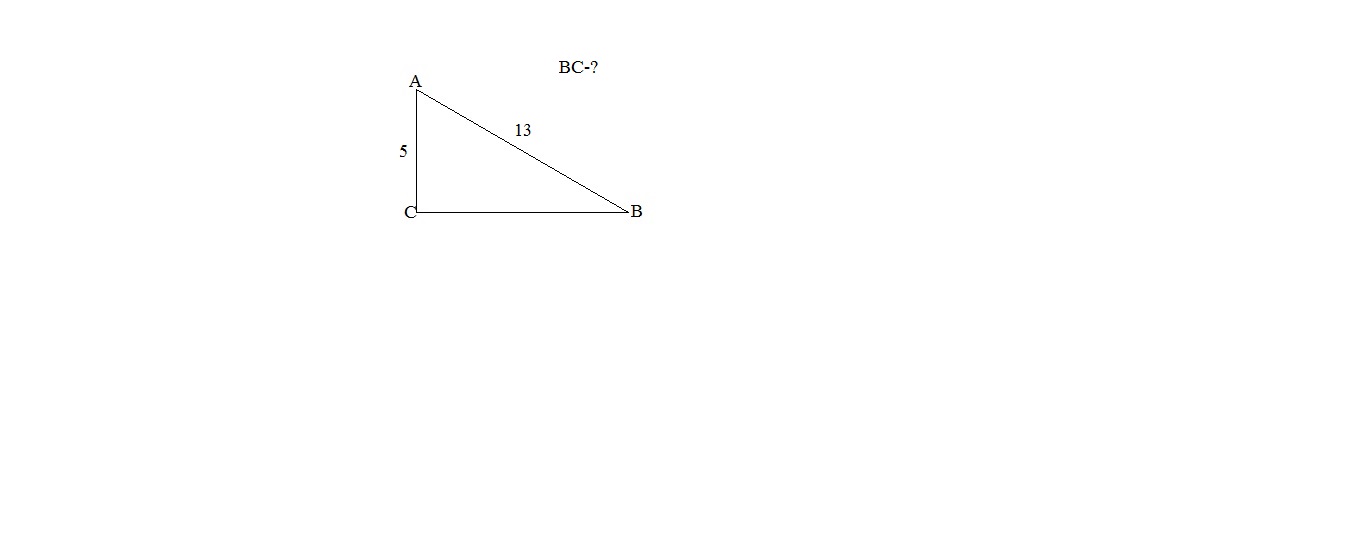
-
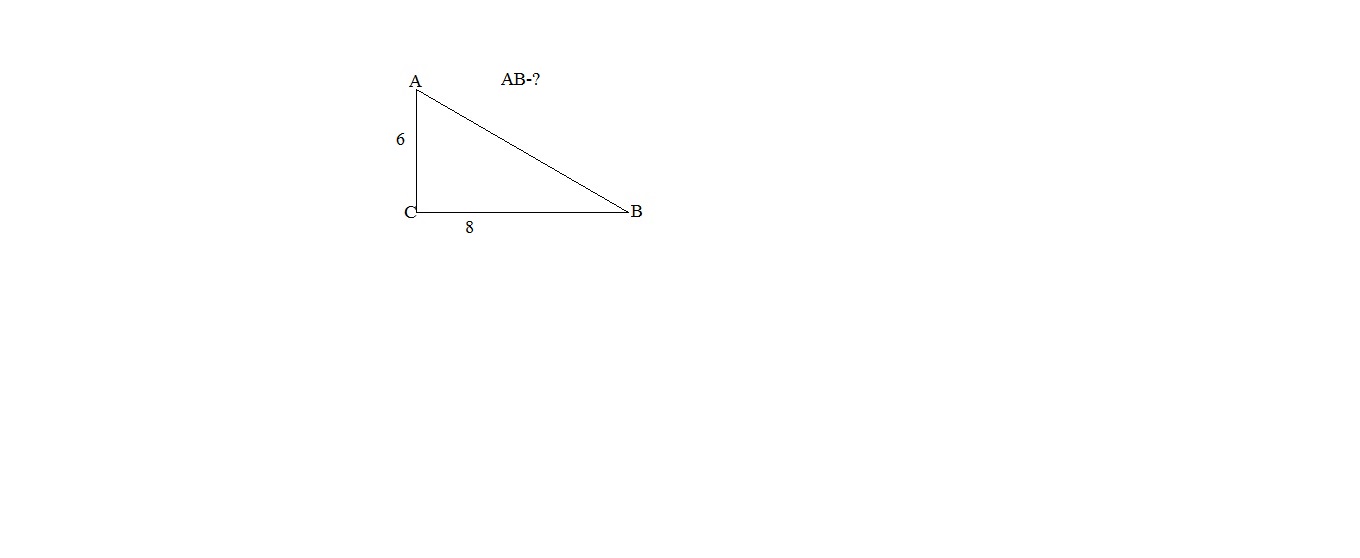
-
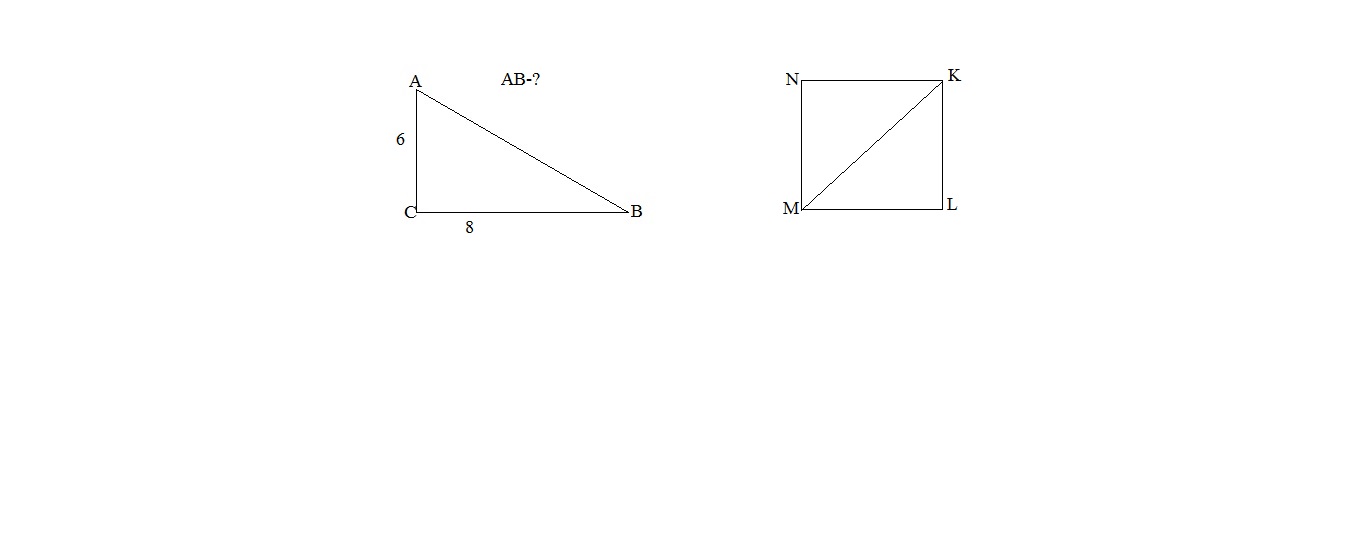 MNKL- квадрат.
PMNKL= 4. MK -?.
MNKL- квадрат.
PMNKL= 4. MK -?.
-
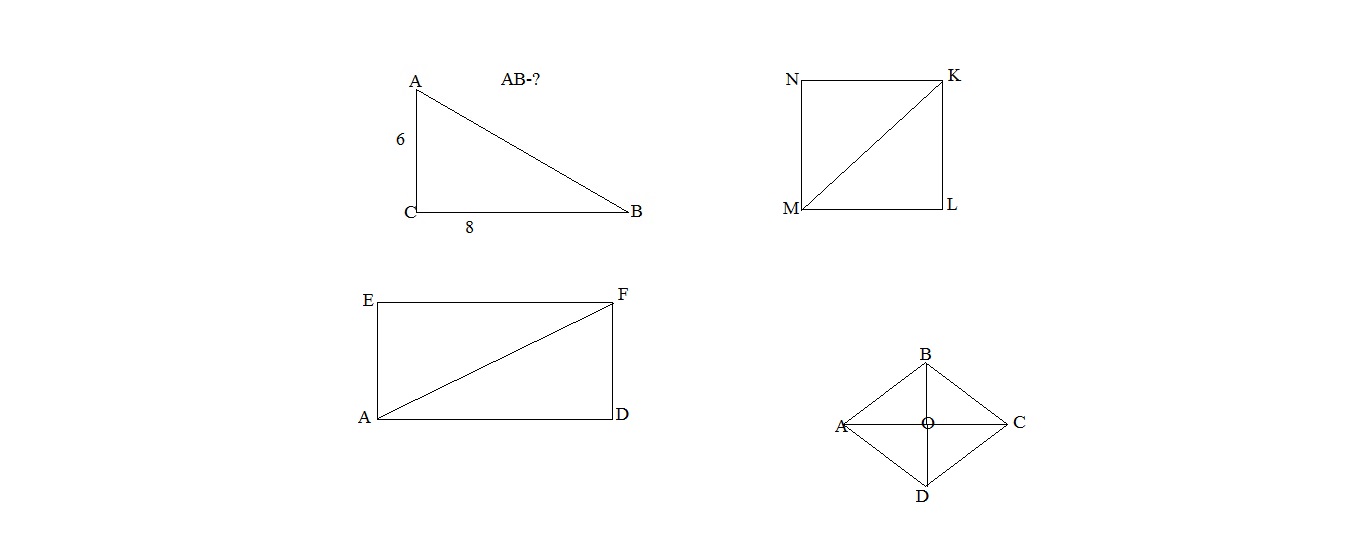 ABCD-ромб. АС=24 см;
BD=18 см. АВ-?
ABCD-ромб. АС=24 см;
BD=18 см. АВ-?
-
 AEFD-прямоугольник. AE=3;
EF=4. AF-?.
AEFD-прямоугольник. AE=3;
EF=4. AF-?.
-
Определить вид треугольника, стороны которого равны 8 см, 15 см, 17 см.(8, 15, 17- пифагорова тройка чисел).
IV Задачи по рисункам (письменно, раздаются карточки)
Решение задач подробно разбирается у доски.
-
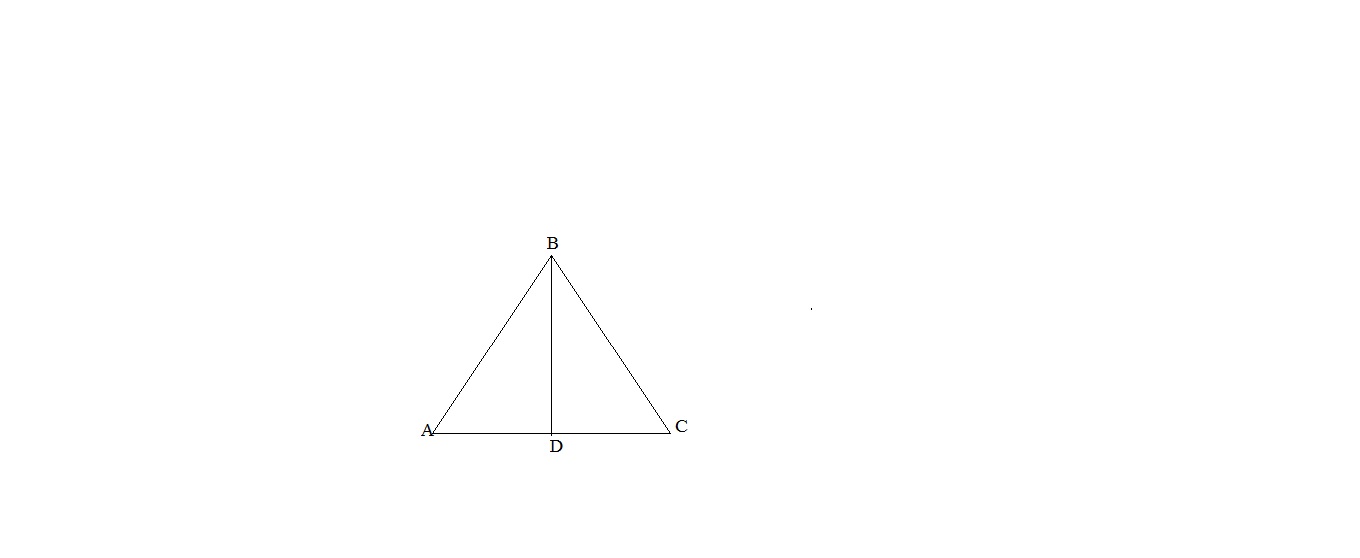 ▲АВС:АВ=ВС=АС.
BD-высота,BD=3дм. АВ-?
▲АВС:АВ=ВС=АС.
BD-высота,BD=3дм. АВ-?
-
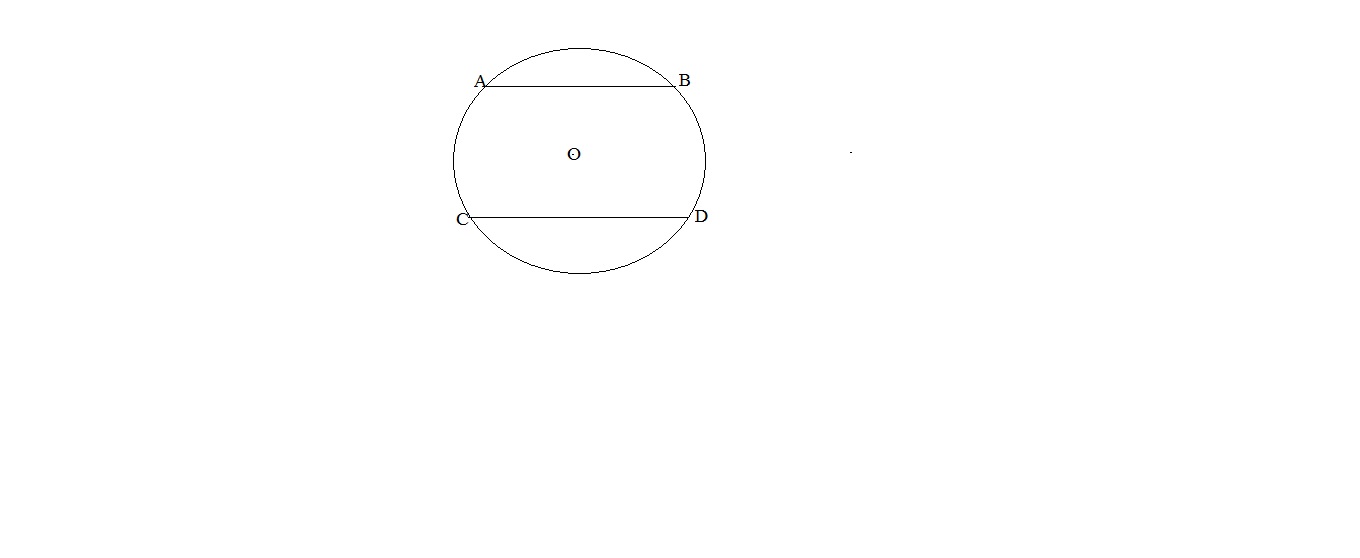 окр.( О,R)
окр.( О,R)
R=25см, АВ и СD-хорды, АВ||CD; AB=30см, CD= 40 см. Найти расстояние между хордами.
V Самостоятельная работа
Вариант 1
-
У прямоугольного треугольника заданы катеты а и в. Найдите гипотенузу, если а=2, в=3.
-
Стороны прямоугольника равны 8 см и 15 см. Чему равна диагональ?
Вариант 2.
-
Найдите периметр прямоугольника, одна сторона которого равна 9 см, а диагональ 15 см.
-
Высота равнобедренного треугольника равна 20 см, а его основание 30 см. Найдите боковую сторону треугольника.
Вариант 3.
-
Стороны прямоугольника 8 и 15 см. Найдите его диагональ.
-
В равнобокой трапеции основания равны 8 см и 14 см, боковая сторона 5 см. Найдите высоту трапеции.
Подведение итогов.
Домашнее задание: подготовить историческую справку о методах доказательства теоремы Пифагора.