- Учителю
- Разработка урока по теме Вычитание векторов. Решение задач.
Разработка урока по теме Вычитание векторов. Решение задач.
Г- 9 класс Урок № 5
Тема: «Вычитание векторов»
Цели урока:
-
Дидактическая: ввести понятие разности двух векторов, рассмотреть теорему о разности векторов; сформировать умение находить разность двух векторов двумя способами.
-
Развивающая: развивать воображение - репродуктивное, творческое, образное; абстрактное и логическое мышление, умение обобщать.
-
Воспитательная: нравственное воздействие, воспитание культуры умственного труда, культуры общения.
Обучающиеся должны:
Знать, какой вектор является разностью двух векторов, теорему о разности векторов.
Уметь строить разность двух векторов двумя способами, применять эти знания при решении задач.
Оборудование: проектор, презентация «Вектора».
Ход урока.
-
Организационный момент.
Сообщение темы и целей урока.
-
Актуализация знаний и умений обучающихся.
-
Проверка выполнения домашнего задания. Разбор нерешенных заданий.
-
Проверка пройденного материала.
-
Тестирование:
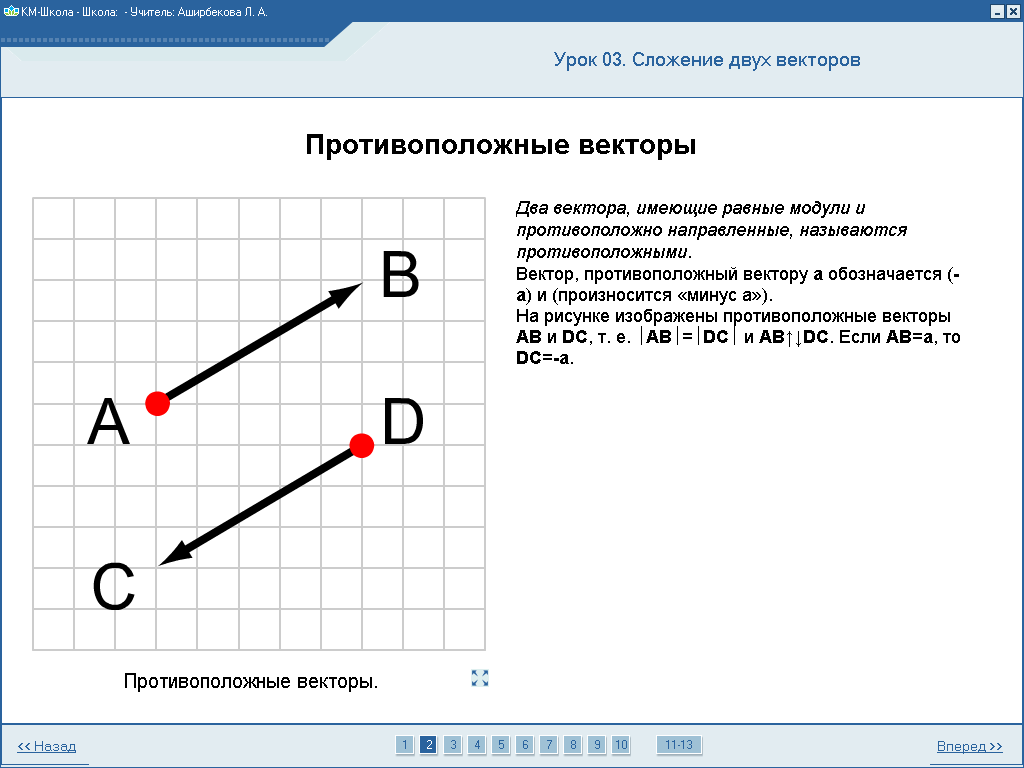
1. Как называются векторы, имеющие равные модули и противоположно направленные?
А) противоположные
Б) противоположно направленные
В) равные
2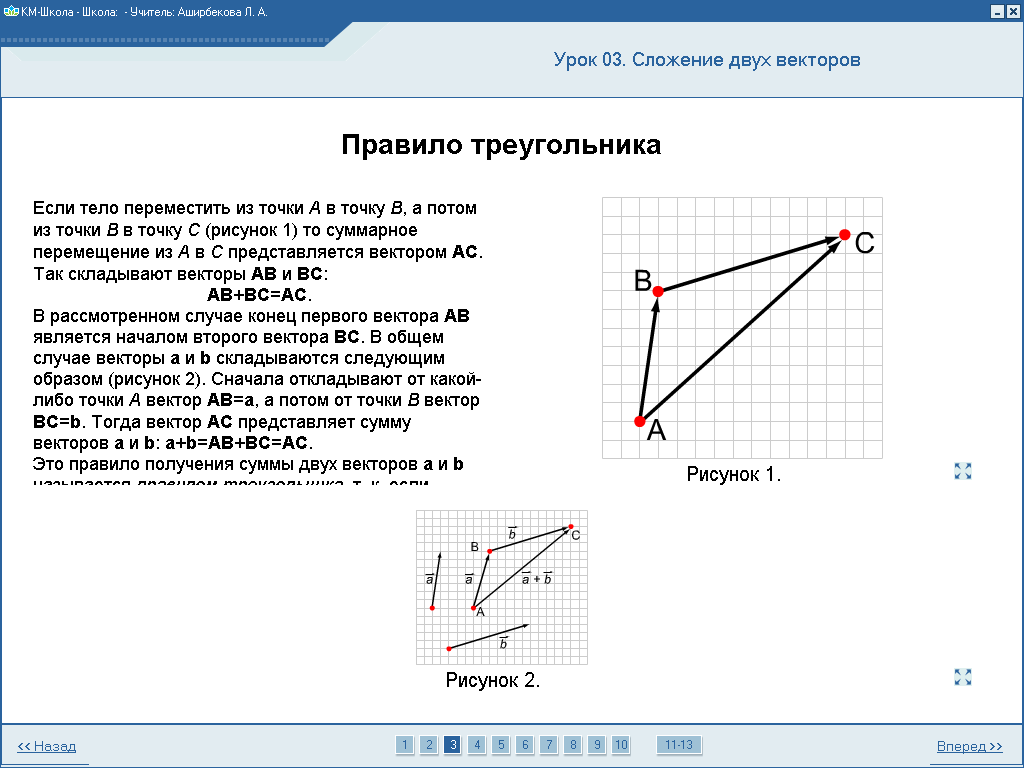
.
Тело переместили из точки А в точку В, а потом из точки В в точку
С. Какой вектор представляет суммарное перемещение тела?
А) 
Б) 
В) 
3. Закончите предложение:
Суммой двух векторов называется вектор, построенный по правилу.... (треугольника)
4. Вставьте пропущенное слово:
Чтобы сложить два неколлинеарных вектора 
и
,
нужно отложить от произвольной точки О векторы 
= и
= и
построить .... ОАСВ, тогда 
=+
(параллелограмм)
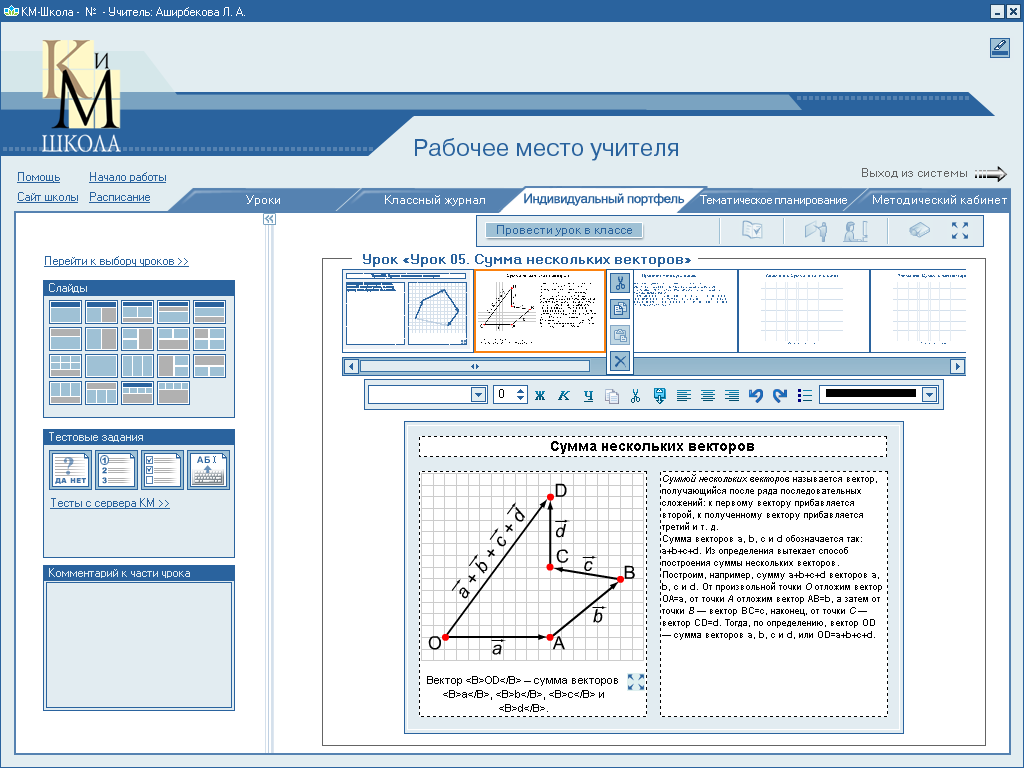5.
Изображенный на рисунке способ построения суммы нескольких векторов
называется правилом...
(многоугольника)
III. Объяснение нового материала:
План объяснения:
1. Разность векторов
В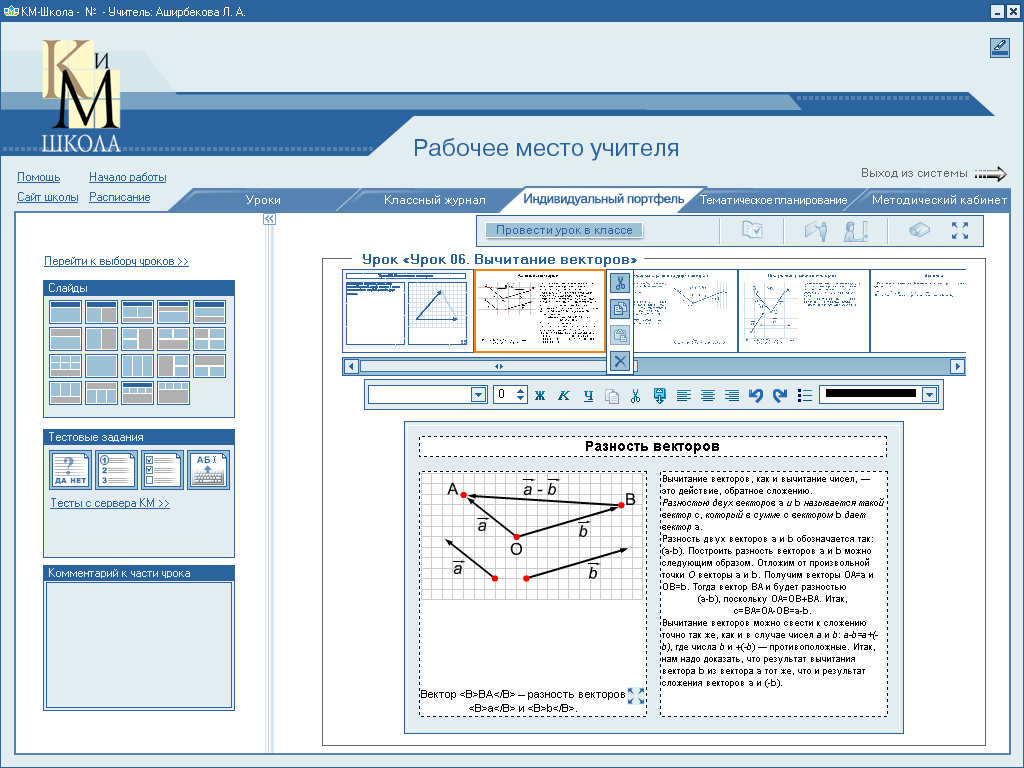
ычитание
векторов, как и вычитание чисел, - это действие, обратное сложению.
Разность двух векторов и
называется такой вектор 
,
который в сумме с вектором дает
вектор .
Разность векторов и
обозначается так: -
.
Построить разность векторов и
можно следующим образом. Отложим от произвольной точки О векторы
и
.
Получим векторы = и
=.
Тогда вектор 
и
будет разностью -
,
поскольку
=+.
Итак,
== -
=
-
.
Вычитание векторов можно свести к сложению точно так же, как и в случае чисел а и b:
а - b = а + (- b), где числа b и + (- b) - противоположные.
Итак, нам надо доказать, что результат вычитания вектора
из
вектора тот
же, что и результат сложения векторов а + (- b).
2. Теорема о разности двух векторов.
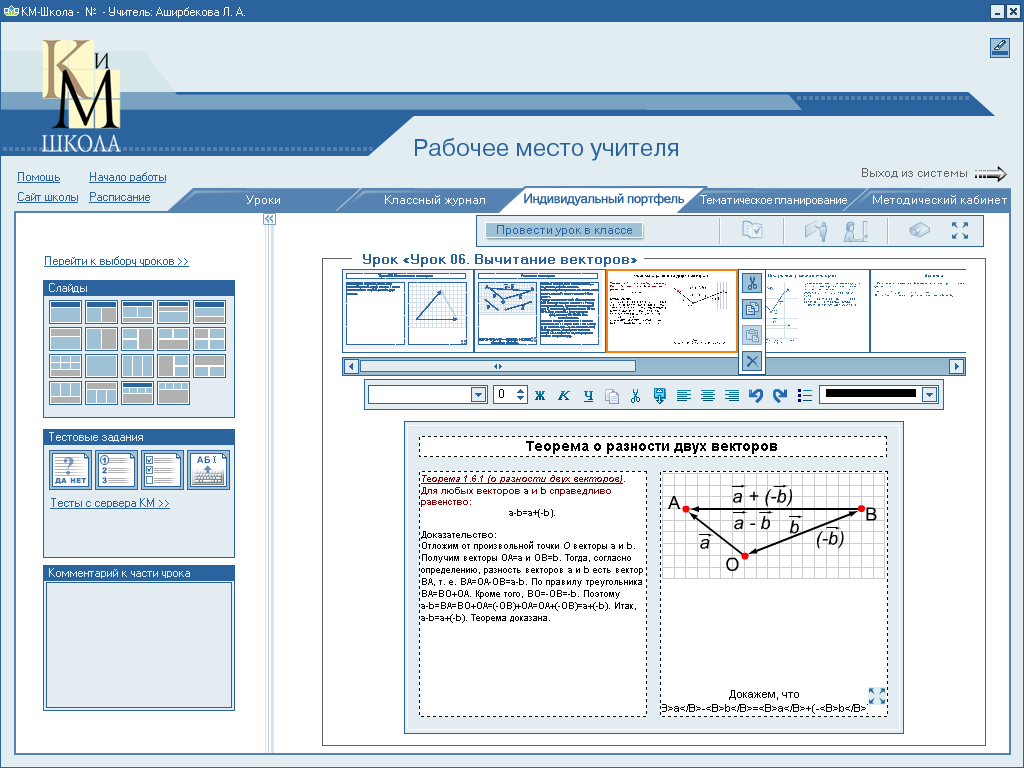
Теорема (о разности векторов)
Для любых векторов и
справедливо равенство -
=
+ (-
).
Доказательство:
Отложим от произвольной точки О векторы и
.
Получим векторы = и
=.
Тогда, согласно определению, разность векторов и
есть
вектор ,
т.е. =
- =
-
. По
правилу треугольника
=
+
.
Кроме того, =
- =
-.
Поэтому -
=
= +
=
(-) +
=+(-)=+(-).
Теорема доказана.
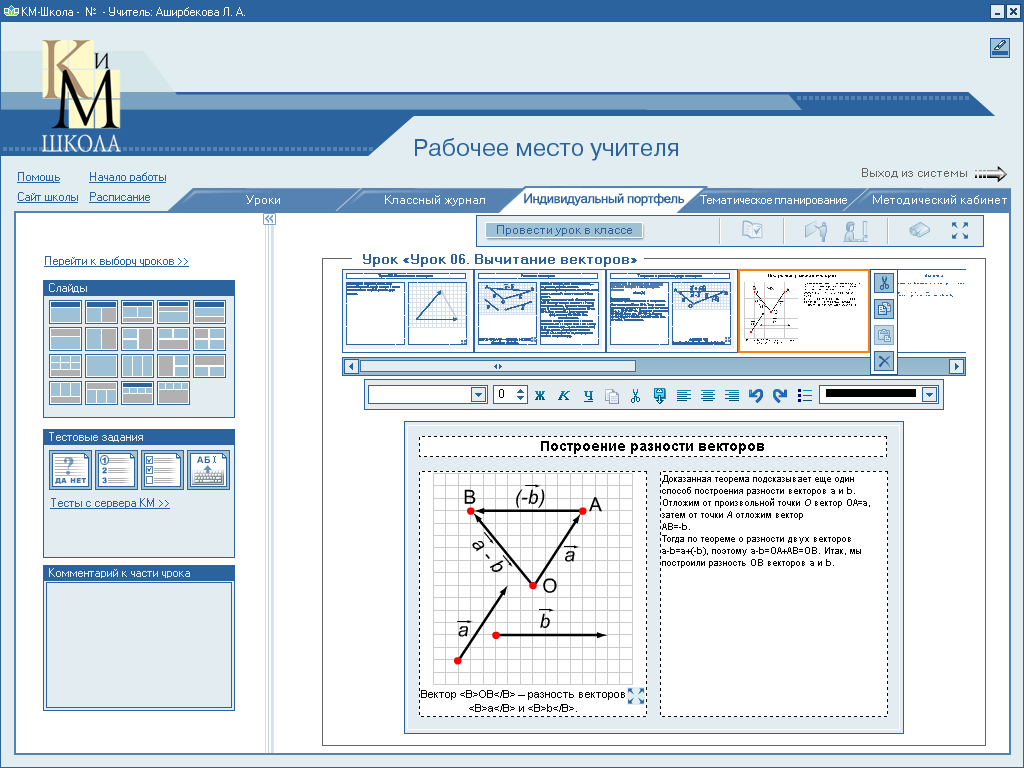
3. Построение разности векторов.
Доказанная теорема подсказывает еще один способ построения
разности векторов и
.
Отложим от произвольной точки О вектор =
,
затем от точки А отложим вектор 
=
-.
Тогда по теореме о разности двух векторов -
= +
(-),
поэтому -
=
+ =
.
Итак, мы построили разность
векторов и
.
IV. Закрепление полученных знаний.
Тестирование.
1. Какой вектор называется разностью векторов и
?
А) Разностью двух векторов и
называется такой вектор 
,
построенный по правилу треугольника.
Б)
Разностью двух векторов и
называется такой вектор ,
который получается после ряда последовательных сложений
В) Разностью двух векторов
и
называется такой вектор ,
который в сумме с вектором дает
вектор
2.
Какой вектор, изображенный на рисунке, является разностью векторов
и ?
А)
Б)
В)
3. №767. Дан треугольник АВС. Выразите векторы
= и
=
вектор 
.
а)
-
б)
-
в) +
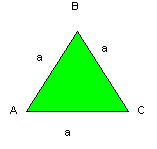
4. №762. Сторона равностороннего треугольника АВС равна а
.Модуль
- = а
да нет
V. Подведение итогов.
Выводы по уроку:
1. Разностью двух векторов и
называется такой вектор ,
который в сумме с вектором дает
вектор .
2. Теорема ( о разности двух векторов): Для любых векторов
и
справедливо равенство:
-
= +
(-).
VI. Домашнее задание: прочитать п.82, решить №№754, 756, 767.
7